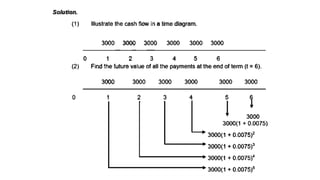
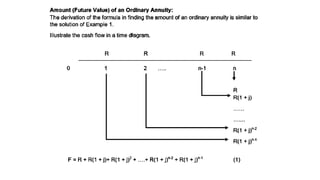
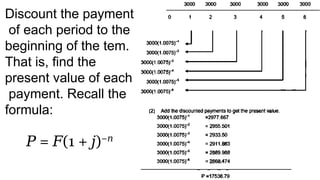
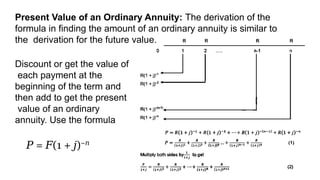
The document explains various types of annuities, including simple, ordinary, due, certain, and contingent annuities, along with definitions of key variables such as term, periodic payment, future value, and present value. It provides examples, particularly focusing on a scenario involving monthly deposits with a specified interest rate and the calculation of both future and present values. Additionally, it outlines the formulas used for determining the future and present values of ordinary annuities.

1. Simple Annuities

2. ANNUITY– a sequence of
payments made at equal(fixed)
intervals or periods of time

3. According to payment interval and
interest period
•Simple Annuity- an annuity where the
payment interval is the same as the interest
period
•General Annuity - an annuity where the
payment interval is not the same as the
interest period

4. According to time of payment
•Ordinary Annuity (or Annuity Immediate)
– a type of annuity in which the payments
are made at the end of each payment
interval
•Annuity Due – a type of annuity in which
the payments are made at beginning of each
payment interval

5. According to duration
•Annuity Certain– an annuity in which
payments begin and end at definite times
•Contingent Annuity – an annuity in which
the payments extend over an indefinite
(or indeterminate) length of time

6. Definition of Variables
• Term of an annuity, t – time between the first
payment interval and last payment interval
• Regular or Periodic payment, R – the amount of each
payment
• Amount (Future Value) of an annuity, F – sum of
future values of all the payments to be made during the
entire term of the annuity
• Present value of an annuity, P – sum of present
values of all the payments to be made during the entire
term of the annuity

7. Time diagram for an ordinary annuity

8. Example 1. Suppose Mrs. Remoto would like
to save P3,000 every month in a fund that
gives 9% compounded monthly. How much is
the amount or future value of her savings
after 6 months?
Given: periodic payment R = P3,000
term t = 6 months
interest rate per annum i(12)
= 0.09
number of conversions per year m = 12
interest rate per period j = 0.09/12 = 0.0075
Find: amount (future value) at the end of the term, F

14. Example 1. Suppose Mrs. Remoto would like
to save P3,000 every month in a fund that
gives 9% compounded monthly. How much is
the amount or future value of her savings
after 6 months?
Given: periodic payment R = P3,000
term t = 6 months
interest rate per annum i(12)
= 0.09
number of conversions per year m =
12
total number of conversions n=(12)(0.5)=6
interest rate per period j = 0.09/12 =
0.0075
Find: amount (future value) at the end of the term, F

15. Given: periodic payment R = P3,000
term t = 6 months
interest rate per annum i(12)
= 0.09
number of conversions per year m =
12
total number of conversions n=(12)(0.5)=6
interest rate per period j = 0.09/12 =
0.0075
amount (future value) at the end of the term, F
Find:
𝐹 = 𝑅
(1 + )
𝑗 𝑛
−1
𝑗
𝐹 = (3000)
(1 + 0.0075)6
−1
0.007
5
𝐹 =
𝑃18,340.89

16. (Recall the problem in Example 1.) Suppose Mrs.
Remoto would like to know the present value of
her monthly deposit of P3,000 when interest is
9% compounded monthly. How much is the
present value of her savings at the end of 6
months?
Given: periodic payment R = P3,000
term t = 6 months
interest rate per annum i(12)
= 0.09
number of conversions per year m =
12
total number of conversions n=(12)(0.5)=6
interest rate per period j = 0.09/12 =
0.0075
Find: present value, P

17. 𝑃 = (1 + )
𝐹 𝑗 −𝑛
Discount the payment
of each period to the
beginning of the tem.
That is, find the
present value of each
payment. Recall the
formula:

18. Present Value of an Ordinary Annuity: The derivation of the
formula in finding the amount of an ordinary annuity is similar to
the derivation for the future value.
Discount or get the value of
each payment at the
beginning of the term and
then add to get the present
value of an ordinary
annuity. Use the formula
𝑃 = (1 + )
𝐹 𝑗 −𝑛

25. 𝐹 = 𝑅
(1 + )
𝑗 𝑛
−1
𝑗
𝐹
𝑅 =
(1 + )
𝑗 𝑛
−1
𝑗
𝐹𝑗
𝑅 =
(1 + )
𝑗 𝑛
−1
𝑃 = 𝑅
1 − 1
+ 𝑗
−𝑛
𝑗
𝑃
𝑅 =
1 − (1 + )
𝑗 −𝑛
𝑗
𝑃𝑗
𝑅 =
1 − (1 + )
𝑗 −𝑛

28. 𝐹 = 𝑅
(1 + )
𝑗 𝑛
−1
𝑗
𝐹𝑗
𝑅 =
(1 + )
𝑗 𝑛
−1
1 − 1
+ 𝑗
−𝑛
𝑗
𝑃𝑗
𝑅 =
1 − (1 + )
𝑗 −𝑛
Future value, F
Present value, P =
𝑃 𝑅
Periodic Payments, R
SIMPLE ANNUITIES