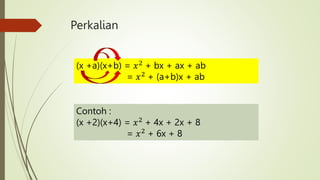
Dokumen ini menjelaskan tentang bentuk aljabar, yang merupakan bentuk matematika yang menggunakan huruf untuk mewakili bilangan yang belum diketahui. Bentuk aljabar terdiri dari suku, koefisien, dan variabel. Suku dapat disebut sejenis jika memiliki variabel yang sama. Operasi penjumlahan dan pengurangan hanya dapat dilakukan pada suku sejenis. Perkalian dan pembagian pada bentuk aljabar juga dijelask

1. ALJABAR

2. Mengenal Bentuk Aljabar

3. PENGERTIAN
Bentuk aljabar adalah suatu bentuk matematika yang
dalam penyajiannya memuat huruf-huruf untuk
mewakili bilangan yang belum diketahui.
Contoh :
3x + 5
Koefisien =
Variabel =
Konstanta =
3
x
5

4. Suku adalah bentuk aljabar yang
dipisahkan oleh tanda penjumlahan atau
pengurangan
2x
3y – 4
5x + 3y -10
satu suku
tiga suku
dua suku

5. Suku Sejenis = suku dengan variabel sama
3x dan 4x
4a dan 5b
𝑦2
𝑑𝑎𝑛 7𝑦
𝑐2
dan 3𝑐2
suku sejenis
suku tidak sejenis
suku tidak sejenis
suku sejenis

6. Penjumlahan dan pengurangan pada bentuk
aljabar hanya dapat dilakukan pada suku yang
sejenis
2a + 4a = 6a
8b – 4b = 4b
5x + 4y – 7 x = -2x + 4y = 4y – 2x
3c – (4d – 2c) = 3c – 4d – (-2c) = 3c – 4d + 2c = 5c – 4d

7. Ingat
𝒂𝒎
x 𝒂𝒏
= 𝒂𝒎+𝒏
𝒂
𝒎
: 𝒂𝒏 = 𝒂𝒎−𝒏
(𝒂𝒎
)𝒏
= 𝒂𝒎 𝒙 𝒏
𝟐𝟑 x 𝟐𝟒 = 𝟐𝟑+𝟒 = 𝟐𝟕
𝟐𝟓
: 𝟐𝟒 = 𝟐𝟓−𝟒 = 𝟐𝟏 = 2
(𝟐𝟐 )𝟑 = 𝟐𝟐 𝒙 𝟑 = 𝟐𝟔

8. Perkalian
a(x) = ax
Contoh :
2 (3x) = 6x -3 (4b) = … -12b
a(x+b) = ax + ab
Contoh :
2 (3x + 5) = 6x + 10 5 (4a - 3) = … 20a - 15

9. Perkalian
(x +a)(x+b) = 𝑥2 + bx + ax + ab
= 𝑥2 + (a+b)x + ab
Contoh :
(x +2)(x+4) = 𝑥2 + 4x + 2x + 8
= 𝑥2 + 6x + 8