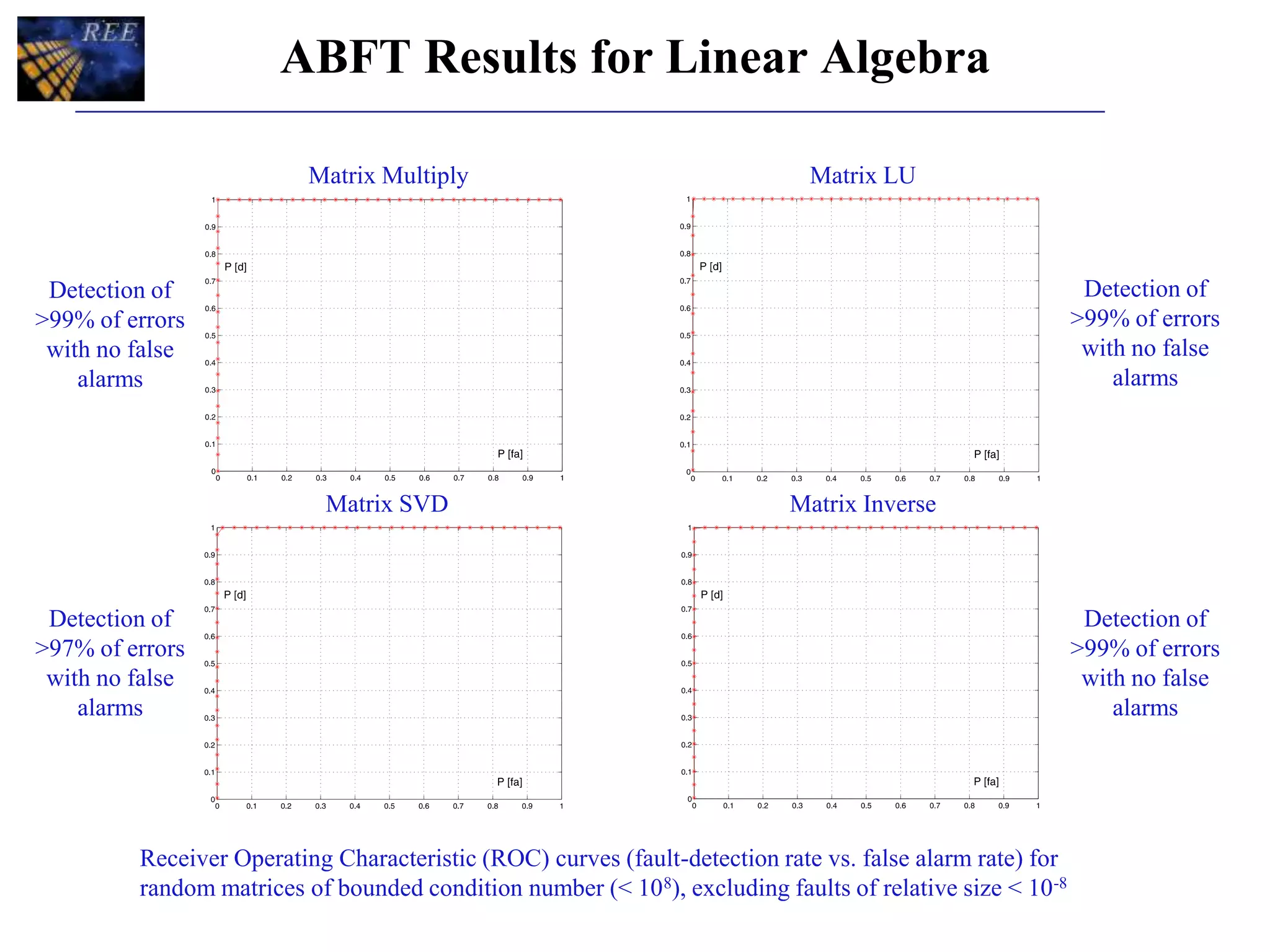
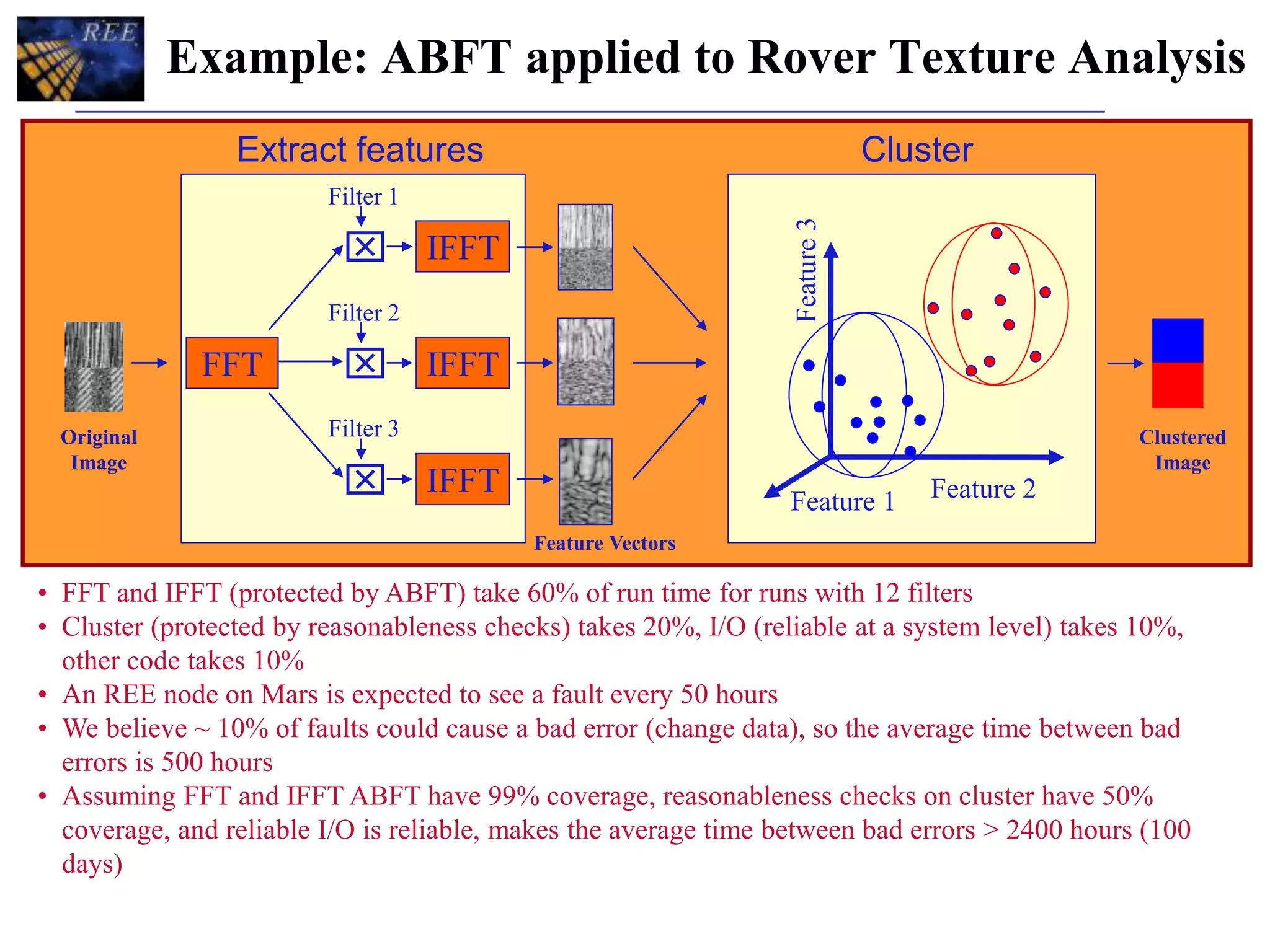
The document discusses application fault tolerance (AFT) strategies for using non-radiation-hardened processors in onboard processing systems to handle errors and faults. It emphasizes the importance of periodic error reporting, state checkpointing, and algorithm-based fault tolerance (ABFT) techniques to safeguard against errors in critical computations like matrix multiplications and fast Fourier transform (FFT). Additionally, it covers application layer fault tolerance and detection (ALFTD) principles, which enable physical nodes to manage fault detection while maintaining acceptable performance levels.

1. Application Fault Tolerance (AFT)
Daniel S. Katz
Former REE Applications Project Element Manager
Jet Propulsion Laboratory
May 2001

2. Fault Tolerance
As previously mentioned, one contribution of REE is to enable use of
non-radiation-hardened processors for on-board processing.
Using the processors, faults will occur
• The fault rate has been predicted
Some of these faults will cause errors
• The error rate has been predicted
We need to tolerate the errors caused by these faults
We examined two types of fault tolerance
• Application Fault Tolerance
This section of the review
• System Fault Tolerance
Covered elsewhere

3. Application Fault Tolerance
Assume a simple executive controlling an application running on
non-rad-hard processors
• The control process must watch the application to ensure it is still
running and not in an infinite loop
• The application then needs to detect errors, and if possible to recover
from them, otherwise to fail so that the control process can restart the
application
• If the total run time of an app (or a frame) is large compared with the
expected fault period, the application should save its state occasionally
This makes the effective run time smaller
Assume that transient faults caused by single event effects are all
that must be handled
• If the application is rerun, the fault will not recur
• Permanent faults handled elsewhere

4. Faults and Errors
Faults cause errors
• Good Errors
Cause the node to crash
Cause the application to crash
Cause the application to hang
Cause the application to go into an infinite loop
– Applications must help detect these errors
• Bad Errors
Change application data
– Application may complete, but the output may be wrong
– Only the applications can detect these errors without replication
– Using Algorithm-Based Fault Tolerance (ABFT), ALFTD, assertion
checking, other techniques

5. Detecting and Handling Good Errors
1. Applications must periodically report that they are making
progress
• We have defined a smart heartbeat API
Really, more of a deadman timer
Example: every 5 seconds, the application must report a value which is larger
than the previously reported value
Application programmer is responsible for ensuring that an infinite loop
cannot fool this mechanism, possibly with a second timer around the loop.
2. Applications also must report successful completion
If either fails, the control process must restart the application

6. Application Restarts
If the time between faults is short compared with the run time of the
application, the application may never complete because of restarts
We use checkpointing to save the state of the application
When the application is restarted, it can reload this state (or, if the
data is time critical, it can restart from scratch with new data)
We have defined an API for application-controlled checkpointing
• Ensures only important data is saved; not temporaries

7. Detecting Bad Errors
First step is good programming
We have defined a set of rules for application programmers
• Examples:
Examine return codes from subroutine calls
– Does MPI_Send() return 0?
– Does malloc() return 0?
Sanity/Reasonableness checks
– Output of clustering into 3 textures should be integers from 1 to 3
– No single pixel should be a region
• Most of these ideas are used by developers, but then turned off after the
code has been checked out
• They need to be kept
Basic rule if error is detected: call exit and let the control program
restart the application

8. Detecting Bad Error using
Algorithm-Based Fault Tolerance (ABFT)
ABFT started in 1984 with Huang and Abraham
• Theory for ABFT techniques exist for many common linear numerical
algorithms, such as
Matrix multiply, LU decomposition, QR decomposition, single value
decomposition (SVD), fast Fourier transform (FFT)
• Require an error tolerance
Setting of this error tolerance involves a trade-off between missing errors and
false positives because of computational round-off
• The key reason why ABFT works is that the additional work that must be
done to check these operations is of lower order that the operations
themselves
Check of matrix-matrix multiple is O(n2), multiply is O(n3)
Check of FFT is O(n), FFT is O(n log n)
This allows these routines to be verified with lower overhead than would be
needed if the calculation was replicated
• These routines are key parts of many REE applications
For example, NGST phase retrieval application spends 70% of its cycles in FFT
If we can detect all errors in FFT, we have reduced the number of errors which
might impact the data by 70%

9. Details of ABFT for Matrix-Matrix Multiply
Algorithm-Based Fault Tolerance (ABFT) - Huang and Abraham (1984):
• Calculate C = A B, where A, B, and C are augmented
• Extra rows are added to A, extra columns are added to C
• The rows added to A are test vectors right multiplied by A
• The columns added to B are test vectors left multiplied by B
• Because matrix-matrix multiplication is a linear operation, it is known how these
rows and columns should be transformed, and when the multiplication of the
augmented matrices is completed, the are checked
• Libraries which use ABFT must either copy data to larger arrays or demand
larger arrays be used outside
Result checking (RC) - Wasserman and Blum (1997), Prata and Silva (1999),
Turmon et al. (2000), Gunnels et al. (2001):
• Check C w = A (B w) as a post condition
• Initial arrays are not changed
• Library can be written as a black box, with same used interface as non-RC library
• REE sponsored work of Turmon et al., which studied error tolerance with respect
to numerical round-off error, focusing on fairly well-conditioned matrices
(condition number < 1x108)
• REE sponsored work of Gunnels et al., which studied the properties of right- and
left-sided multiplication of test vectors, and created a methodology for achieving
low-overhead error recovery in a high performance library

10. REE ABFT Work
REE built ABFT versions of matrix-matrix multiply, LU decomposition,
matrix inverse, and SVD routines of ScaLAPACK library
• ScaLAPACK is the most popular parallel linear algebra library
• To the best of our knowledge, this is the first wrapping of a general
purpose parallel library with an ABFT shell
• Interface the same as standard ScaLAPACK with the addition of an extra
error return code
REE built ABFT version of high performance matrix-matrix multiply,
which is integrated as kernel of all BLAS3 routines
• BLAS routines are single processor linear algebra libraries used as
building blocks for parallel libraries, and by users
• BLAS3 routines are matrix-matrix routines (as opposed to vector routines -
BLAS1 and vector-matrix routines - BLAS2)
REE built ABFT version of FFTW
• FFTW is the most popular single-processor and parallel FFT package
• Interface the same as standard FFTW with the addition of an extra error
return code

11. ABFT Results for Linear Algebra
Receiver Operating Characteristic (ROC) curves (fault-detection rate vs. false alarm rate) for
random matrices of bounded condition number (< 108), excluding faults of relative size < 10-8
Matrix Multiply
Matrix SVD
Matrix LU
Matrix Inverse
Detection of
>99% of errors
with no false
alarms
Detection of
>99% of errors
with no false
alarms
Detection of
>99% of errors
with no false
alarms
Detection of
>97% of errors
with no false
alarms

12. ABFT Results for FFT

13. On a 650 MHz Pentium III:
Overhead of Error Detection and Correction
on Matrix-Matrix Multiplication
0 100 200 300 400 500
0
20
40
60
80
100
Matrix size (m=n=k)
percentofpeak
Multiply
Detect (0 errors)
Correct (1 error)
0
130
260
390
520
650
MFLOPS/sec

14. Example: ABFT applied to Rover Texture Analysis
Extract features Cluster
Feature 1
Feature3
Feature 2
Clustered
Image
Feature Vectors
IFFTx
IFFTx
Original
Image
Filter 2
Filter 1
Filter 3
IFFTx
FFT
• FFT and IFFT (protected by ABFT) take 60% of run time for runs with 12 filters
• Cluster (protected by reasonableness checks) takes 20%, I/O (reliable at a system level) takes 10%,
other code takes 10%
• An REE node on Mars is expected to see a fault every 50 hours
• We believe ~ 10% of faults could cause a bad error (change data), so the average time between bad
errors is 500 hours
• Assuming FFT and IFFT ABFT have 99% coverage, reasonableness checks on cluster have 50%
coverage, and reliable I/O is reliable, makes the average time between bad errors > 2400 hours (100
days)

15. ALFTD Fault Tolerance
Application Layer Fault Tolerance and Detection, developed by Prof.
Israel Koren et al., U. Mass
ALFTD fault tolerance principles:
• Every physical node will run its own work (primary) as well as a scaled
down copy of a neighboring node’s work (secondary)
• If a fault should corrupt a process, the corresponding secondary of that
task will still produce output, albeit at a lower quality
ALFTD fault tolerance is tunable
• It permits users to trade off amount of fault tolerance against
computation overhead
(How scaled down should the secondary be?)
• Allowing more overhead for ALFTD computation produces better results
• The secondary can be run optionally on an as-needed basis;
If the corresponding primary is approaching a deadline miss
If the corresponding primary has been incapacitated
If the corresponding primary has produced faulty data
If faults are infrequent, the secondary will incur very little additional overhead

16. ALFTD Fault Detection
ALFTD tested on OTIS application
OTIS lends itself to ALFTD because output data is “natural”
temperature data of a geographic area. This means the data has
• Local Correlation: The data changes gradually over an area. Sharp
changes can be used as flags for potential faults.
• Absolute Bounds: The data falls within some expected range. Extreme
hot or cold spots can be used as flags for potential faults.
Fault detection filters were created which scan for unexpected data
(perform reasonableness checks)

17. ALFTD Example
Output with no faults injected
No ALFTD 25% ALFTD Computation Overhead
33% ALFTD Computation Overhead 50% ALFTD Computation Overhead
Outputs with faults injected
Temperature
outputs from
sample OTIS run

18. ALFTD Example
ALFTD can provide significant error savings with low computation overhead

19. Routine
ABFT Error
coverage
Parallel Matrix Multiplication >99%
Parallel Matrix Inverse >99%
Parallel LU Decomposition >99%
Parallel SVD >97%
BLAS3 (single processor routines based
on Matrix Multiplication)
>99%
Parallel and single processor FFT >97%
AFT Results
We have developed APIs for applications to communicate with a
control program to ensure good errors are detected and corrected
• API for smart heartbeats
• API for application checkpoint
We have developed a suite of tools
to detect and correct bad errors
• Rules for application developers
• ABFT routines at multiple levels
for linear algebra
• ABFT routines for FFT
• ALFTD reasonableness checks
• ALFTD fault correction examples
Missions can now begin developing applications for on-board
processing using non-rad-hard processors
• The applications can be tested using the REE testbeds and fault injection
tools previously discussed
• The AFT tools can be used to improve the fault response of the
applications to acceptable levels for the mission
• It is very likely, based on initial examples, that science applications can
achieve high reliability on these processors

20. References (1) (compiled after presentation)
• J. Beahan, L. Edmonds, R. Ferraro, A. Johnston, D. S. Katz, and R.
R. Some, "Detailed Radiation Fault Modeling of the Remote
Exploration and Experimentation (REE) First Generation Testbed
Architecture," Proceedings of the IEEE Aerospace Conference,
2000. DOI: 10.1109/AERO.2000.878499
• F. Chen, L. Craymer, J. Deifik, A. J. Fogel, D. S. Katz, A. G. Silliman,
Jr, R. R. Some, S. A. Upchurch, and K. Whisnant, "Demonstration
of the Remote Exploration and Experimentation (REE) Fault-
Tolerant Parallel-Processing Supercomputer for Spacecraft
Onboard Scientific Data Processing," Proceedings of International
Conference on Dependable Systems and Networks, 2000. DOI:
10.1109/ICDSN.2000.857562
• M. Turmon, R. Granat, and D. S. Katz, "Software-Implemented Fault
Detection for High-Performance Space Applications," Proceedings
of International Conference on Dependable Systems and Networks,
2000. DOI: 10.1109/ICDSN.2000.857522
• S. A. Curtis, M. Rilee, M. Bhat, and D. Katz, "Small Satellite
Constellation Autonomy via on-board Supercomputers and
Artificial Intelligence," International Astronautical Federation, 51st
Congress, 2000.

21. References (2) (compiled after presentation)
• R. Sengupta, J. D. Offenberg, D. J. Fixsen, D. S. Katz, P. L.
Springer, H. S. Stockman, M. A. Nieto-Santisteban, R. J. Hanisch,
and J. C. Mather, "Software Fault Tolerance for Low-to-Moderate
Radiation Environments," Proceedings of Astronomical Data
Analysis Software and Systems (ADASS) X, 2000.
• D. S. Katz and P. L. Springer "Development of a Spaceborne
Embedded Cluster," Proceedings of 2000 IEEE International
Conference on Cluster Computing (Cluster 2000), 2000. DOI:
10.1109/CLUSTR.2000.889012
• D. S. Katz, and J. Kepner, "Embedded/Real-Time Systems,"
International Journal of High Performance Computing Applications
(special issue: Cluster Computing White Paper), v. 15(2), pp. 186-
190, Summer 2001. DOI: 10.1177/109434200101500212
• J. A. Gunnels, D. S. Katz, E. S. Quintana-Ortí, and R. A. van de
Geijn, "Fault-Tolerant High-Performance Matrix Multiplication:
Theory and Practice," Proceedings of International Conference on
Dependable Systems and Networks, 2001. DOI:
10.1109/DSN.2001.941390

22. References (3) (compiled after presentation)
• T. Sterling, D. S. Katz, and L. Bergman, "High-Performance
Computing Systems for Autonomous Spaceborne Missions,"
International Journal of High Performance Computing
Applications, v. 15(3), pp. 282-296, Fall 2001. DOI:
10.1177/109434200101500306
• D. S. Katz and R. R. Some, "NASA Advances Robotic Space
Exploration," IEEE Computer, v. 36(1), pp. 52-61, January 2003.
DOI: 10.1109/MC.2003.1160056
• M. Turmon, R. Granat, D. S. Katz, and J. Z. Lou, "Tests and
Tolerances for High-Performance Software-Implemented Fault
Detection," IEEE Transactions on Computers, v.52(5), pp. 579-591,
May 2003. DOI: 10.1109/TC.2003.1197125
• E. Ciocca, I. Koren, Z. Koren, C. M. Krishna, and D. S. Katz,
"Application-Level Fault Tolerance and Detection in the Orbital
Thermal Imaging Spectrometer," Proceedings of the 2004 Pacific
Rim International Symposium on Dependable Computing, pp. 43-
48, 2004. DOI: 10.1109/PRDC.2004.1276551