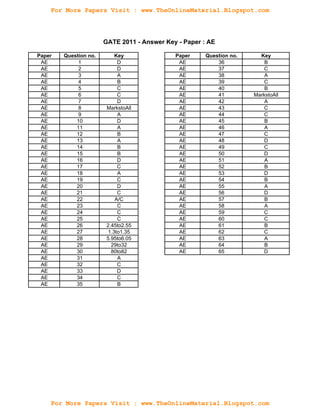
The document provides instructions for an online aerospace engineering examination. It states that the exam has 65 multiple-choice questions worth a total of 100 marks. Questions are either worth 1 or 2 marks depending on the question number. There is no negative marking for numerical answer questions but negative marking for multiple choice questions. Calculators are allowed but no other materials. The exam is timed for 3 hours.