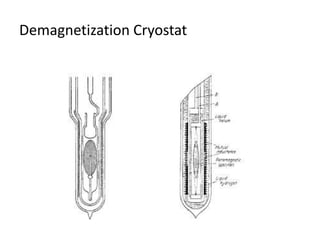
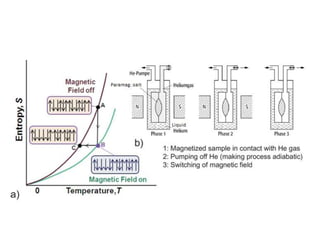
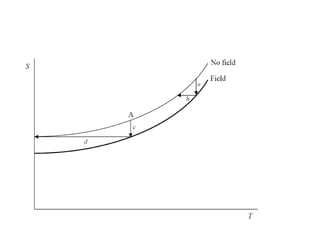
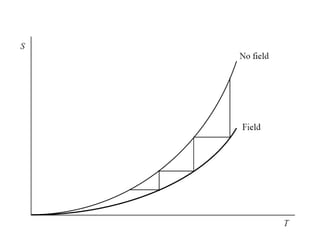
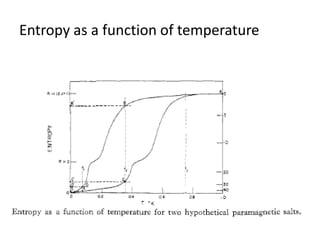
1) Adiabatic demagnetization is a technique for producing low temperatures by magnetizing and demagnetizing paramagnetic salts. 2) Langevin's theory from 1905 explained that magnetizing paramagnetic substances results in heating, while demagnetizing results in cooling due to reversible temperature changes. 3) The first successful experiments using this technique were carried out in 1933 by Giaque and MacDougall using gadolinium sulfate, achieving temperatures as low as 0.53 K and 0.23 K through magnetization and demagnetization respectively.

1. ADIABATIC DEMAGNETIZATION
OF
PARAMAGENETIC SALTS
ATHUL RAJ T K
Mechanical Engineering

2. History
• Langevin (1905) pointed out that changes in the
magnetization of paramagnetic substances must be
accompanied by reversible temperature changes.
• Debye (1926) and Giaque (1927) suggested independently
reversible temperature effects connected with the
magnetization of certain paramagnetic salts might be used for
producing temperatures well below the BP of Helium
• First experiments were carried out in 1933 by Giaque and
MacDougall and since then magnetic cooling has become an
established cryogenic technique.

3. Langevin’s Theory
• An assembly of non-interacting magnetic dipoles, in the
absence of external magnetic field are randomly oriented.
• Upon application of magnetic field, B the energy of a given
dipole depends on its orientation w.r.t the field direction.
• Magnetic moment, M depend only on the ratio B/T
• If pressure and volume effects are neglected, enthalpy
)
/
( 3
Tm
Nm
volume
unit
per
moment
Dipole
M
MdB
TdS
dH
BM
U
H






7. Remarks
• If is negative isentropic magnetization will be
accompanied by heating and demagnetization by cooling.
• Energy of magnetization appears in the form of heat.
• The effect is small at ordinary temperatures where is
small and the heat capacity is large.
B
T
M
)
(


B
T
M
)
(



8. Historical activities
• Kamerlingh Onnes (1923) discovered that some paramagnetic
salts (eg. Gadolinum sulphate) behaved according to
Langevin’s theory even at the BP of He where specific heat
was small and is appreciable.
• In the first experiment of Giaque and MacDougall, using
Gadolinum sulphate reached 0.53 K starting from 3.4 K and
subsequently 0.23 K demagnetizing from 1.5 K.
• deHaas, Wiersma and Kramers (1933) used Cerium Fluoride
and reached 0.27 K . Better results were obtained by using
Cerium and Dysprosium Ethyl Suplhates and Potassium
Chromic Alum by the same investigators.

9. Entropy as a function of temperature

10. Demagnetization Cryostat