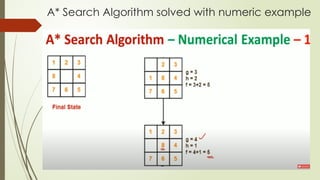
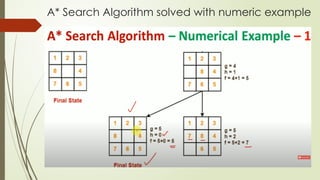
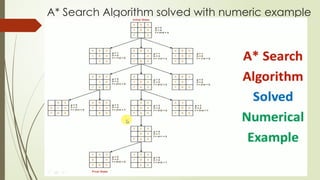
The document discusses the A* search algorithm, detailing the implications of different heuristic functions on its optimality. It explains the conditions under which a heuristic is admissible, consistent, or leads to an overlooked optimum solution. Specific examples illustrate how these heuristics interact with actual costs in search scenarios.

1. A* Search Algorithm
 A* Search Algorithm solved with numeric example

2. A* Search Algorithm solved with numeric example

3. A* Search Algorithm solved with numeric example

4. A* Search Algorithm solved with numeric example

5. A* Search Algorithm solved with numeric example

6. A* Search Algorithm solved with numeric example

7. A* Search Algorithm solved with numeric example

8. A* Search Algorithm solved with numeric example

9. A* Search Algorithm solved with numeric example

10. Heuristic Function h(n) and how to make it

11. Heuristic Function h(n) and how to make it

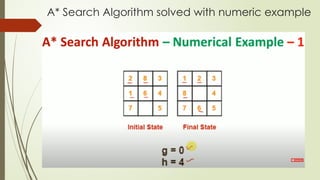
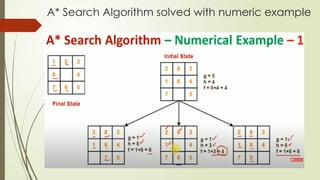
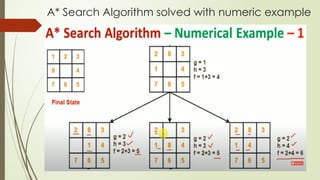
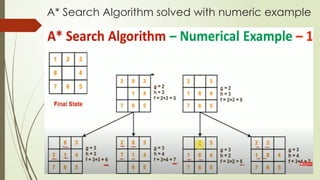
12. Optimality of A* Search Algorithm
 Heuristic may be:
 h(n) > actual cost
 h(n) = actual cost
 h(n) < actual cost
 (1) h(n) > actual cost [Optimum solution can be overlooked, optimum solution is not
possible]
 (2) h(n) = actual cost [Best case scenario, if h(n) approximates actual cost, searching
uses minimum of node to the goal]
 (3) h(n) < actual cost [ Admissible, Consistent Heuristics]

13. Optimality of A* Search Algorithm
h(n) > actual cost [Optimum solution can be overlooked, optimum solution is not
possible]

14. Optimality of A* Search Algorithm
h(n) > actual cost [Optimum solution can be overlooked, optimum solution is not
possible]

15. Optimality of A* Search Algorithm
h(n) > actual cost [Optimum solution can be overlooked, optimum solution is not
possible]
b………….> dest and cost (7+2+0=9) , or ……….>a and cost (2+9=11)

16. Optimality of A* Search Algorithm
h(n) > actual cost [Optimum solution can be overlooked, optimum solution is not
possible]
b………….> dest and cost (7+2+0=9) , or ……….>a and cost (2+9=11)
Actual cost from Sabdest =2+3+2=7
h(n)=10 > actual cost = 7

17. Optimality of A* Search Algorithm
 h(n) < actual cost, if this relation maintains for every node, then we say this
this Admissible Heuristics.

18. Optimality of A* Search Algorithm

19. Optimality of A* Search Algorithm

20. Optimality of A* Search Algorithm

21. Optimality of A* Search Algorithm

22. Optimality of A* Search Algorithm
If Heuristic admissible but not consistent, it may not be provided optimum solution.
For optimum solution, heuristic must be consistent. If it consistent, it must be admissible.

23. Optimality of A* Search Algorithm

24. Random Variable
 The domain