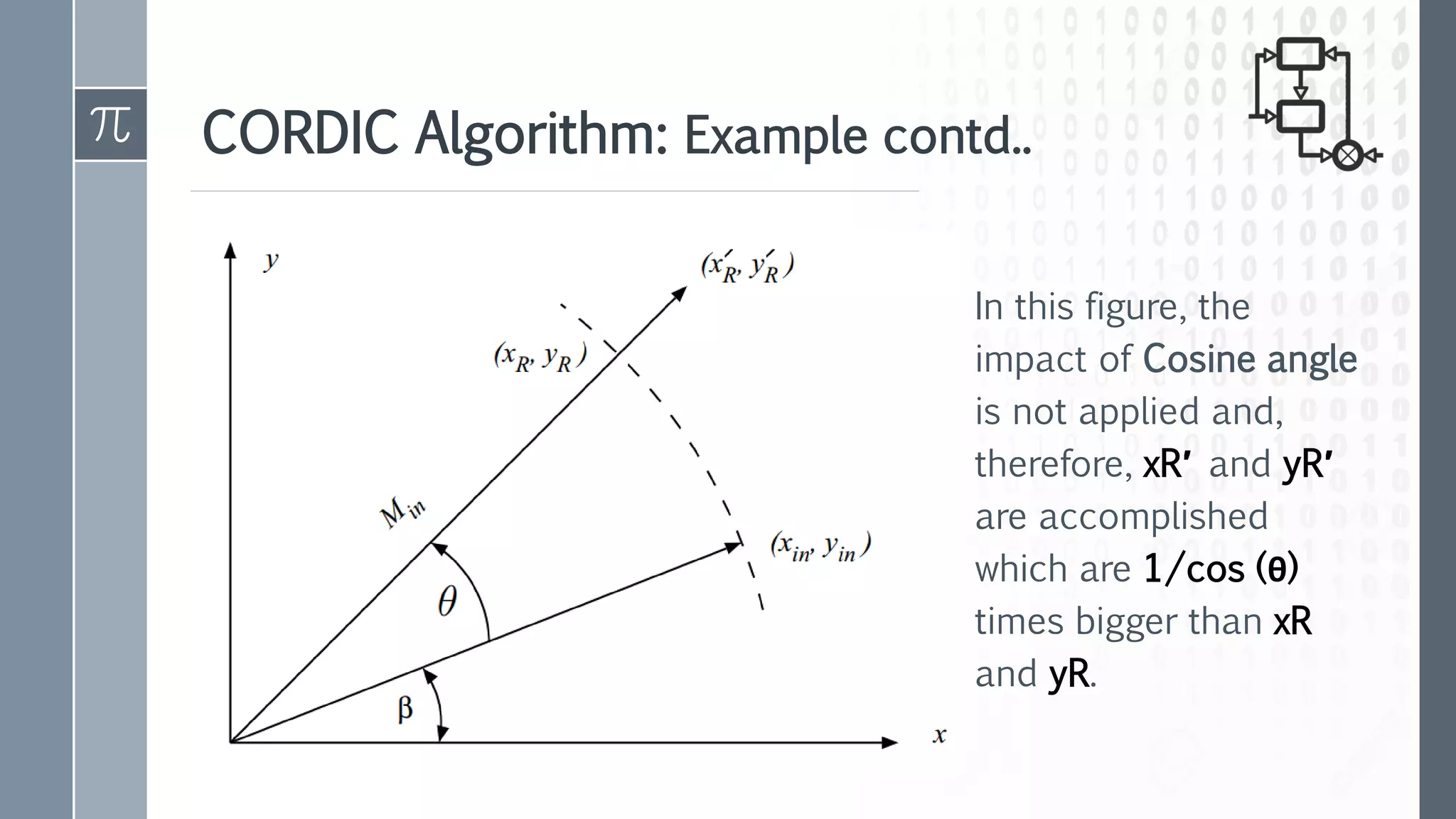
The document summarizes the CORDIC (Coordinate Rotation Digital Computer) algorithm, which is used to calculate trigonometric, exponential, and logarithmic functions using iterative rotation. It explains that CORDIC performs these calculations using small incremental rotations rather than multiplications or divisions. An example is provided to demonstrate how CORDIC uses successive rotations to compute the sine of an angle. The summary concludes that CORDIC obtains ideal rotation results by taking the scaling factor into account without affecting the accuracy of the final calculations.

1. “A Research on How
Calculators operate:
Understand how calculators/computers actually compute
exponentials, logarithms, and trigonometric functions”

2. Introduction
› Calculators use different algorithms to
calculate trigonometric angles,
exponentials and logarithms.
› Coordinate Rotation Digital Computer
(CORDIC) algorithm is one of the most
important algorithms among them.
› This paper describes how the CORDIC
works and gives an approximate
solution for a given angle.
› Also, an example will be used for
better understanding.

3. Example: Trigonometric function
‘Taylor series’ for the sine is used to take an accurate result:
Sin (a) = a – a3/3! + a5/5! − a7/7! + ...,
In this equation, x is measured as radians.
For example, for finding the sine angle of 50, first we convert 50
into radians. We get 50/180 π = 0.872665.
Then use the above formula to get the value of sin 0.872665:
= 0.872665− 0.8726653/3! + 0.8726655/5! − 0.8726657/7!
= 0.872665− 0. 296737492 + 0.000059350 − 0.000000256
= 0.86921155472665

4. CORDIC Algorithm
› CORDIC is an iterative technique which uses to
discover a wide extent of fundamental limits.
› We present a precise and exhaustive scientific
categorization of rotational CORDIC calculations.
› Exceptional consideration has been given to the higher
radix and level strategies proposed in the writing for
diminishing the idleness.
› CORDIC is utilized as a structure hinders in different
single chip arrangements, the basic viewpoints to be
considered are rapid, low force, and low zone, for
accomplishing sensible generally speaking execution.

5. CORDIC Algorithm: Explanation
› Picking the starting point as the point of convergence of rotate, we
will show up at the point (x1, y1) by turning the point (x0, y0) by θ.
𝑦𝑅 = 𝑦𝑖𝑛 cos 𝜃 + 𝑥𝑖𝑛 sin 𝜃
𝑋𝑅 = − 𝑦𝑖𝑛 sin 𝜃 + 𝑋𝑖𝑛 cos 𝜃
Now, Put 𝑦𝑖𝑛 = 0 and 𝑥𝑖𝑛= 1,
after rotation, then the
equation becomes
𝑥𝑅 = cos 𝜃
𝑦𝑅 = sin 𝜃

6. CORDIC Algorithm: Example
𝑥𝑅
𝑦𝑅
= cos 𝜃
1 − tan 𝜃
tan 𝜃 1
𝑥𝑖𝑛
𝑦𝑖𝑛
The above equation shows that for each of the one rotation, we need
to perform 4 augmentations.
› The solicitation that lingering parts is, in what limit may we dodge
these enlargements?
The CORDIC count resorts to two urgent structures to accomplish
turn without an increase. The standard central thought is that
pivoting the information vector by a theoretical point 𝜃𝑑 is equivalent
to turning the vector by a few smaller angles

7. The above equation shows that for
each of the one rotation, we need to
perform 4 augmentations.
CORDIC Algorithm: Example contd..
In this figure, the
impact of Cosine angle
is not applied and,
therefore, xR′ and yR′
are accomplished
which are 1/cos (θ)
times bigger than xR
and yR.

8. The above equation shows that for
each of the one rotation, we need to
perform 4 augmentations.
CORDIC Algorithm: Example contd..
𝑥0
𝑦0
= cos 45°
1 − tan 45
tan 45 1
𝑥𝑖𝑛
𝑦𝑖𝑛
→ (Equation 4)
Now for the second step, the second rotation takes place,
𝑥1
𝑦1
= cos 23.55° 1 −2−1
2−1
1
𝑥0
𝑦0
→ (Equation 5)
Now combining both equation 4 and 5 we get,
𝑥1
𝑦1
= cos(45°) cos(26.55°)
1 − tan 45
tan 45 1
1 −2−1
2−1 1
𝑥𝑖𝑛
𝑦𝑖𝑛
→(Equation 6)

9. The above equation shows that for
each of the one rotation, we need to
perform 4 augmentations.
CORDIC Algorithm: Example contd..
Also, for the 3rd rotation we have,
𝑥2
𝑦2
= cos(−12.012°) 1 2−2
−2−2 1
𝑥1
𝑦1
→ (Equation 7)
Final the equation becomes,
𝑥1
𝑦1
=
cos(23.55°) cos(45°) cos(−12.02°) 1 −2−1
2−1
1
1 − tan 45
tan 45 1
1 2−2
−2−2
1
𝑥𝑖𝑛
𝑦𝑖𝑛
→ (Equation 8)

10. Discussion
› Each turn arranges a scaling factor which shows up in the last checks.
› Some new outcomes that permit quick and simple marked digit
execution of CORDIC, without adjusting the fundamental emphasis step
are given.
› A slight alteration would make it conceivable to utilize a convey spare
portrayal of numbers, rather than a marked digit one.
› The technique, called the spreading CORDIC strategy, comprises of
acting in equal two exemplary CORDIC pivots. It gives a steady
standardization factor.
› Therefore, cos (θ) inclines toward solidarity.
› Thusly, if the check is relied upon to have in excess of six iterations, we
obtain the result with high accuracy by taking scaling factor:
𝐾 ≈ cos 26.55° cos 45° … … . cos 0.8995° = 0.5967

11. Conclusion
› In conclusion, we can say that if we do not use cosine in the
equation and use scaling factor of 0.5967 instead, we would
obtain an ideal rotation.
› For all the additionally referencing application, here we can
consider the figures of scaling factor.
› This inside and out comes to no detriment considering the
way that, as clarified in the model close to the completion of
the paper, the scaling factor is ordinarily dealt with as a key
motivator in the system.

12. Thank you..