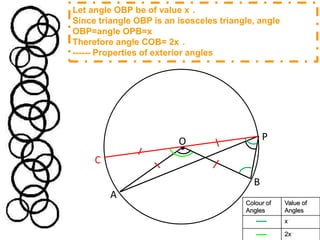
Method One proves that the angle at the centre (Angle AOB) is twice the angle at circumference (Angle APB) by showing that triangles OBP and OAP are isosceles triangles, which allows calculating the angles. Method Two extends a radius to form a diameter and shows that triangles OCA, OAP and OBP are isosceles triangles. It then uses properties of exterior angles to calculate that the angle at the centre (Angle AOB) is twice the angle at circumference (Angle APB). Both methods demonstrate the relationship between the angles at the centre and circumference of a circle.

1. Method One

2. Let Angle AOB be x°.We draw a line from O to P. Since lines OP, OB and OA are radii of the same circle, they are equal in length. From that, we can conclude that triangles OBP and OAP are isosceles triangles.POBA

3. Let Angle BOP be y°.Angle OBP = Angle OPB = (180°-y°)/2------------- Sum of interior angles of a triangle is 180°------------- Property of isosceles triangle POBA

4. Angle AOP = x°+y°Angle OAP = Angle OPA = (180°-x°-y°)/2------------- Sum of interior angles of a triangle is 180°------------- Property of isosceles triangle POBA

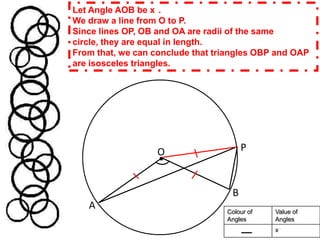
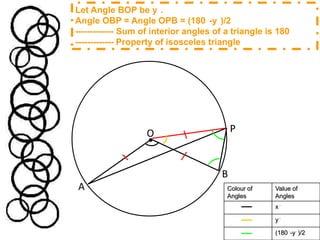
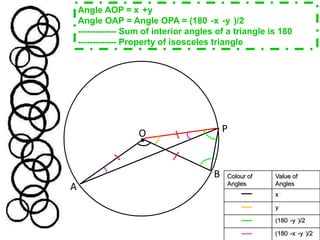
5. Angle APB = Angle OPB – Angle OPA = [(180°-y°)/2] – [(180°-x°-y°)/2] = (180°-y°-180°+x°+y°)/2 = x°/2POBATherefore, this proves that the angle at the centre (Angle AOB = x°) is twice the angle at circumference (Angle APB = x°/2)

6. Method TWO

7. We draw a line form P to O and extend it out to C, forming the diameter of the circle.Therefore OC=OC=OB=OP since they are all radii of the circle.Thus triangles OCA, OAP and OBP is isosceles.POCBA

8. Let angle OBP be of value x°.Since triangle OBP is an isosceles triangle, angle OBP=angle OPB=x°Therefore angle COB= 2x°.------ Properties of exterior anglesPOCBA

9. Let angle OAP be of value y°.Since triangle OAP is an isosceles triangle, angle OAP=angle OPA=y°Therefore angle COA= 2y°.------ Properties of exterior anglesPOCCBA

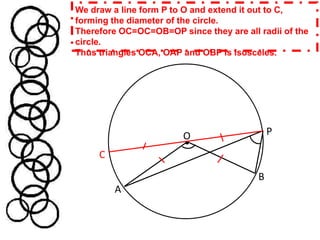
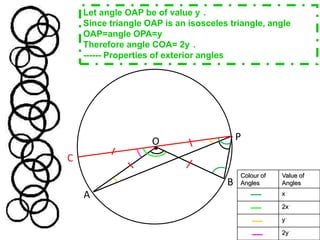
10. Angle AOB= angle COB-angle COA = 2x°-2y° = 2(x-y)°Angle APB= angle OPB-angle OPA = x°- y° = (x-y)°POCBATherefore, this proves that the angle at the centre [Angle AOB = 2(x-y)°] is twice the angle at circumference [Angle APB = (x-y)°].