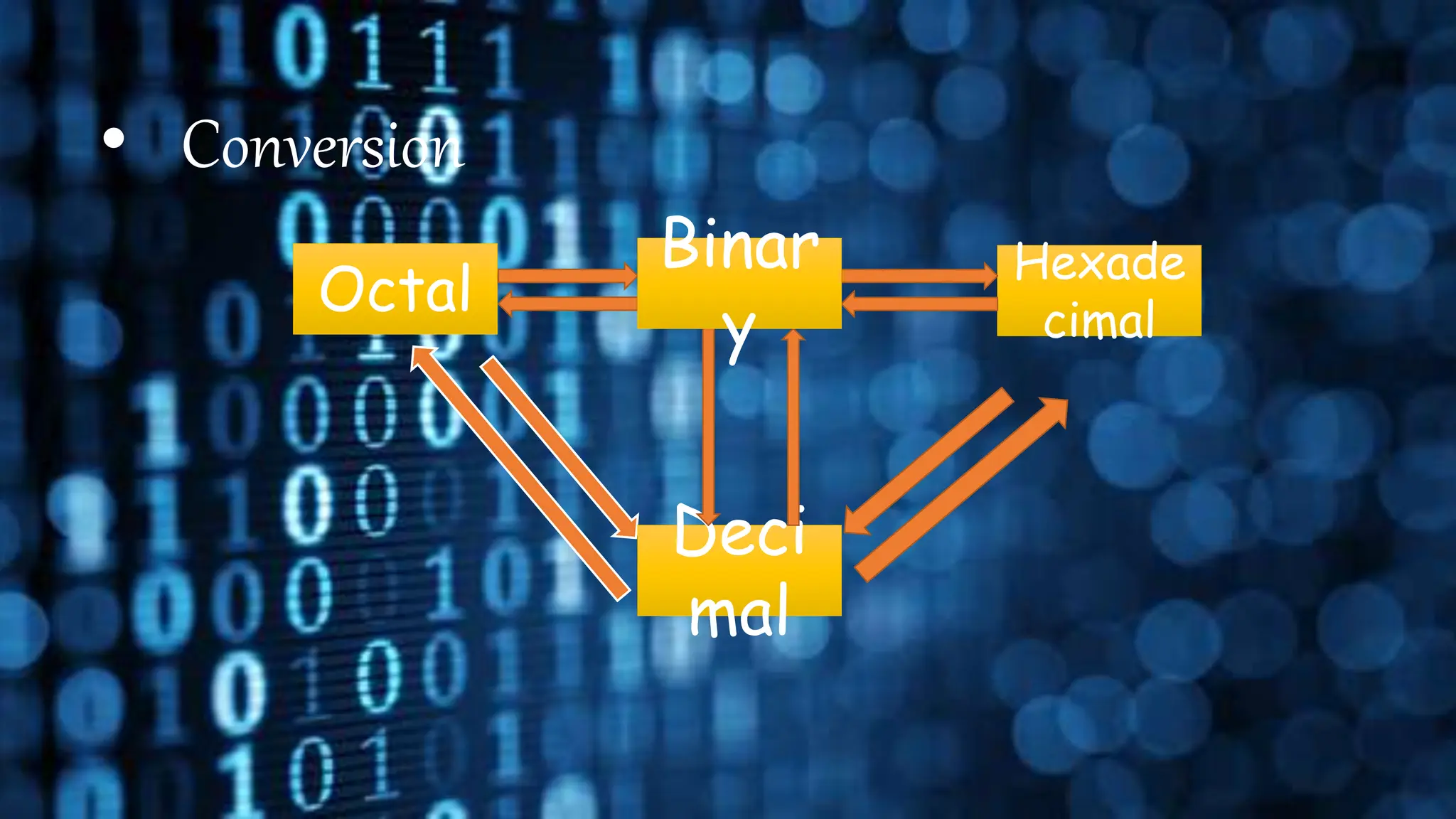
This document discusses different number systems including positional and non-positional systems. It provides examples of the binary, octal, decimal, and hexadecimal number systems. It also describes how to convert between these different number systems by first converting to decimal as an intermediate step if needed.

1. Number System

2. Number
System
Non-Positional Number
System
Positional Number System

3. Number System
• Number system can be defined as a set of symbols(digits) that
represent a value. Different number systems may use same
digit but represent value or even in same number system a
notation can have two values.
• Example: Decimal system and binary system both contain the
digit “1” but have different values when used. In decimal “11”
is eleven but in binary “11” is read as “one one” and it’s
decimal equivalent is 3.
• Similarly in roman numeral “I” is 1 and “V” is 5 but when
writing 4 “IV” is written making the value of “V” 5.

4. Positional Number System
• The number system in which a digit when in a specific place of
a number has a fixed value no matter the digit is called
Positional Number system. Simply, the system in which the
position of a digit determines it’s value is called positional
number system.
•

5. Non-Positional Number System
• The number system in which a digit has same value no matter of it’s
position and doesn’t follow a specific pattern of logic in counting is
called non-positional number system.
• In roman number system I represents 1, V represents 5, X represents 10,
L represents 50, C represents 100, D represents 500, M represents 1000.
This is true no matter how the digits are arranged although the
arrangement of digits make a difference in resultant value.
• Example: IV is 4 and VI is 6. The logic here is that the digit written ahead
is subtracted and the digit written behind is added but in both cases I is
one and V is 5.

6. Binary Number System
• Binary number system is the
numeric number system followed by
all the computers. It consists of 2
digits ‘0’ and ‘1’ thus is called
binary number system.
Decimal Binary
0 0
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111

7. Octal Number System
• Octal number system is the
numeric number system made
of 8 digits from ‘0’ to ‘8’.
Decimal Octal
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 10
9 11
10 12
11 13
12 14
13 15
14 16
15 17

8. Decimal Number System
• Decimal number system is the numeric
number system normally used number
system in all of the mathematical and
scientific calculations.
Decimal
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

9. Hexadecimal Number System
• Hexadecimal number system is the
alphanumeric number system that
consists of digit from ‘0-9’ and English
alphabets ‘A-F’.
Decimal Hexadecima
l
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10 A
11 B
12 C
13 D
14 E
15 F

10. • Things to remember
A number is always written within
brackets and it’s radix must be
written. Radix is the number of
digits in the system.
Binary: (101101)2 -2 is the radix
Octal: (654)8 -8 is the radix
Decimal: (198)10 -10 is the radix
Hexadecimal: (6A5)16 -16 is the radix
Binary Subtraction:
0-0=0
1-0=1
0-1 [Not Possible]
1-1=0
10-1=1

11. • Conversion
Octal
Deci
mal
Hexade
cimal
Binar
y

12. Simplify
Add power from left starting with zero.
Break the number into individual digit.
Let a binary number (10011)2.
BINARY TO DECIMAL

13. Simplify
Add power from left starting with zero.
Break the number into individual digit.
Let a octal number
(12537)8.
OCTAL TO DECIMAL

14. Simplify
Add power from left starting with zero.
Break the number into individual digit.
Let a hexadecimal number
(3AD4)2.
HEXADECIMAL TO DECIMAL

15. DECIMAL TO BINARY
Let a decimal number (34)2.
Take the number and divide it by 2 while
noting the remainder.
- - REM
2 34 0
2 17 1
2 8 0
2 4 0
2 2 0
2 1 1
0
Write the number starting from bottom.

16. DECIMAL TO OCTAL
Let a decimal number (225)2.
Take the number and divide it by 8 while
noting the remainder.
- - REM
8 225 1
8 28 4
8 3 3
0
Write the number starting from bottom.

17. DECIMAL TO HEXADECIMAL
Let a hexadecimal number (612)2.
Take the number and divide it by 16 while
noting the remainder.
- - REM
16 612 4
16 38 6
16 2 2
0
Write the number starting from bottom.

18. BINARY TO OCTAL
Let a binary number
(100111101)2.
Break the number into 3 digit groups from
left
100111101
Write equivalent octal digit for each
binary group.
Group each digit and write them together.

19. Let a binary number
(101011111010)2.
Break the number into 4 digit groups from
left
101011111010
Group each digit and write them together.
BINARY TO HEXADECIMAL

20. OCTAL TO BINARY
To convert octal to binary, follow the given steps:
1. Convert the octal to decimal,
2. Then convert the decimal to binary

21. HEXADECIMAL TO BINARY
To convert hexadecimal to binary, follow the given
steps:
1. Convert the hexadecimal to decimal,
2. Then convert the decimal to binary