Download as PDF, PPTX
Uploaded byCarlo Taticchi
A Tool For Ranking Arguments Through Voting-Games Power Indexes
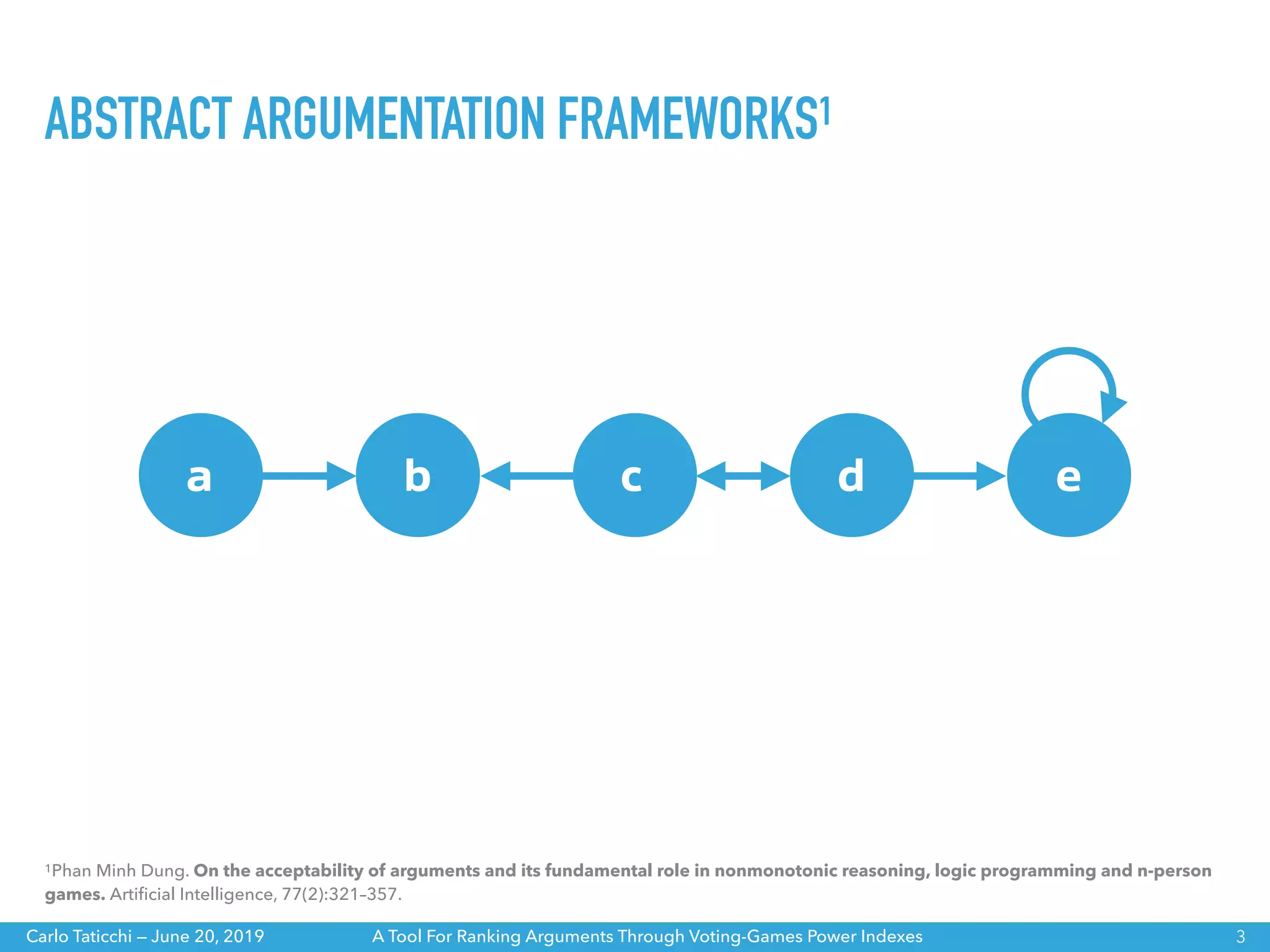
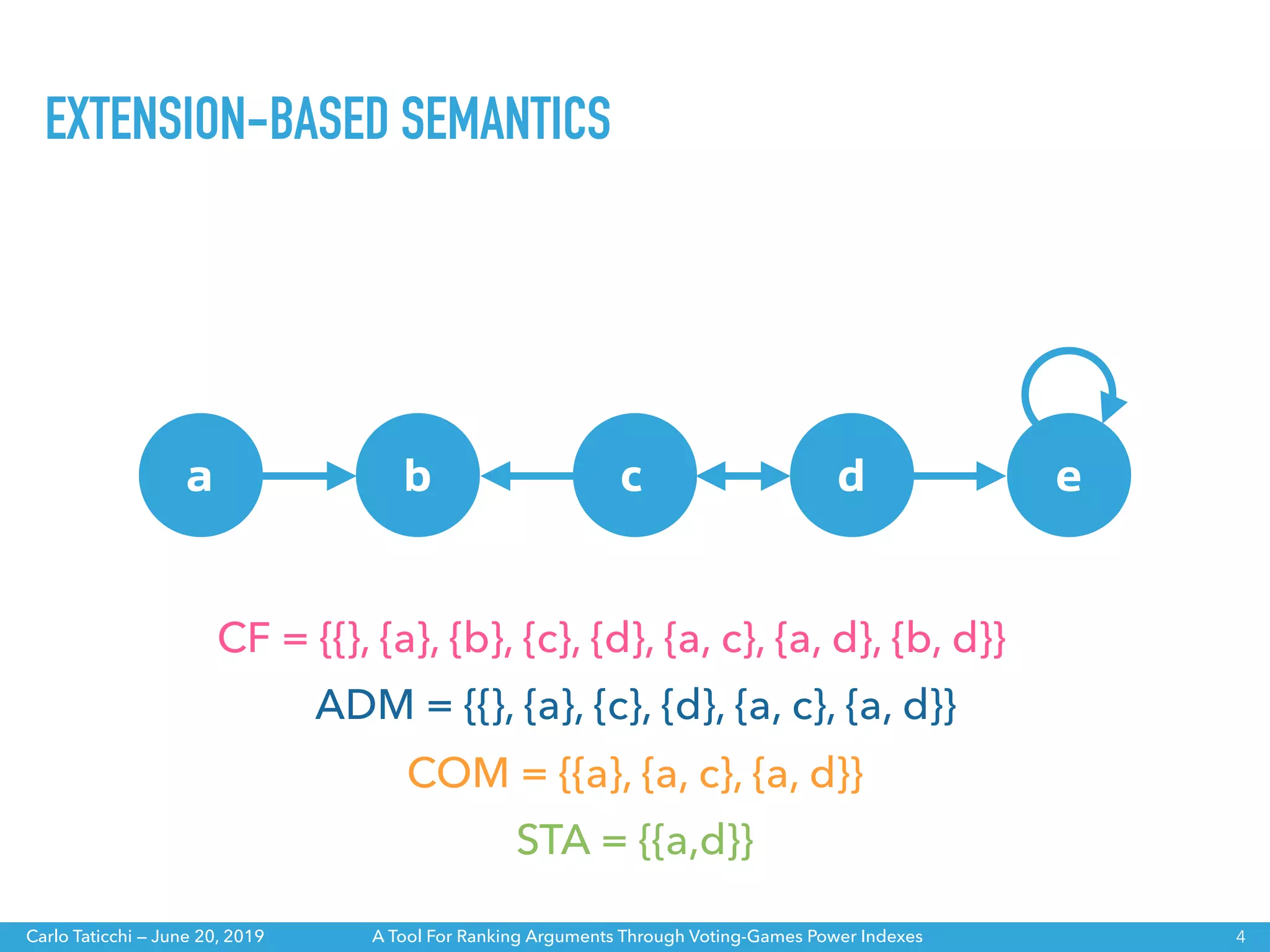
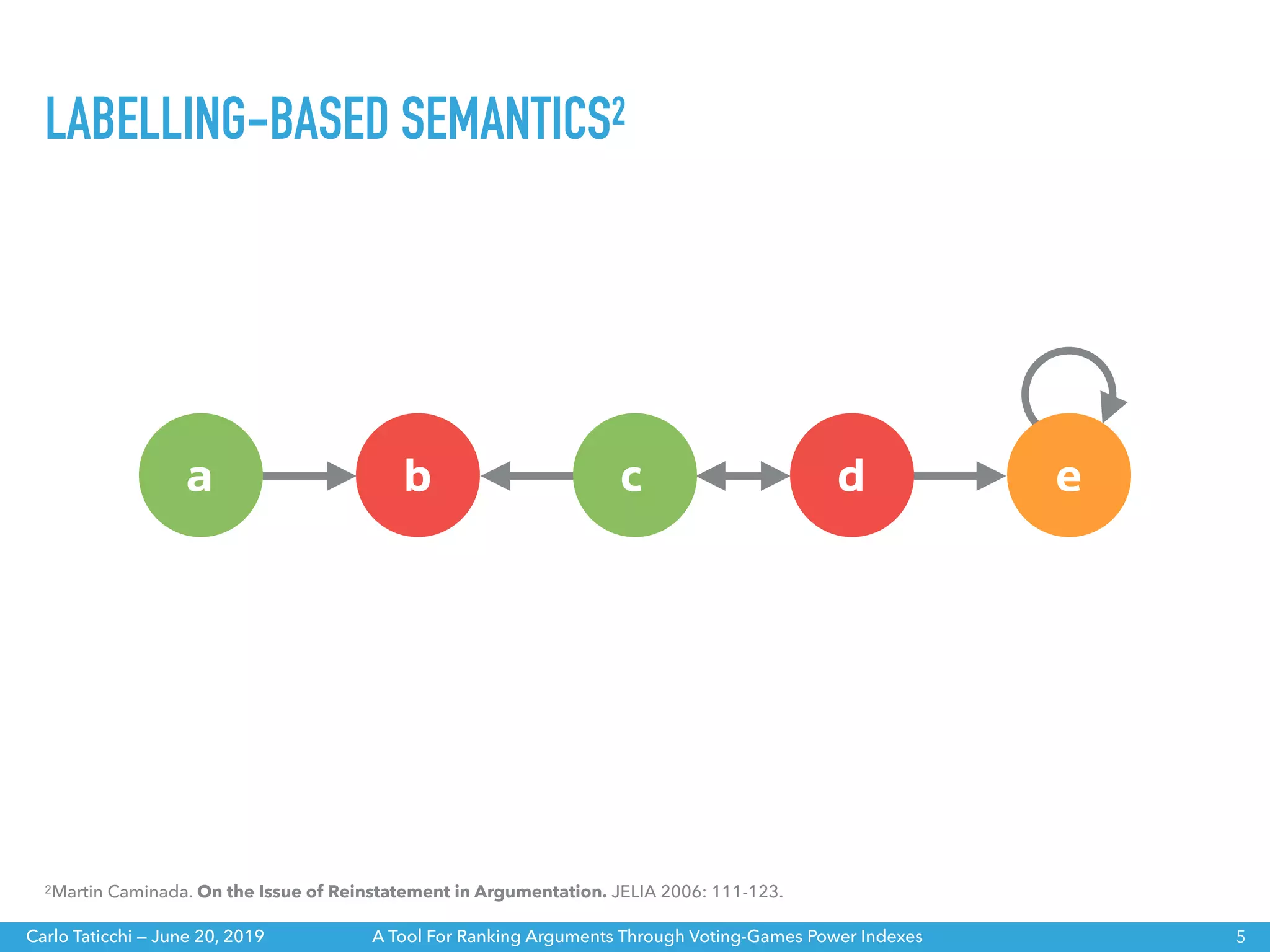
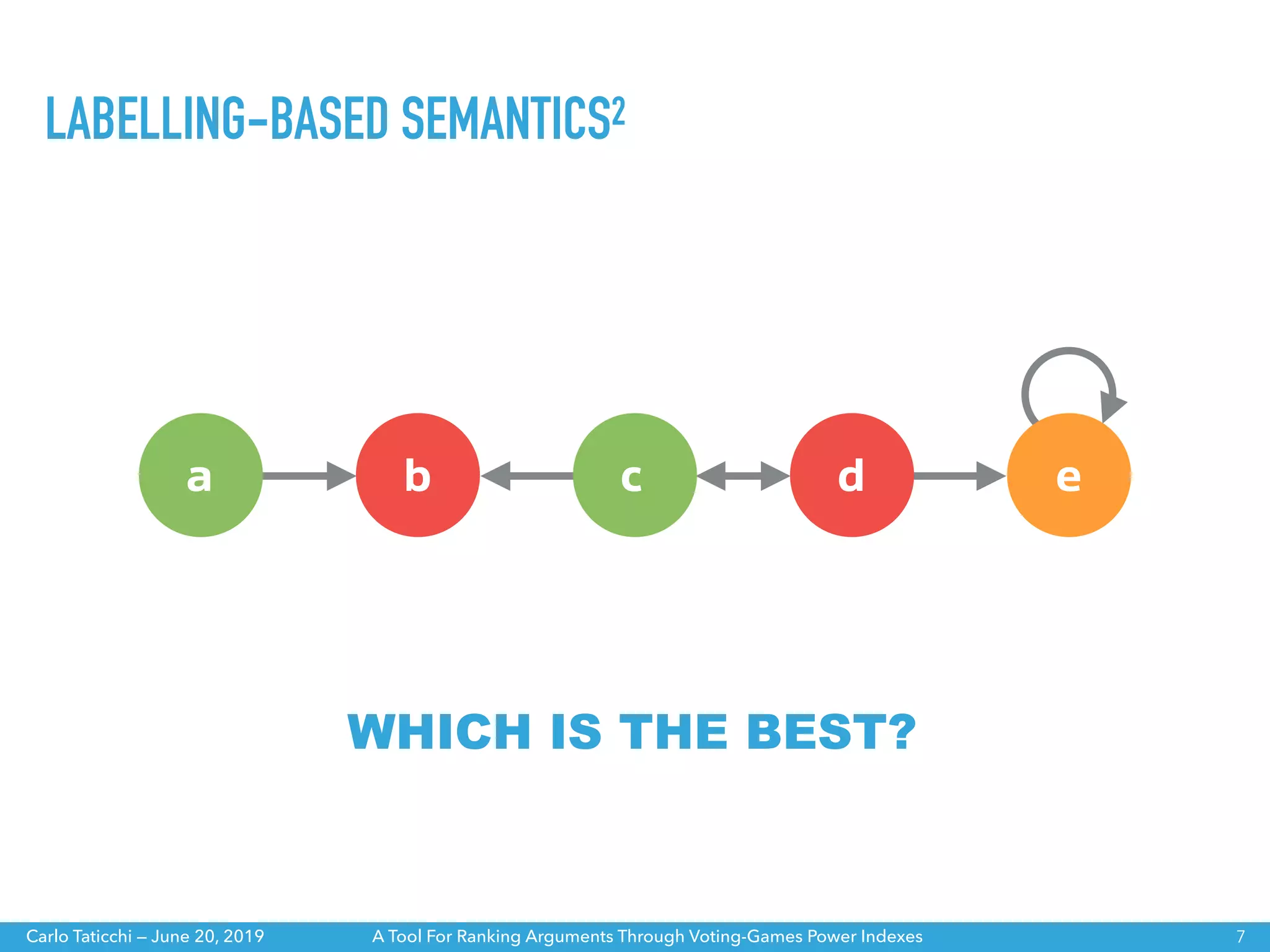
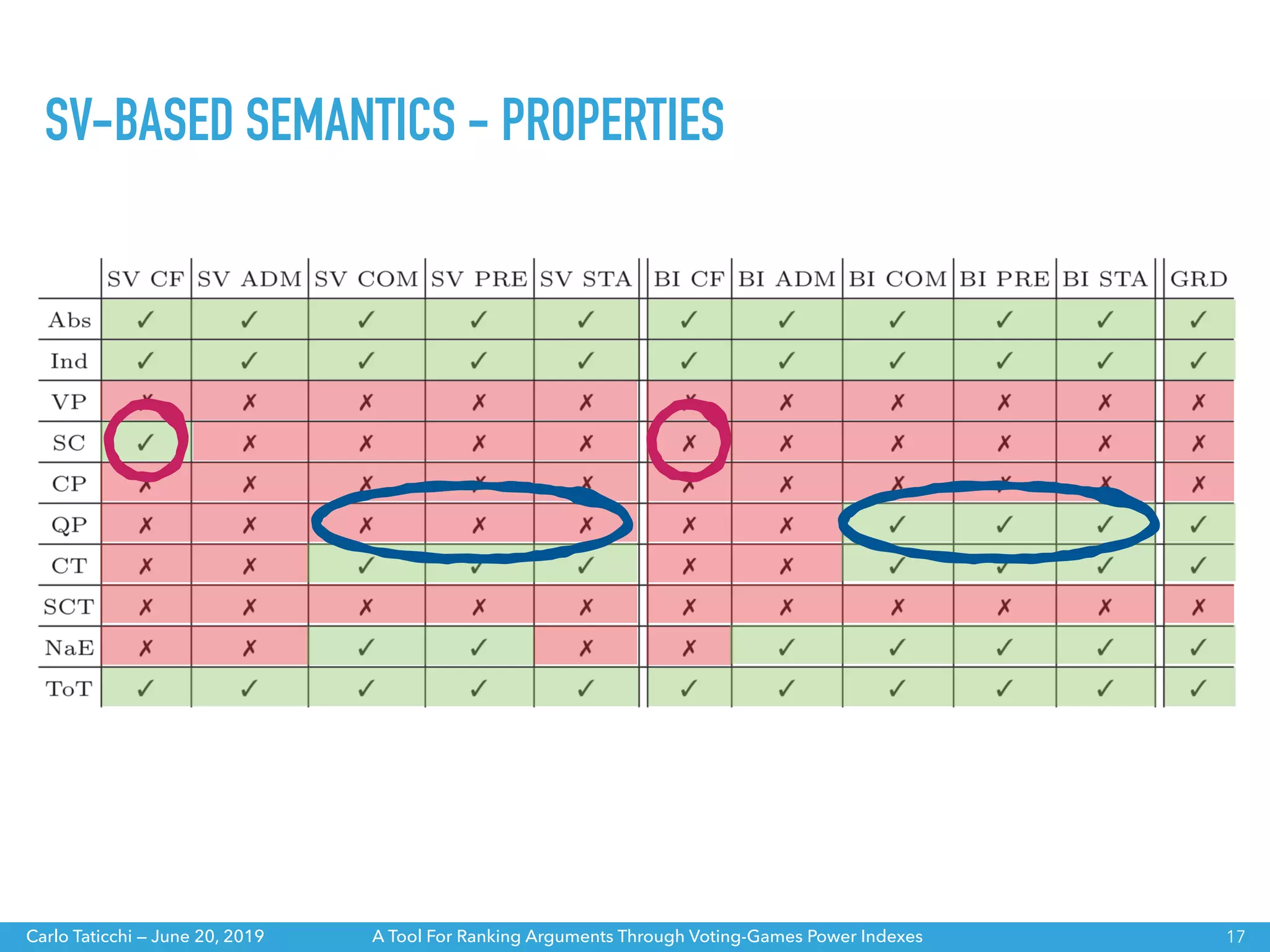
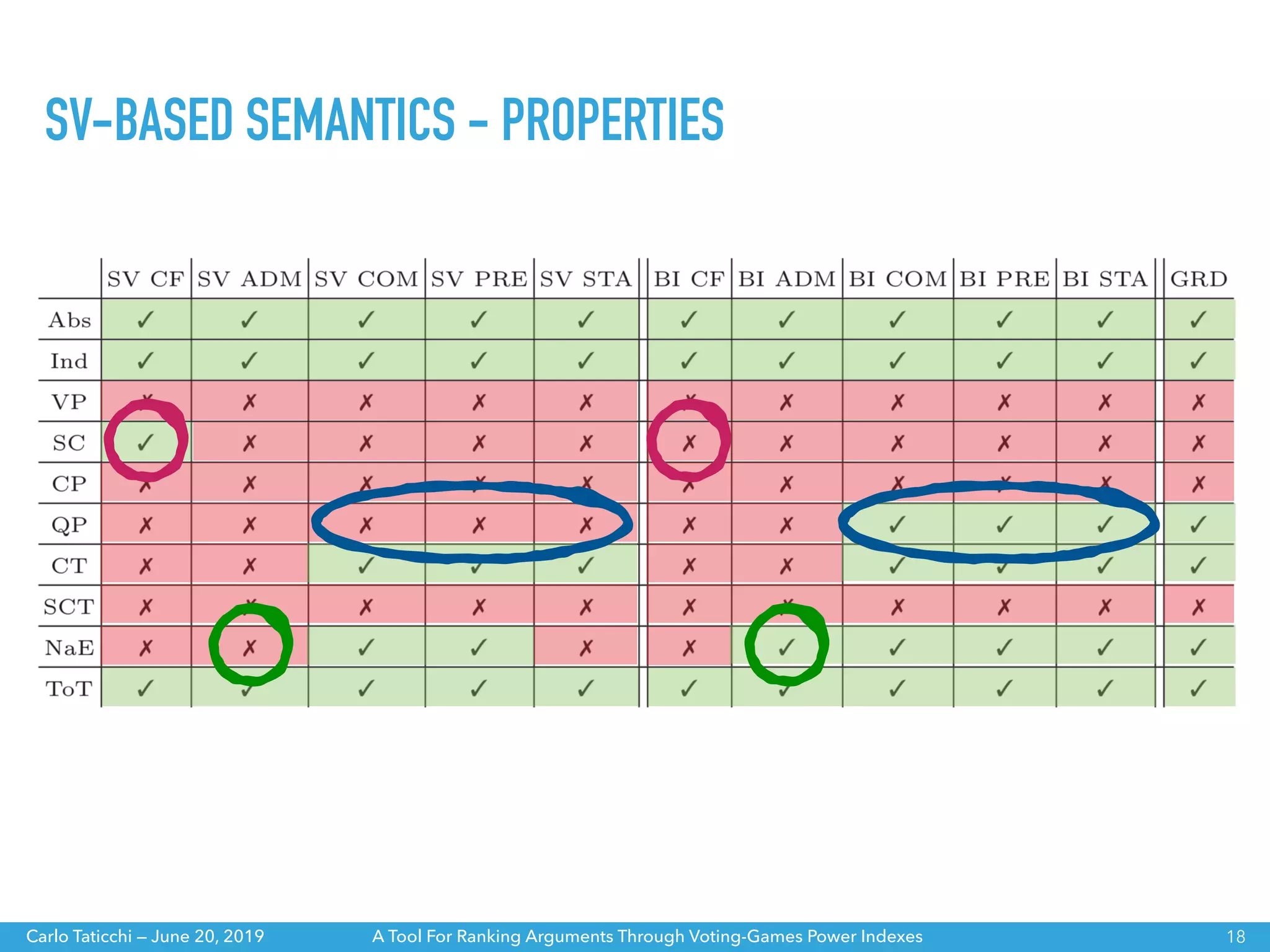
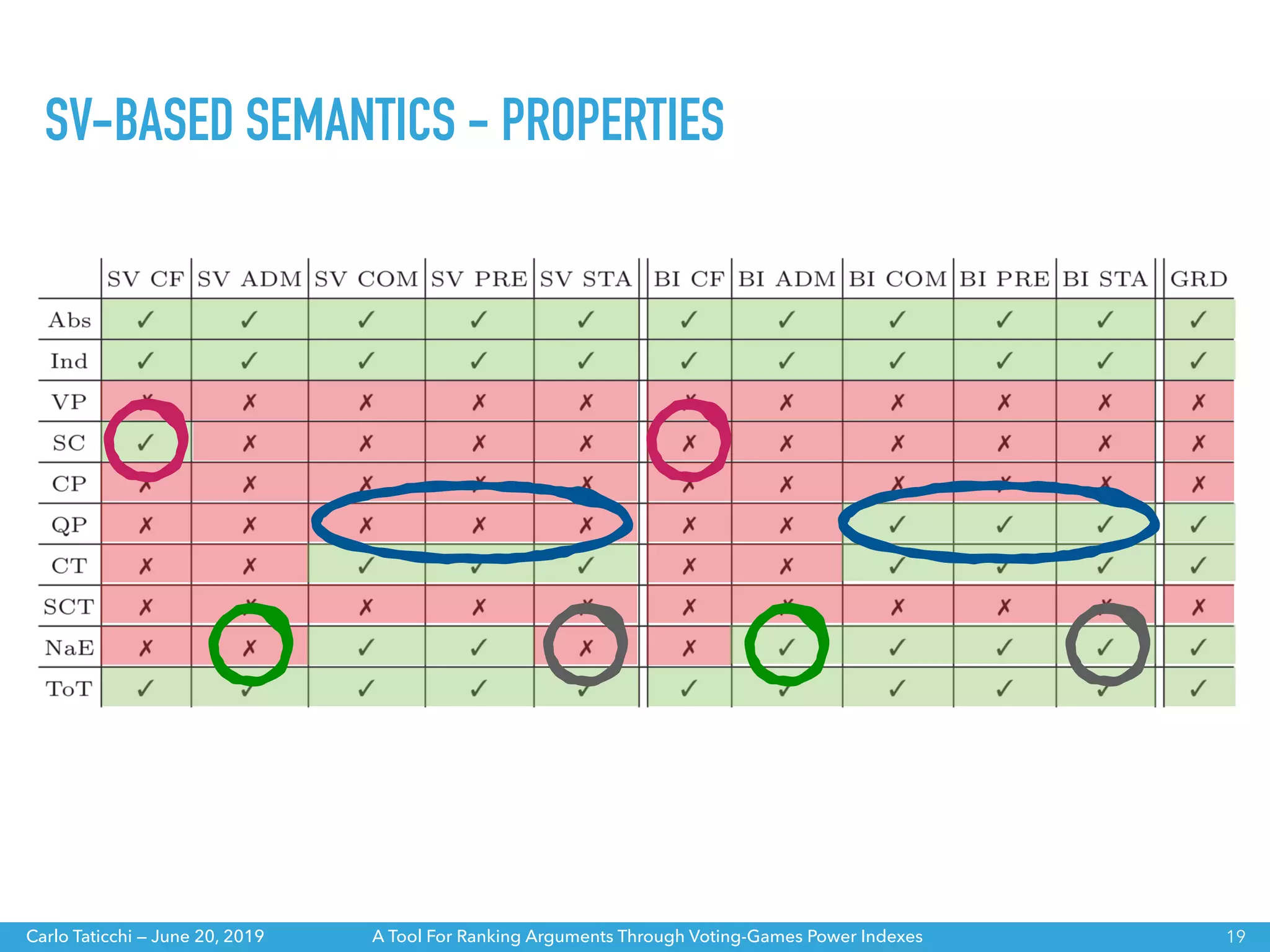
The document discusses a tool for ranking arguments using voting-game power indexes, exploring concepts from argumentation theory and various semantics. It covers different approaches such as ranking-based and labelling-based semantics, as well as specific power indexes like Shapley value and Banzhaf index. The tool aims to help understand the differences between these indexes and their impacts on argumentation frameworks.
A Tool For Ranking Arguments Through Voting-Games Power Indexes
- 1. A TOOL FORRANKING ARGUMENTS THROUGH VOTING-GAMES POWER INDEXES Stefano Bistarelli, Francesco Faloci, Francesco Santini and Carlo Taticchi
- 2. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 INDEX ▸ Argumentation Theory ▸ Argumentation Semantics ▸ Power Indexes ▸ Definitions ▸ SV-based semantics ▸ Description + Example ▸ Conclusion 2 ConArg
- 3. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 ABSTRACT ARGUMENTATION FRAMEWORKS1 3 a b c d e 1Phan Minh Dung. On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artificial Intelligence, 77(2):321–357.
- 4. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 EXTENSION-BASED SEMANTICS 4 a b c d e ADM = {{}, {a}, {c}, {d}, {a, c}, {a, d}} CF = {{}, {a}, {b}, {c}, {d}, {a, c}, {a, d}, {b, d}} STA = {{a,d}} COM = {{a}, {a, c}, {a, d}}
- 5. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 LABELLING-BASED SEMANTICS2 5 a b c d e 2Martin Caminada. On the Issue of Reinstatement in Argumentation. JELIA 2006: 111-123.
- 6. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 LABELLING-BASED SEMANTICS2 6 a b c d e IN if it is attacked only by OUT arguments OUT if it is attacked by at least an IN argument UNDEC otherwise 2Martin Caminada. On the Issue of Reinstatement in Argumentation. JELIA 2006: 111-123.
- 7. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 7 a b c d e WHICH IS THE BEST? LABELLING-BASED SEMANTICS2
- 8. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 RANKING-BASED SEMANTICS3 ▸ Transforms an Argumentation Framework into a ranking ▸ Criteria: direct attacks, lengths of the incoming paths, rewards ▸ Good properties 8 3Leila Amgoud, Jonathan Ben-Naim. Ranking-Based Semantics for Argumentation Frameworks. SUM 2013: 134-147. ≻a d ≻c ≻e ≻ b
- 9. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 ▸ Abstraction ▸ Independence ▸ Void Precedence ▸ Self-contradiction ▸ Cardinality Precedence RANKING-BASED SEMANTICS - PROPERTIES4 ▸ Quality Precedence ▸ Counter-Transitivity ▸ Strict Counter-Transitivity ▸ Defense Precedence ▸ Non-attacked Equivalence 9 4Elise Bonzon, Jérôme Delobelle, Sébastien Konieczny, Nicolas Maudet. A Comparative Study of Ranking-Based Semantics for Abstract Argumentation. AAAI 2016: 914-920.
- 10. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 POWER INDEXES ▸ Shapley Value ▸ Banzhaf Index ▸ Deegan-Packel ▸ Johnstone 10
- 11. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 ▸ Banzhaf Index ϕi(v) = ∑ S−i ⊆ G ∖ {i} s!(n − 1 − s)! n! (v(S−i ∪ {i}) − v(S−i)) βi(v) = 1 2|N|−1 ∑ S ⊆ N ∖ {i} (v(S ∪ {i}) − v(S)) ▸ Shapley Value POWER INDEXES 11
- 12. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 vI σ,F(S) = { 1, if S ∈ in(Lσ) 0, if otherwise RANKING FUNCTIONS 12 a b c d e
- 13. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 vI σ,F(S) = { 1, if S ∈ in(Lσ) 0, if otherwise vO σ,F(S) = { 1, if S ∈ out(Lσ) 0, if otherwise RANKING FUNCTIONS 13 a b c d e In the event of a tie
- 14.
- 15. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 SV-BASED SEMANTICS - PROPERTIES 15
- 16. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 SV-BASED SEMANTICS - PROPERTIES 16
- 17. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 SV-BASED SEMANTICS - PROPERTIES 17
- 18. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 SV-BASED SEMANTICS - PROPERTIES 18
- 19. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 SV-BASED SEMANTICS - PROPERTIES 19
- 20. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 CONCLUSION 20 ▸ Tool available at www.dmi.unipg.it/conarg ▸ Ranking-based semantics • Shapley Value • Banzhaf Index • Deegan-Packel • Johnstone
- 21. A Tool ForRanking Arguments Through Voting-Games Power IndexesCarlo Taticchi — June 20, 2019 NEXTCONCLUSION 21 ▸ Understand the differences between Power Indexes ▸ Capture global properties: • structure of the AF • full attacking paths ▸ Tool available at www.dmi.unipg.it/conarg ▸ Ranking-based semantics • Shapley Value • Banzhaf Index • Deegan-Packel • Johnstone
- 22. A TOOL FORRANKING ARGUMENTS THROUGH VOTING-GAMES POWER INDEXES Thanks for your attention!