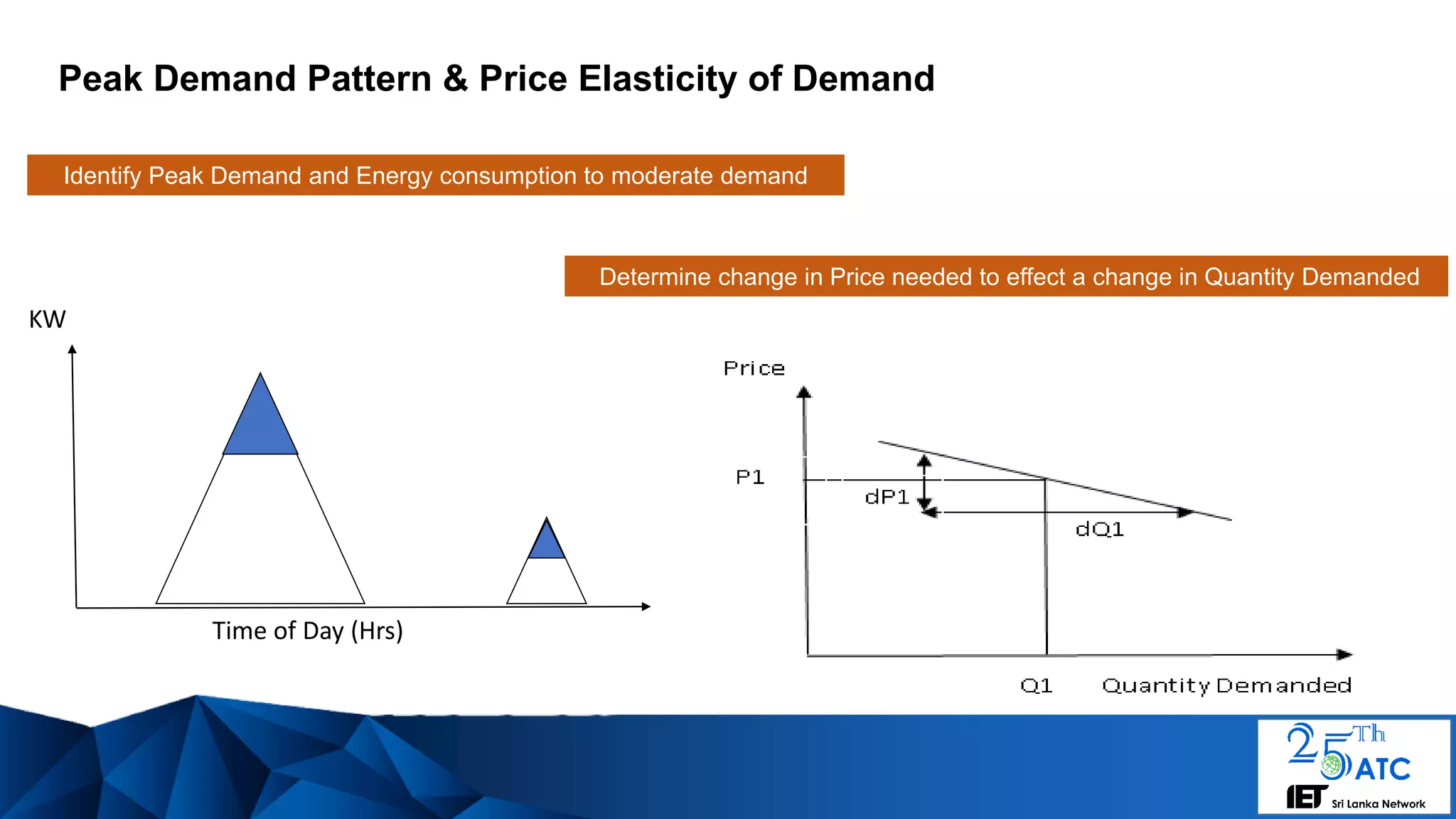
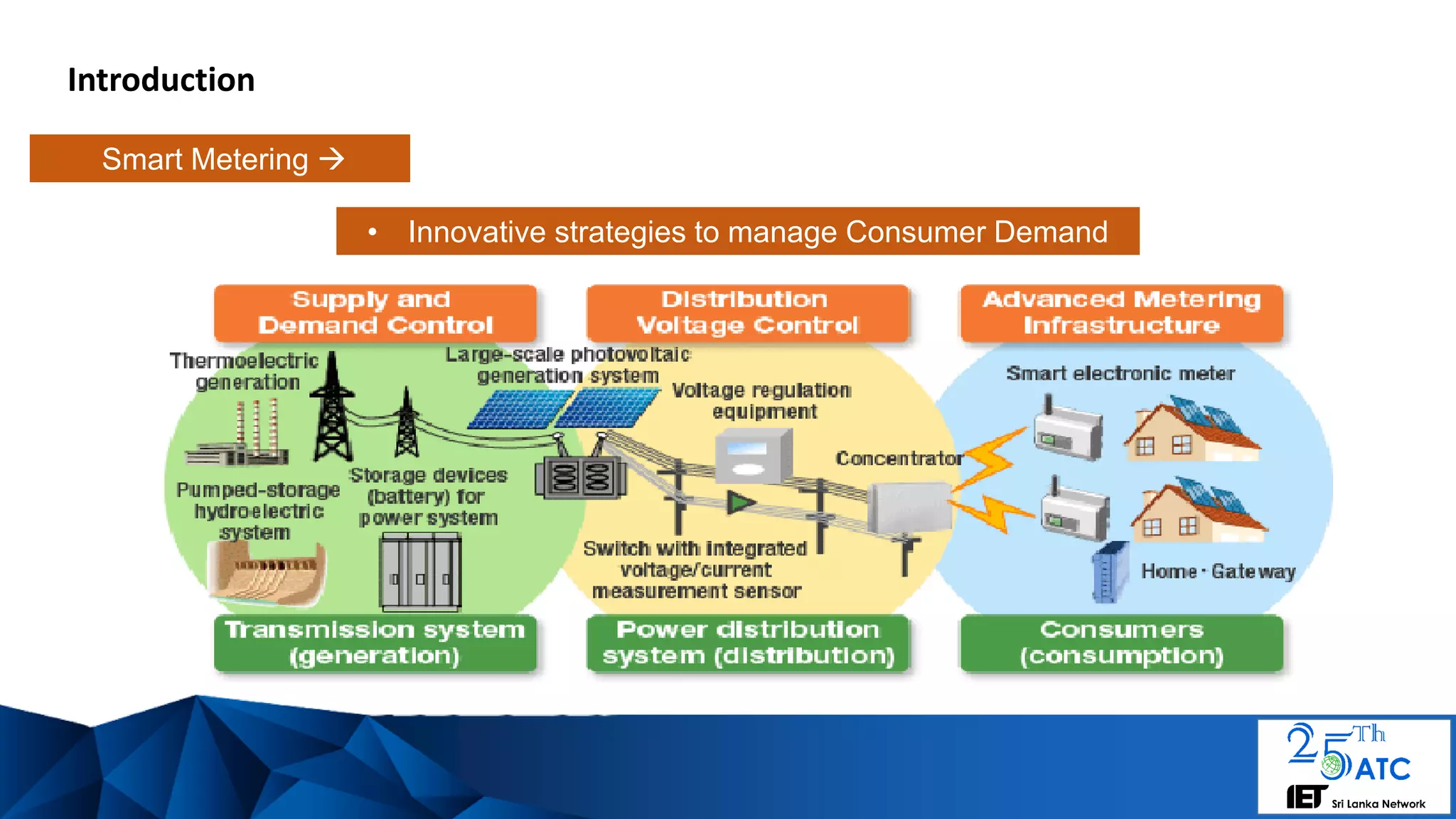
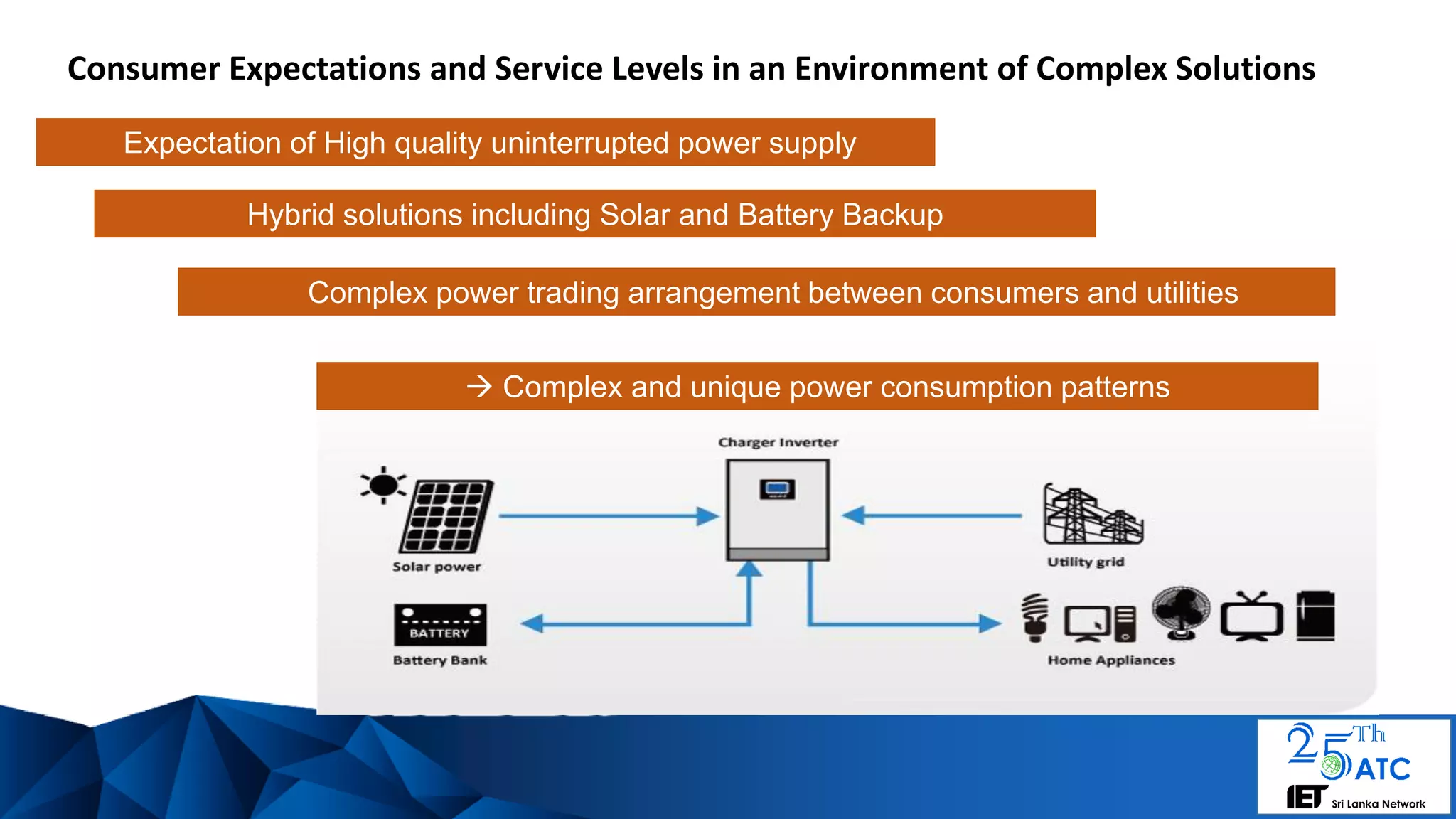
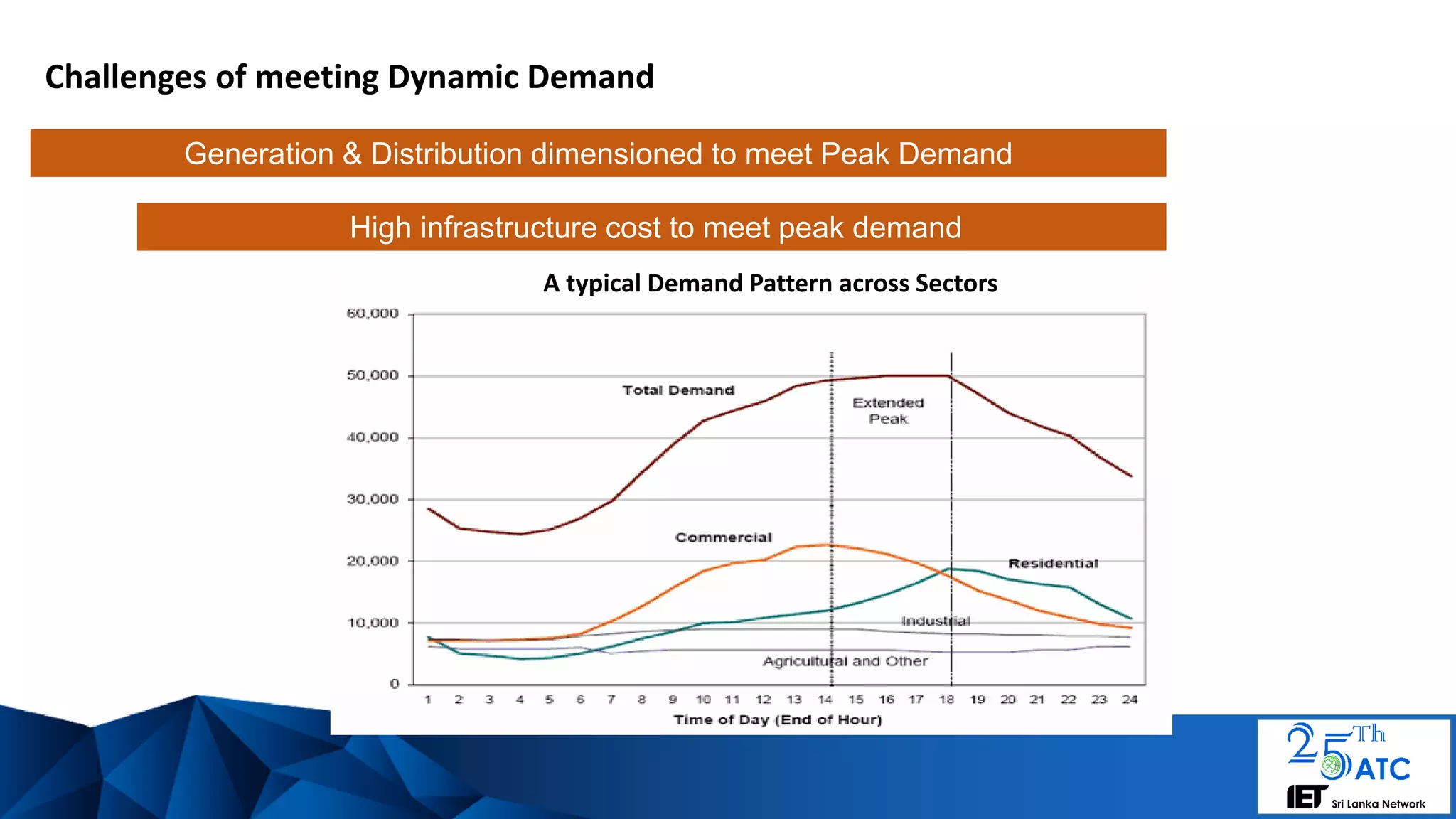
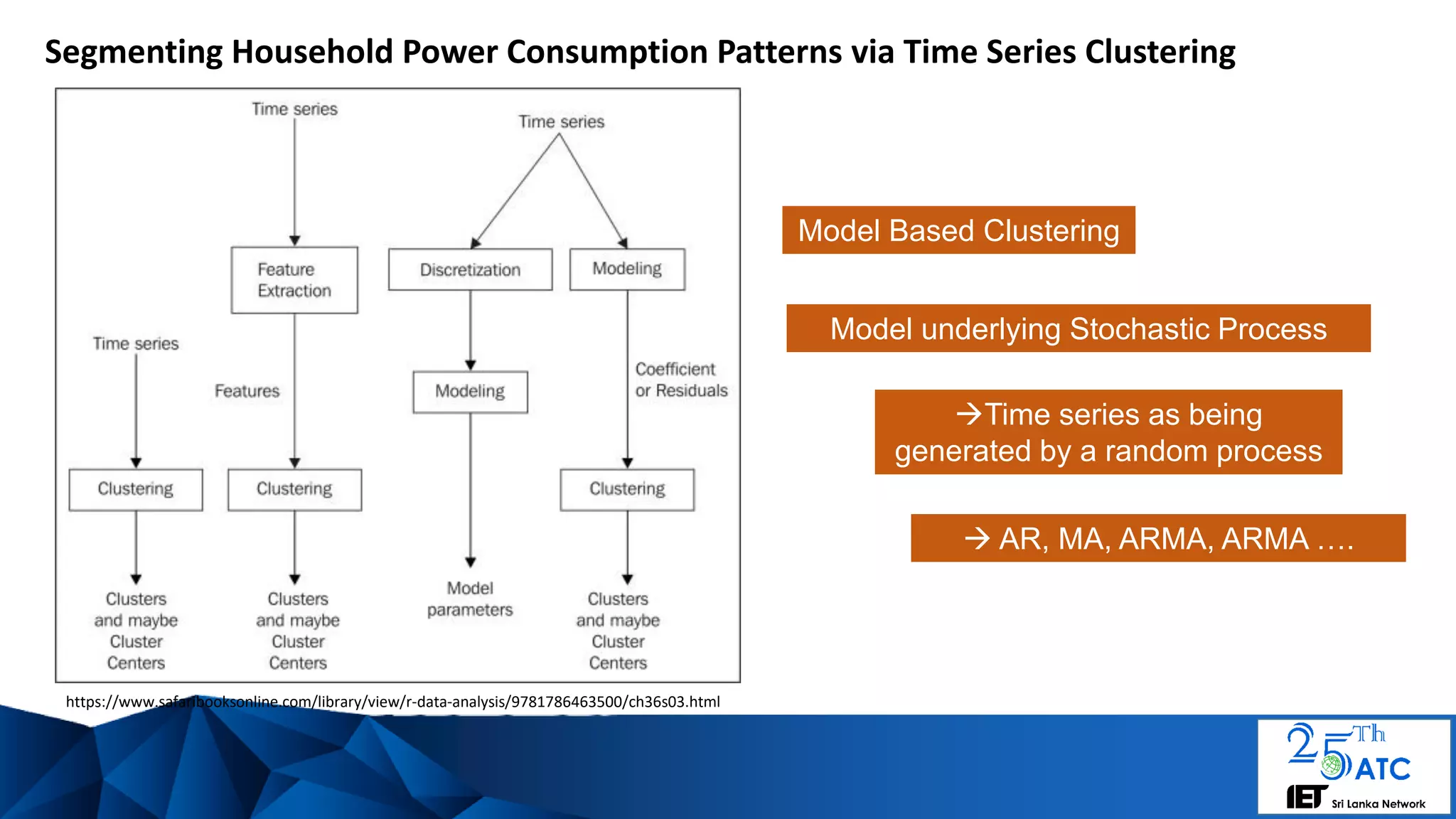
The document discusses a framework for dynamic electricity pricing based on time series clustering of consumer demand patterns to manage consumer expectations and utility supply. It emphasizes the complexities of consumer demand, strategies for segmenting power consumption, and modeling using autoregressive integrated moving average (ARIMA) methods. Additionally, it suggests that unique dynamic pricing strategies can be implemented to address peak demand and identify outlier consumption patterns.

1. 25th Annual Technical Conference - 2018
Author:
Asoka Korale, Ph.D., C.Eng., MIET
A Framework for Dynamic Pricing Electricity
Consumption Patterns via Time Series
Clustering of Consumer Demand

2. Introduction
• Innovative strategies to manage Consumer Demand
Smart Metering 

3. Consumer Expectations and Service Levels in an Environment of Complex Solutions
Expectation of High quality uninterrupted power supply
Complex power trading arrangement between consumers and utilities
Hybrid solutions including Solar and Battery Backup
 Complex and unique power consumption patterns

4. Challenges of meeting Dynamic Demand
Generation & Distribution dimensioned to meet Peak Demand
A typical Demand Pattern across Sectors
High infrastructure cost to meet peak demand

5. Imperatives for Managing Consumer Demand
Peak demand in a segment considerably higher than average
Different segments have different patterns
Managing Consumer Demand a key Strategy of the Utility
Lower operating costs Lower infrastructure costs
Lower / manage the risks of outages
Ensure better quality of supply
More predictable

6. Segmenting Household Power Consumption Patterns via Time Series Clustering
Model underlying Stochastic Process
 AR, MA, ARMA, ARMA ….
Model Based Clustering
https://www.safaribooksonline.com/library/view/r-data-analysis/9781786463500/ch36s03.html
Time series as being
generated by a random process

7. Hannan-Rissanen Algorithm to Estimate Parameters of ARMA(p,q)
qnqnnpnpnn bbYaYaY    ...... 1111
Initial parameter estimate as high order (m)
pure AR process

































)(
...
)1(
..
)0(...)1(
.........
)1(...r(0) 1
mr
r
rmr
mr
m

npnmnn YYY    ...11
Yule-Walker Equations to estimate AR parameters
mnmnnn YYY    ...11
Error term via pure high order AR process

8. Hannan-Rissanen Algorithm to Estimate parameters of ARMA(p,q)
Least squares to estimate ARMA parameters
mM 
mMMM TT 1
)( 

Populate matrix with lagged error terms estimated via pure AR process
nnn YY ˆ
which with some
modifications can
be put in the form
forming a least squares estimate for the ARMA parameters
qnqnpnpnn bbYaYaY    ......ˆ
1111where




































































qpn
pn
pn
n
q
p
qpnqpnqpn
qnnpnn
y
y
y
y
b
b
a
a
y
yy
...
...
...
...
1
...
......
1
1
1
21
1


]...[ 11 qp bbaa

9. Frequency Response from Pole Zero Map
)(
]...a[1
]...b[1
Y(z) 1
1
1
1
zE
zaz
zbz
p
p
q
q





B(z)
A(z)
n nY
Digital Signal Processing by Proakis and Manolakis
H = Y(z)/E(z) as product of complex roots

10. log(MSE(p+q))
AIC(p+q)
Model Order (p+q)
Akaike Information Criteria
Tradeoff between model complexity and prediction error
AIC = log(error variance or sum of squared prediction error) + 2*(p+q)
Minimum point of AIC curve gives optimum trade off
between model complexity and variance in error

11. Conditions of the Sample Survey
104 power consumption patterns
Each pattern an average over one month of weekdays
96 power measurements at 15 minute intervals in a day
Households in the Rajagiriya Area
Diverse sample of Households

12. Total System Power Consumption Pattern
Two peak periods
Peak a 66% increase over mean
of considerable length: 2.5 Hrs & 3 Hrs
Aggregate behavior less volatile
104 households at 15 minute intervals

13. ARMA Modeling of Power Consumption Patterns
Time series of complexity ARMA(1,2) Clustering ARMA(1,2) Parameters
Large majority in cluster Close correspondence between model parameters

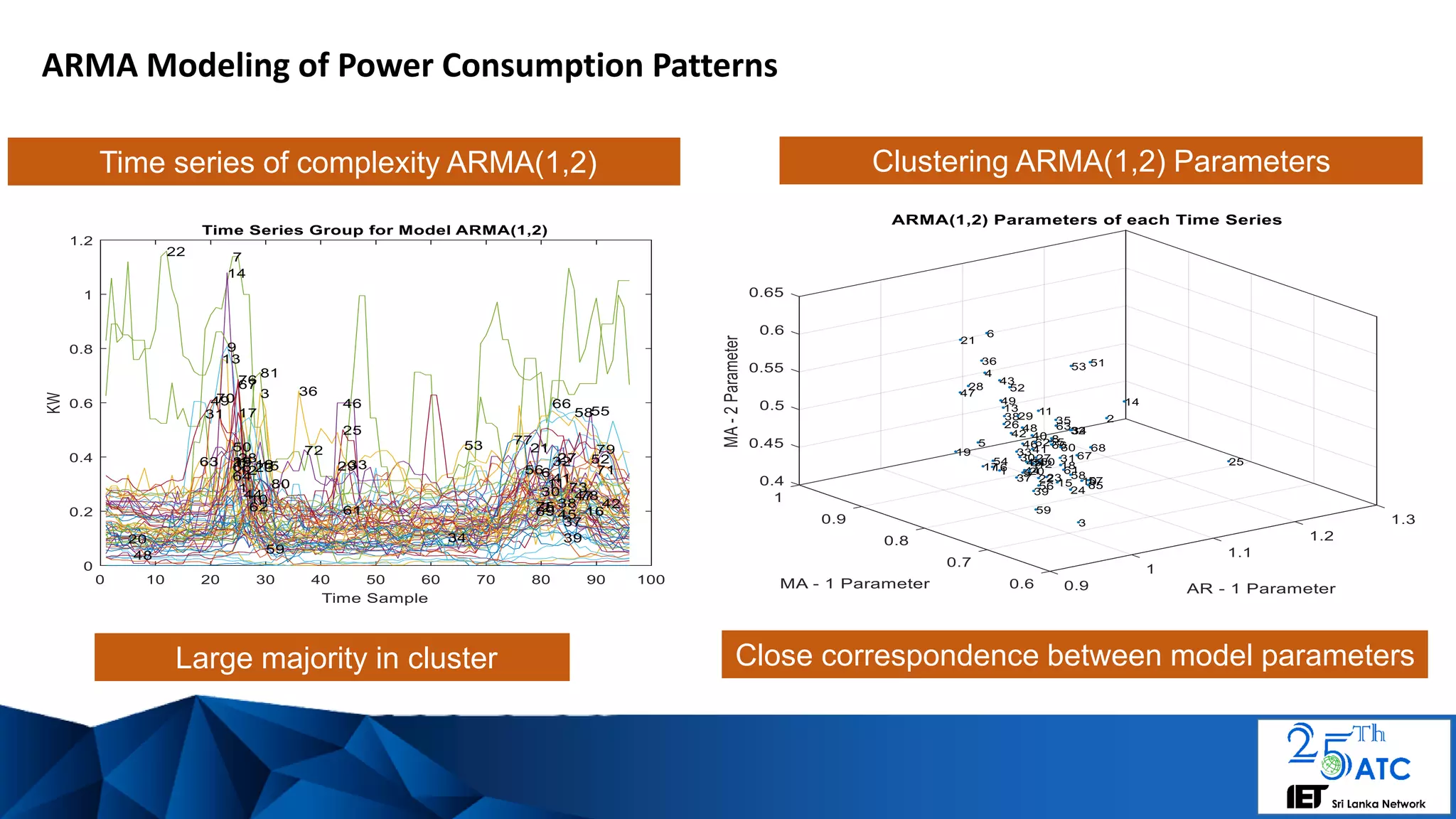
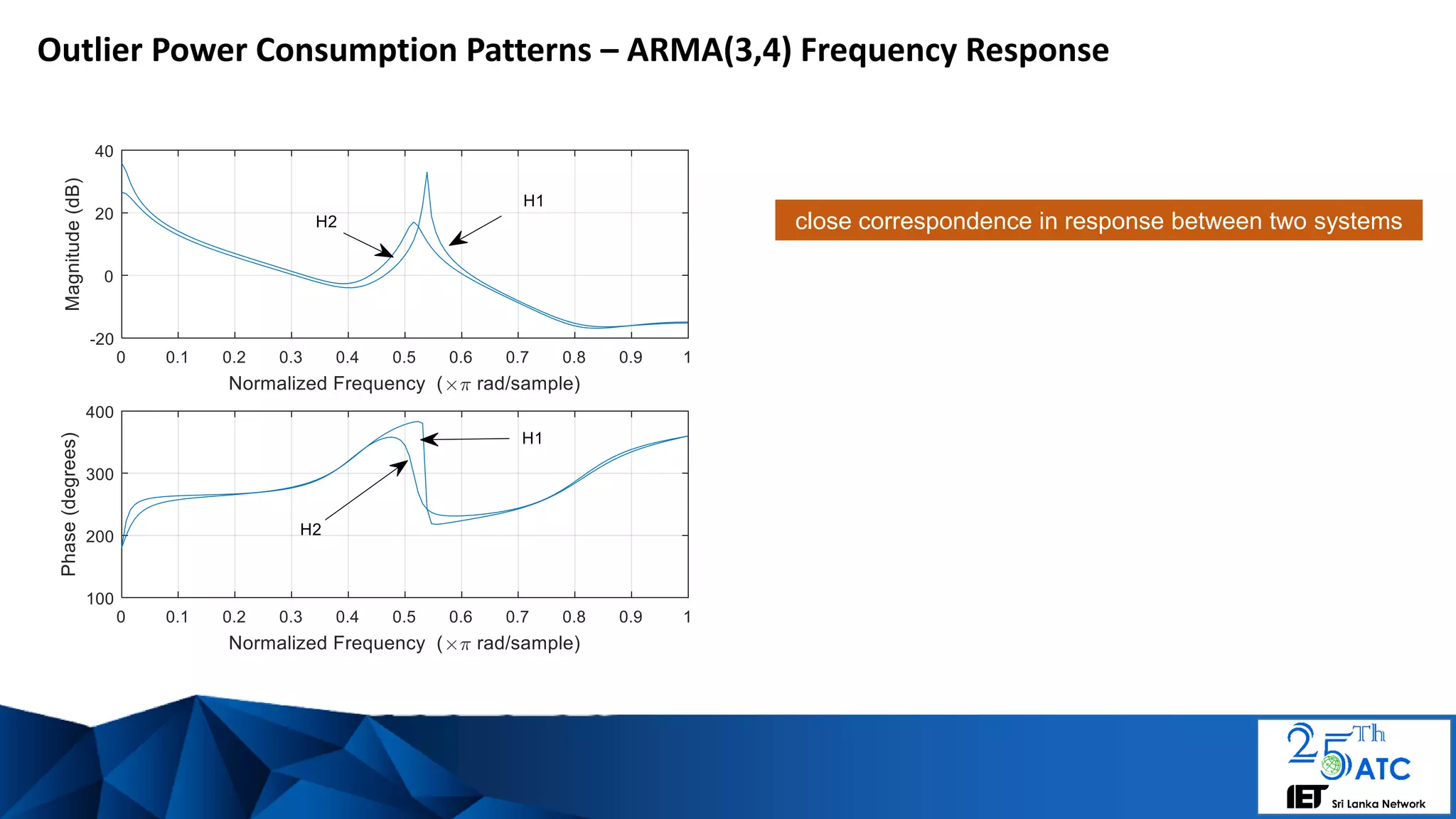
14. Outlier Power Consumption Patterns of Complexity ARMA(3,4)
Params: a1 a2 a3 1 b1 b2 b3 b4 ]
[H1 #26: 0.8369 -0.7429 1.0646 1 0.8309 0.6752 0.5491 0.3363]
[H2 #60: 0.9325 -0.8261 0.9477 1 0.8137 0.6589 0.5539 0.3765]
Close match between
ARMA parameters sets

15. Outlier Power Consumption Patterns – ARMA(3,4) Frequency Response
close correspondence in response between two systems

16. Expected Temporal Behavior of Price Elasticity of Demand for Electricity
Electricity Demand a time varying function
Time of Day (Hrs)
KW
Greater inelasticity expected near peak demand
Away from peak
Nearer peak
P1
Price Elasticity of Demand should vary with time of day, segment, demographics, location …

17. Peak Demand Pattern & Price Elasticity of Demand
Determine change in Price needed to effect a change in Quantity Demanded
Identify Peak Demand and Energy consumption to moderate demand
Time of Day (Hrs)
KW

18. Demand Modification Strategy
Modified DemandPeak Consumption Pattern
Time of Day (Hrs)
KW
Demand increases on either side of peak with lower pricesPrice increases with demand
Amount consumed drops with increasing price Amount consumed increases with lower prices
KW

19. Conclusion
• Power patterns can be grouped by modeling as the result of an ARMA random process
• Such groups exhibit fairly close correspondence in both time and frequency behavior
• Strategies that take advantage of the group consumption pattern can be devised
• Dynamic pricing strategies can be implemented to moderate the peak and even the load
• Unique strategies can be devised catering to specific patterns (groups) of usage
• Outlier power patterns can be detected providing insights to anomalous consumption behavior

20. THANK YOU