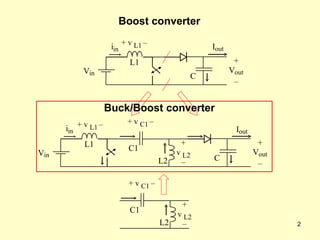
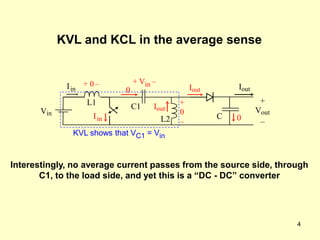
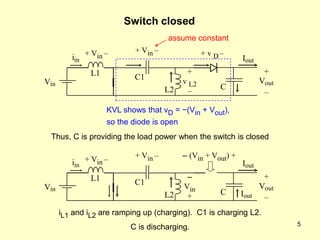
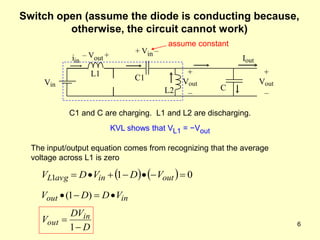
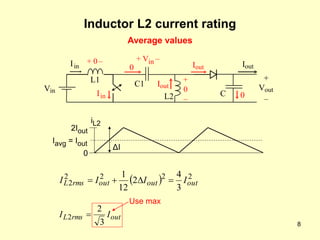
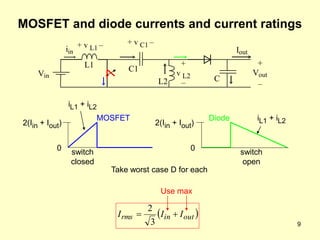
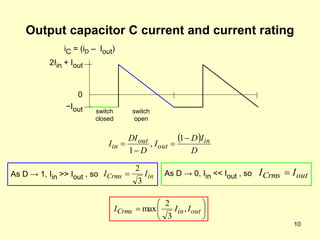
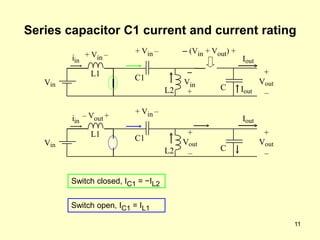
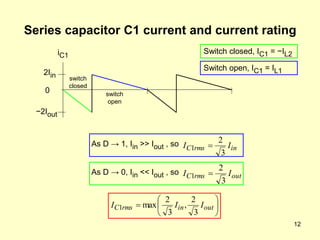
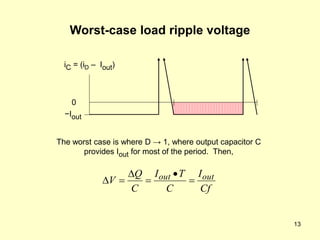
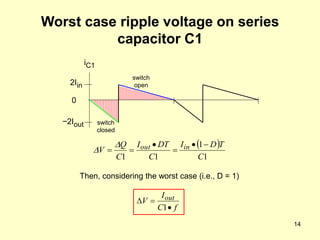
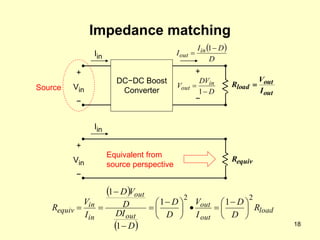
The document describes the operation and design considerations of a buck/boost DC-DC converter circuit. It provides equations to calculate component ratings for the input inductor, output capacitor, MOSFET, diode, and other parts. Design examples are given to illustrate how to select appropriate component values and ratings to ensure continuous inductor currents and minimize output voltage ripple.

1. 1
EE462L, Fall 2011
DC−DC Buck/Boost Converter

2. 2
Boost converter
+
Vout
–
Iout
C
Vin
iin
L1
+ v L1 –
Buck/Boost converter
+
v L2
–
C1
+ v C1 –
L2
Vin
iin
L1
+ v L1 –
+
v L2
–
C1
+ v C1 –
L2
+
Vout
–
Iout
C

3. 3
Buck/Boost converter
This circuit is more unforgiving than the boost converter, because the
MOSFET and diode voltages and currents are higher
• Before applying power, make sure that your D is at
the minimum, and that a load is solidly connected
• Limit your output voltage to 90V
Vin
iin
L1
+ v L1 –
+
v L2
–
C1
+ v C1 –
L2
+
Vout
–
Iout
C

4. 4
+
Vout
–
Iout
C
Vin
Iin
L1
+ 0 –
+
0
–
KVL and KCL in the average sense
0
0
Iout
Iin
C1
L2
Iout
+ Vin –
KVL shows that VC1 = Vin
Interestingly, no average current passes from the source side, through
C1, to the load side, and yet this is a “DC - DC” converter

5. 5
Switch closed
Vin
iin
L1
+ Vin –
+
v L2
–
C1
+ Vin –
L2
+
Vout
–
Iout
C
assume constant
+ v D –
KVL shows that vD = −(Vin + Vout),
so the diode is open
Thus, C is providing the load power when the switch is closed
Vin
iin
L1 –
Vin
+
C1
+ Vin –
L2
+
Vout
–
Iout
C
– (Vin + Vout) +
Iout
iL1 and iL2 are ramping up (charging). C1 is charging L2.
C is discharging.
+ Vin –

6. 6
Switch open (assume the diode is conducting because,
otherwise, the circuit cannot work)
Vin
iin
L1
– Vout +
C1
+ Vin –
L2
+
Vout
–
Iout
C
C1 and C are charging. L1 and L2 are discharging.
+
Vout
–
KVL shows that VL1 = −Vout
    0
1
1 





 out
in
avg
L V
D
V
D
V
in
out V
D
D
V 


 )
1
(
D
DV
V in
out


1
The input/output equation comes from recognizing that the average
voltage across L1 is zero
assume constant

7. 7
Inductor L1 current rating
in
rms
L I
I
3
2
1 
Use max
During the “on” state, L1 operates under the same conditions
as the boost converter L, so the results are the same

8. 8
Inductor L2 current rating
  2
2
2
2
2
3
4
2
12
1
out
out
out
rms
L I
I
I
I 



out
rms
L I
I
3
2
2 
2Iout
0
Iavg = Iout
ΔI
iL2
Use max
+
Vout
–
Iout
C
Vin
Iin
L1
+ 0 –
+
0
–
0
0
Iout
Iin
C1
L2
Iout
+ Vin –
Average values

9. 9
MOSFET and diode currents and current ratings
0
2(Iin + Iout)
0
Take worst case D for each
Vin
iin
L1
+ v L1 –
+
v L2
–
C1
+ v C1 –
L2
+
Vout
–
Iout
C
MOSFET Diode iL1 + iL2
 
out
in
rms I
I
I 

3
2
Use max
switch
closed
switch
open
2(Iin + Iout)
iL1 + iL2

10. 10
Output capacitor C current and current rating
in
Crms I
I
3
2
 out
Crms I
I 
2Iin + Iout
−Iout
0
As D → 1, Iin >> Iout , so
iC = (iD – Iout)
As D → 0, Iin << Iout , so
 
D
I
D
I
D
DI
I in
out
out
in




1
,
1






 out
in
Crms I
I
I ,
3
2
max
switch
closed
switch
open

11. 11
Series capacitor C1 current and current rating
Switch closed, IC1 = −IL2
Vin
iin
L1 –
Vin
+
C1
+ Vin –
L2
+
Vout
–
Iout
C
– (Vin + Vout) +
Iout
+ Vin –
Vin
iin
L1
– Vout +
C1
+ Vin –
L2
+
Vout
–
Iout
C
+
Vout
–
Switch open, IC1 = IL1

12. 12
Series capacitor C1 current and current rating
in
rms
C I
I
3
2
1 
2Iin
−2Iout
0
As D → 1, Iin >> Iout , so
iC1
As D → 0, Iin << Iout , so






 out
in
rms
C I
I
I
3
2
,
3
2
max
1
switch
closed
switch
open
out
rms
C I
I
3
2
1 
Switch closed, IC1 = −IL2
Switch open, IC1 = IL1

13. 13
Worst-case load ripple voltage
Cf
I
C
T
I
C
Q
V out
out 





The worst case is where D → 1, where output capacitor C
provides Iout for most of the period. Then,
−Iout
0
iC = (iD – Iout)

14. 14
Worst case ripple voltage on series
capacitor C1
2Iin
−2Iout
0
iC1
f
C
I
V out



1
switch
closed
switch
open
 
1
1
1
1 C
T
D
I
C
DT
I
C
Q
V in
out 







Then, considering the worst case (i.e., D = 1)

15. 15
Voltage ratings
MOSFET and diode see (Vin + Vout)
• Diode and MOSFET, use 2(Vin + Vout)
• Capacitor C1, use 1.5Vin
• Capacitor C, use 1.5Vout
Vin
L1 C1
+ Vin –
L2
+
Vout
–
C
– (Vin + Vout) +
Vin
L1
– Vout +
C1
+ Vin –
L2
+
Vout
–
C

16. 16
Continuous current in L1
sec
/
1
A
L
Vout

   
f
L
D
V
T
D
L
D
DV
T
D
L
V
I
boundary
in
boundary
in
boundary
out
in
1
1
1
1
1
1
2 







f
I
D
V
L
in
in
boundary
2
1 
2Iin
0
Iavg = Iin
iL
(1 − D)T
f
I
V
L
in
in
2
1 guarantees continuous conduction
Then, considering the worst case (i.e., D → 1),
use max
use min

17. 17
Continuous current in L2
sec
/
2
A
L
Vout

f
L
D
V
T
D
L
V
I
boundary
out
boundary
out
out
2
)
1
(
)
1
(
2
2





2Iout
0
Iavg = Iout
iL
(1 − D)T
f
I
D
V
L
out
out
boundary
2
)
1
(
2


f
I
V
L
out
out
2
2  guarantees continuous conduction
Then, considering the worst case (i.e., D → 0),
use max
use min

18. 18
Impedance matching
out
out
load
I
V
R 
equiv
R
 
 
load
out
out
out
out
in
in
equiv R
D
D
I
V
D
D
D
DI
D
V
D
I
V
R
2
2
1
1
1
1





 







 





DC−DC Boost
Converter
+
Vin
−
+
−
Iin
+
Vin
−
Iin
Equivalent from
source perspective
Source D
DV
V in
out


1
 
D
D
I
I in
out


1

19. 19
Impedance matching
 
 
load
out
out
out
out
in
in
equiv R
D
D
I
V
D
D
D
DI
D
V
D
I
V
R
2
2
1
1
1
1





 







 





For any Rload, as D → 0, then Requiv → ∞ (i.e., an open circuit)
For any Rload, as D → 1, then Requiv → 0 (i.e., a short circuit)
Thus, the buck/boost converter can sweep the entire I-V
curve of a solar panel

20. 20
Example - connect a 100Ω load resistor
PV Station 13, Bright Sun, Dec. 6, 2002
0
1
2
3
4
5
6
0 5 10 15 20 25 30 35 40 45
V(panel) - volts
I
-
amps
D = 0.80
D = 0.50
D = 0.88
With a 100Ω load resistor attached, raising D from 0 to 1 moves the solar
panel load from the open circuit condition to the short circuit condition

21. 21
Example - connect a 5Ω load resistor
PV Station 13, Bright Sun, Dec. 6, 2002
0
1
2
3
4
5
6
0 5 10 15 20 25 30 35 40 45
V(panel) - volts
I
-
amps
D = 0.47
D = 0.18
D = 0.61

22. 22
Worst-Case Component Ratings Comparisons
for DC-DC Converters
Converter
Type
Input Inductor
Current
(Arms)
Output
Capacitor
Voltage
Output Capacitor
Current (Arms)
Diode and
MOSFET
Voltage
Diode and
MOSFET
Current
(Arms)
Buck/Boost
in
I
3
2 1.5 out
V






out
in I
I ,
3
2
max
)
(
2 out
in V
V 
 
out
in I
I 
3
2
5.66A p-p 200V, 250V 16A, 20A
Our components
9A 250V
10A, 5A
10A 90V 40V, 90V
Likely worst-case buck/boost situation
10A, 5A
MOSFET M. 250V, 20A
L1. 100µH, 9A
C. 1500µF, 250V, 5.66A p-p
Diode D. 200V, 16A
L2. 100µH, 9A
C1. 33µF, 50V, 14A p-p
BUCK/BOOST DESIGN

23. 23
Comparisons of Output Capacitor Ripple Voltage
Converter Type Volts (peak-to-peak)
Buck/Boost
Cf
Iout 5A
1500µF 50kHz
0.067V
MOSFET M. 250V, 20A
L1. 100µH, 9A
C. 1500µF, 250V, 5.66A p-p
Diode D. 200V, 16A
L2. 100µH, 9A
C1. 33µF, 50V, 14A p-p
BUCK/BOOST DESIGN

24. 24
Minimum Inductance Values Needed to
Guarantee Continuous Current
Converter Type For Continuous
Current in the Input
Inductor
For Continuous
Current in L2
Buck/Boost
f
I
V
L
in
in
2
1 
f
I
V
L
out
out
2
2 
40V
2A 50kHz
200µH
90V
2A 50kHz
450µH
MOSFET M. 250V, 20A
L1. 100µH, 9A
C. 1500µF, 250V, 5.66A p-p
Diode D. 200V, 16A
L2. 100µH, 9A
C1. 33µF, 50V, 14A p-p
BUCK/BOOST DESIGN

25. 25
Additional Components for Buck/Boost Converter
Series Capacitor
Voltage
Series Capacitor (C1)
Current (Arms)
Series
Capacitor (C1)
Ripple Voltage
(peak-to-peak)
Second
Inductor (L2)
Current (Arms)
1.5 in
V








out
in I
I
3
2
,
3
2
max
f
C
Iout
1
out
I
3
2
MOSFET M. 250V, 20A
L1. 100µH, 9A
C. 1500µF, 250V, 5.66A p-p
Diode D. 200V, 16A
L2. 100µH, 9A
C1. 33µF, 50V, 14A p-p
10A 5A
40V
Likely worst-case buck/boost situation
5A
5A
33µF 50kHz
3.0V
BUCK/BOOST DESIGN
Our components 9A
14A p-p
50V
Conclusion - 50kHz may be too low
for buck/boost converter

26. 26
Worst-Case Component Ratings Comparisons for DC-DC Converters
Converter
Type
Input Inductor
Current (Arms)
Output
Capacitor
Voltage
Output Capacitor
Current (Arms)
Diode and
MOSFET Voltage
Diode and
MOSFET
Current (Arms)
Buck
out
I
3
2 1.5 out
V
out
I
3
1 2 in
V
out
I
3
2
Boost
in
I
3
2 1.5 out
V out
I 2 out
V
in
I
3
2
Buck/Boost
in
I
3
2 1.5 out
V








out
in I
I ,
3
2
max
 
out
in V
V 
2
 
out
in I
I 
3
2
Additional Components for Buck/Boost Converter
Series Capacitor
Voltage
Series Capacitor (C1)
Current (Arms)
Series Capacitor
(C1) Ripple
Voltage (peak-to-
peak)
Second Inductor
(L2) Current
(Arms)
1.5 in
V








out
in I
I
3
2
,
3
2
max
f
C
Iout
1
out
I
3
2

27. 27
Comparisons of Output Capacitor Ripple Voltage
Converter Type Volts (peak-to-peak)
Buck
Cf
Iout
4
Boost
Cf
Iout
Buck/Boost
Cf
Iout
Minimum Inductance Values Needed to Guarantee Continuous Current
Converter Type For Continuous Current
in the Input Inductor
For Continuous
Current in L2
Buck
f
I
V
L
out
out
2
 –
Boost
f
I
V
L
in
in
2
 –
Buck/Boost
f
I
V
L
in
in
2
1 
f
I
V
L
out
out
2
2 