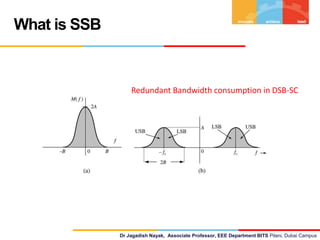
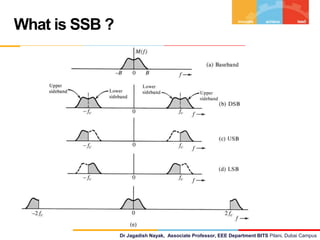
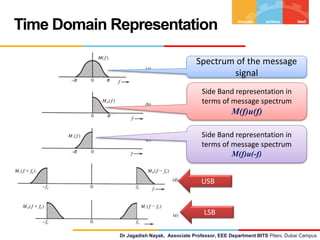
The document discusses Single Side Band (SSB) modulation and demodulation, focusing on its theory and mathematical representation. It covers the importance of signum and Hilbert transforms in SSB, outlining how they aid in time and frequency domain manipulations. Additionally, it presents the time domain representations and spectrum expressions for both upper and lower sidebands.

1. BITS Pilani
Dubai Campus
Communication
Systems
(EEE/ECE F311)
Dr T G Thomas & Dr Jagadish Nayak

2. BITS Pilani
Dubai Campus
Single Side Band (SSB) Modulation
and Demodulation

3. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
What is SSB
Redundant Bandwidth consumption in DSB-SC

4. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
What is SSB ?

5. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
Time Domain Representation
Spectrum of the message
signal
Side Band representation in
terms of message spectrum
M(f)u(f)
Side Band representation in
terms of message spectrum
M(f)u(-f)
USB
LSB

6. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
• Let and are Fourier
Transform Pairs.
• Moreover
• We can write
• Where mh(t) is unknown
Time Domain Representation
)
(
)
( t
m
f
M 
  )
(
)
( t
m
f
M 
 
)
(
)
(
)
(
)
(
)
(
)
(
t
m
t
m
t
m
f
M
f
M
f
M








 
 
)
(
)
(
2
1
)
(
)
(
)
(
2
1
)
(
t
jm
t
m
t
m
and
t
jm
t
m
t
m
h
h







7. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
We know that
• The above equation can be written in terms of signum
function.
• Signum function is given by
Time Domain Representation
)
(
)
(
)
( f
u
f
M
f
M 

 
)
sgn(
)
(
2
1
)
(
2
1
)
sgn(
1
)
(
2
1
)
(
f
f
M
f
M
f
f
M
f
M






8. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
• Compare
• We get
• Hence we can write
From the Fourier transform table , we can find that
Appling above result , we get
Time Domain Representation
&
)
sgn(
)
(
2
1
)
(
2
1
)
( f
f
M
f
M
f
M 

  
)
(
)
(
2
1
)
( t
jm
t
m
t
m h



)
sgn(
)
(
)
( f
f
M
t
jmh 
)
sgn(
)
(
)
( f
f
jM
f
Mh 

)
sgn(
1
f
j
t



t
f
M
f
Mh

1
)
(
)
( 

9. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
• We know that multiplication in the frequency domain is
equivalent to convolution in time domain. Using this we
can write.
• We can say
Time Domain Representation




d
t
m
t
mh 





)
(
1
)
( Hilbert Transform of m(t)
)
(
of
Transform
Hilbert
)
( t
m
t
mh 
H(f)=-jsgn(f)
M(f) Mh(f)
m(t) mh(t)













0
.
1
0
.
1
)
(
2
2
f
e
j
f
e
j
f
H
where
j
j



10. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
Time Domain Representation
We can observe from above that if we delay the phase of every
component by π/2 without changing the amplitude, we get mh(t),
which is the Hilbert transform of m(t)
So Hilbert Transformer is an ideal phase shifter , that shifts the
phase of every component by - π/2

11. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
• Now we can express SSB in terms of m(t) and mh(t)
USB spectrum can be expressed as
The Inverse transform of above equation is
Using
We can write
Time Domain Representation
)
(
)
(
)
( c
c
USB f
f
M
f
f
M
f 


 


t
f
j
t
f
j
USB
c
c
e
t
m
e
t
m
t 

 2
2
)
(
)
(
)
( 

 

 
 
)
(
)
(
2
1
)
(
)
(
)
(
2
1
)
(
t
jm
t
m
t
m
and
t
jm
t
m
t
m
h
h






)
2
sin(
)
(
)
2
cos(
)
(
)
( t
f
t
m
t
f
t
m
t c
h
c
USB 

 


12. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
Using similar process, we can also show that
Hence the general SSB equation is given by
Time Domain Representation
)
2
sin(
)
(
)
2
cos(
)
(
)
( t
f
t
m
t
f
t
m
t c
h
c
LSB 

 

)
2
sin(
)
(
)
2
cos(
)
(
)
( t
f
t
m
t
f
t
m
t c
h
c
SSB 

 


13. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
Find
If m(t)=cos(2πfmt)
We know that mh(t) is the delaying m(t) by π/2
Tone Modulation : SSB
)
2
sin(
)
(
)
2
cos(
)
(
)
( t
f
t
m
t
f
t
m
t c
h
c
SSB 

 

t
f
f
t
f
t
f
t
f
t
f
t
t
f
t
f
t
m
m
c
c
m
c
m
SSB
m
m
h
)
(
2
cos
)
2
sin(
)
2
sin(
)
2
cos(
)
2
cos(
)
(
)
2
sin(
)
2
2
cos(
)
(

















14. Dr Jagadish Nayak, Associate Professor, EEE Department BITS Pilani, Dubai Campus
Tone Modulation : SSB