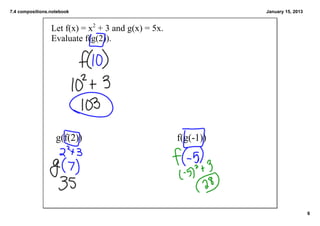
The document discusses function composition and states some key rules: compositions are evaluated from the innermost function outwards; denominators cannot be zero and radicands cannot be negative. It provides examples of finding the compositions h(x) of various functions f(x) and g(x), and evaluating compositions like f(g(2)) at different values. The domain for compositions is also discussed.

1. 7.4 compositions.notebook January 15, 2013
Domain Restrictions
Denominator can't be zero
Radicand can't be negative
1

2. 7.4 compositions.notebook January 15, 2013
Let f(x) = 4x2 and g(x) = x + 1. Find h(x) and state its domain.
h(x) = f(x) + g(x) h(x) = f(x) ­ g(x)
2

3. 7.4 compositions.notebook January 15, 2013
Let f(x) = x3 and g(x) = 2x. Find h(x) and state its domain.
f(x)
h(x) = f(x) g(x) h(x) =
g(x)
3

4. 7.4 compositions.notebook January 15, 2013
Composition work from the inside out
f(g(x)) read: f at g at x
f(x) = 5x ­1
g(x) = 2 + x2
f(g(x)) g(f(x))
4

5. 7.4 compositions.notebook January 15, 2013
Let f(x) = x2 and g(x) = 2x + 3
f(g(x)) g(f(x))
State the Domain
5

6. 7.4 compositions.notebook January 15, 2013
Let f(x) = x2 + 3 and g(x) = 5x.
Evaluate f(g(2)).
g(f(2)) f(g(­1))
6