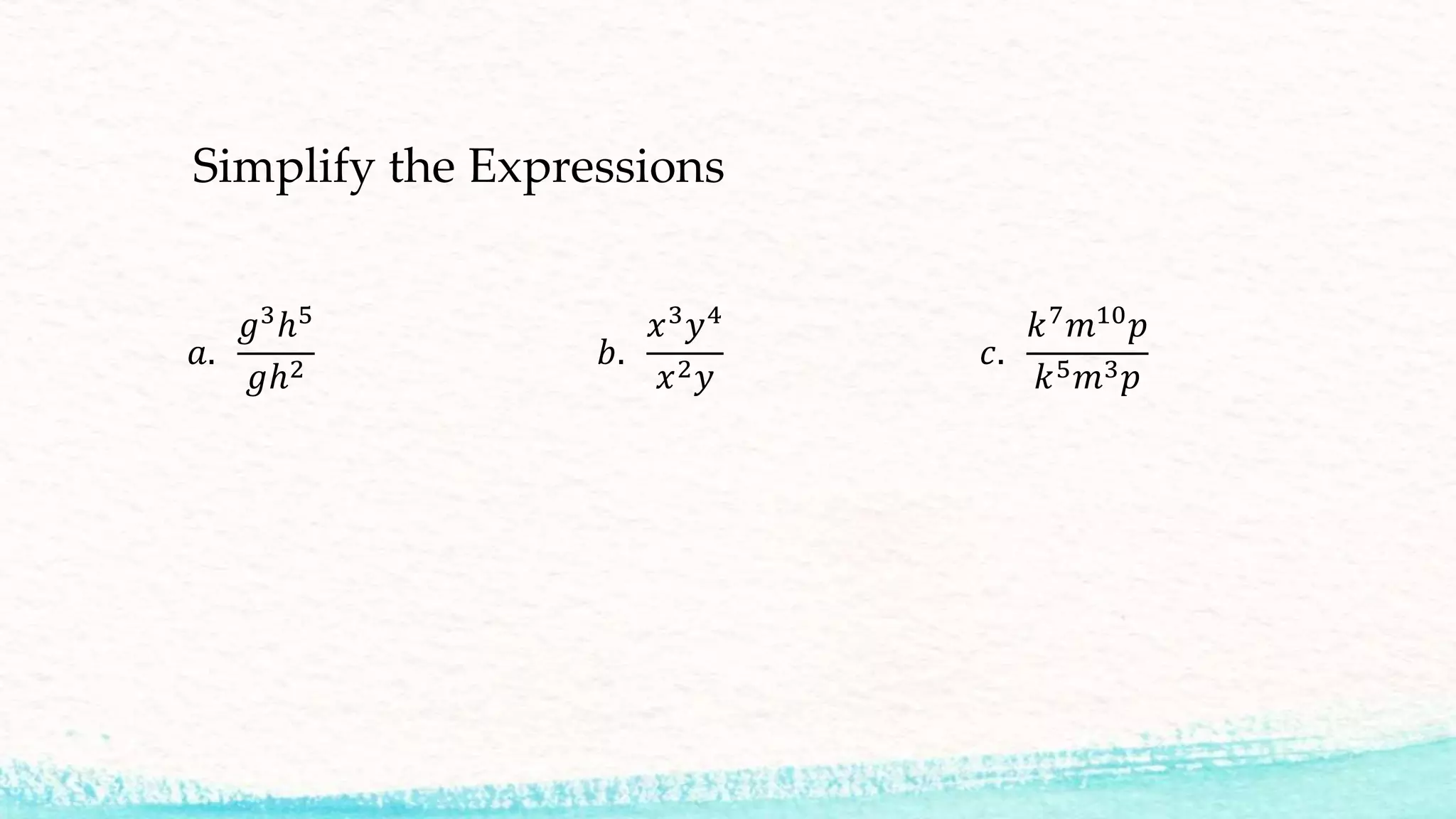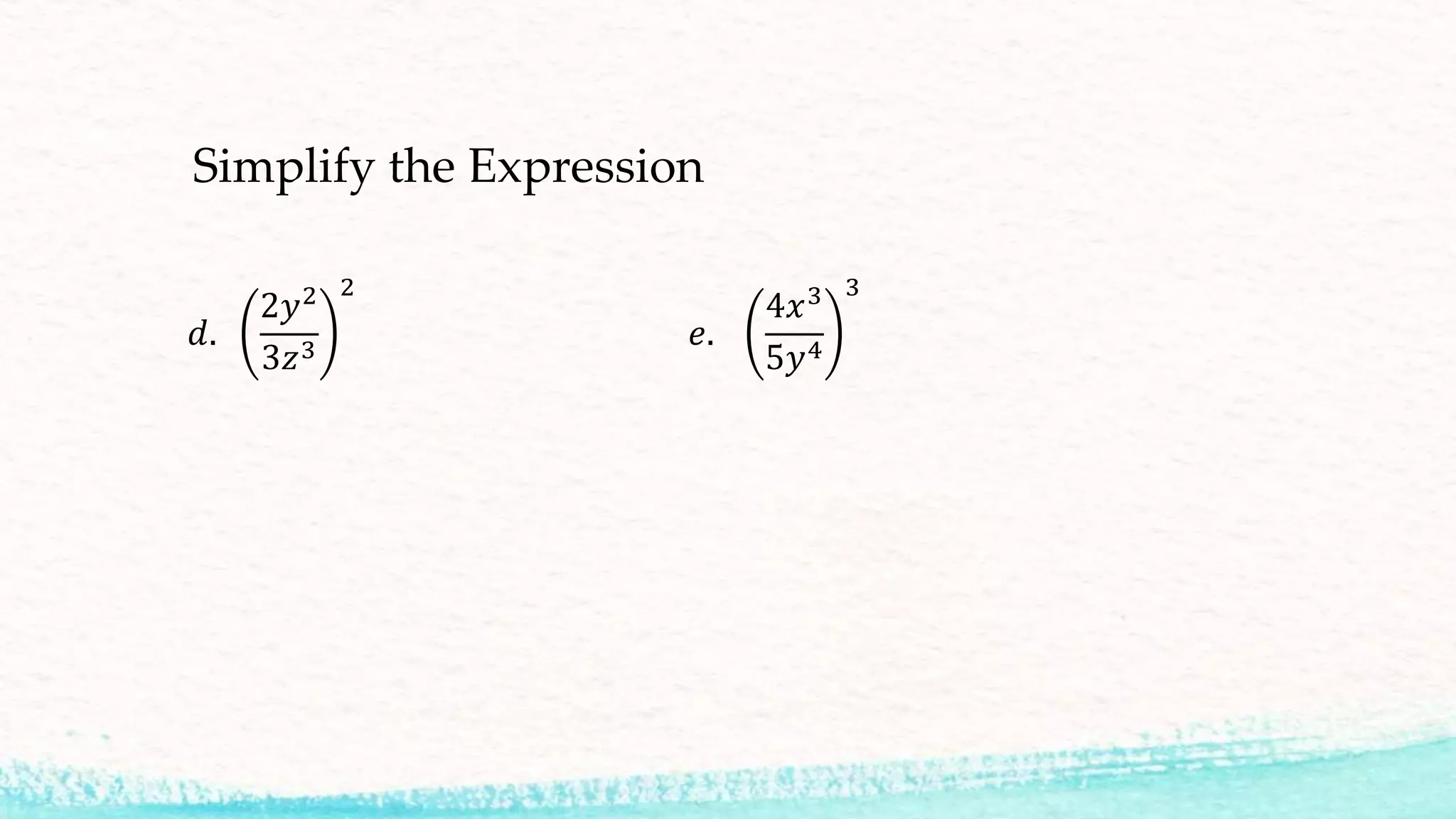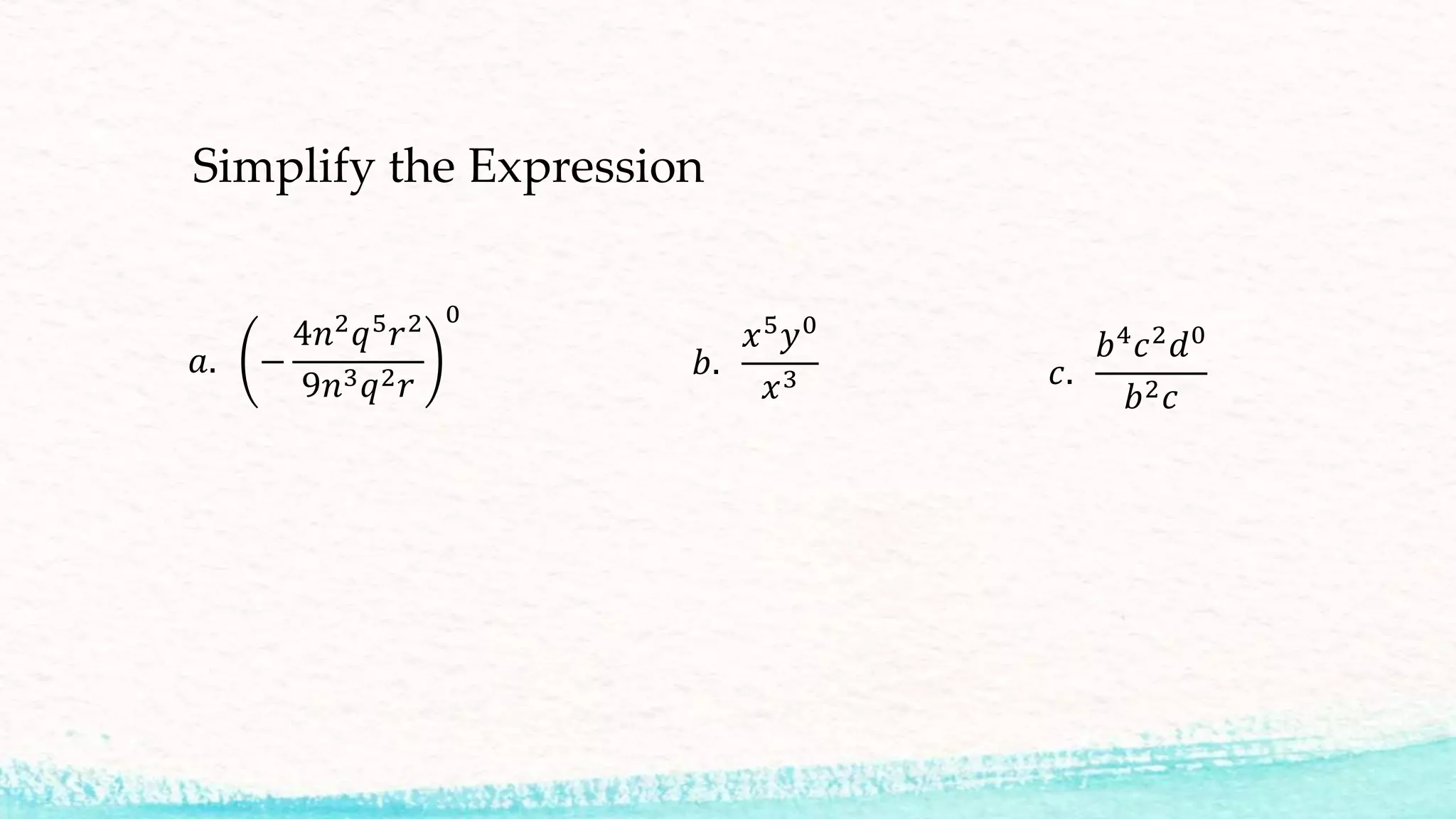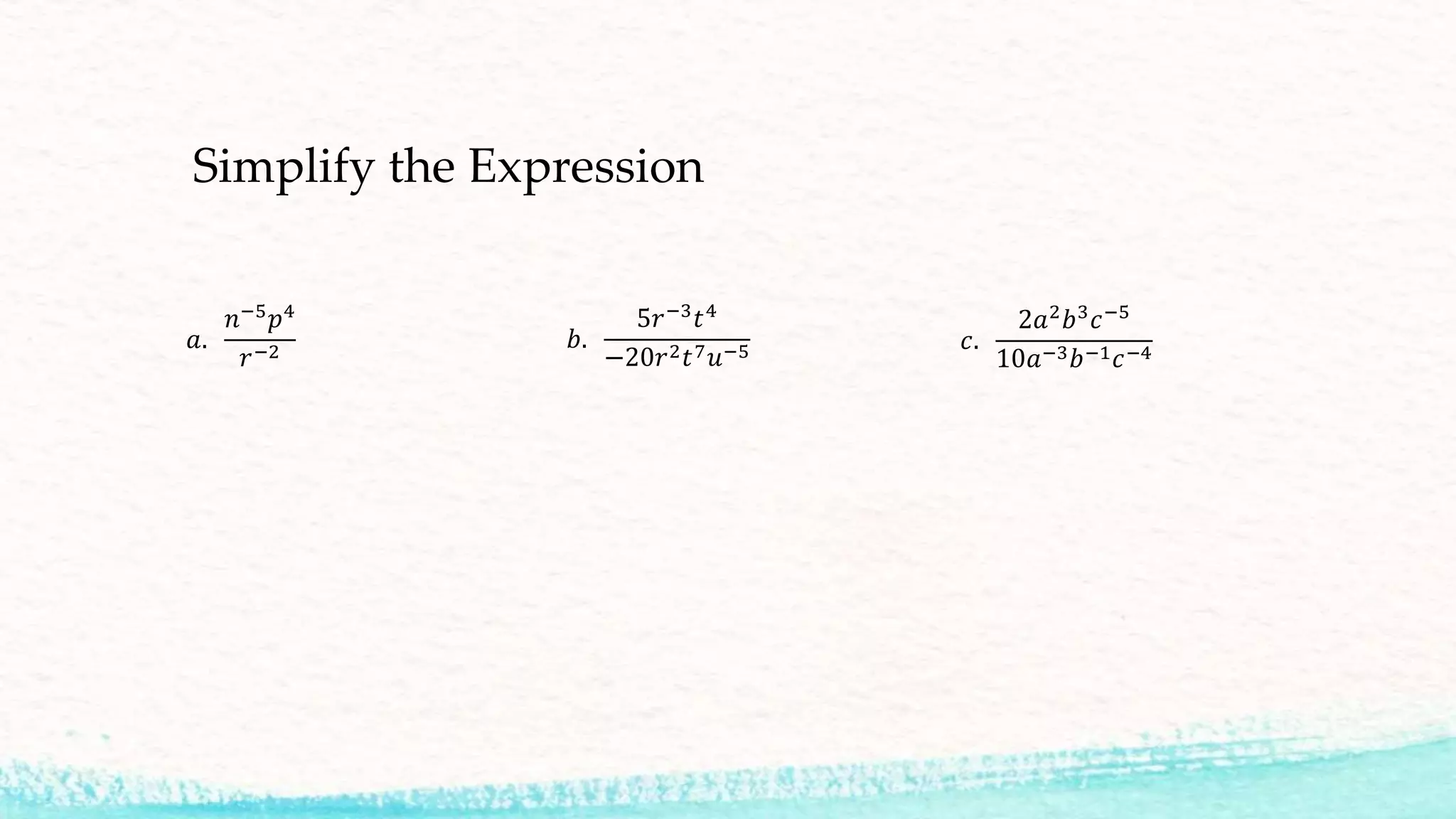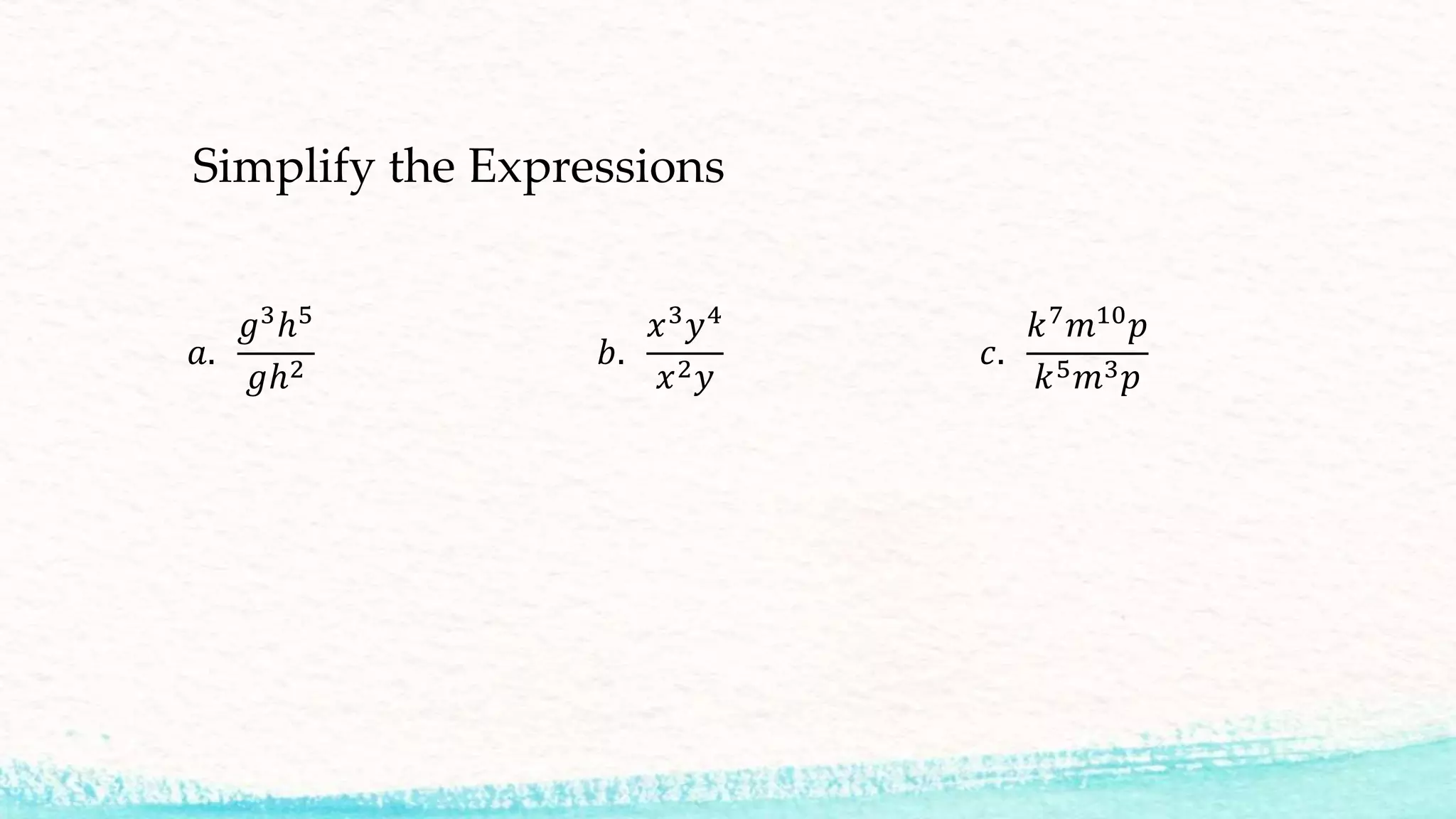
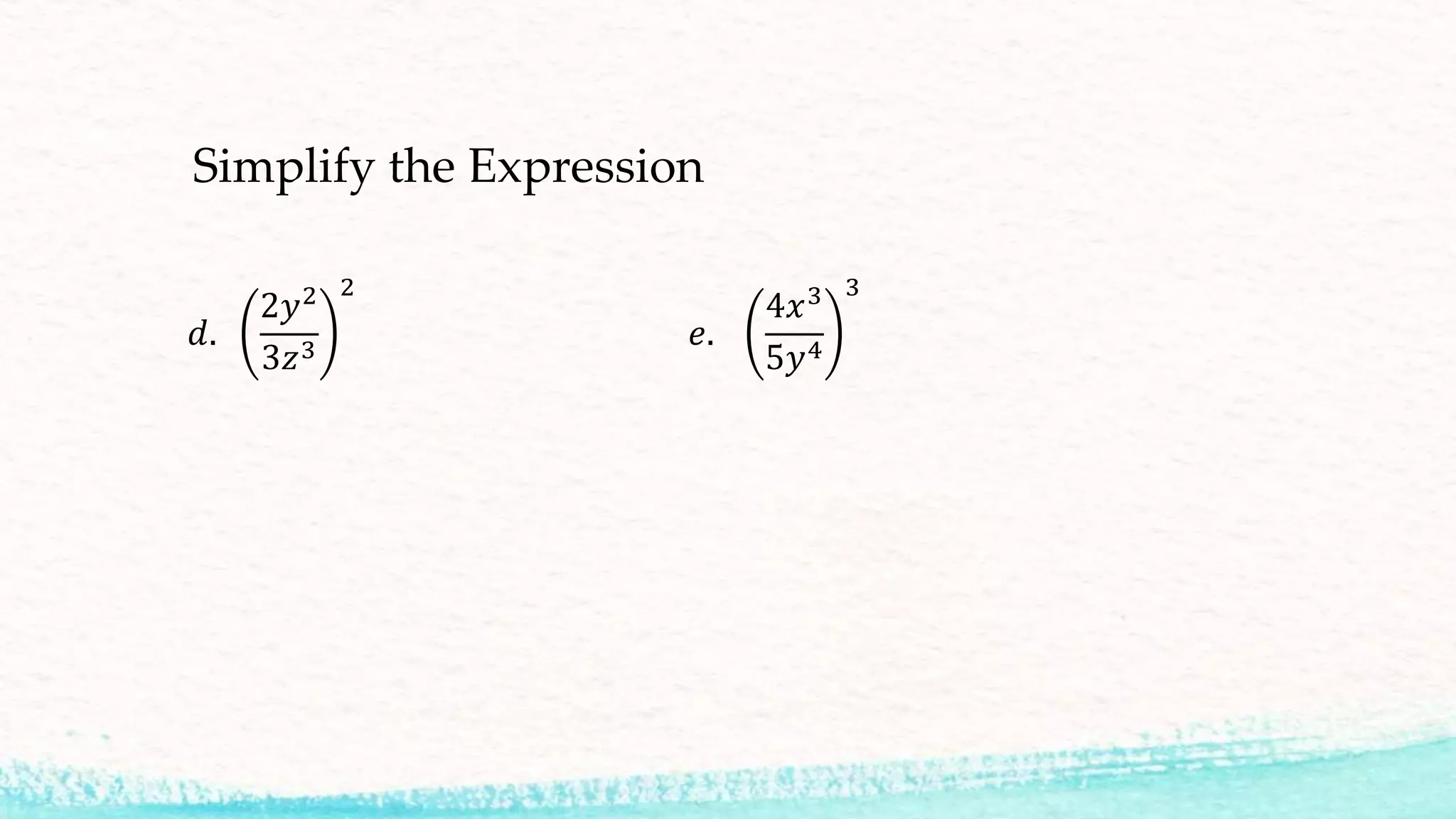
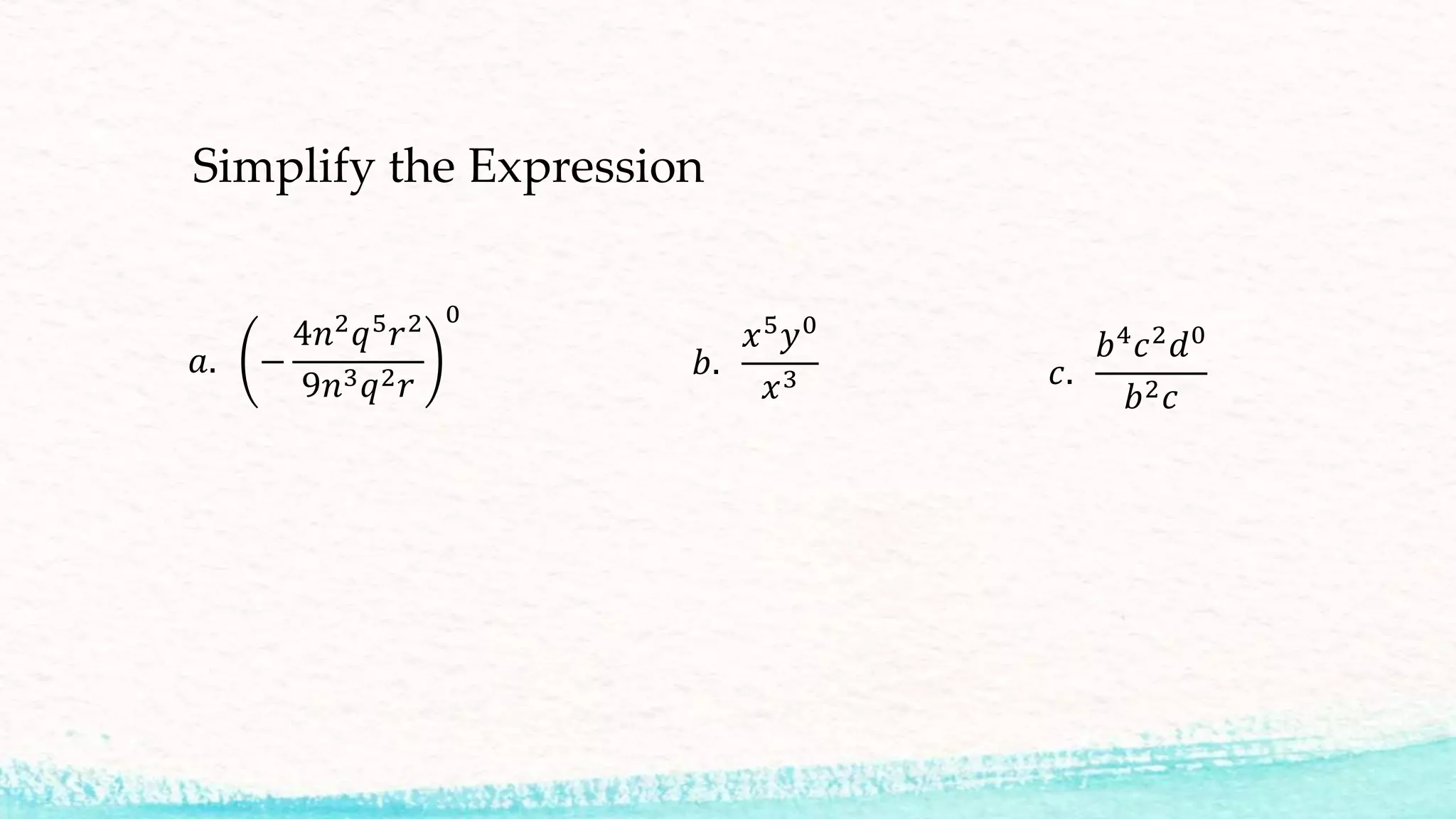
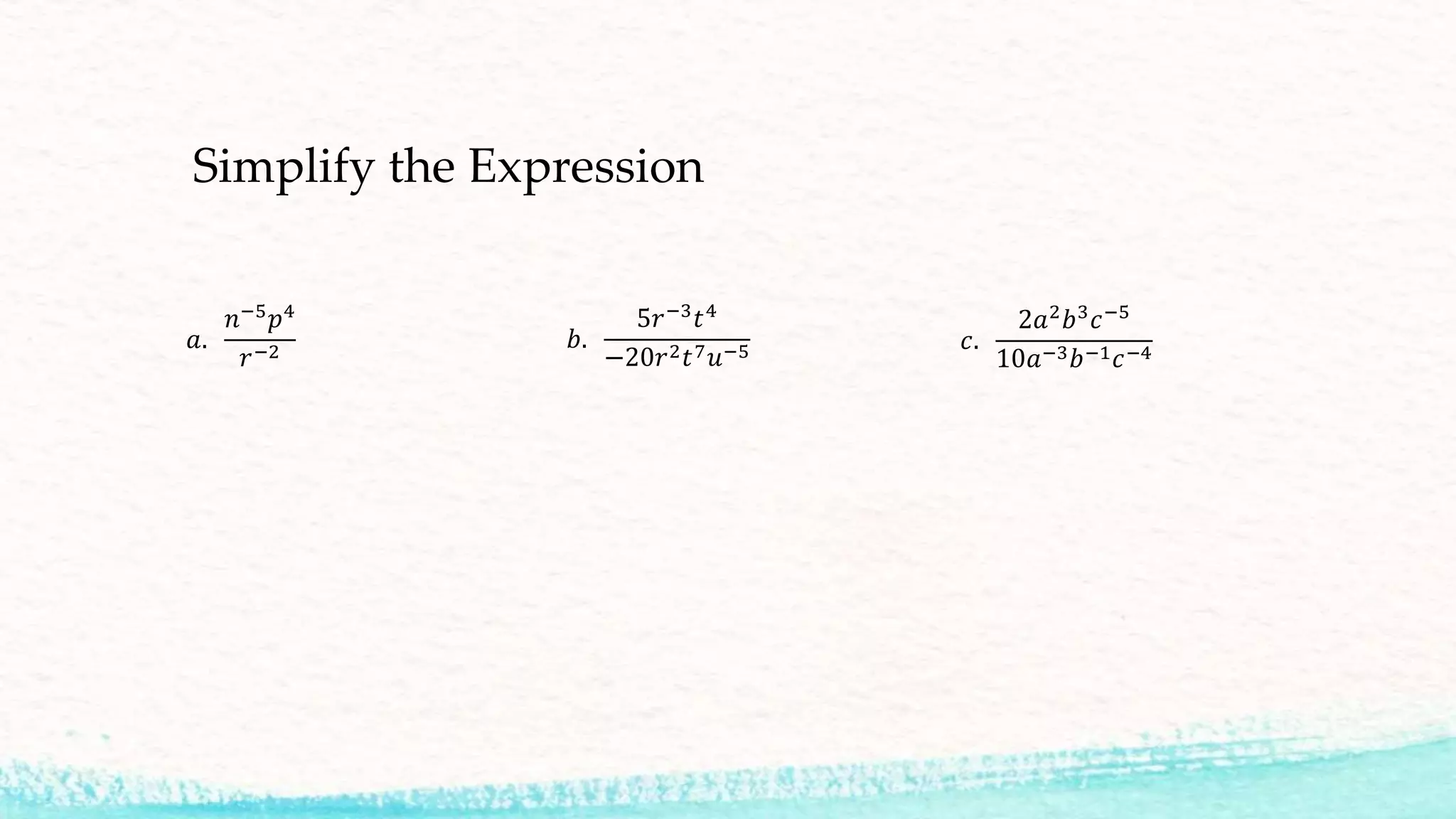
This document discusses several properties of exponents that can be used to simplify expressions involving exponents. It covers: 1) Quotient of powers - subtracting exponents when dividing terms with the same base. 2) Power of a quotient - finding the power of a term when the base is a fraction, by finding the powers of the numerator and denominator. 3) Zero exponent property - any number to the zero power is equal to 1. 4) Negative exponent property - a negative exponent is the same as the reciprocal of the positive exponent. 5) Several examples of simplifying expressions using these properties are provided.

1. Division Properties of
Exponents
Section 7.2 pages 398-405

2. Quotient of Powers
To divide two powers with the same base, subtract the exponents.
𝑐5
𝑐2
= 𝑐5−2 = 𝑐3

3. Simplify the Expressions
𝑎.
𝑔3ℎ5
𝑔ℎ2
𝑏.
𝑥3 𝑦4
𝑥2 𝑦
𝑐.
𝑘7 𝑚10 𝑝
𝑘5 𝑚3 𝑝

4. Power of a Quotient
To find the power of a quotient, find the power of the numerator and the power of the denominator.
3
5
4
=
34
54
=
81
625

5. Simplify the Expressions
𝑎.
3𝑝3
7
2
𝑏.
3𝑥4
4
3
𝑐.
5𝑥5
𝑦
6
2

6. Simplify the Expression
𝑑.
2𝑦2
3𝑧3
2
𝑒.
4𝑥3
5𝑦4
3

7. Zero Exponent Property
Any number raised to the zero power is equal to 1.
150 = 1
2
7
0
= 1

8. Simplify the Expression
𝑎. −
4𝑛2 𝑞5 𝑟2
9𝑛3 𝑞2 𝑟
0
𝑏.
𝑥5
𝑦0
𝑥3 𝑐.
𝑏4
𝑐2
𝑑0
𝑏2 𝑐

9. Negative Exponent Property
For any nonzero number a and any integer n, 𝑎−𝑛
is the reciprocal of 𝑎 𝑛
. Also, the reciprocal of 𝑎−𝑛
is 𝑎 𝑛
.
𝑥−2 =
1
𝑥2
1
𝑥−2
= 𝑥2
Negative exponent means that base is on the wrong side of the fraction bar.
When you put the base on the correct side of the fraction bar the power
becomes positive because now it belongs.

10. Simplify the Expression
𝑎.
𝑛−5 𝑝4
𝑟−2
𝑏.
5𝑟−3
𝑡4
−20𝑟2 𝑡7 𝑢−5 𝑐.
2𝑎2 𝑏3 𝑐−5
10𝑎−3 𝑏−1 𝑐−4

11. Simplify the Expressions
𝑑.
32𝑎−8
𝑏3
𝑐−4
4𝑎3 𝑏5 𝑐−2 𝑒.
5𝑗−3
𝑘2
𝑚−6
25𝑘−4 𝑚−2
𝑓.
𝑤𝑦−6
𝑣−3 𝑤𝑥2
−1

12. Homework
Page 403 #19-42, 45-56