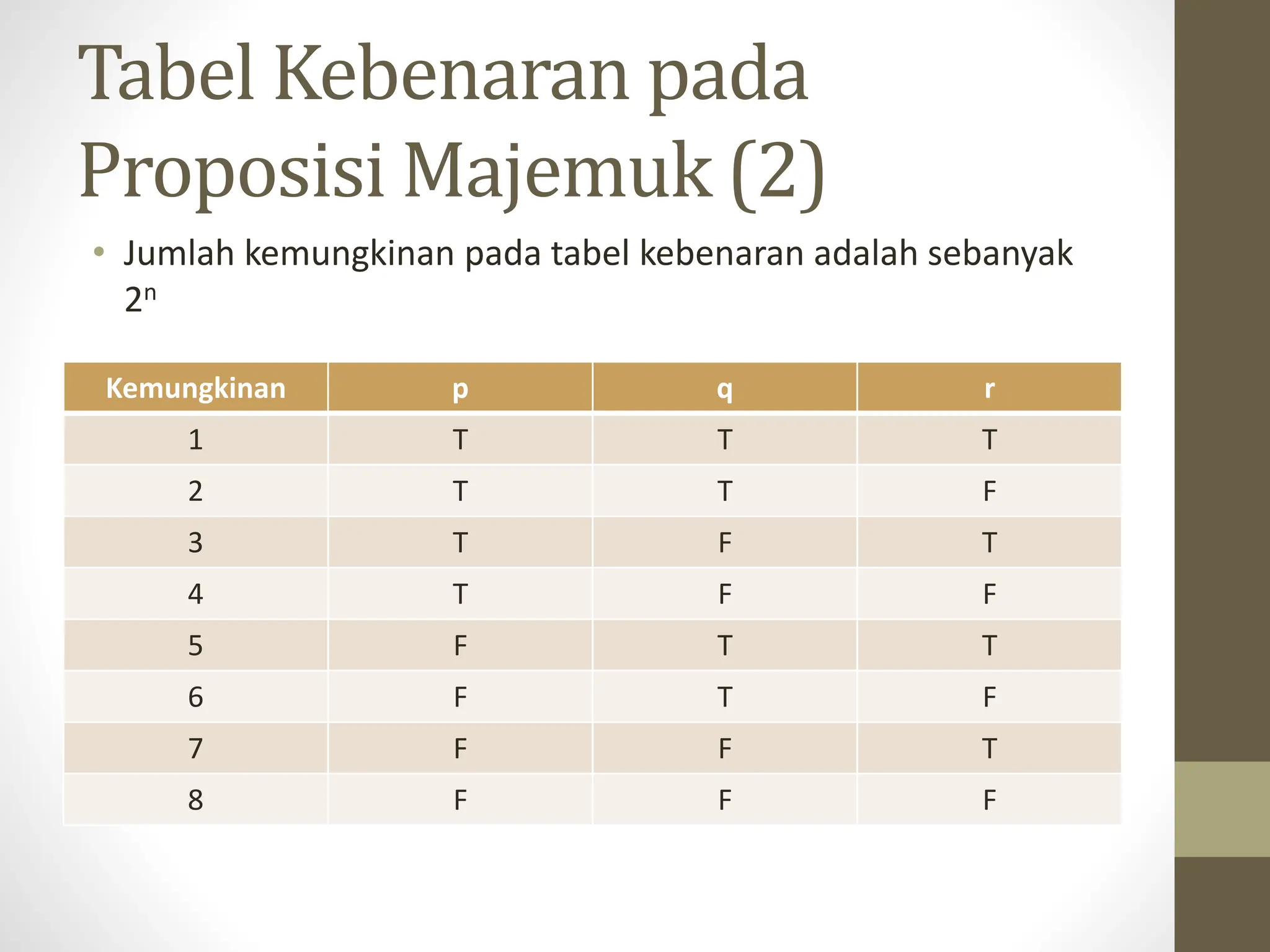
Dokumen ini membahas logika proposisi, termasuk definisi formula dan subformula serta cara membangun tabel kebenaran. Penyajian juga mencakup contoh, latihan soal, dan konsep implikasi serta karakteristik tautologi, kontradiksi, dan kontingensi. Berbagai metode alternatif untuk menentukan nilai kebenaran juga dijelaskan.

1. TABEL KEBENARAN
Minggu -3
Logika Informatika

2. Formula
• Formula (atau kalimat) logika proposisi dibentuk dari:
1. konstanta proposisi: T (benar) dan F (salah)
2. 2 variabel proposisi atom:
p; p1; p2; : : : ;
q; q1; q2; : : : ;
r ; r1; r2; : : :
menggunakan operator –operator logika dengan mengikuti
aturan-aturan berikut:
1. setiap proposisi (atom) merupakan formula logika proposisi,
2. apabila F dan G adalah dua formula logika proposisi, maka :
￢ F, F ∧ G, F ∨ G, F ⊕ G, F → G, F ↔ G, masing-masing juga
merupakan formula logika proposisi.

3. SubFormula
Definisi :
1. Sebuah formula F adalah subformula dari F itu sendiri.
2. Jika F dan G adalah dua formula logika proposisi yang
dipakai untuk membangun formula H yang lebih kompleks,
maka F dan G dikatakan subformula sejati dari H.
3. Subformula bersifat transitif: jika F1 subformula dari F2 dan
F2 subformula dari F3, maka F1 subformula dari F3.
Nilai kebenaran sebuah formula dapat ditentukan dari nilai
kebenaran subformula-subformulanya.

4. SubFormula(2)
• Contoh :
Subformula dari proposisi (p → q) ∨ (q → p) :
• p → q
• q → p
• p
• q
Tentukan subformula dari proposisi berikut :
(￢ p ∧ q) → (p ∧ (q ∨ ￢ r )).

5. Tabel Kebenaran pada
Proposisi Majemuk
• Jika proposisi yang digunakan adalah proposisi atom maka
tabel kebenaran hanya memiliki 2 kemungkinan yaitu T dan F
• Jika proposisi yang digunakan adalah proposisi majemuk maka
jumlah baris kemungkinan pada tabel kebenaran tergantung
pada jumlah variabel yang digunakan.
Kemungkinan p
1 T
2 F
Kemungkinan p q
1 T T
2 T F
3 F T
4 F F

6. Tabel Kebenaran pada
Proposisi Majemuk (2)
• Jumlah kemungkinan pada tabel kebenaran adalah sebanyak
2n
Kemungkinan p q r
1 T T T
2 T T F
3 T F T
4 T F F
5 F T T
6 F T F
7 F F T
8 F F F

7. Cara Alternatif Selain Tabel
Kebenaran
• Jika sudah ditentukan nilai kebenaran dan masing-masing
proposisi atom, bisa menggunakan cara alternatif selain tabel
kebenaran
• Contoh : jika p bernilai T dan q bernilai F maka tentukan nilai
kebenaran dari pernyataan (p∧q) → ￢p
Langkah ( p ∧ q ) → ￢ p
1 T F T
2 F F
3 T

8. Latihan Soal
1. Berapa baris yang digunakan untuk proposisi berikut :
a) p →￢p
b) (p ∨￢r) ∧ (q ∨￢s)
c) q ∨ p ∨￢s ∨￢r ∨￢t ∨ u
d) (p ∧ r ∧ t) ↔(q ∧ t)
2. Buatlah tabel kebenaran untuk proposisi berikut
a) (p ∧ q) → r
b) p ↔ (q ∧ r)

9. Latihan Soal (2)
• Diketahui p bernilai F, q bernilai T dan r bernilai F, tentukan
nilai kebenaran untuk pernyataan berikut
a) p ∨ ￢r
b) q ↔ ￢p
c) p → (￢r ∨ q)
d) (p → q) ∨ r
e) r ↔ (p → ￢q)

10. Implikasi
• Sifat Operator Logika Implikasi :
Implikasi p → q
Konvers q → p
Invers ￢p → ￢q
Kontraposisi ￢q → ￢p

11. Implikasi (2)
• Contoh :
Jika Amir mempunyai mobil maka ia orang kaya
Konvers :
Jika Amir orang kaya maka ia mempunyai mobil
Invers :
Jika Amir tidak mempunyai mobil maka ia bukan orang kaya
Kontraposisi :
Jika Amir bukan orang kaya maka ia tidak mempunyai mobil

12. Implikasi (3)
• Buatlah tabel kebenaran untuk ketiga sifat implikasi tersebut
p q p → q q → p ￢p → ￢q ￢q → ￢p
T T
T F
F T
F F

13. Latihan Soal
• Tentukan Konvers, Invers dan Kontraposisi untuk proposisi
berikut :
a) Jika anda memiliki password yang benar maka anda bisa
login ke facebook
b) Jika saya bosan belajar maka saya akan mendengarkan
musik jazz

14. Tautologi, Kontradiksi,
Kontingensi
• Tautologi : Proposisi selalu bernilai benar
• Kontrakdiksi : Proposisi selalu bernilai salah
• Kontingensi : Proposisi bisa bernilai salah atau bernilai benar
p ￢p p ∨ ￢p
T F T
F T T
p ￢p p ∧ ￢p
T F F
F T F

15. Tautologi – Latihan Soal
• Cek apakah proposisi berikut merupakan tautologi, kontradiksi
atau kontingensi menggunakan tabel kebenaran:
1. (p ∧ q) → [ r ∨ (￢q → ￢r)]
2. (￢p → ￢q) → (q → p)
3. [ p ∧ (p → q) ] → q
4. ￢[ p ∨ (q ∧ r)] ↔ [(p ∨ q) ∧ (p ∨ r)]

16. End