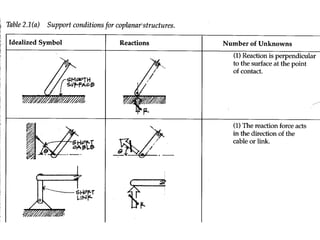
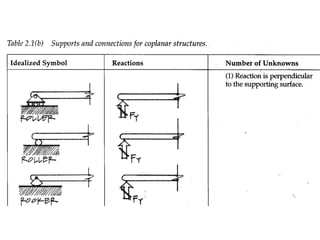
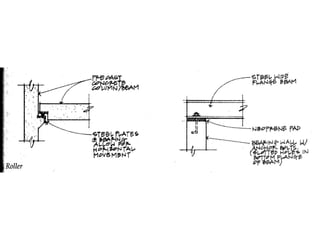
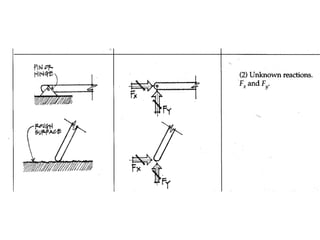
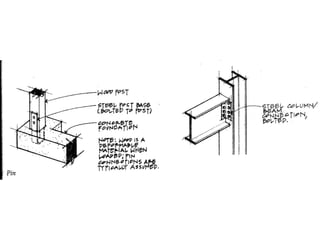
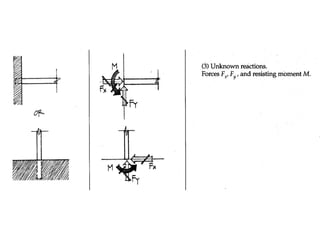
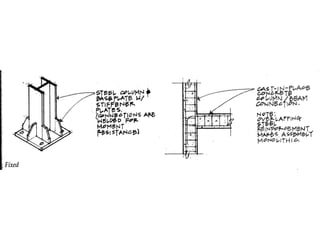
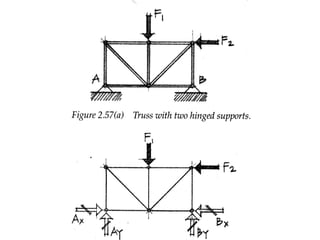
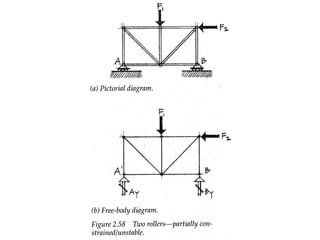
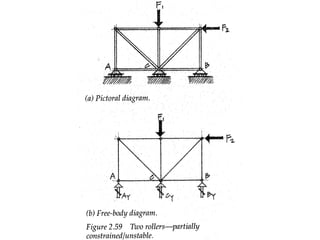
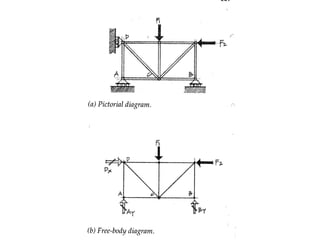
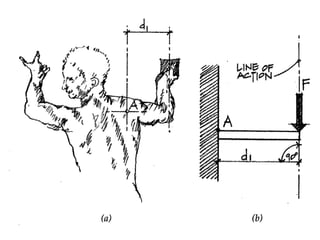
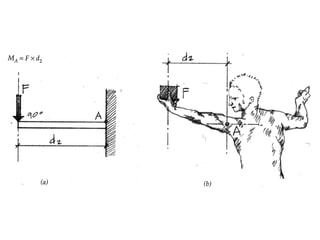
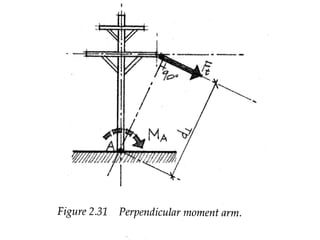
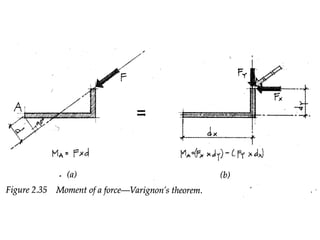
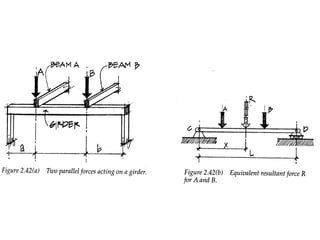
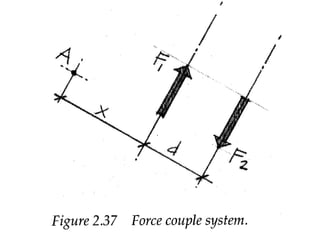
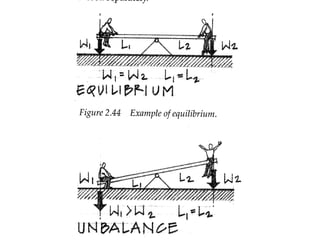
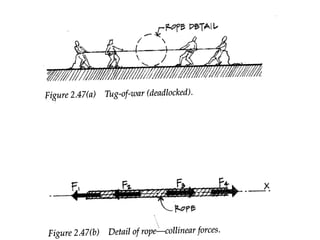
The document defines key concepts related to moments and forces, including: 1) The moment of a force is the tendency of a force to produce rotation about an axis, and is equal to the force magnitude times the perpendicular distance to the axis (moment arm). 2) Varignon's theorem states the algebraic summation of force components about any point equals the moment of the original force. 3) Two parallel forces of equal magnitude but opposite direction form a couple, which causes rotation about an axis perpendicular to its plane. 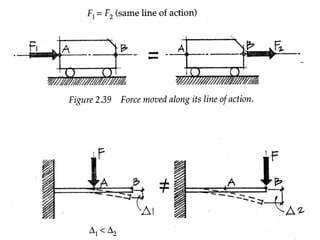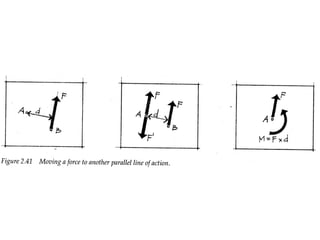4) Forces can be resolved and moved to different points using the principle that the moment of any added couple must equal the original force times the distance of movement.

1. Moment of a Force
• The tendency of a force to produce rotation about
some axis is called the moment of a force.
• The magnitude of this tendency is equal the
magnitude of the force times the perpendicular
distance between the axis and the line of action of
the force (moment arm). M = F * d
• Unit: force x distance =F*L = lb-in, k-in, lb-ft, k-ft
N-m, kN-m (SI unit)
• Sign conven.: clockwise (-), counterclockwise (+)

5. Varignon’s Theorem or the
Principle of Moments
• The algebraic summation of of the
components of a force with respect to any
point is equal to the moment of the original
force.

7. Couples
• Two parallel forces having different lines of
action, equal in magnitude, but opposite in sense
constitute a couple.
• A couple causes rotation about an axis
perpendicular to its plane. M = F * d
– The moment of a couple is independent of the choice of
the axis of moment (moment center)
– A couple cannot be replaced with a single equivalent
resultant force
– A couple may be transferred to any location in its plane
and still have the same effect

9. Resolution of a force into a force
and couple acting at another
point
• Any force F acting on a rigid body may be
moved to any given point A (with a parallel
line of action), provided that a couple M is
added. The moment M of the couple is
equal to F times the perpendicular distance
between the original line of action and the
new location A.

12. Resultant of two parallel forces
• The magnitude of the resultant R of the
parallel forces A and B equals the algebraic
summation of A and B, where R = A + B.
• Location of the resultant R is obtained by
the principle of moments.

14. Equilibrium Equations
• Equilibrium: with zero motion, both the body and
the entire system of external forces and moments
acting on the body are in equilibrium.
• Conditions of equilibrium: the resultant of a force
system must be zero if the force system is to be in
equilibrium:
– The algebraic sum of all forces (or components of
forces) along any axis must be equal to zero (Σ F = 0)
– The algebraic sum of the moments of the forces about
any axis or point must be equal to zero (Σ M = 0)
– In two dimensional case Σ Fx = 0, Σ Fy = 0, Σ M = 0

16. Equilibrium of Force System
• Collinear: if we assume that all the forces
are along the horizontal axis then, Σ Fx = 0
• Concurrent: since the action lines of all
forces intersect at a common point, this
system cannot cause rotation of the body on
which it acts, therefore, only two equations
of equilibrium are sufficient for analyzing
this type of force system, Σ Fx = 0, Σ Fy = 0

19. Equilibrium of Force System
• Parallel: if we assume the forces are parallel
to vertical axis then, Σ Fy = 0, Σ M = 0
• Nonconcurrent coplanar:
Σ Fx = 0, Σ Fy = 0, Σ M = 0

20. The Free Body Diagram (FBD)
• To isolate a body and identify the force system
acting on the body so that unknown forces can be
determined is known as the FBD.
• The external forces acting on the free body may be
direct forces due to contact between the free body
and other bodies external to it or indirect forces,
such as gravitational or magnetic forces, which act
without bodily contact.

29. Statistical Indeterminacy and
Improper Constraints
• When the number of unknown forces exceeds the
number of equations of equilibrium, the rigid body
is said to be statically indeterminate.
• When the support forces are sufficient to resist
translation in both the x and y directions as well as
rotational tendencies about any point, the rigid
body is said to be completely constrained,
otherwise the rigid body is unstable or partially
constrained.