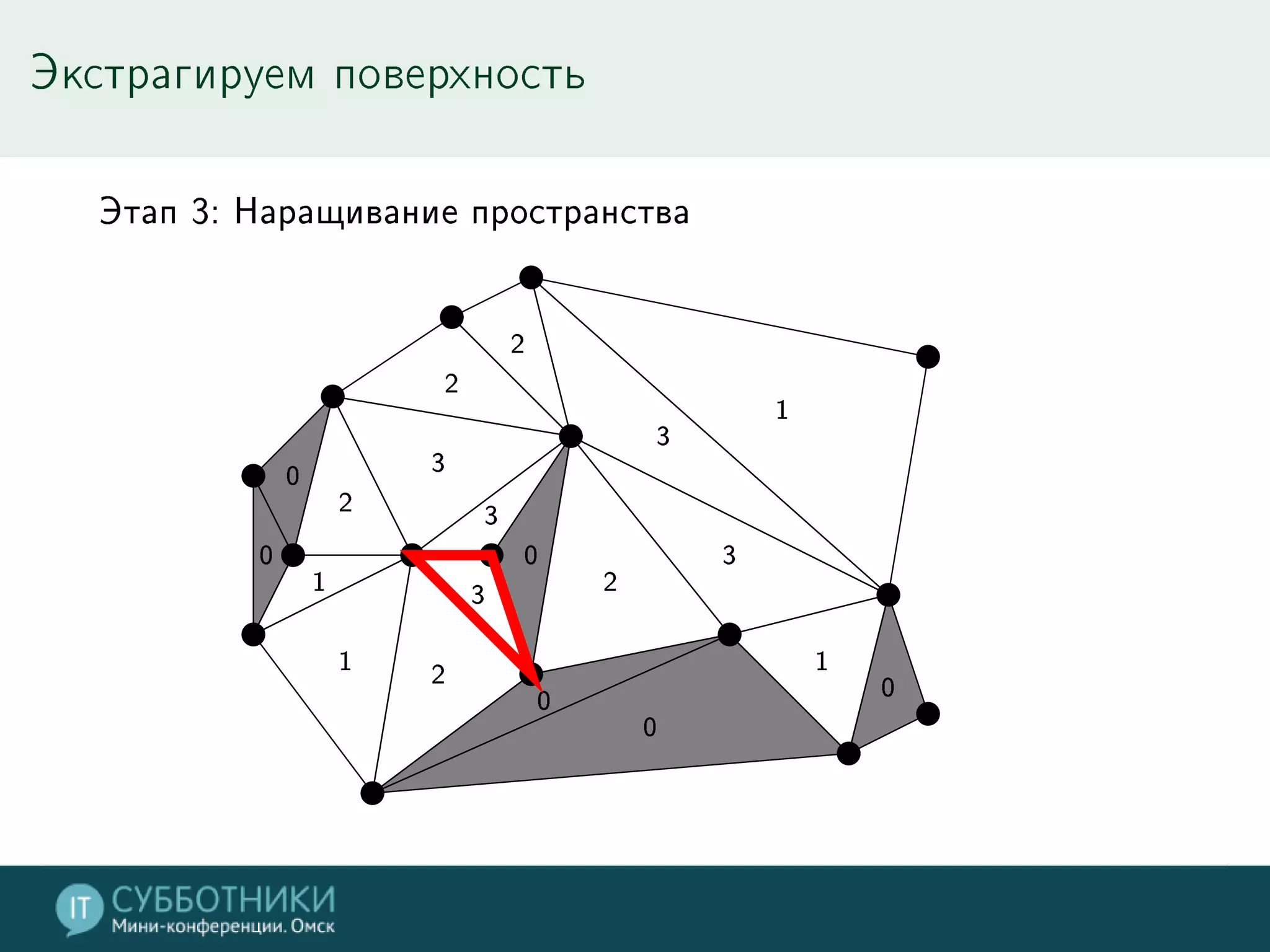
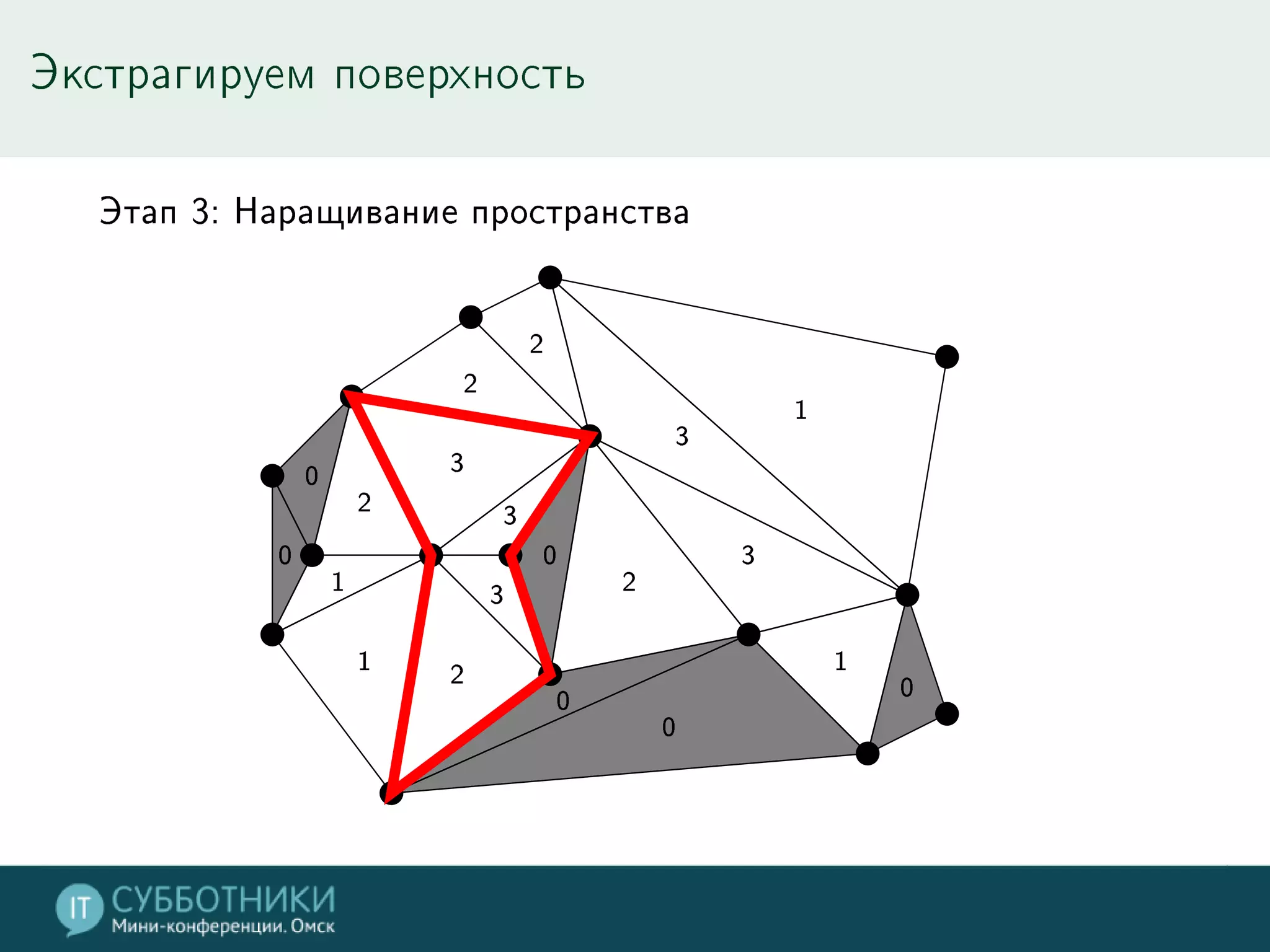
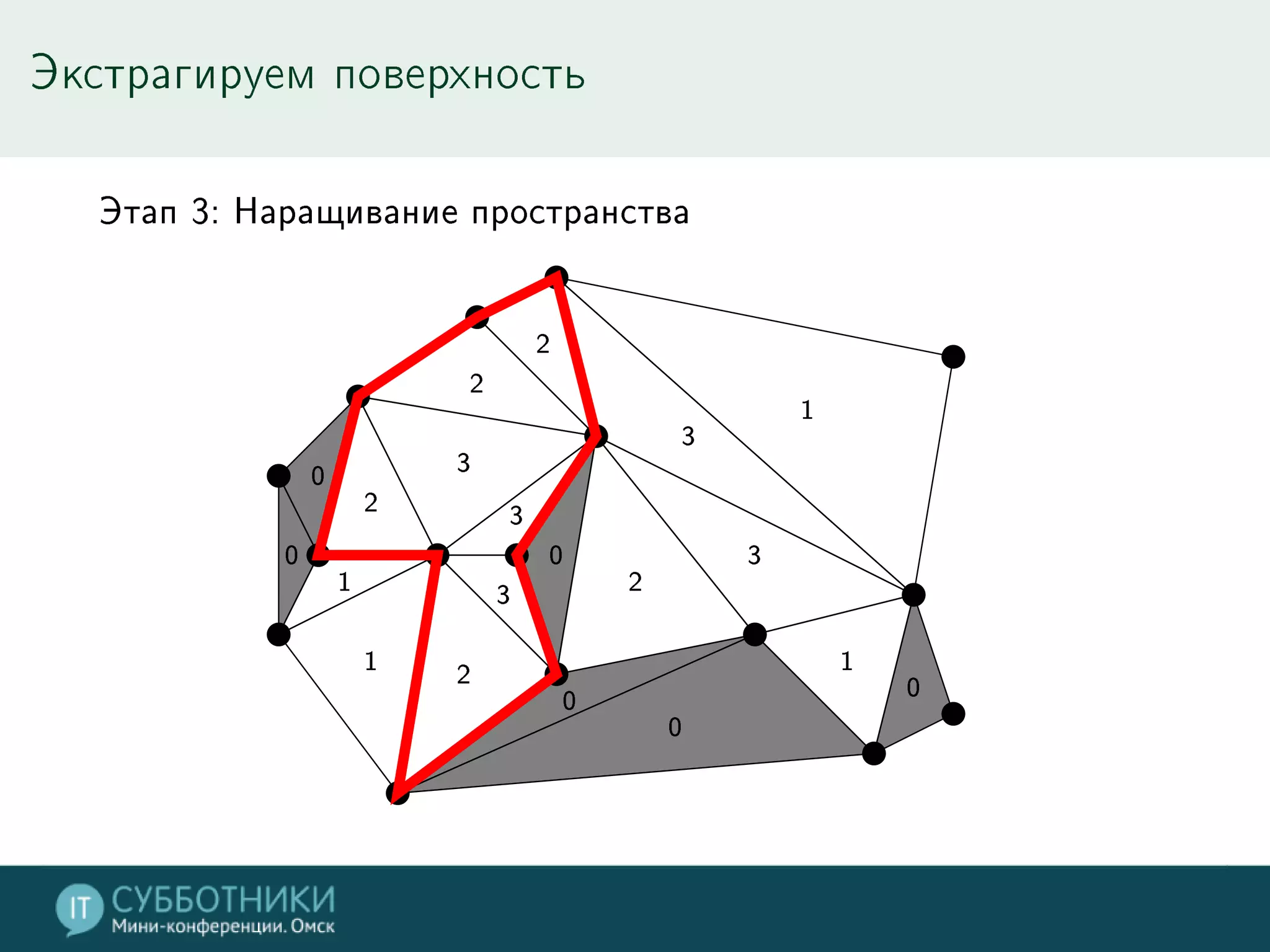
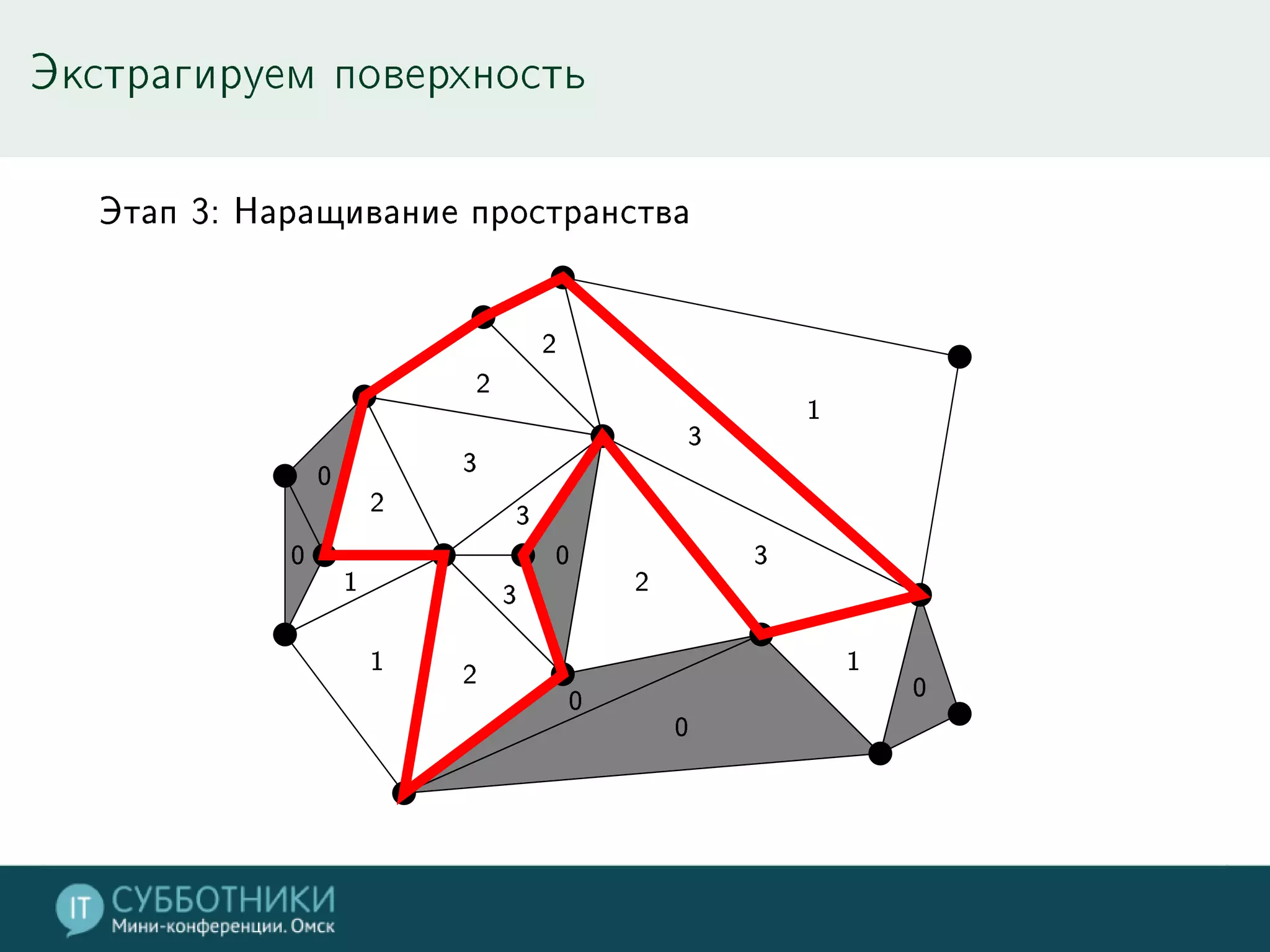
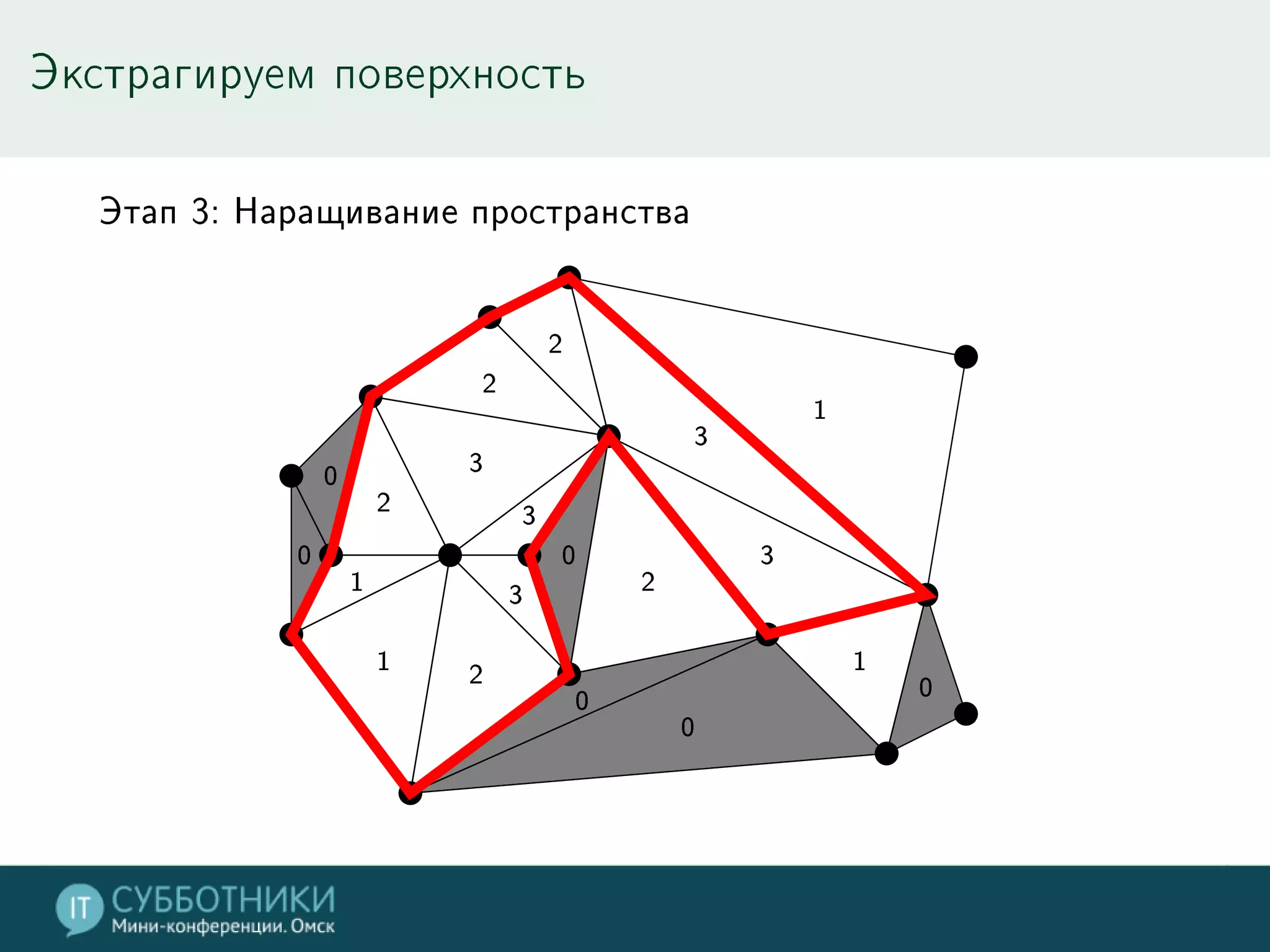
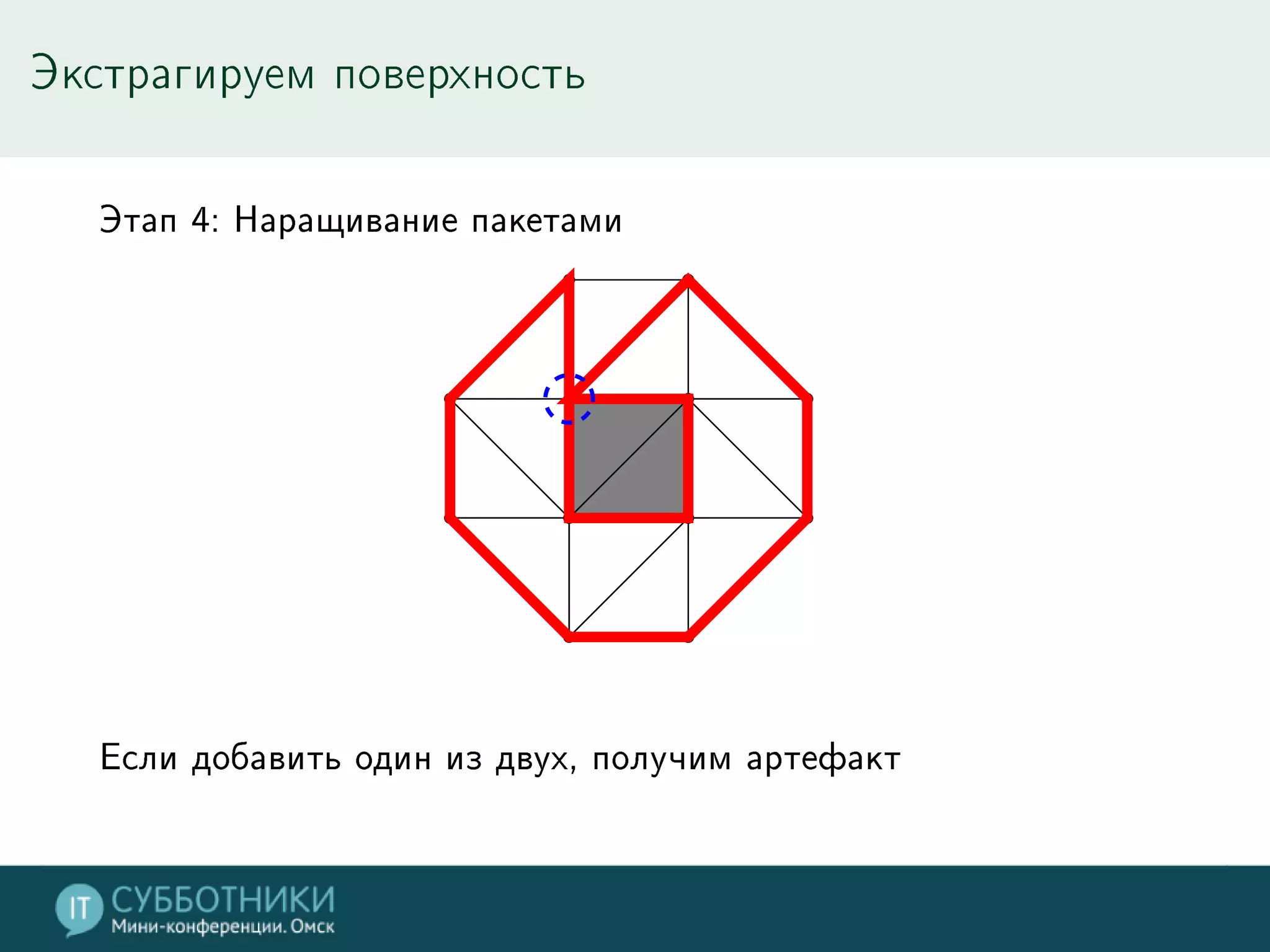
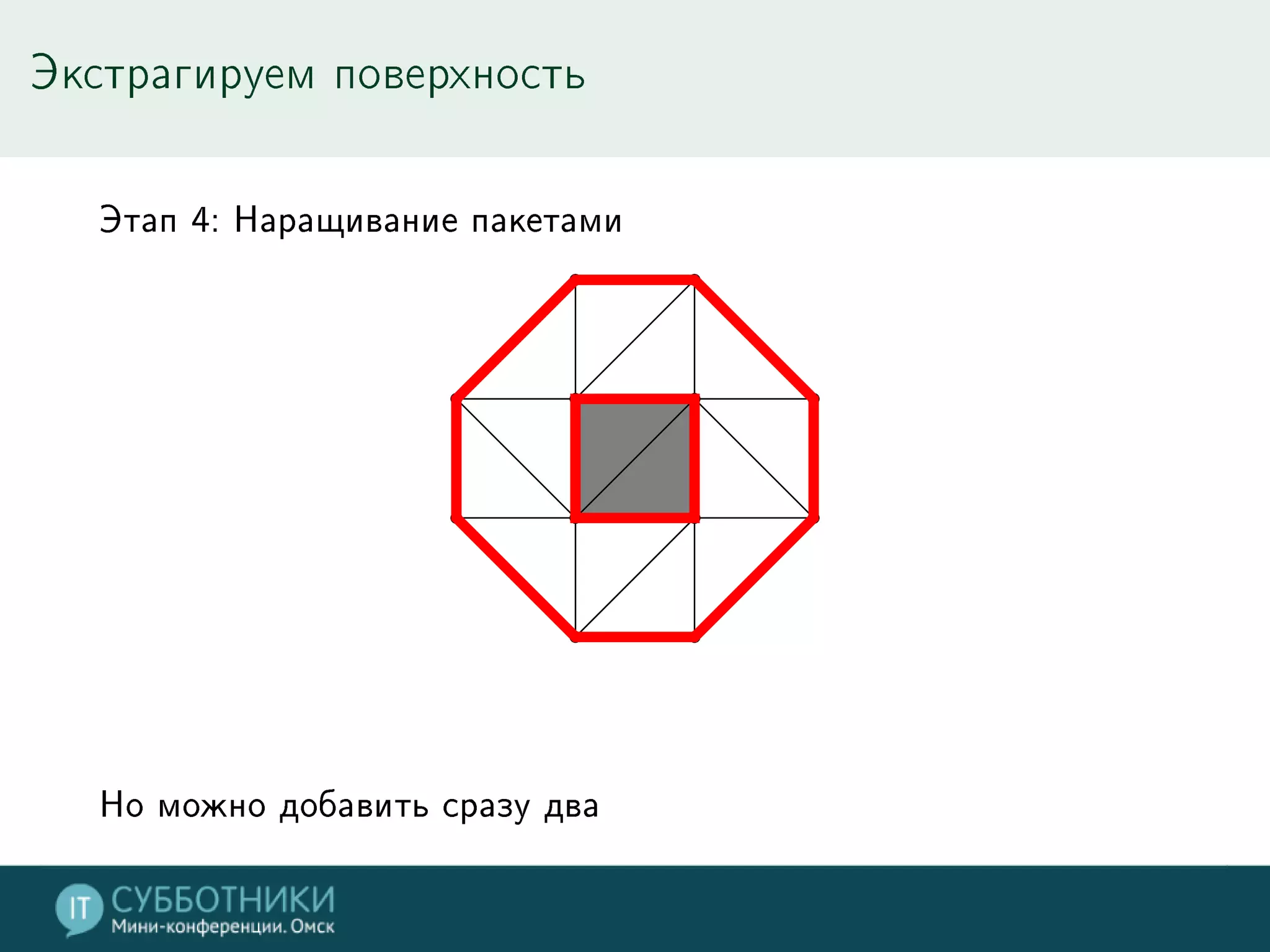
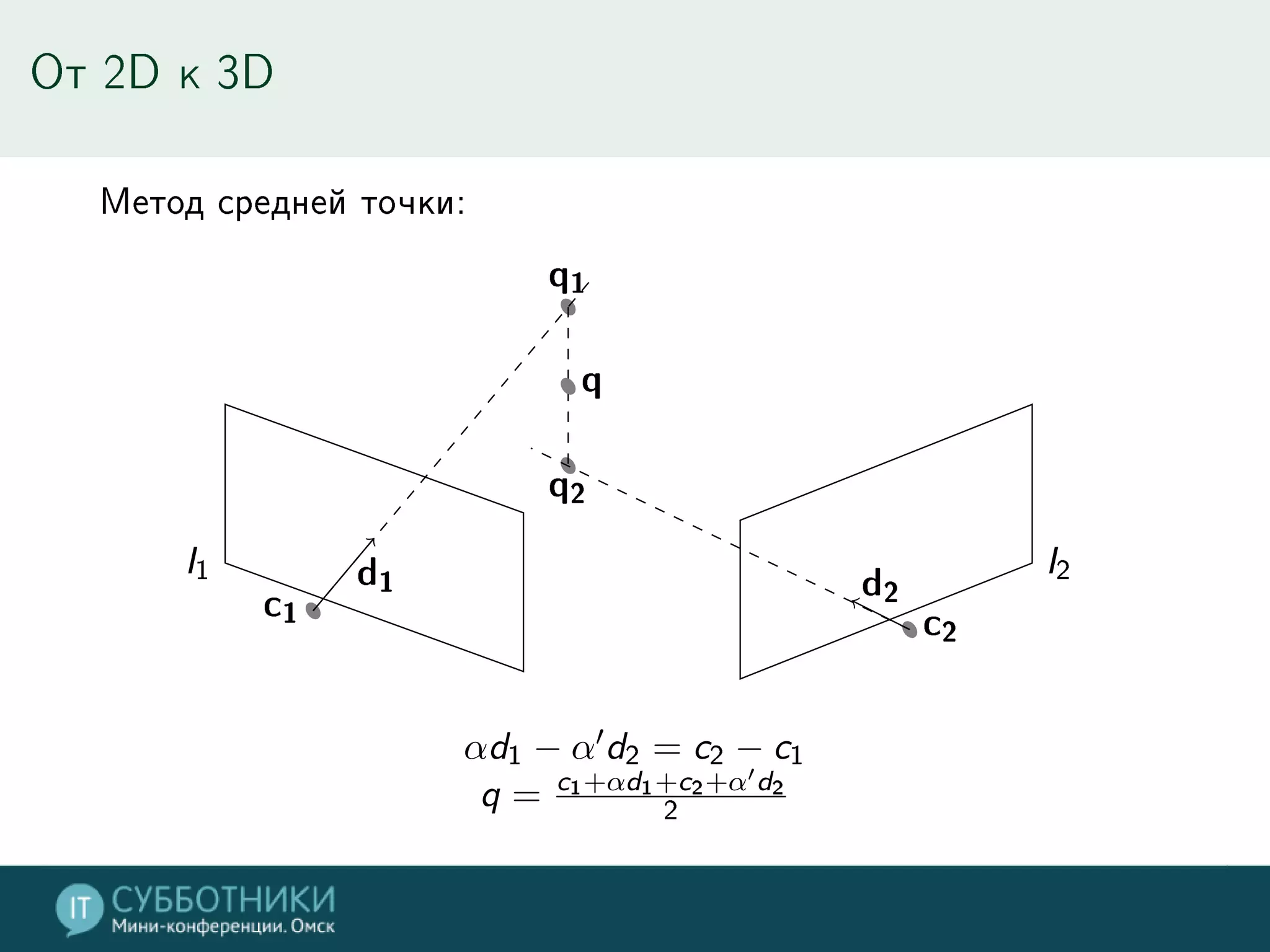
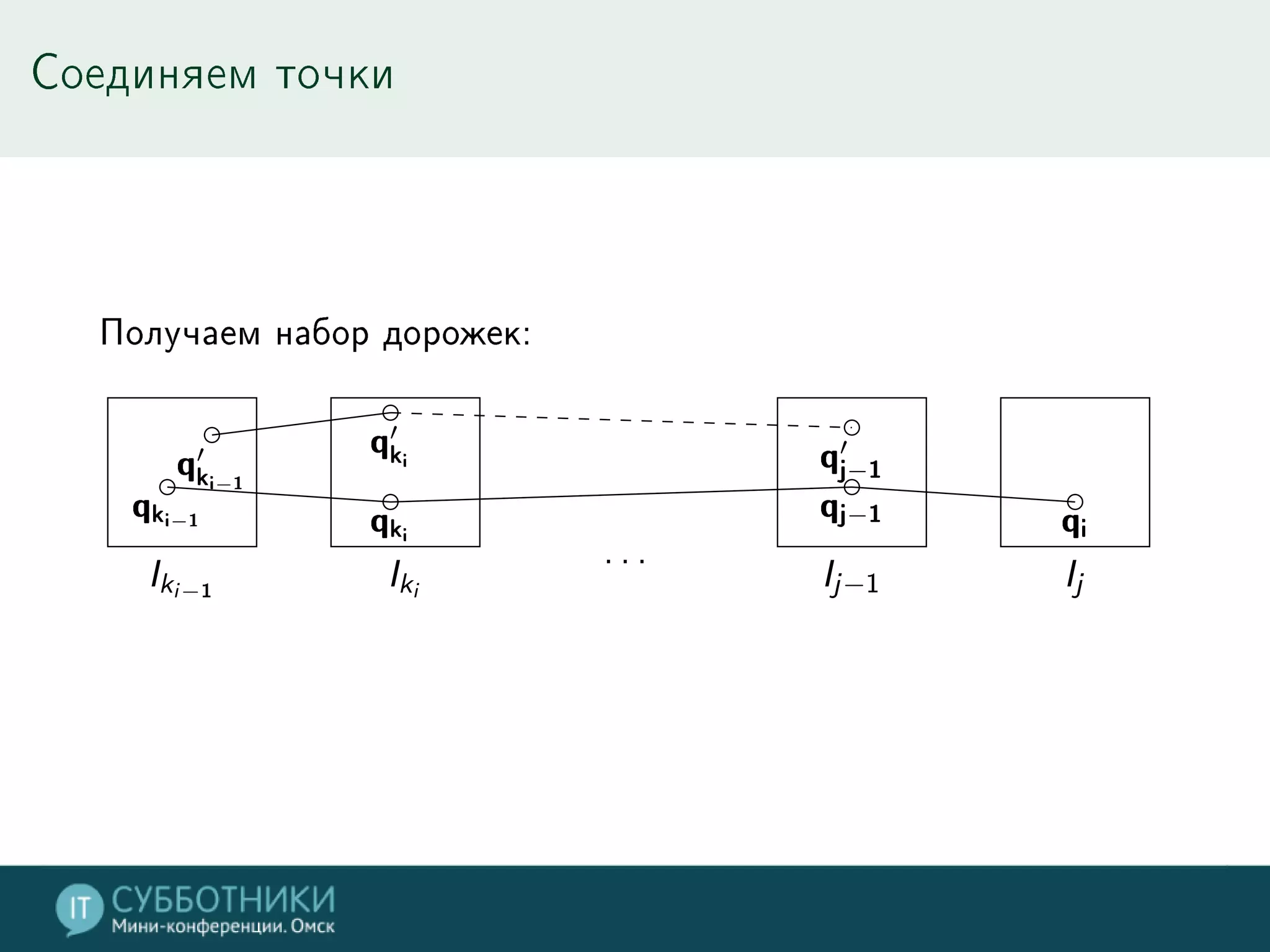
Документ обсуждает методы реконструкции 3D моделей на основе многократных точек обзора, включая математику проекции и алгоритмы для позиционирования камер. Разбираются различные подходы, такие как метод средней точки, алгоритмы SFN и Voxel Coloring, а также их плюсы и минусы. В заключение представлены инструменты для работы с данными и контактная информация автора.

2. Проблематика
Реконструировать 3D модель с помощью нескольких точек
обзора:
+ +

3. Оглавление
1 Введение
2 Изображение и пространство
3 Игры с камерой
4 Пиксели и воксели
5 Неоднородное пространство
6 Заключение

4. Изображение и пространство
2 Изображение и пространство
Моделируем камеру
Позиционируем камеру
От 2D к 3D

5. Моделируем камеру
Стеноп (pinhole camera) в центре мира:
xw
yw
zw
c
c′
q
q′
x
y
c′
y
c′
x
f
q′
y
q′
x

6. Моделируем камеру
Матрица проекции:
⎡
⎣
q′
x
q′
y
1
⎤
⎦ ≡ K
⎡
⎣
qx
qy
qz
⎤
⎦ где K =
⎡
⎣
fx s c′
x
0 fy c′
y
0 0 1
⎤
⎦ (1)
Обратная проекция:
⎡
⎣
d′
x
d′
y
d′
z
⎤
⎦ ≡ K−1
⎡
⎣
q′
x
q′
y
1
⎤
⎦ (2)
⎡
⎣
dx
dy
dz
⎤
⎦ =
1
||(d′
x , d′
y , d′
z)T ||
⎡
⎣
d′
x
d′
y
d′
z
⎤
⎦ (3)

7. Моделируем камеру
Способы убрать оптические искажения линзы:
Работать с выправленными изображениями
Таблицей соответствий
Моделировать их полиномиальной функцией
. . .

8. Позиционируем камеру
Определяем две системы координат:
{xw , yw , zw } - система координат мира
{xc, yc, zc} - система координат камеры
Разница между ними определяется вектором и матрицей:
tw
c - вектор сдвига
Rw
c - матрица поворота
Позиция камеры: {Rw
c , tw
c }

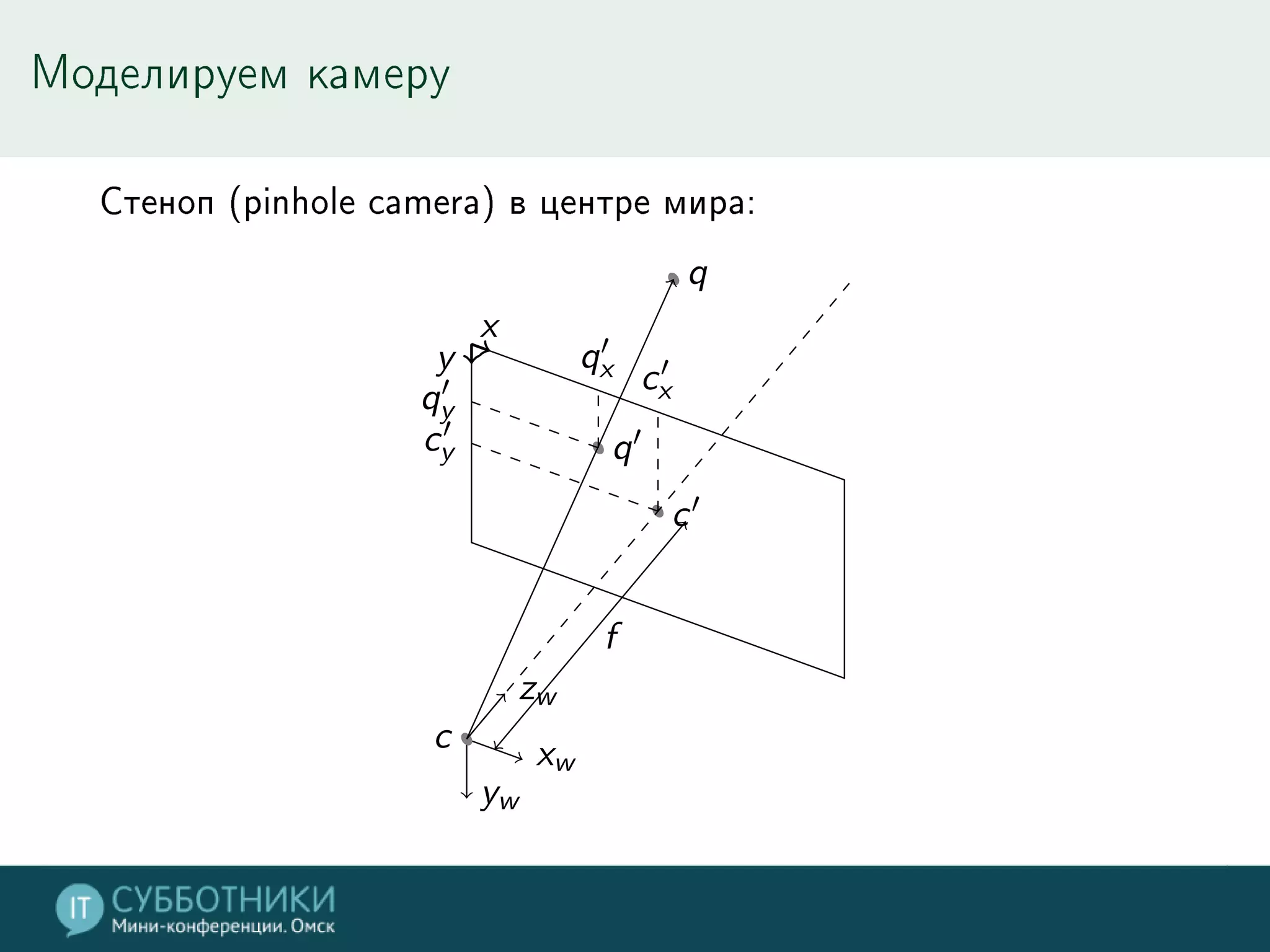
9. Позиционируем камеру
Уравнение проекции:
⎡
⎣
q′
x
q′
y
1
⎤
⎦ ≡ KRwT
c [I3| − tw
c ]
⎡
⎢
⎢
⎣
qx
qy
qz
1
⎤
⎥
⎥
⎦ (4)
Обратная проекция:
⎡
⎣
d′
x
d′
y
d′
z
⎤
⎦ ≡ RwT
c K−1
⎡
⎣
q′
x
q′
y
1
⎤
⎦ (5)

10. От 2D к 3D
Метод средней точки:
c1
I1
c2
I2
q1
q2
q
d1 d2
𝛼d1 − 𝛼′d2 = c2 − c1
q = c1+𝛼d1+c2+𝛼′d2
2

11. Игры с камерой
3 Игры с камерой
Интересные точки
Соединяем точки
Итеративное обновление

12. Алгоритм SfM
Цель: найти относительные позиции камер
фотографировавших каждое изображение.
В этой секции кратко описывается алгоритм:
Etienne Mouragnon, Maxime Lhuillier, Michel Dhome, Fabien
Dekeyser and P. Sayd. Generic and real-time structure from motion
using local bundle adjustment. In Image and Vision Computing
(IVC), vol. 27(8), pp. 1178–1193, july 2009.

13. Интересные точки
Детектор углов Харриса:

14. Интересные точки
Принцип работы:
Нет изменений во
всех направлениях:
плоский регион
Изменения в одном
направлении: грань
Изменения во всех
направлениях: угол

15. Соединяем точки
Можно использовать кросс-корреляцию ZNCC:

16. Соединяем точки
Получаем набор дорожек:
Iki−1 Iki
. . .
Ij−1 Ij
qki−1 qki
qj−1 qi
q′
ki−1
q′
ki q′
j−1

17. Итеративное обновление
Поддерживаем в памяти:
Позиции камер
Облако точек
Для каждого нового изображения (кроме первых трёх):
1 Рассчитываем позицию камеры
2 Рассчитываем координаты новых точек

18. Позиция камеры
1 Мы знаем 3D координаты некоторых
2 Мы знаем их 2D координаты в текущем изображении
3 Трех достаточно что-бы рассчитать позицию камеры
⎡
⎣
q′
x
q′
y
1
⎤
⎦ ≡ KRwT
c [I3| − tw
c ]
⎡
⎢
⎢
⎣
qx
qy
qz
1
⎤
⎥
⎥
⎦ (6)

19. Вводим понятие ошибки
Разница между теоретическим и реальным результатом:
c
q′
q
d′
q dq
𝛼q

20. Добавим надёжность
Используем RANSAC:
Выбираем 3 случайных точки
Рассчитываем позицию камеры
Рассчитываем ошибку для всех 3D точек
Их сумма в квадрате очки этого результата
Повторяем N раз
Оставляем результат с наименьшим количеством очков

21. Считаем точки и оптимизируем
Считаем координаты 3D точек:
Рассчитываем 3D координаты точек видимых как
минимум в 3 кадрах
Используем третий кадр для проверки
Оптимизируем результат при помощи алгоритма
Levenberg-Maquard:
Улучшаем позицию 3 последних камер
Улучшаем точки видимые в 10 последних кадрах

22. Инициализация процесса
Мы работаем с 3 первыми кадрами
Если мы знаем соответствия между 5 точками в двух
кадрах:
Мы можем рассчитать позиции камер
И 3D координаты этих точек
Мы рассчитываем координаты первой и третьей камеры
Потом мы рассчитываем координаты второй
Используем RANSAC для надёжности

23. Пиксели и воксели
4 Пиксели и воксели
Метод и его ограничения
Разделяем и сортируем
Красим воксели
Результаты
Плюсы и минусы

24. Voxel coloring
Рассмотрим метод описанный в
Steven M. Seitz, Charles R. Dyer. Photorealistic scene
reconstruction by voxel coloring. In International Journal of
Computer Vision (IJCV), vol. 35(2), pp. 151–173, november 1999

25. Ограничения
Объем занимаемый камерами должен быть вне
реконструироемой сцены.

26. Разделяем пространство
Равномерно делим пространство на воксели:

27. Сортируем воксели
Сортируем воксели по дальности от камеры:
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
6
6
6
6
6
6
6
6
6
6
7
7
7
7
7
7
7
7
7
7
8
8
8
8
8
8
8
8
8
8
9
9
9
9
9
9
9
9
9
9
10
10
10
10
10
10
10
10
10
10

28. Красим воксели
Обрабатываем слой за слоем:
Для каждого вокселя:
Для каждой камеры Ci :
Проецируем воксель в камеру
Проверяем что луч от вокселя к камере не пересекает
заполненных вокселей
Запоминаем цвет ci соответствующего пикселя
Считаем корреляцию между цветами c1,. . . ,cn:
Если корреляция заданного значения:
Помечаем воксель как заполненный
Цвет вокселя, среднее между c1,. . . ,cn
Если меньше: воксель отмечается как пустой

29. Заполненный воксель
Пример заполненного вокселя:

30. Пустой воксель
Пример пустого вокселя:

31. Результат: динозавр

32. Результат: роза

33. Плюсы и минусы
Плюсы:
Простота реализации
Хорошие результаты
Минусы:
Объект должен быть цветастым
Большое количество вычислений
Огромное потребление памяти с ростом размера модели

34. Неоднородное пространство
5 Неоднородное пространство
Описание метода
Делим пространство
Экстрагируем поверхность
Результаты
Плюсы и минусы

35. Space carving
Рассмотрим метод описанный в
Maxime Lhuillier, Shuda Yu. Manifold surface reconstruction of an
environment from sparse Structure-from-Motion data. In Computer
Vision and Image Understanding (CVIU), vol. 117(11), pp.
1628–1644, november 2013.
На вход он принимает позиции камер и облако точек и связи
между ними

36. Делим пространство
Этап 1: Рассчитываем триангуляцию Делоне

37. Делим пространство
Этап 2: Сортируем тетраэдры на пустые и полные
00
2
0
2
0
2
3
2
0
2
0
0
0
0
0
0
c1
c2

38. Экстрагируем поверхность
Если использовать границу между свободным и заполненным
пространством из предыдущего этапа, то поверхность будет
некорректна.
Корректно Артефакт

39. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

40. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

41. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

42. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

43. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

44. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

45. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

46. Экстрагируем поверхность
Этап 3: Наращивание пространства
0
1
1
2
0
2
2
0
3
2
2
3
3
1
0
1
0
3
3
0

47. Экстрагируем поверхность
Этап 4: Наращивание пакетами
Мы хотим добавить два оставшихся тетраэдра

48. Экстрагируем поверхность
Этап 4: Наращивание пакетами
Если добавить один из двух, получим артефакт

49. Экстрагируем поверхность
Этап 4: Наращивание пакетами
Но можно добавить сразу два

50. Экстрагируем поверхность
Резюме алгоритма:
1 Добавляем тетраэдры по одному, пока возможно
2 Для каждой вершины поверхности:
1 Пытаемся добавить тетраэдры содержащие вершину
одновременно
2 Если получилось, останавливаем цикл
3 Если пустое пространство увеличилось, goto 1

51. Результат: Церковь

52. Результат: Город

53. Плюсы и минусы
Плюсы:
Быстрота вычислений
Возможность работать с большими пространствами
Минусы:
Визуальный результат среднего качества

54. Заключение
Надеюсь что реконструкция поверхностей больше не кажется
вам черной магией.
Полезные инструменты:
OpenCV - http://opencv.org
Ceres - http://ceres-solver.org
CGAL - http://www.cgal.org
Для связи со мной: vadim_litvinov (Гав-гав!) fastmail.com