2004/06/25 授業「情報の科学」

1. 情報の表現
コンピュータでの数値の表現

2. 2進数とは?
• 0と1で表す(0,1,10,11,100,101,110,111,･･･)
• 電子コンポーネントの2つの状態を表す
– 1はON
– 0はOFF
• 1ビット(1b)は2進数の1桁を意味する
• 2進数8桁(8ビット)のことを1バイト(1B)という
• 情報の単位
– K(キロ),M(メガ),G(ギガ) ,T(テラ),P(ペタ)
1024倍 1024倍 1024倍 1024倍

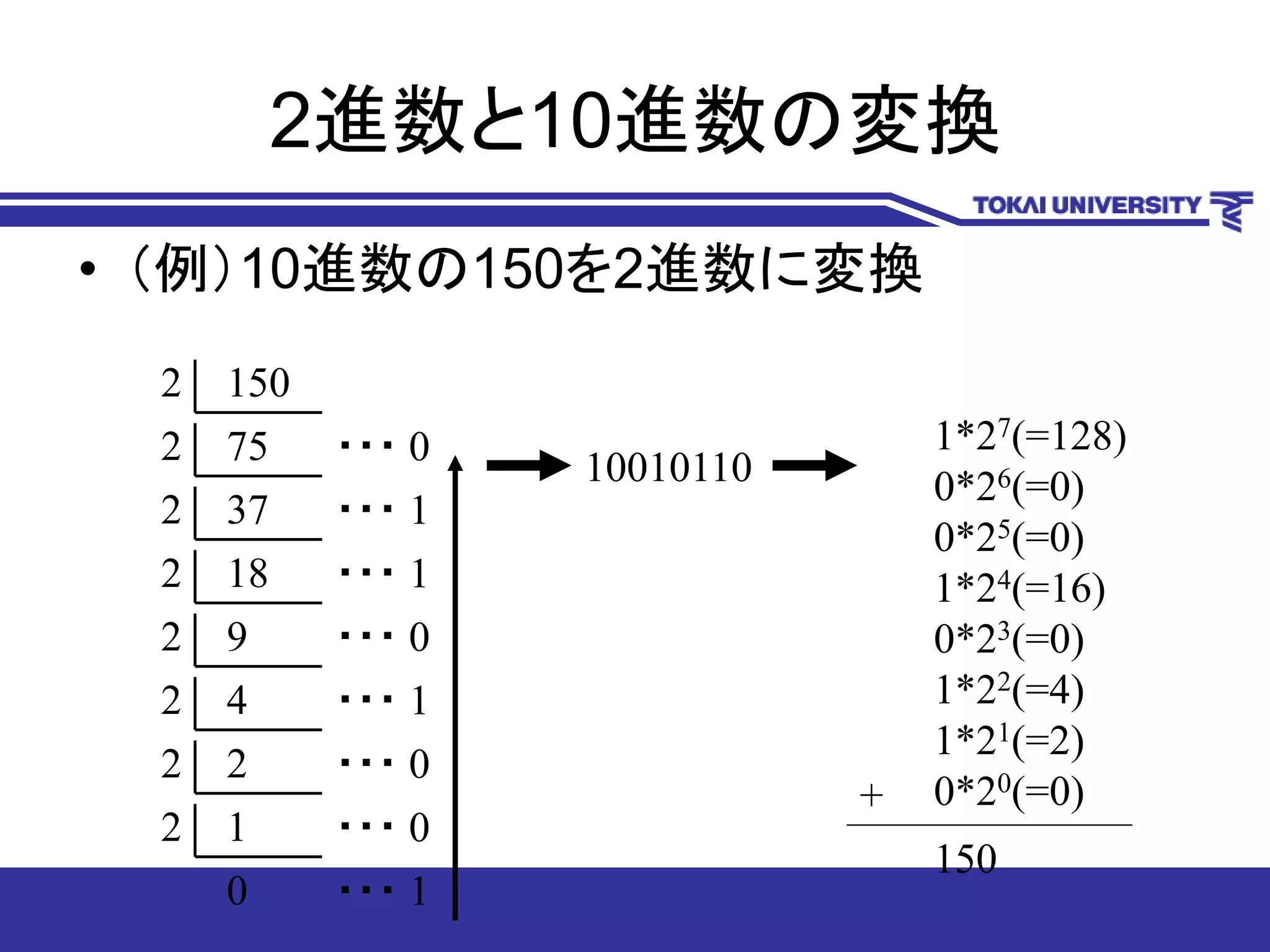
3. 2進数と10進数と16進数
• 10進数（基数10）
– 記号：0,1,2,3,4,5,6,7,8,9（10コ）
– 例：126=1*102+2*101+6*100 =100+20+6
• 2進数（基数2）
– 記号:0,1（2コ）
– 例：110=1*22+1*21+0*20=4+2+0=6
• 16進数（基数16）
– 記号:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
– 例：2F=2*161+F(15)*160=32+15=47

4. 2進数と10進数の変換
• （例）10進数の150を2進数に変換
1502
2 75 ・・・ 0
2 37 ・・・ 1
2 18 ・・・ 1
2 9 ・・・ 0
2 4 ・・・ 1
2 2 ・・・ 0
2 1 ・・・ 0
0 ・・・ 1
10010110
+
150
1*27(=128)
0*26(=0)
0*25(=0)
1*24(=16)
0*23(=0)
1*22(=4)
1*21(=2)
0*20(=0)

5. 2進数と16進数の変換
• （例）2進数の10010110を16進数に変換
• 2進数4桁は16進数1桁で表現できる
– ２4=16 ⇔ 161=16
1001 0110
10進数で9 10進数で6
96( )16

6. 整数の表現
• 32ビット(4バイト)の符号付き整数(正の数)
• 10進数150の場合
– 符号部 ⇒ 0
– 数値部 ⇒ 0000000000000000000000010010110
– したがって⇒ 00000000000000000000000010010110
– 16進数では⇒ 0 0 0 0 0 0 9 6
符号部
(1bit)
0なら正
1なら負
数値部(31bit) 20212223・・・・・230 ・・・・・

7. 整数の表現
• 32ビット(4バイト)の符号付き整数(負の数)
• 負の数は2の補数で表す
• 基数rの正数Nに対するrの補数Crは、
次式で与えられる。
– Cr = rn – N (nはNの整数部の桁数)
• (例1)150の10の補数⇒103 - 150 = 850
• (例2)0.75の10の補数⇒100 – 0.77 = 0.23

8. 整数の表現
• 32ビット(4バイト)の符号付き整数(負の数)
• 負の数は2の補数で表す
• 2進数の2の補数の求め方
– 「0と1を反転させて、1を加える。」
• (例1)(1101)2の2の補数⇒(0010)2 +(0001)2 =(0011)2
• (例2)(10010110)2の2の補数
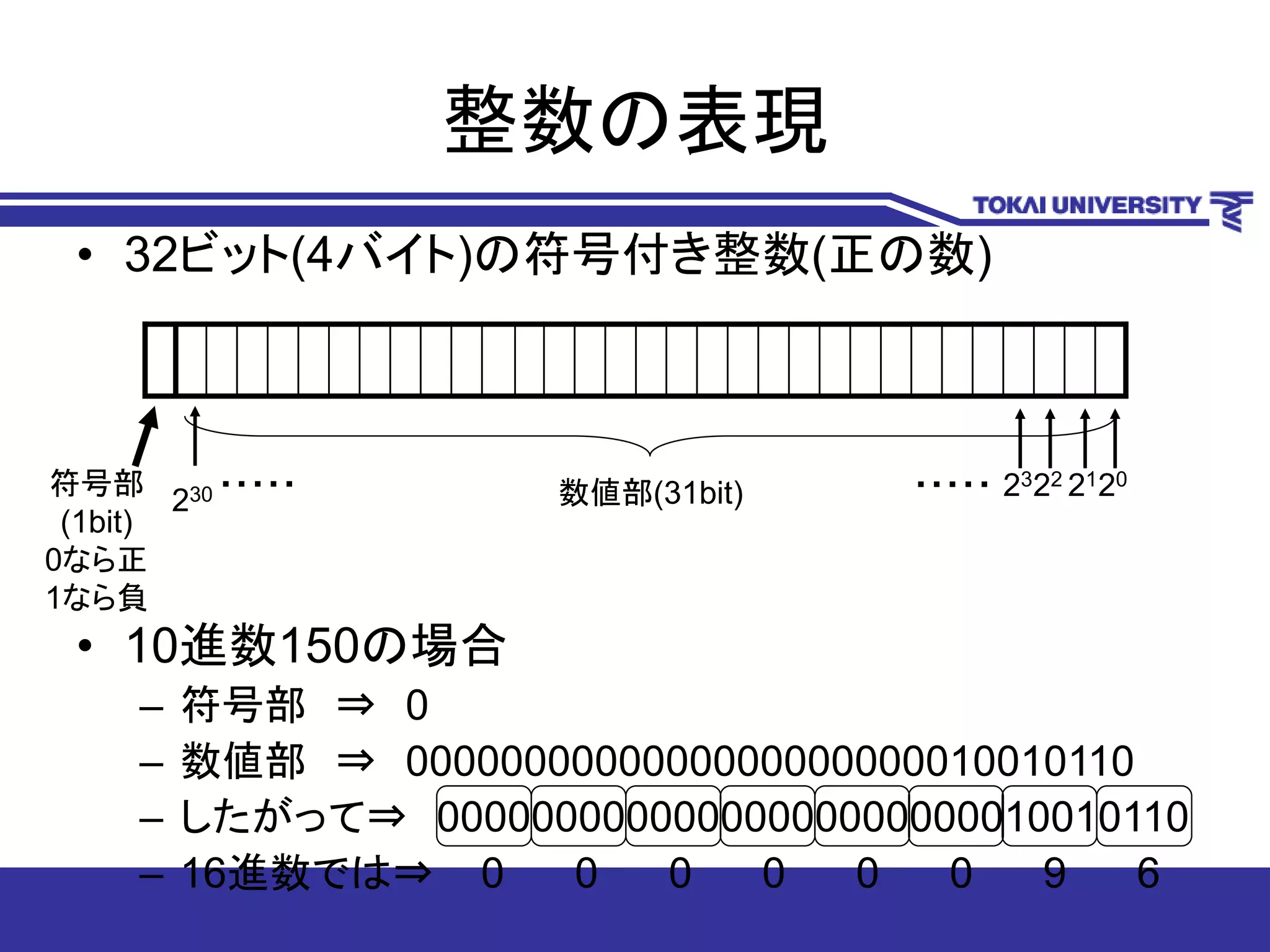
⇒(01101010)2 + (00000001)2 =(01101011)2

9. 整数の表現
• 32ビット(4バイト)の符号付き整数(負の数)
• 負の数は2の補数で表す
• 10進数-150の場合
– 150を2進数31桁で表すと
0000000000000000000000010010110
– 0と1を反転させて
1111111111111111111111101101010
– 1を加える
1111111111111111111111101101011
– 符号部は1であるから、これを追加して。
1 1111111111111111111111101101011
– 16進数では FFFFFF6A

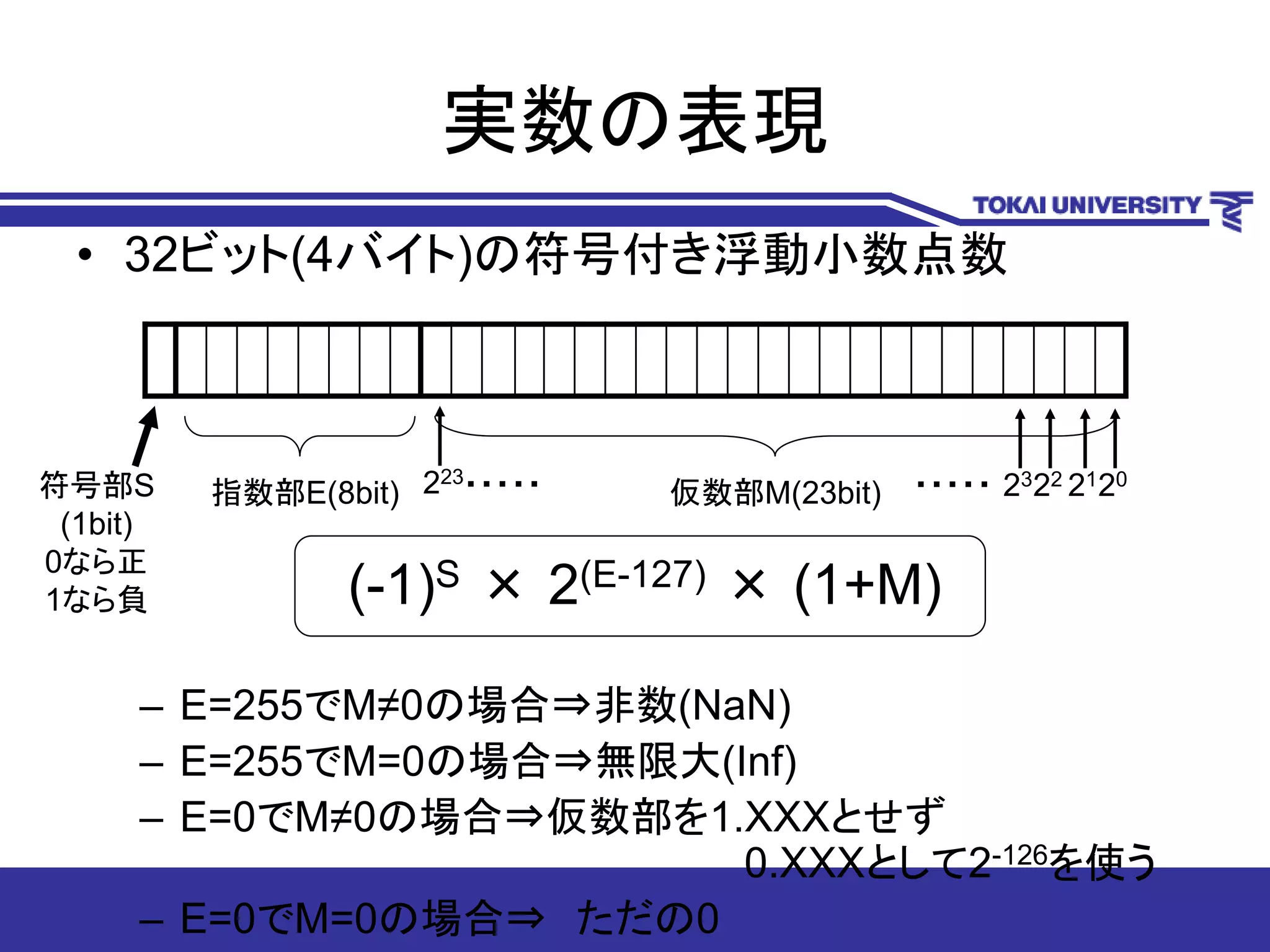
10. 実数の表現
• 指数形式
– a × rn
– (例1)
3.14 ⇒ 3.14×1 ⇒ 3.14×100 ⇒ 3.14e0
– (例2)
3776 ⇒ 3.776×1000 ⇒ 3.776×103 ⇒ 3.776e3
3.776 e 3
指数部仮数部

11. 実数の表現
• 32ビット(4バイト)の符号付き浮動小数点数
– E=255でM≠0の場合⇒非数(NaN)
– E=255でM=0の場合⇒無限大(Inf)
– E=0でM≠0の場合⇒仮数部を1.XXXとせず
0.XXXとして2-126を使う
– E=0でM=0の場合⇒ ただの0
符号部S
(1bit)
0なら正
1なら負
仮数部M(23bit) 20212223・・・・・223
・・・・・指数部E(8bit)
(-1)S × 2(E-127) × (1+M)

12. 実数の表現
• 32ビット(4バイト)の符号付き浮動小数点数
• 10進数11.625の場合
– まず、2進数で表す。
– 11.625 ⇒ (1011.101)2 ⇒ (1.011101)2×23
– 符号部 ⇒ S=0
– 指数部 ⇒ 3=E-127 ⇒ E=130 ⇒ 10000010
– 仮数部 ⇒ 01110100000000000000000
– したがって
0 10000010 01110100000000000000000
– 16進数では 4 1 3 A 0 0 0 0
– 負の数の場合は、符号部が1になるだけ
(小数点以下のみ取る)

13. コンピュータ内部での保存形式
• 150を16進数で表すと ⇒ 00 00 00 96
• 11.625を16進数で表すと ⇒ 41 3A 00 00
• bosei(CPUがSPARCプロセッサ)の場合
– 上の表記のまま
• パソコン(正確にはIntelのCPU)場合
– 1バイトずつに区切って、左右が入れ替わる。
– 150を16進数で表すと ⇒ 96 00 00 00
– 11.625を16進数で表すと ⇒ 00 00 3A 41

14. 文字の表現
• 変換表が必要
• アルファベットを表現
– 26個の情報 ⇒ 24=32 ⇒ 4ビットあればよい
• アルファベット大文字・小文字＋数字＋記号
– 27=128 ⇒ 7ビットあればよい
• ASCIIコード
– (例)A ⇒ (41)16 b ⇒ (62)16 # ⇒ (23)16

15. 文字の表現
• ASCIIコード
上位３ビット
0 1 2 3 4 5 6 7
下 0 <NUL> <DLE> <SP> 0 @ P ` p
位 1 <SOH> <DC1> ! 1 A Q a q
4 2 <STX> <DC2> " 2 B R b r
ビ 3 <ETX> <DC3> # 3 C S c s
ッ 4 <EOT> <DC4> $ 4 D T d t
ト 5 <ENQ> <NAK> % 5 E U e u
6 <ACK> <SYN> & 6 F V f v
7 <BEL> <ETB> ' 7 G W g w
8 <BS> <CAN> ( 8 H X h x
9 <HT> <EM> ) 9 I Y i y
A <NL> <SUB> * : J Z j z
B <VT> <ESC> + ; K [ k {
C <NP> <FS> , < L ¥ l |
D <CR> <GS> - = M ] m }
E <SO> <RS> . > N ^ n ~
F <SI> <US> / ? O _ o <DEL>

16. 文字の表現
• 日本語の表現
– ひらがな(50音+α)
– カタカナ(50音+α)
– 漢字(数万種類)
• 2バイト(16bit=65535)で表現
– JISコード
– シフトJISコード
– EUCコード

17. 文字の表現
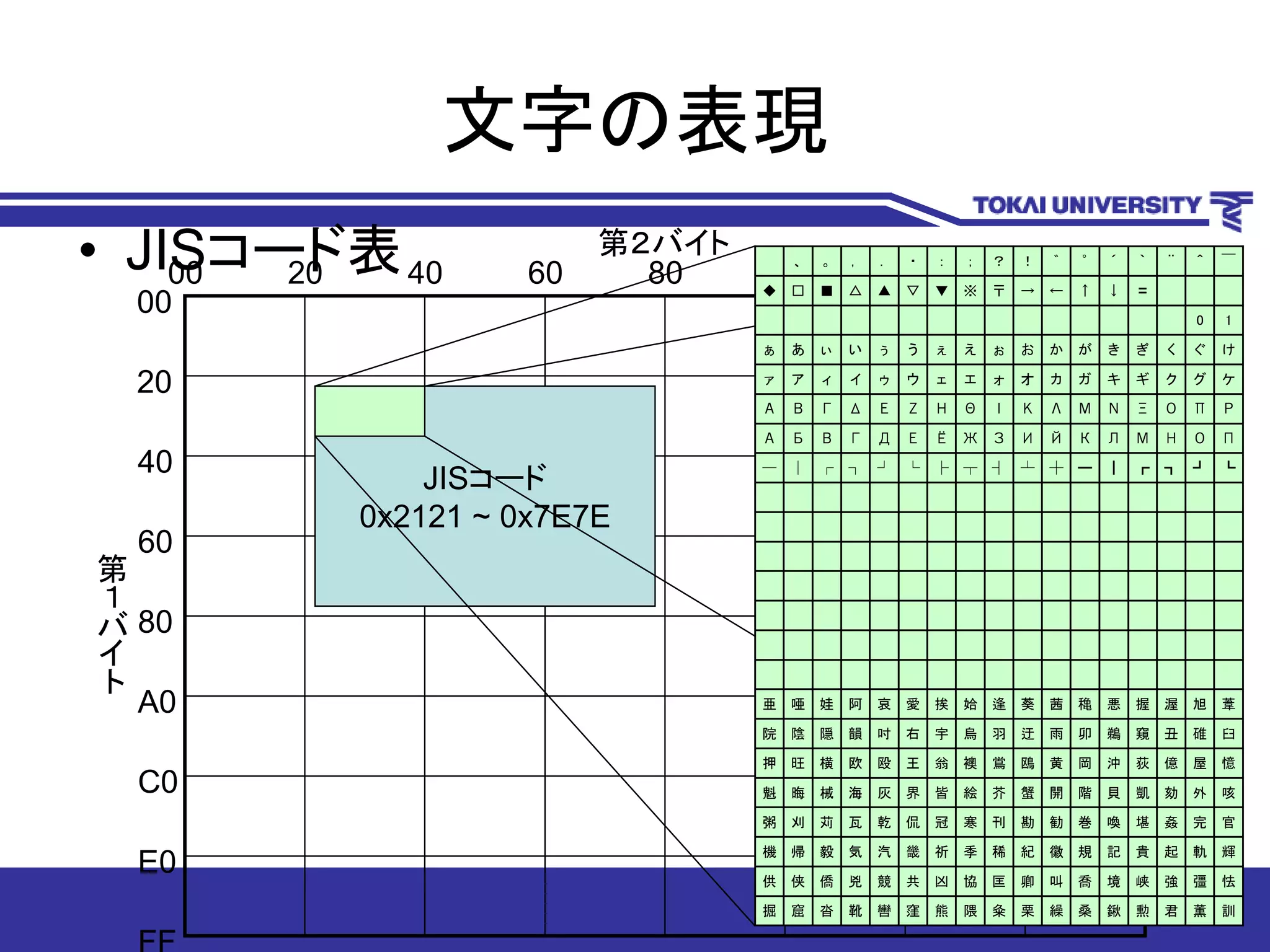
• JISコード表
20
00
40
60
80
A0
C0
E0
2000 40 60 80 A0 C0 E0 FF
JISコード
0x2121 ~ 0x7E7E
第
１
バ
イ
ト
第２バイト
訓薫君勲鍬桑繰栗粂隈熊窪轡靴沓窟掘
怯彊強峡境喬叫卿匡協凶共競兇僑侠供
輝軌起貴記規徽紀稀季祈畿汽気毅帰機
官完姦堪喚巻勧勘刊寒冠侃乾瓦苅刈粥
咳外劾凱貝階開蟹芥絵皆界灰海械晦魁
憶屋億荻沖岡黄鴎鴬襖翁王殴欧横旺押
臼碓丑窺鵜卯雨迂羽烏宇右吋韻隠陰院
葦旭渥握悪穐茜葵逢姶挨愛哀阿娃唖亜
┗┛┓┏┃━┼┴┤┬├└┘┐┌│─
ПОНМЛКЙИЗЖЁЕДГВБА
ΡΠΟΞΝΜΛΚΙΘΗΖΕΔΓΒΑ
ケグクギキガカオォエェウゥイィアァ
けぐくぎきがかおぉえぇうぅいぃあぁ
10
〓↓↑←→〒※▼▽▲△■□◆
￣＾¨｀´゜゛！？；：・．，。、

18. 文字の表現
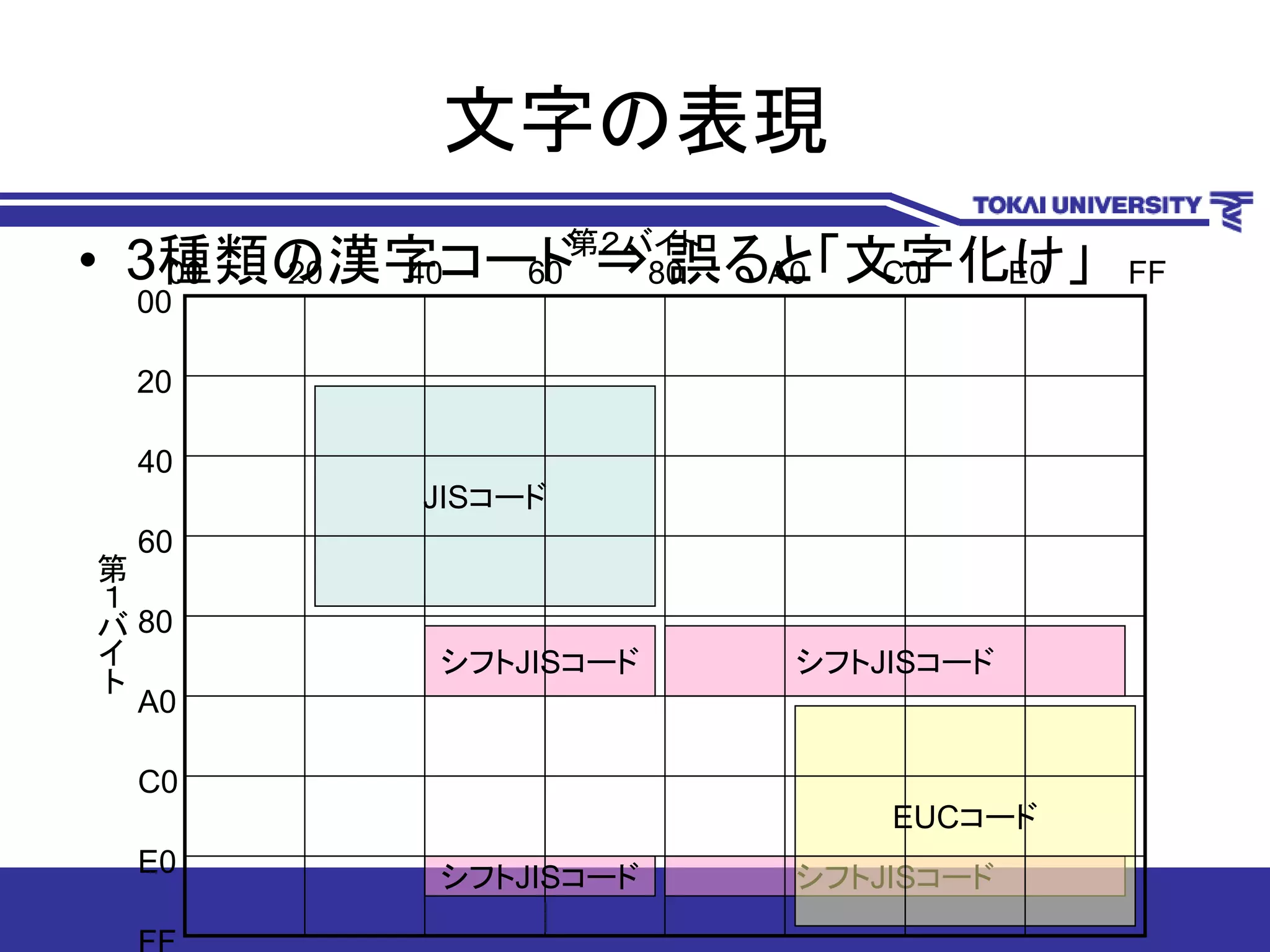
• 3種類の漢字コード ⇒ 誤ると「文字化け」
JISコード
第
１
バ
イ
ト
第２バイト
シフトJISコード シフトJISコード
シフトJISコード シフトJISコード
EUCコード
20
00
40
60
80
A0
C0
E0
2000 40 60 80 A0 C0 E0 FF

19. おまけ
4バイト整数型変数の最大値と最小値
• 最大値
– (0 111 1111 1111 1111 1111 1111 1111 1111)2
– (7f ff ff ff)16
– 2147483647
• 最小値
– (1 000 0000 0000 0000 0000 0000 0000 0000)2
– (80 00 00 00)16
– - 2147483648

20. おまけ
4バイト実数型変数の
絶対値の最大値と最小値
• 最大値
– (0 11111110 11111111111111111111111)2
– 7f ff ff ff
– (-1)0×2(254-127)×(1+ 1)
– 3.402824e+38
• 最小値
– (0 00000000 00000000000000000000001)2
– 00 00 00 01
– (-1)0×2(-126)×(0+1.192093e-07)
– 1.401299e-45 E=255でM≠0の場合⇒非数(NaN)
E=0でM≠0の場合⇒仮数部を1.XXXとせず
.XXXとして2-126を使う