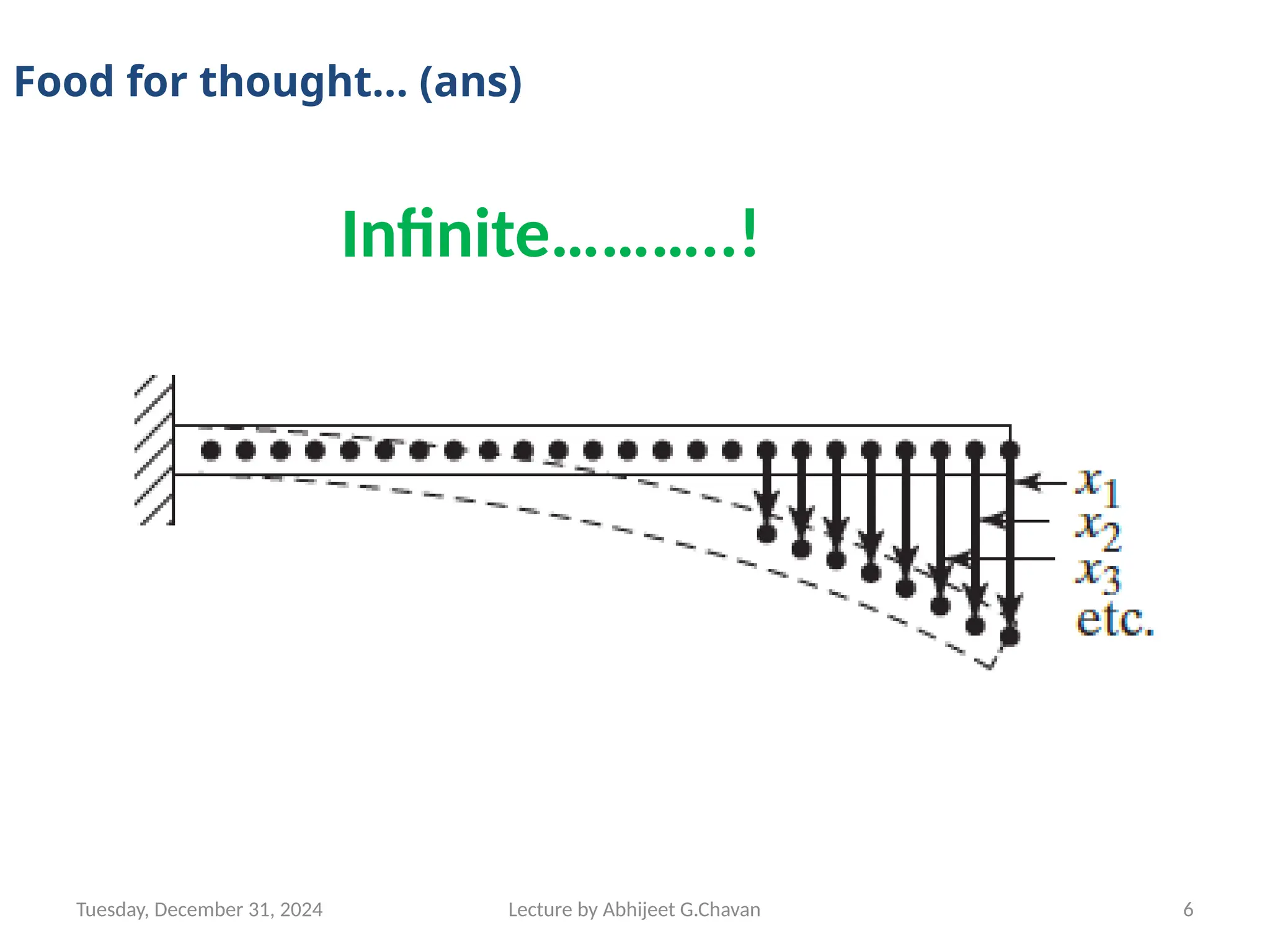
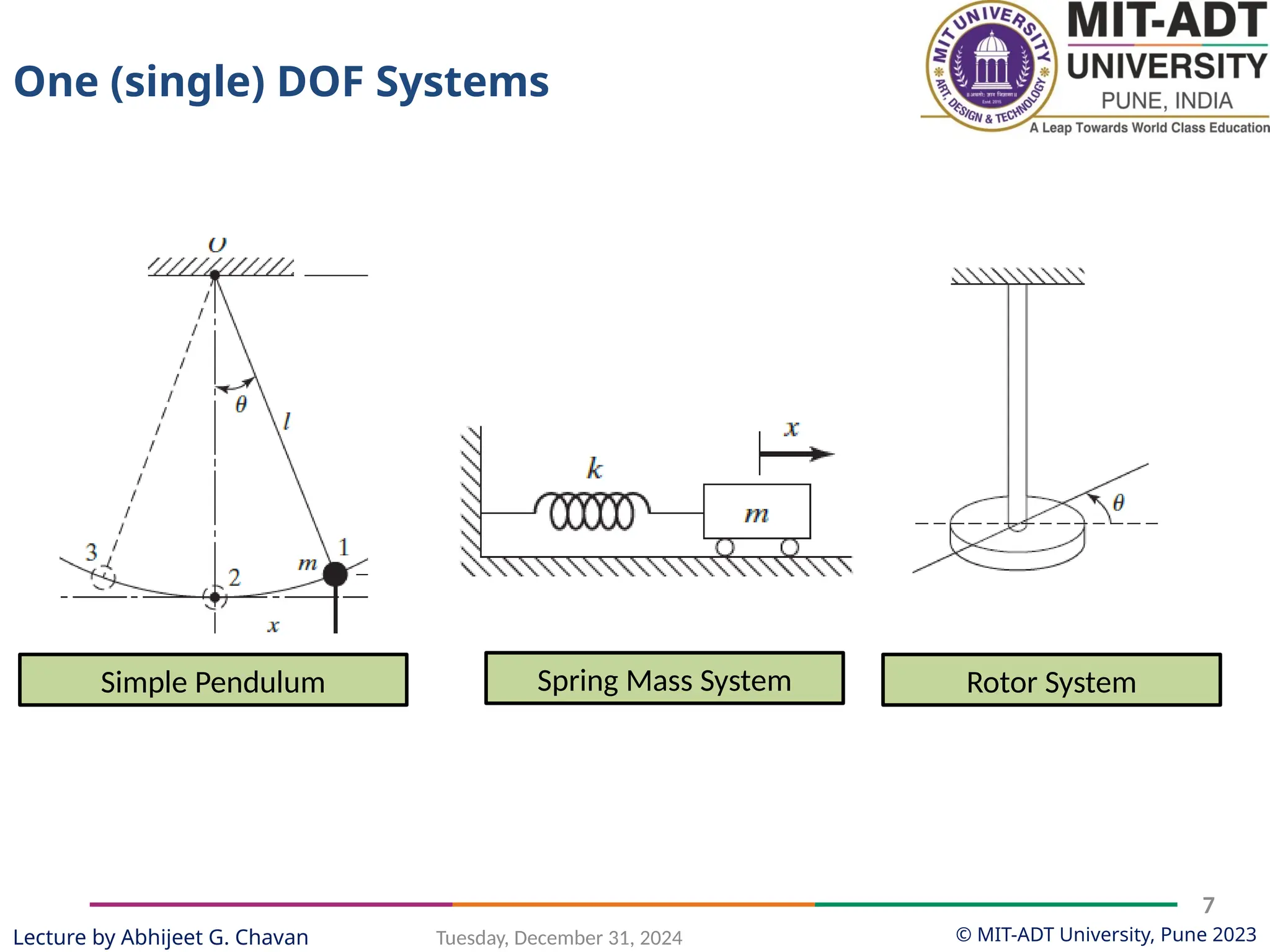
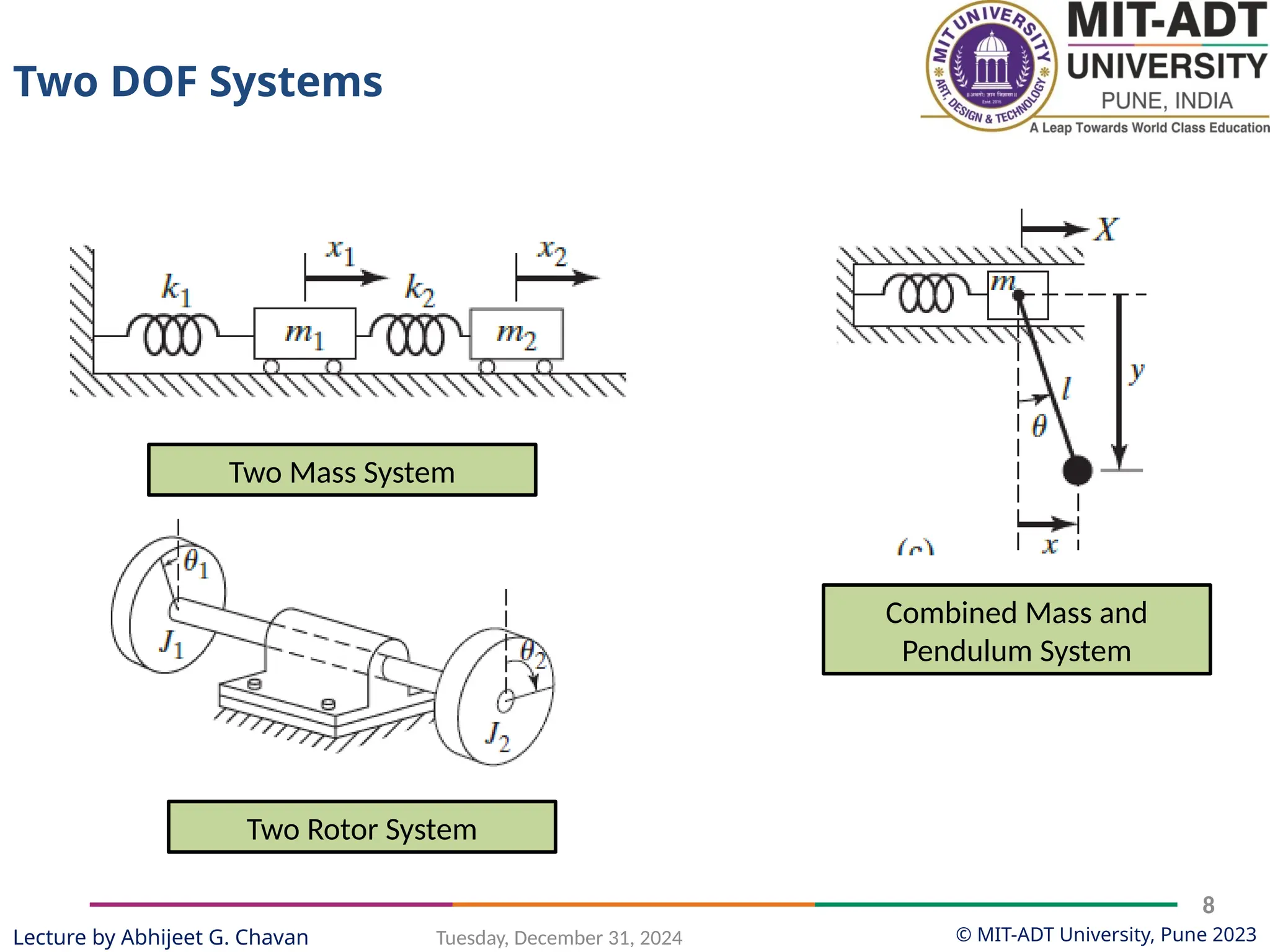
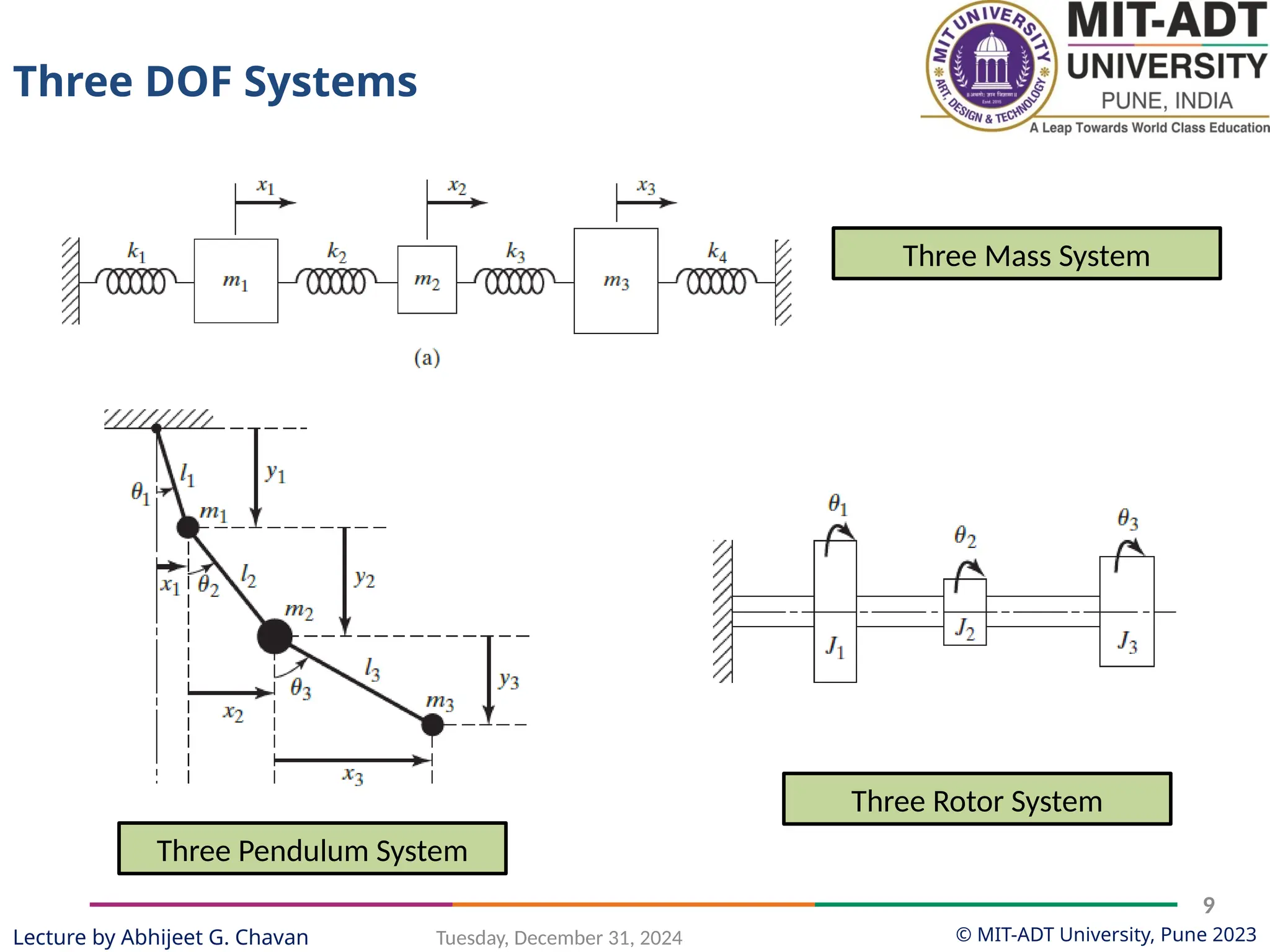
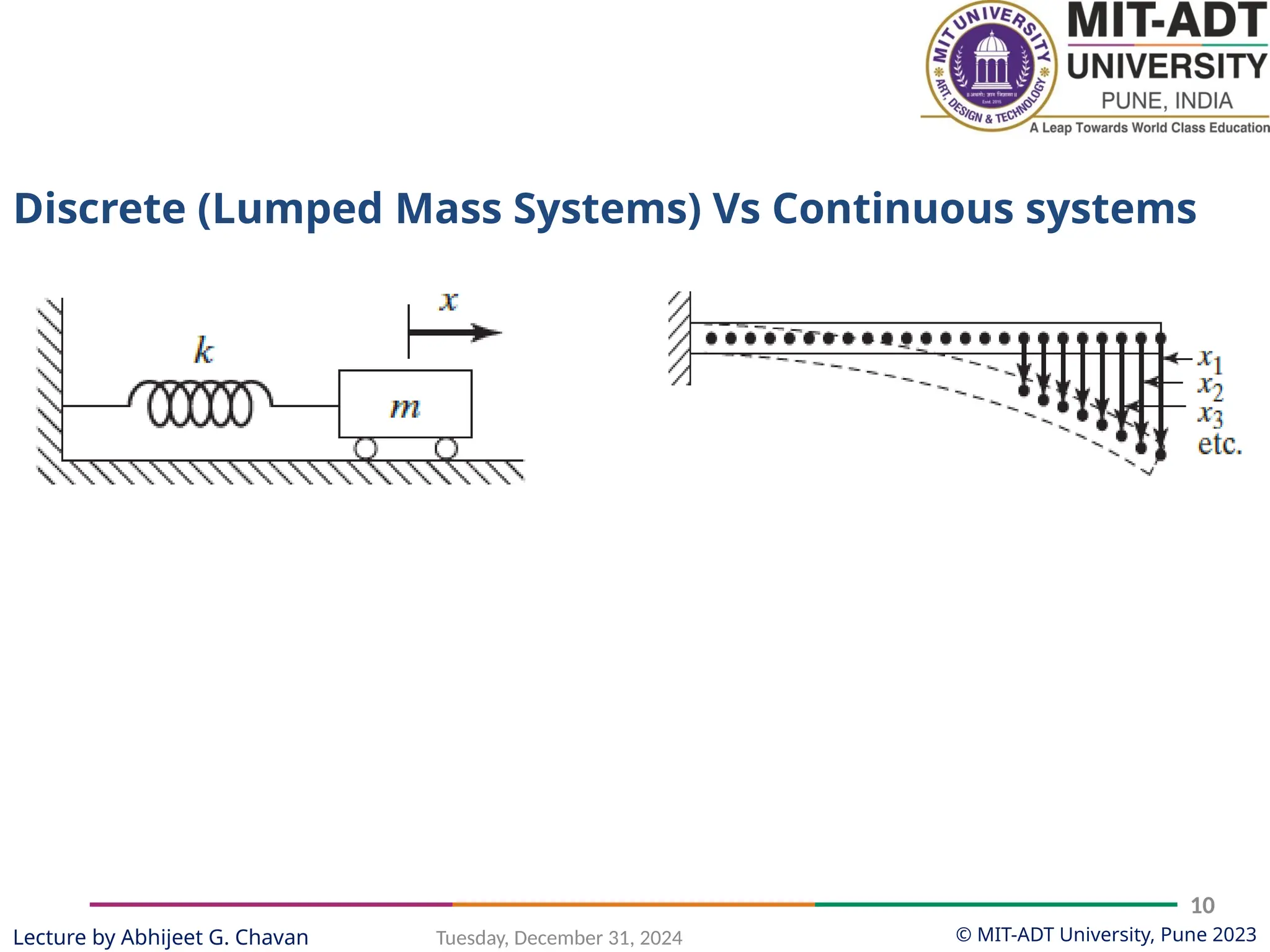
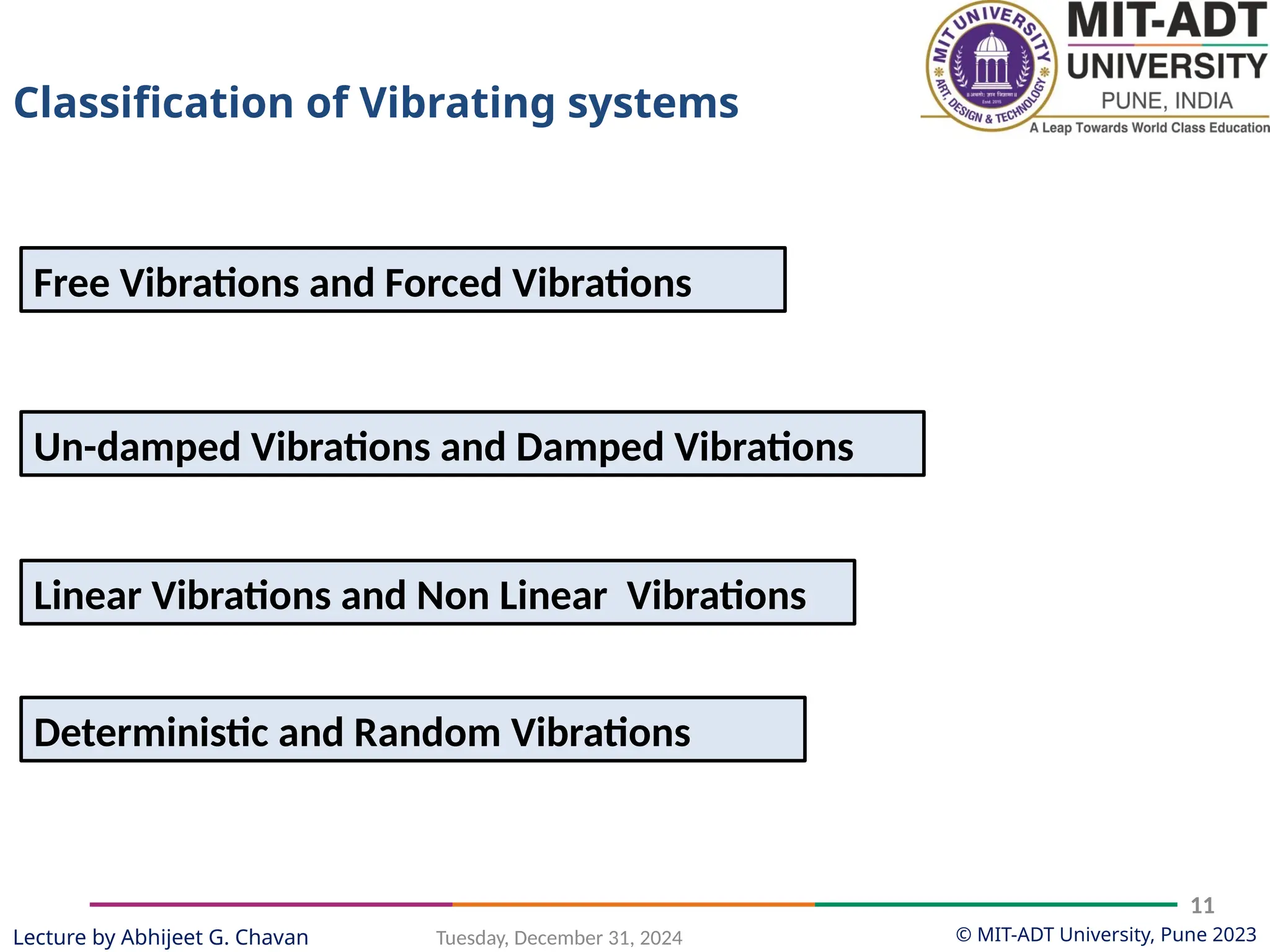
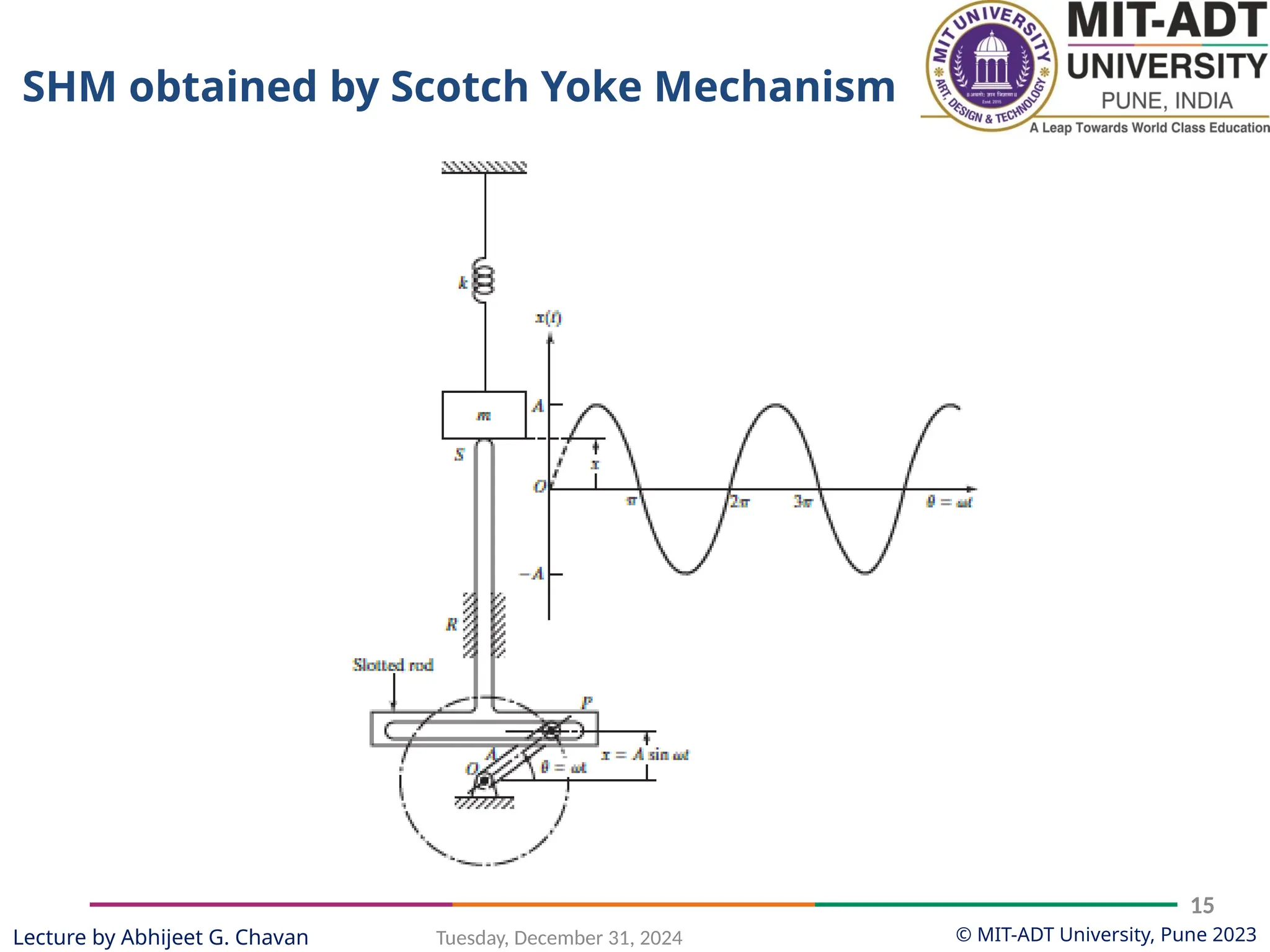
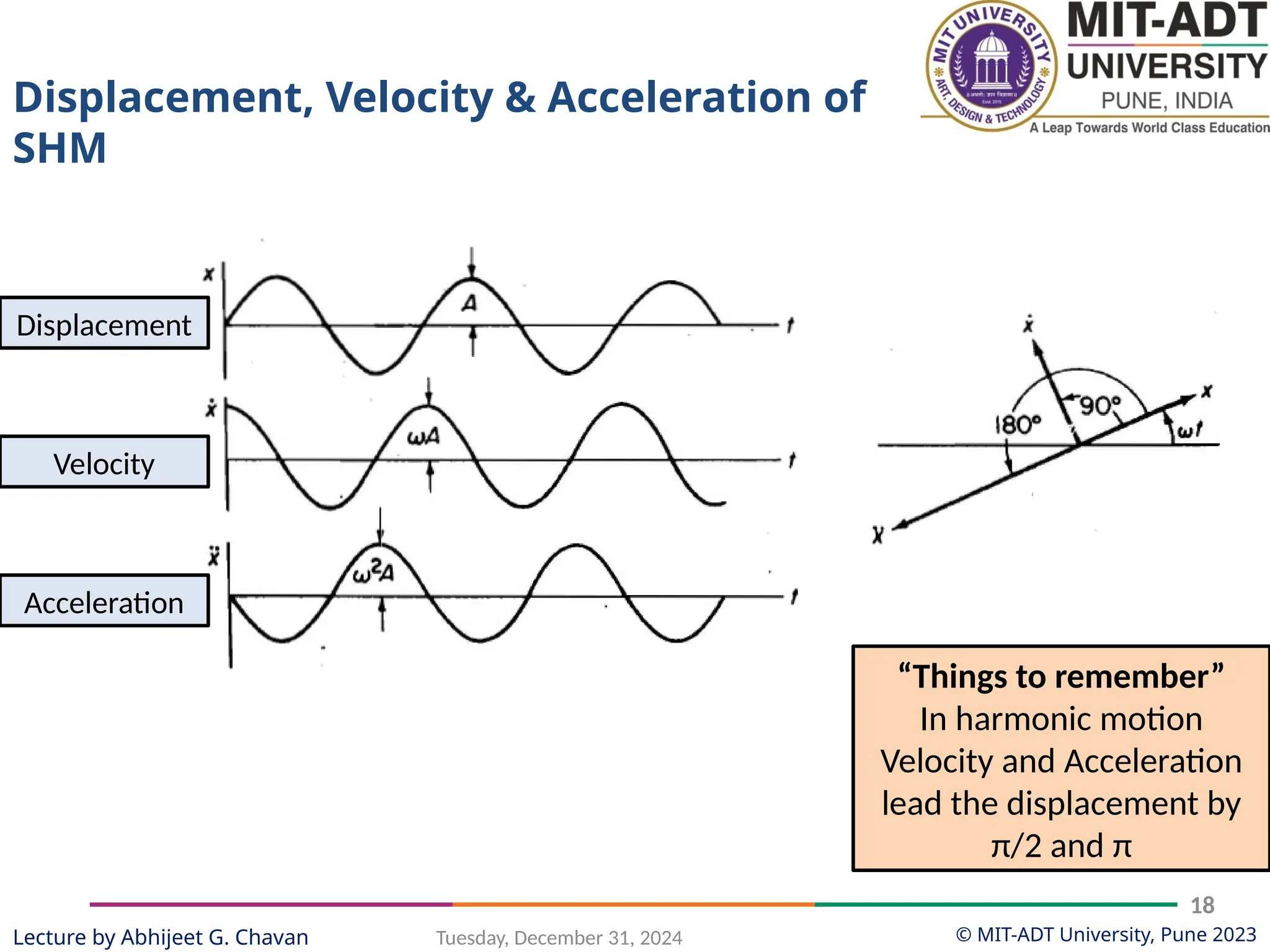
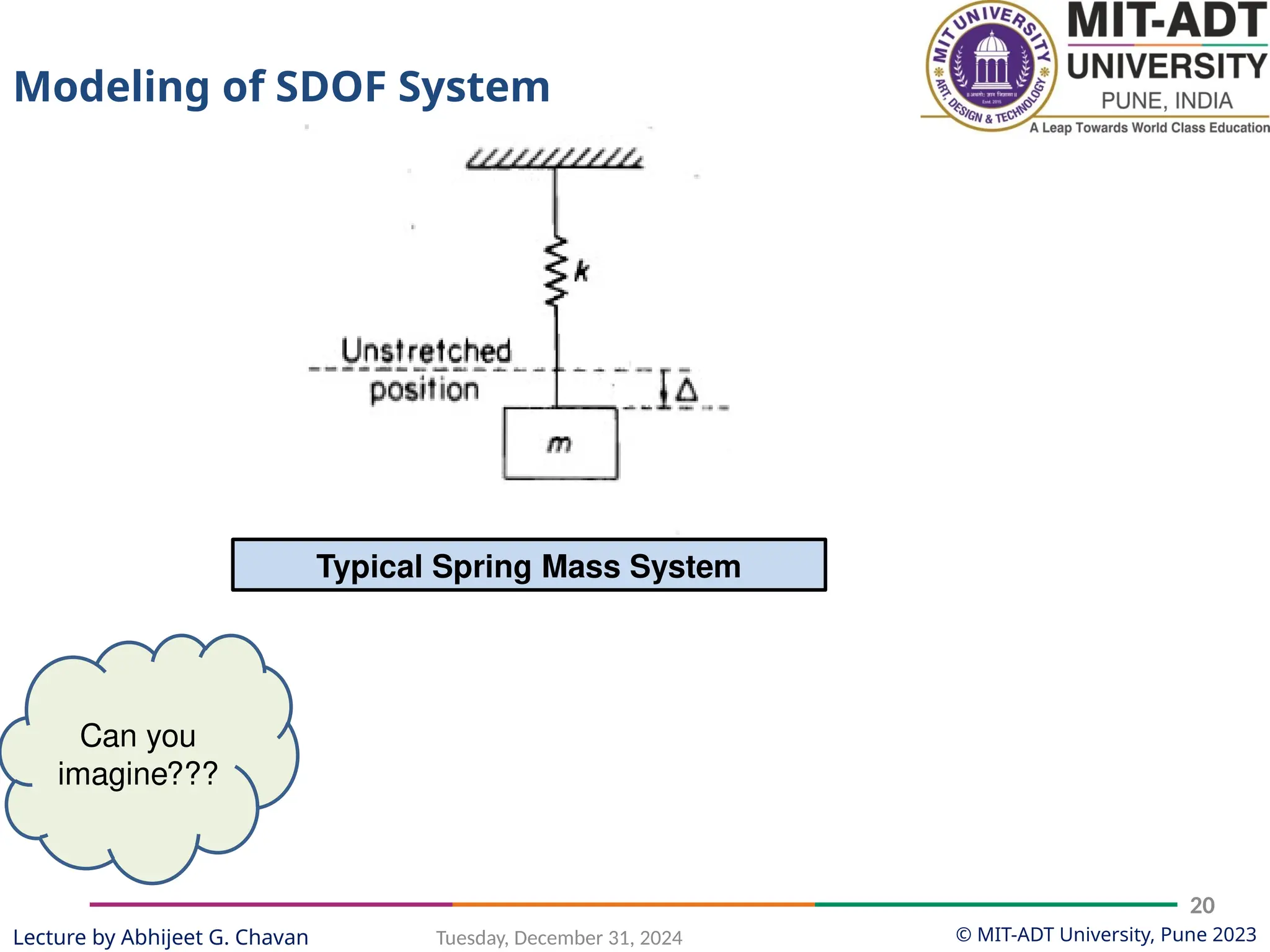
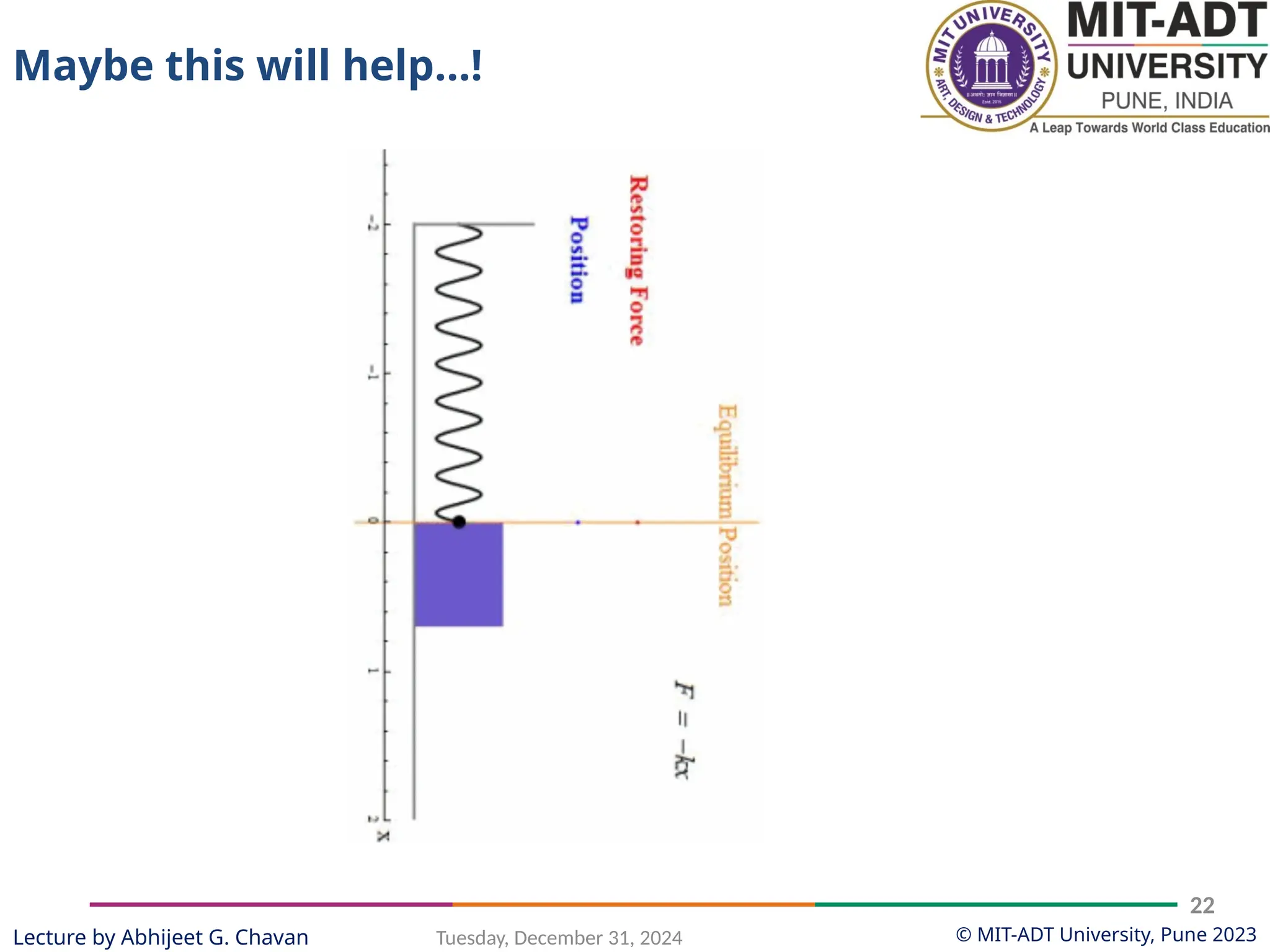
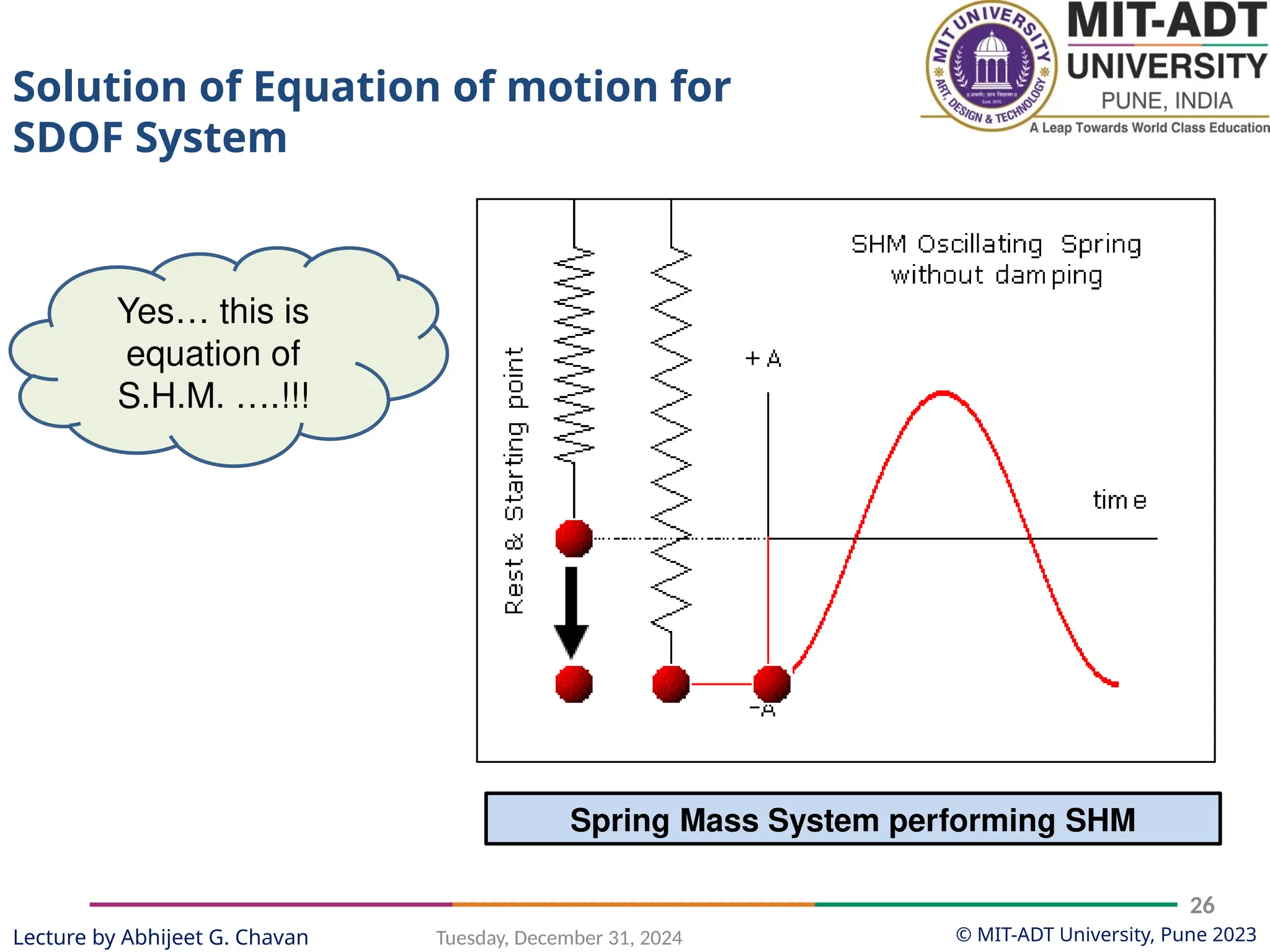
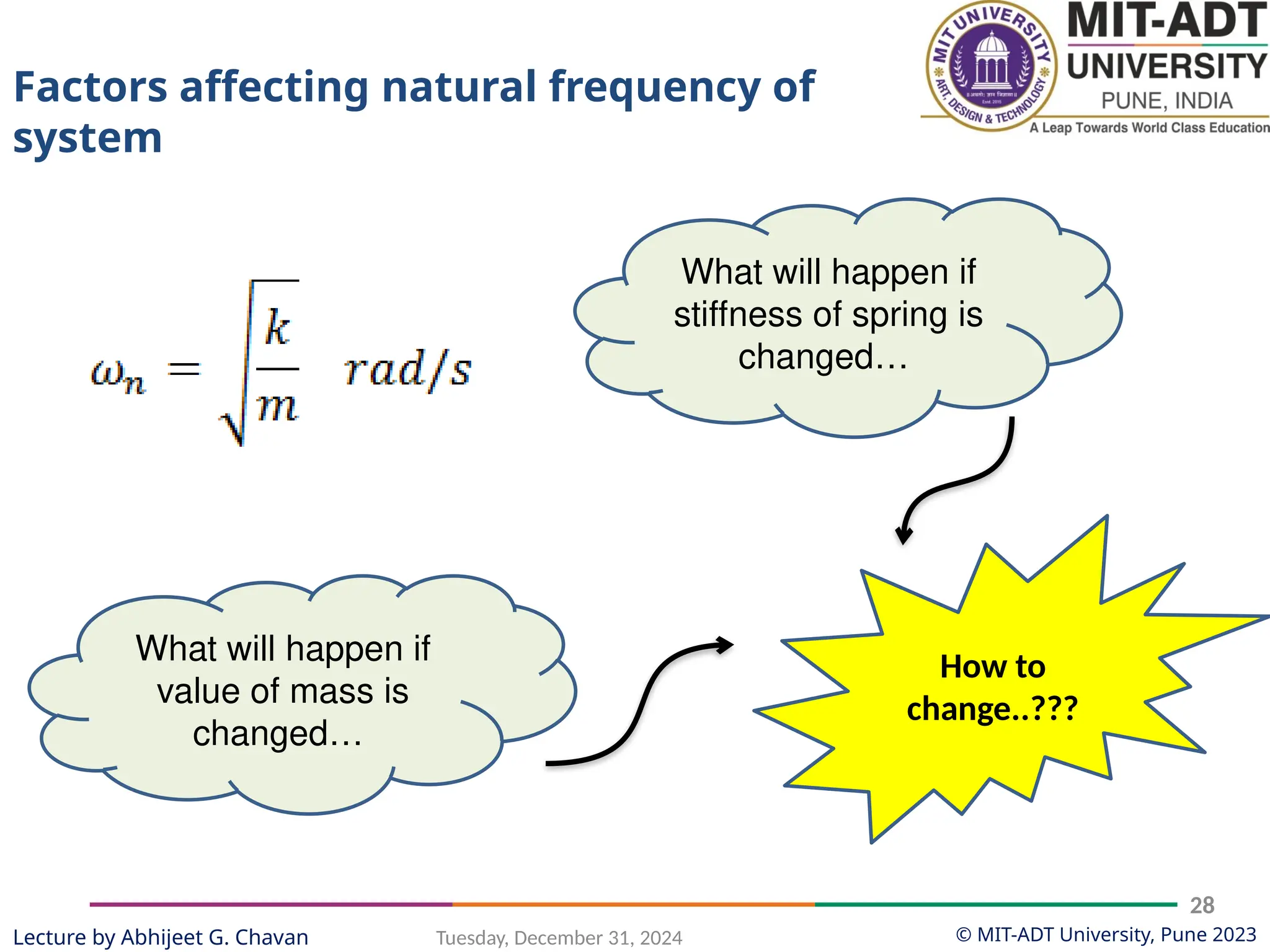
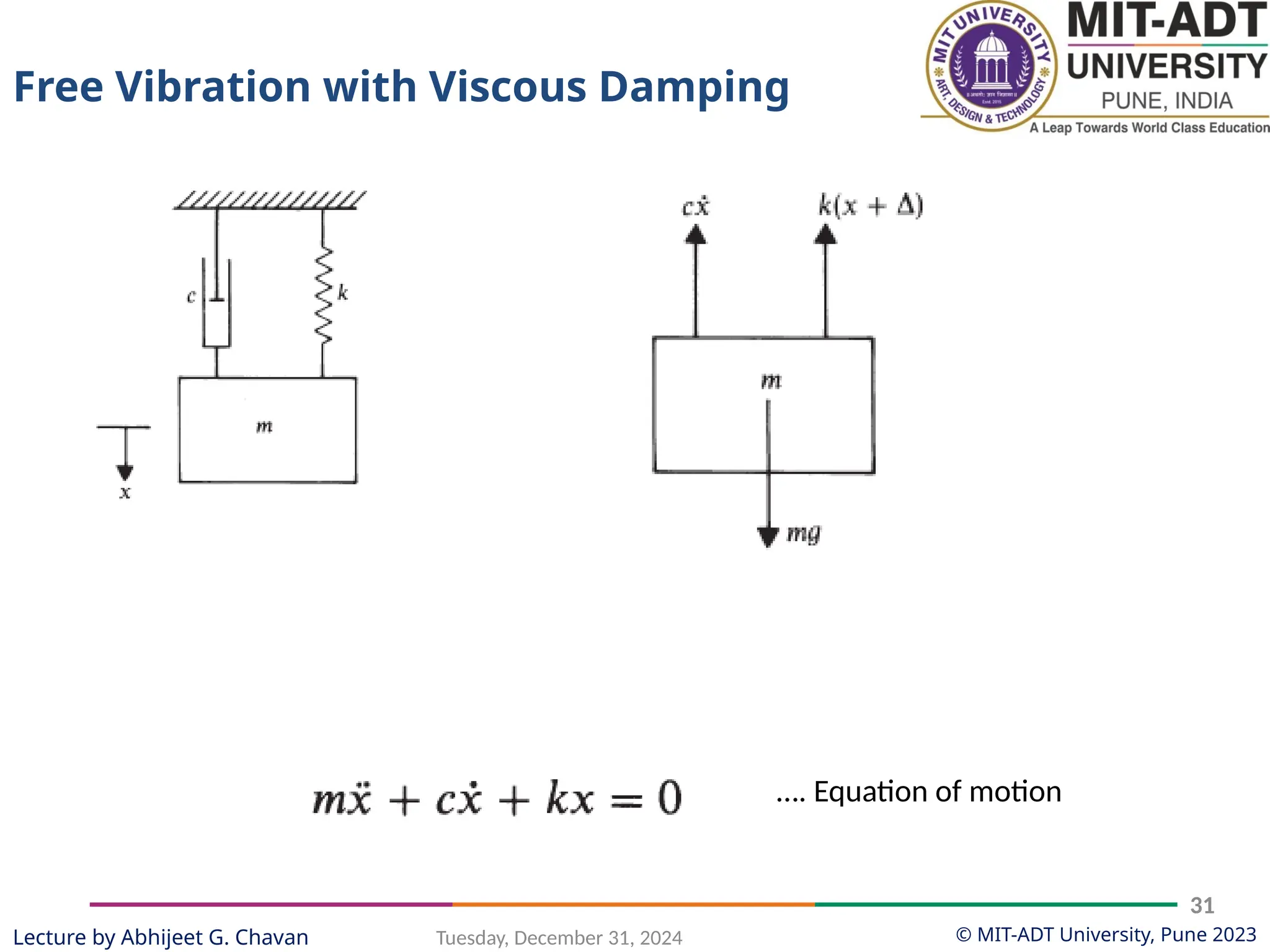
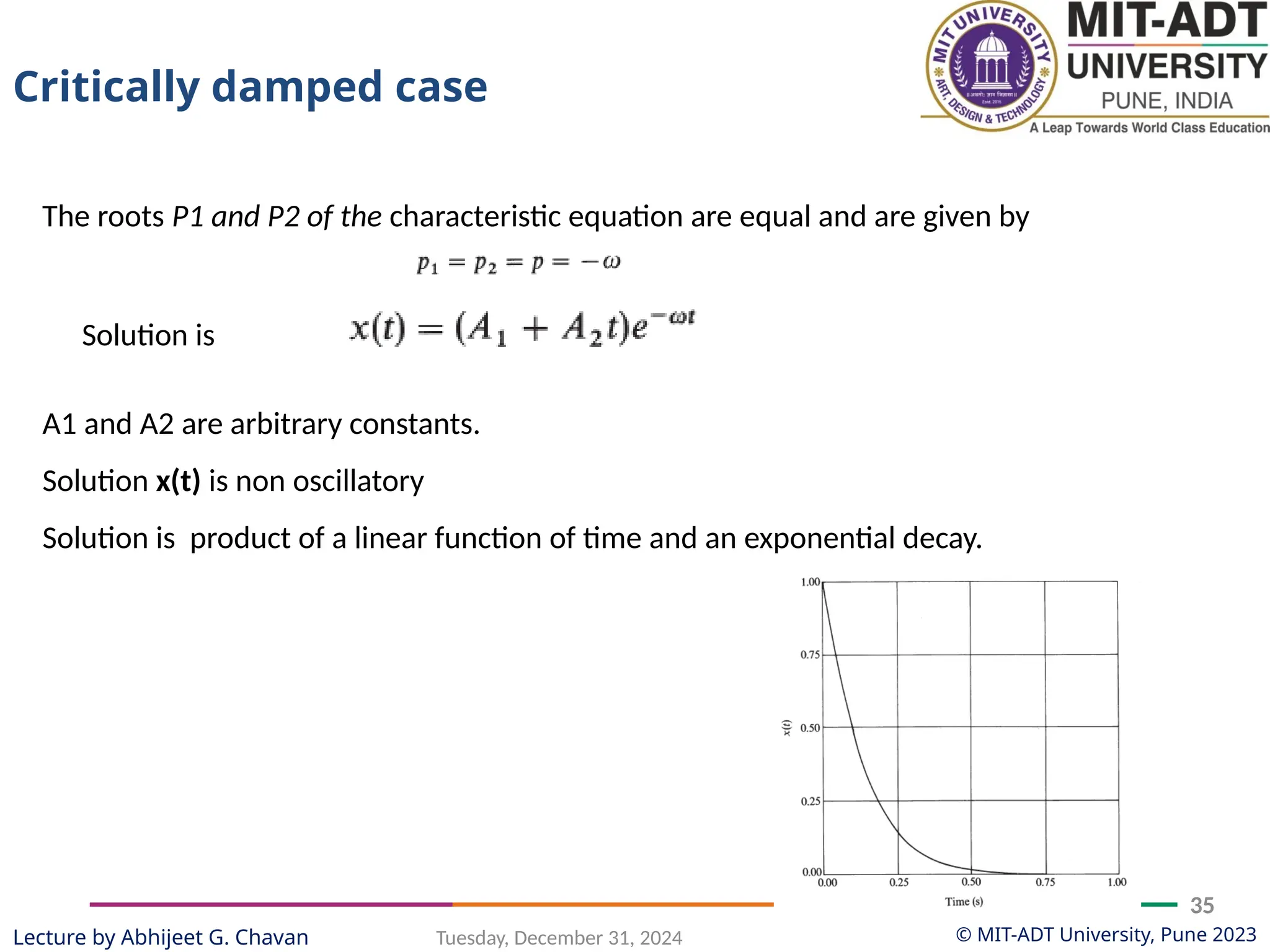
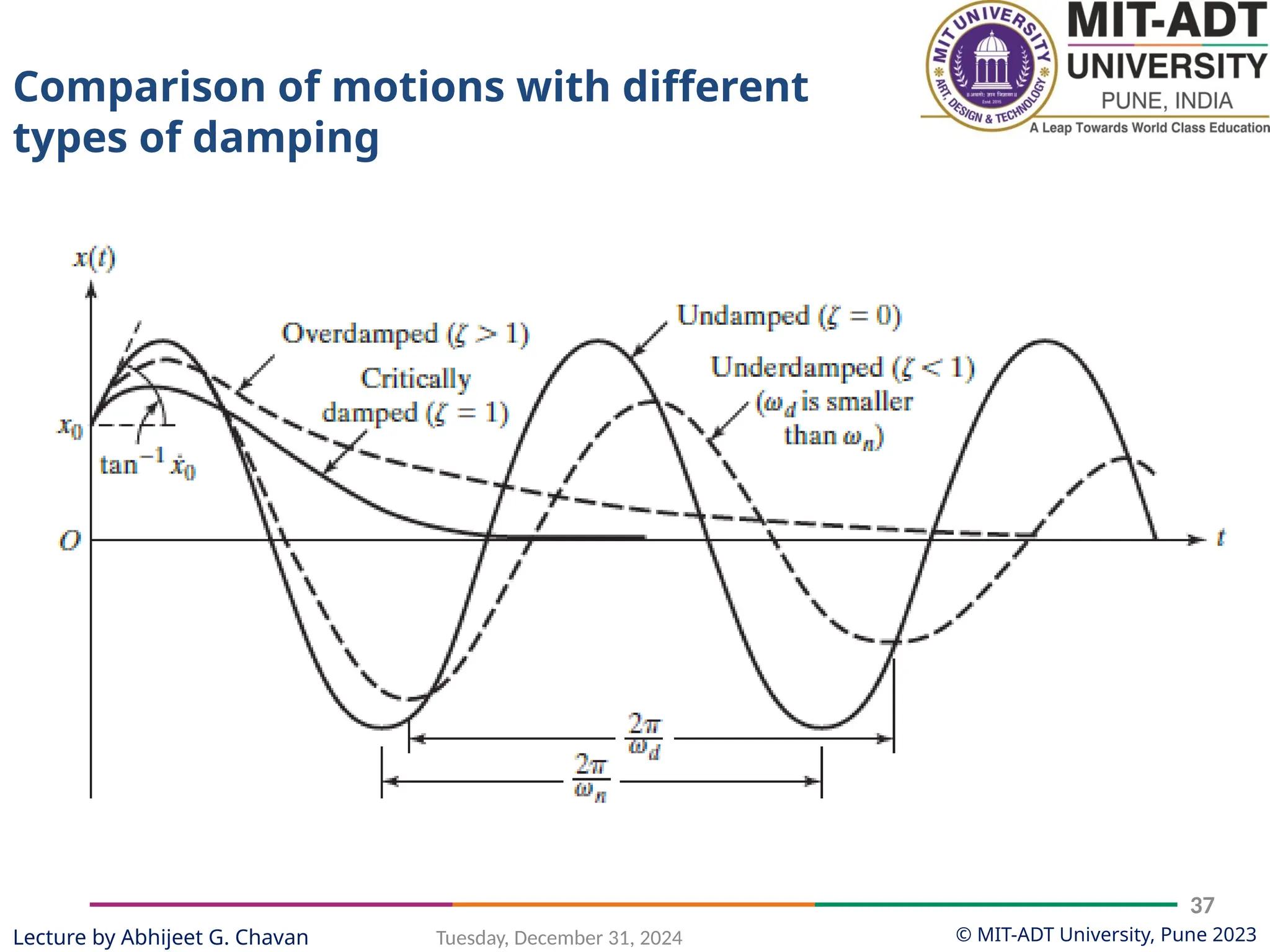
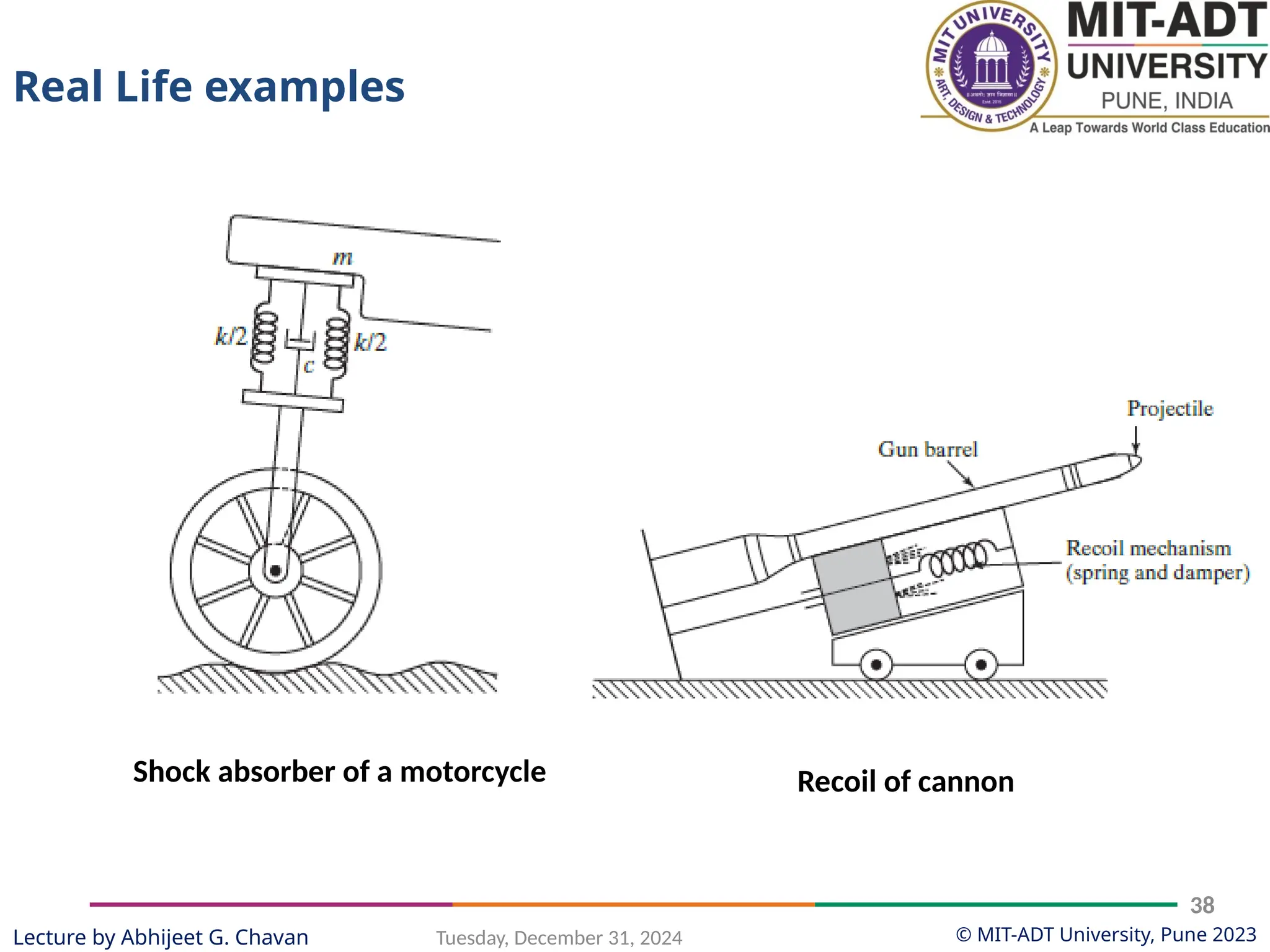
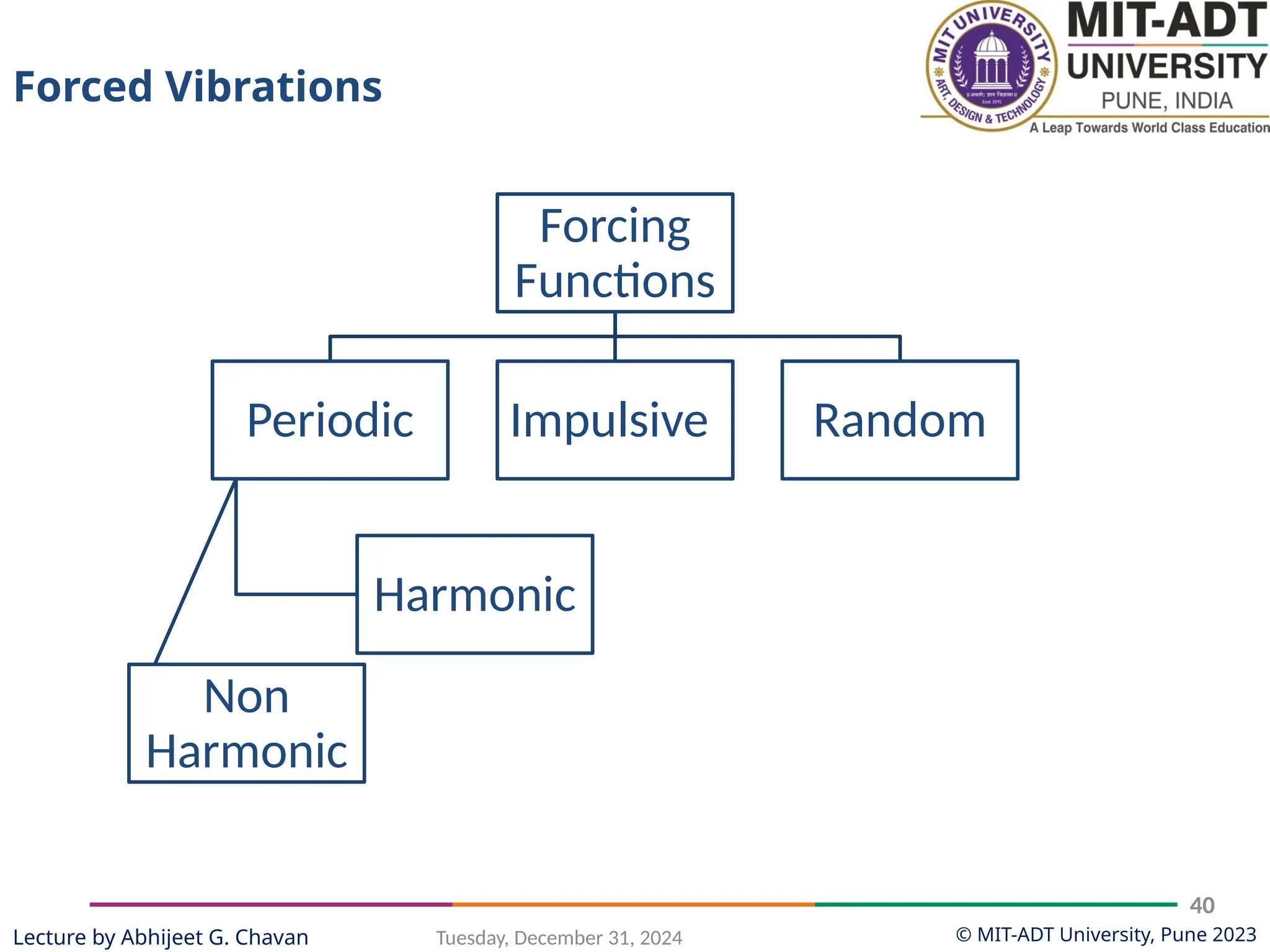
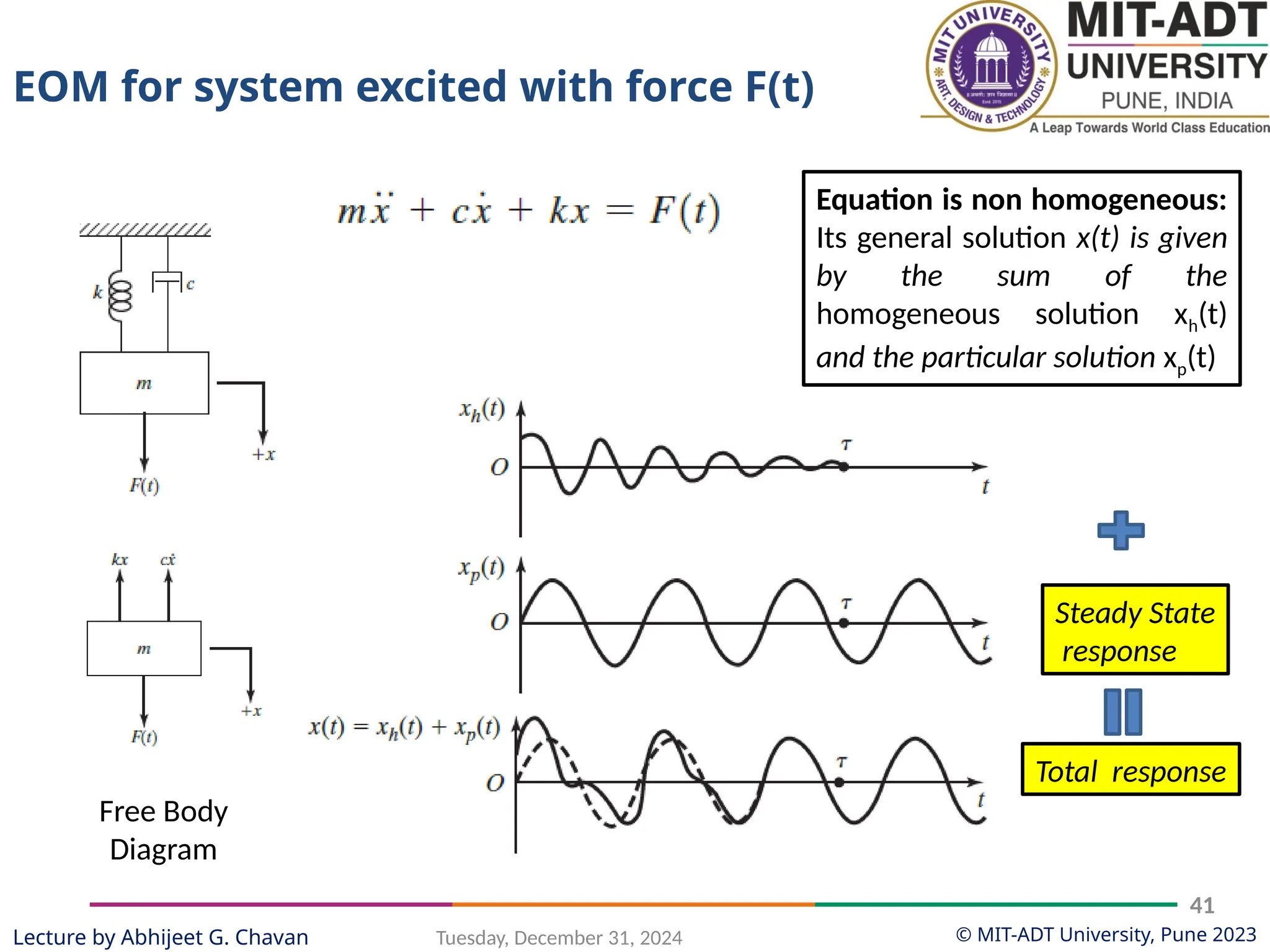
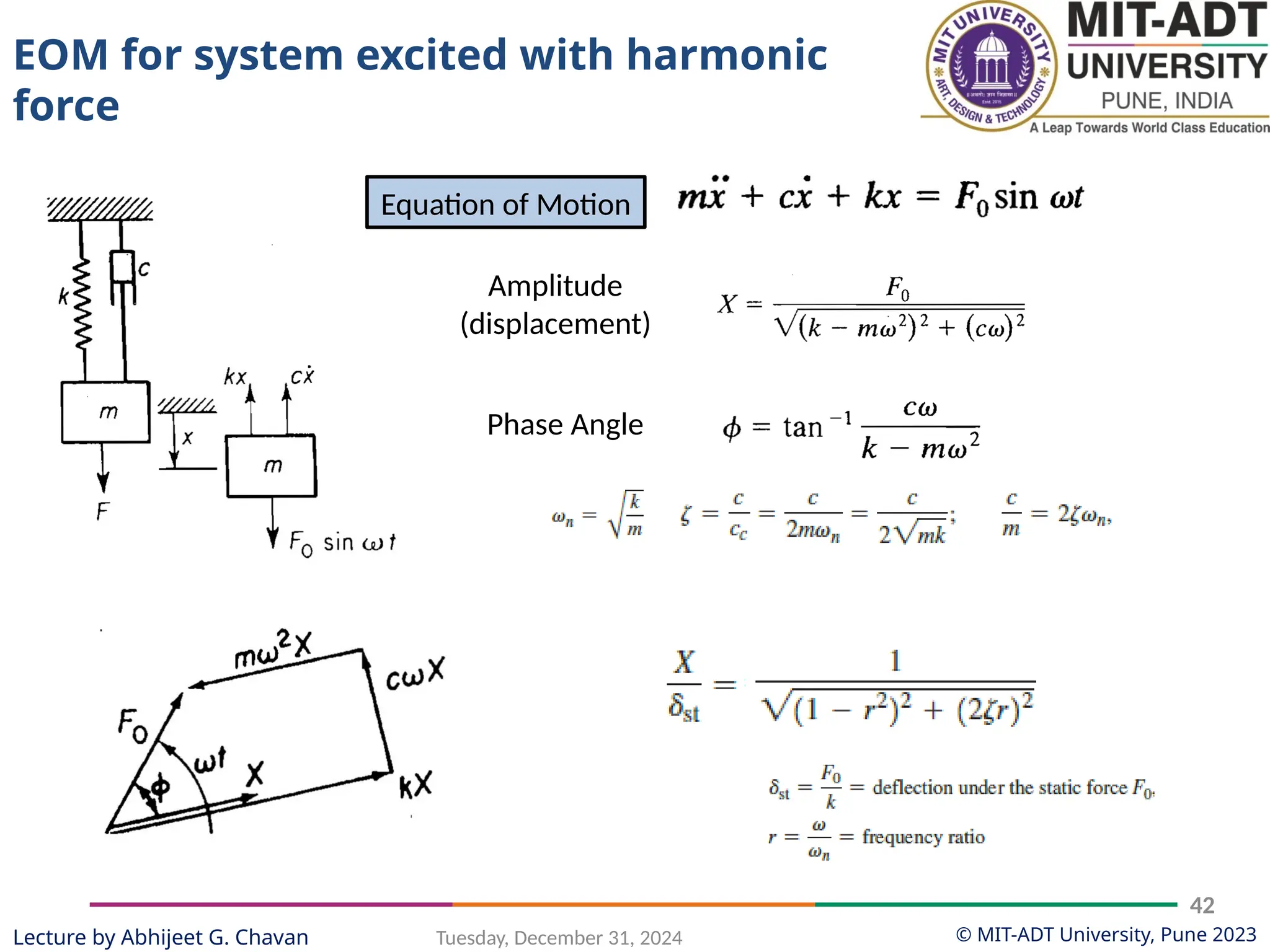
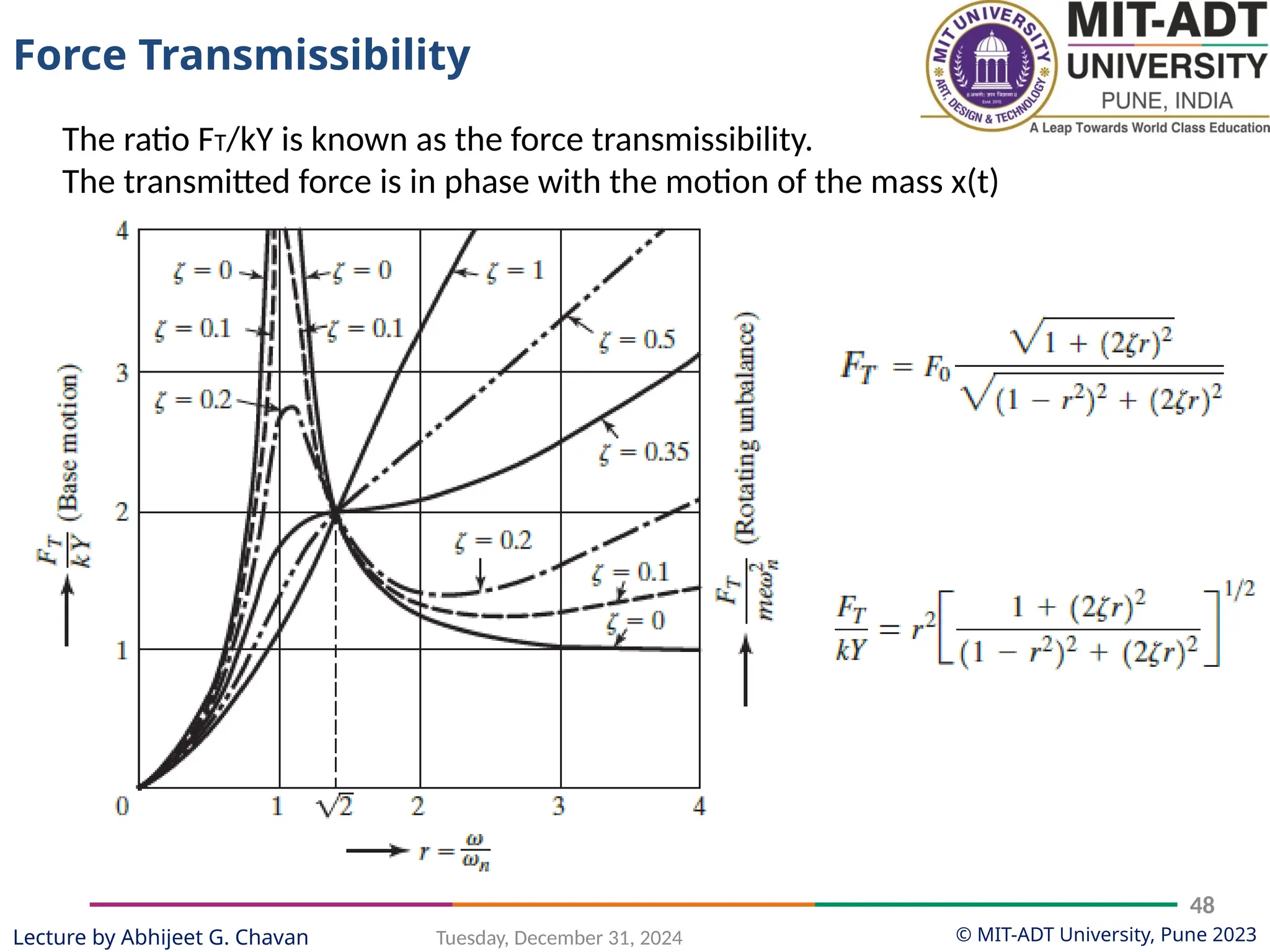
The document outlines a lecture series by Prof. Abhijeet G. Chavan at MIT ADT University on noise, vibration, and harshness (NVH) in electric vehicles, covering topics such as natural vibrations, damping, forced vibrations, and various types of vibrating systems. It provides a detailed breakdown of concepts including degrees of freedom, parameters affecting natural frequency, and the classification of vibrations, along with real-life applications and examples. Additionally, it discusses damping types, equations of motion, and response characteristics for systems under different damping conditions.