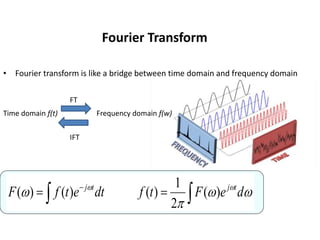
The document provides an overview of the Fourier transform, its implementation in Matlab, and its applications. The Fourier transform maps a function from its original domain (typically time) to the frequency domain. It has various uses including revealing hidden information, solving differential equations, and performing operations like convolution more easily in the frequency domain. Matlab functions for computing the Fourier transform numerically include FFT, IFFT, abs() to find the magnitude spectrum, and angle() to find the phase spectrum. An assignment involves implementing the Fourier transform in Matlab and analyzing effects of changes to the time domain signal and number of FFT points.

1. Tutorial-1
(Fourier Transform implementation in
Matlab )
EE-202 (Signal and systems)

2. Overview
• Introduction
• Fourier transform (FT)
• Relation between Fourier methods
• Basic Matlab code for FT
• References

3. Introduction
• Transform: A mathematical operation that takes a function or sequence
(one domain) and maps it into another one (other domain)
• We need signal transforms because
– The transform provides hidden information about the original function
or signal
– The transform helps to solve a differential equation
– The transform may provide data compression and storage may require
less memory
– Some operations may be easier to apply in the transform domain
(Example: Convolution operation in LTI systems).

4. • Fourier transform is like a bridge between time domain and frequency domain

 
 



 

d
e
F
t
f
dt
e
t
f
F t
j
t
j
)
(
2
1
)
(
)
(
)
(
Fourier Transform
Time domain f(t) Frequency domain f(w)
FT
IFT

5. Relation between Fourier methods
FFT is for implementation of DFT

6. Basic Matlab code for FT
• FFT- Fast Fourier transform (fast algorithm for implementation of discrete
Fourier transform). Y = fft(X,n,dim)
• IFFT- Inverse fast Fourier transform. X= ifft(Y,n,dim)
• abs()- Calculate magnitude of spectrum. mag = abs(fft(X,n,dim))
• angle()- Calculate phase of spectrum. phase = angle(fft(X,n,dim))

7. Assignment
• Solve one question numerically and also implement on Matlab.
• See the effect of change in amplitude in time domain signal on spectrum.
• Effect of number of FFT point.