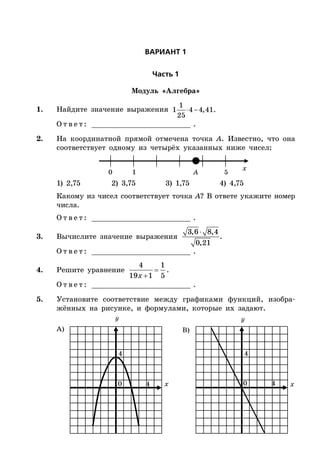
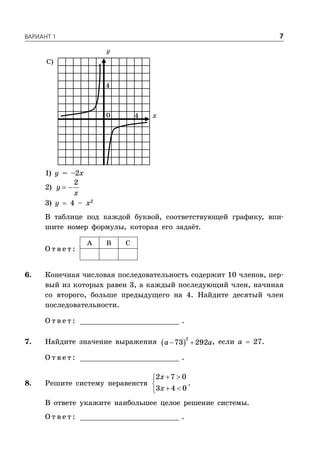
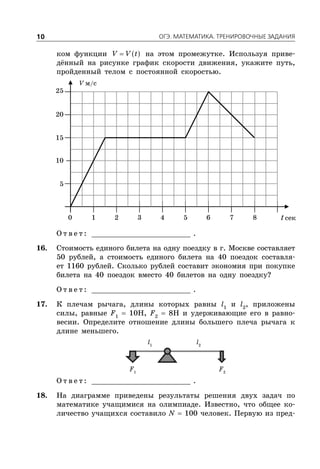
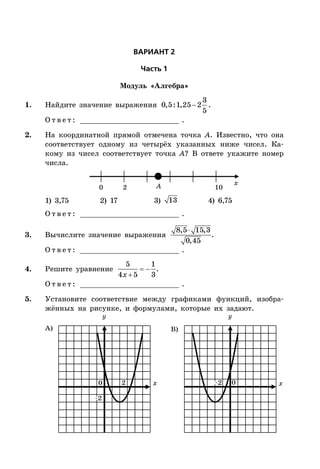
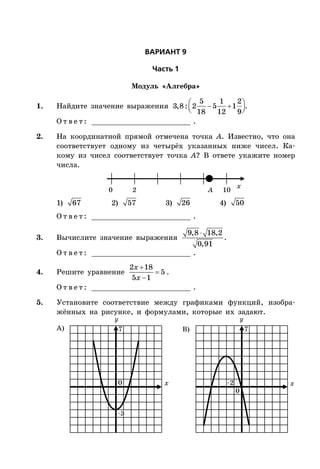
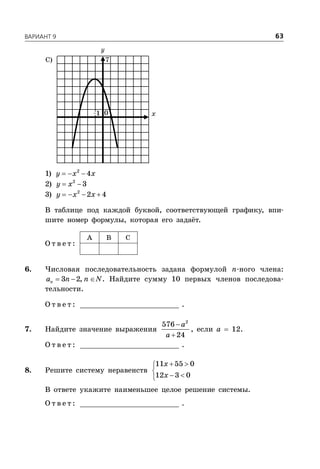
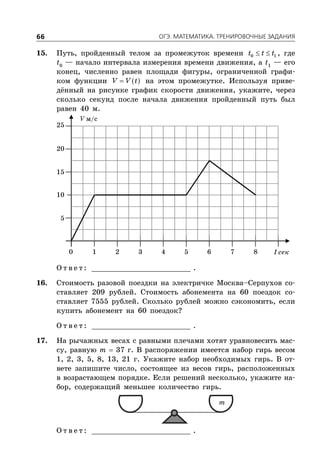
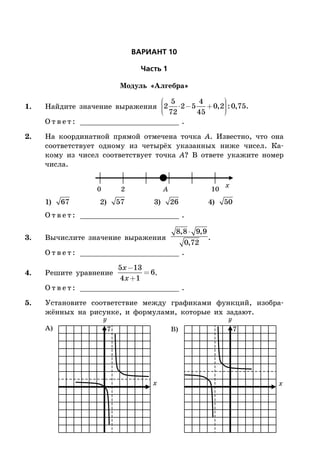
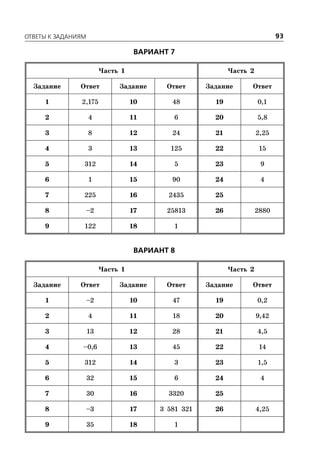
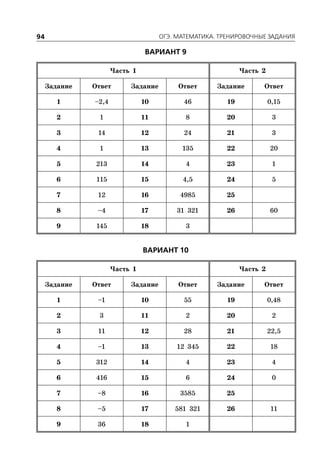
Документ представляет собой сборник заданий для подготовки к ОГЭ по математике на 2016 год, включая 10 вариантов с подробными решениями. Он охватывает три модуля: алгебру, геометрию и реальную математику, и предлагает советы по выполнению заданий для эффективной подготовки. В документе также представлены критерии оценки и требования для успешного прохождения экзамена.