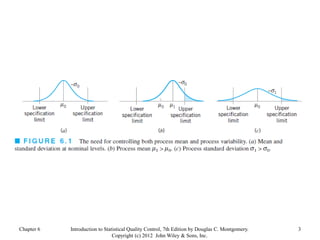
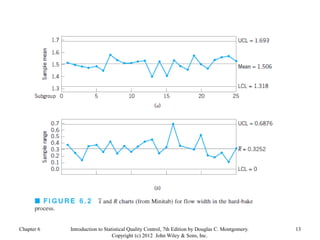
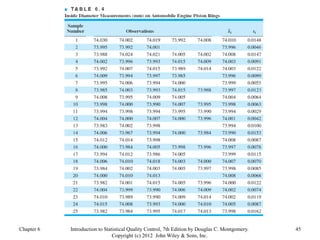
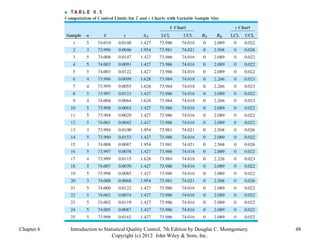
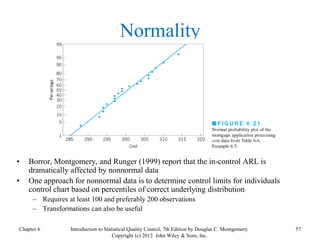
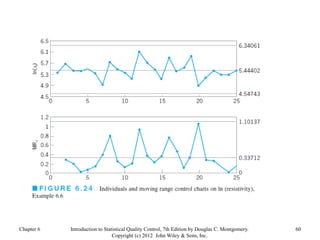
Chapter 6 of 'Introduction to Statistical Quality Control' by Douglas C. Montgomery discusses the use of control charts for monitoring process performance, including the calculation and revision of control limits based on subgroup data. It outlines the phases of control chart application, the distinction between control and specification limits, and guidelines for effective chart design. Additionally, it addresses the impact of non-normality on control chart performance and presents strategies for managing data variability.