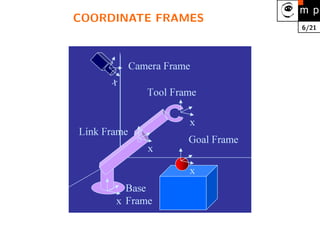
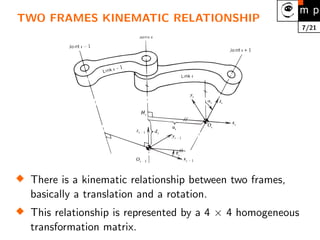
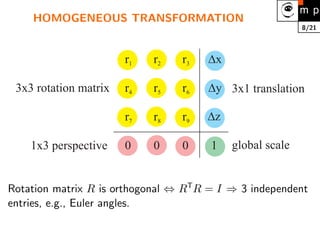
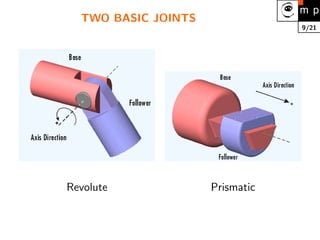
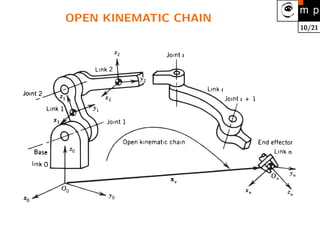
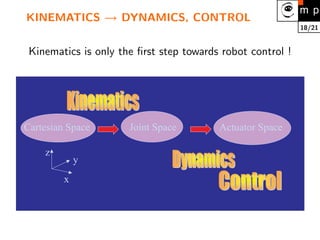
1. Robot kinematics is the analytical study of robot motion without considering forces or moments. It involves representing a robot as a series of rigid links connected by joints and determining the relationship between joint positions and the end effector position and orientation. 2. There are two main kinematic tasks: direct kinematics, which determines the end effector pose given joint positions, and inverse kinematics, which determines required joint positions to achieve a desired end effector pose. 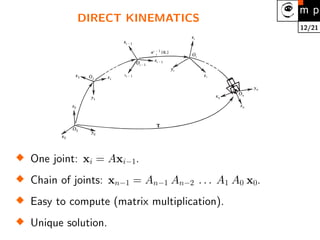3. Direct kinematics involves matrix multiplications to transform between reference frames. Inverse kinematics is more difficult and involves solving nonlinear equations, which may have multiple or no solutions. Simplifications like decoupling subproblems can help.

1. 1/21
ROBOT KINEMATICS
Václav Hlaváč
Czech Technical University, Faculty of Electrical Engineering
Department of Cybernetics, Center for Machine Perception
121 35 Praha 2, Karlovo nám. 13, Czech Republic
hlavac@fel.cvut.cz, http://cmp.felk.cvut.cz
LECTURE PLAN
1. Kinematics, what is?
2. Open, closed kinematic mechanisms.
3. Sequence of joint transformations (matrix multiplications)
4. Direct vs. inverse kinematic task.

2. 2/21
KINEMATICS
KINEMATICS – the analytical study of the geometry of
motion of a mechanism:
• with respect to a fixed reference co-ordinate system,
• without regard to the forces or moments that cause
the motion.
In order to control and programme a robot we must have
knowledge of both its spatial arrangement and a means of
reference to the environment.

3. 3/21
OPEN CHAIN MANIPULATOR KINEMATICS
Mechanics of a manipulator can be
represented as a kinematic chain
of rigid bodies (links) connected by
revolute or prismatic joints.
One end of the chain is constrained
to a base, while an end effector is
mounted to the other end of the
chain.
The resulting motion is obtained
by composition of the elementary
motions of each link with respect to
the previous one.

4. 4/21
CLOSED KINEMATIC CHAIN
Much more difficult.
Even analysis has to take into account statics, constraints
from other links, etc.
Synthesis of closed kinematic mechanisms is very difficult.

5. 5/21
KINEMATICS vs. DIFFERENTIAL KINEMATICS
Kinematics describes the analytical relationship between
the joint positions and the end-effector position and
orientation.
Differential kinematics describes the analytical relationship
between the joint motion and the end-effector motion in
terms of velocities.

6. 6/21
COORDINATE FRAMES

7. 7/21
TWO FRAMES KINEMATIC RELATIONSHIP
There is a kinematic relationship between two frames,
basically a translation and a rotation.
This relationship is represented by a 4 × 4 homogeneous
transformation matrix.

8. 8/21
HOMOGENEOUS TRANSFORMATION
r1 r3
r4 r5 r6
r7 r8 r9
r2
0
0
0 1
Dx
Dy
Dz
3x3 rotation matrix 3x1 translation
global scale
1x3 perspective
Rotation matrix R is orthogonal ⇔ RT
R = I ⇒ 3 independent
entries, e.g., Euler angles.

9. 9/21
TWO BASIC JOINTS
Revolute Prismatic

10. 10/21
OPEN KINEMATIC CHAIN

11. 11/21
DIRECT vs. INVERSE KINEMATICS
In manipulator robotics, there are two kinematic tasks:
Direct (also forward) kinematics – Given are joint relations
(rotations, translations) for the robot arm. Task: What is
the orientation and position of the end effector?
Inverse kinematics – Given is desired end effector position and
orientation. Task: What are the joint rotations and
orientations to achieve this?

12. 12/21
DIRECT KINEMATICS
One joint: xi = Axi−1.
Chain of joints: xn−1 = An−1 An−2 . . . A1 A0 x0.
Easy to compute (matrix multiplication).
Unique solution.

13. 13/21
INVERSE KINEMATICS
For a kinematic mechanism, the inverse kinematic problem
is difficult to solve.
The robot controller must solve a set of non-linear
simultaneous algebraic equations.
Source of problems:
• Non-linear equations (sin, cos in rotation matrices).
• The existence of multiple solutions.
• The possible non-existence of a solution.
• Singularities.

14. 14/21
INVERSE KINEMATICS, SIMPLIFICATIONS
Divide and conquer strategy. Decouple the problem into
independent subproblems.
The spherical wrist. Positioning of the wrist + positioning
within the wrist.
Design conventions, e.g. Denavit-Hartenberg systematic
frame assignment.

15. 15/21
MANIPULATOR KINEMATIC (1)
Cartesian Gantry

16. 16/21
MANIPULATOR KINEMATIC (2)
Cylindrical Sphere

17. 17/21
MANIPULATOR KINEMATIC (3)
SCARA Anthropomorphic

18. 18/21
KINEMATICS → DYNAMICS, CONTROL
Kinematics is only the first step towards robot control !
Cartesian Space Joint Space Actuator Space
z
y
x

19. 19/21
CLOSED PARALLEL CHAIN
Hexamod

20. 20/21
REAL HEXAMOD (1)

21. 21/21
REAL HEXAMOD (2)