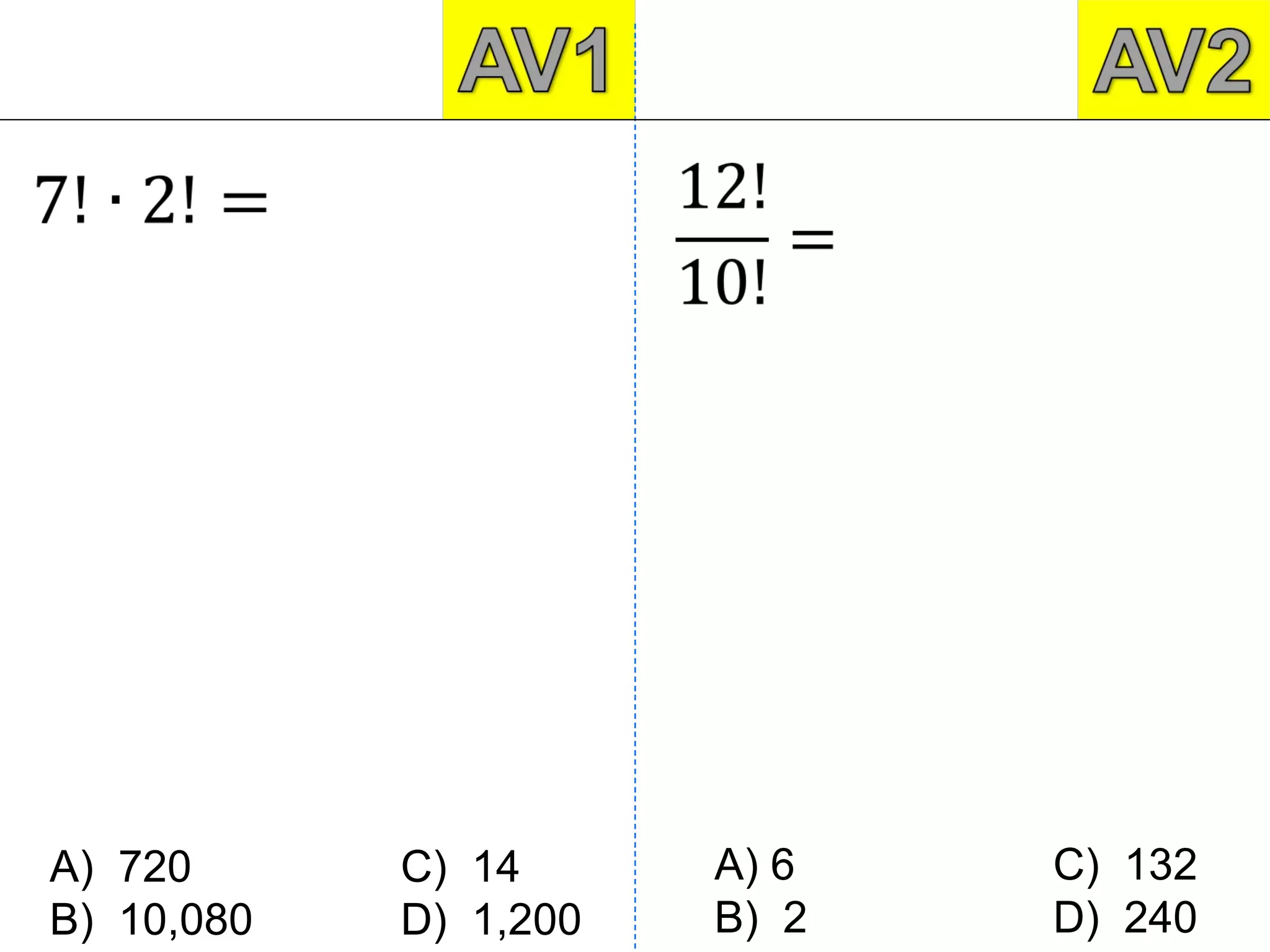
The document provides an agenda for an Algebra 2 class that includes: 1) An opener for 5 minutes, learning objective 10.1, and assignment #2. 2) Materials needed include activotes and reminders of an upcoming Chapter 10 test. 3) Learning objective 10.1 introduces permutations, defined as arrangements of distinct objects in a specific order, with the number of permutations calculated as n factorial or n! for n objects. 4) An example is provided to distinguish permutations with and without repetition.

1. Opener: Agenda (Algebra 2)
•Opener (5 mins)
The digits 1, 2, 3, 4, 5, 6 and 7 are used to generate a •LE 10.1
Four-digit customer code. How many different •Assignment #2
codes are possible if the first two digits must be
even numbers and the last two digits must be odd
numbers and repetition is allowed?
Materials Needed
•activotes
Reminders
•Ch.10 Test scheduled
for Mar 30
A+M=P:

2. LE 10.1 Introduction of Permutation
WofD:n factorial,
LO: What is a permutation? permutation
An arrangement of n distinct objects in
a specific order is called a permutation.
The number of ways to arrange:
•n objects using ALL n objects without
repetitions is n!
•n objects using ALL n objects with
repetitions is
n!
s!⋅s! s!
NOTE: This is also referred to as
By definition: distinguishable permutation
0! = 1 (with reps)

3. A) 720 C) 14 A) 6 C) 132
B) 10,080 D) 1,200 B) 2 D) 240

4. Model Skill “I DO” Scaffold Skill “WE DO”
Example: Example
How many ways can I arrange 5 students In how many different ways can 4 teams
finish a competition (assuming there are
in line?
no ties)?
Solution:
Solution
Method 1: FCP
___ x ___ x ___ x ___ x ___
S1 S2 S3 S4 S5
Method 2: Permutation

5. Guided Practice “YOU DO”
Example
You need to arrange seven of your favorite books along a small shelf. How many
different ways can you arrange the books, assuming that the order of the books
makes a difference to you?
A) 5040 B) 7 C) 823,543 D) 840

6. Model Skill “I DO” Scaffold Skill “WE DO”
Example: Example
How many different ways can the letters How many different ways can the letters
in MATH be arranged? in MISSISSIPPI be arranged?
Solution: Solution

7. Guided Practice “YOU DO”
Example
How many 3 digit numbers can be formed using only odd digits from 1 through 9,
with repetition allowed?
A) 15 B) 7 C) 27 D) 125

8. Guided Practice “YOU DO”
Example
You have 4 flower pots on a window seal, how many different ways can you arrange
the flower pots?
A) 4 B) 24 C) 256 D) 16