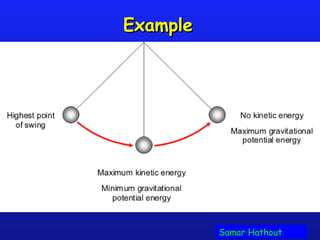
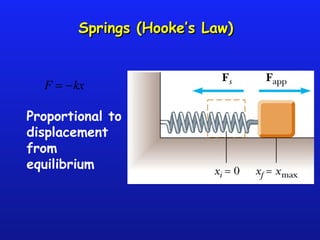
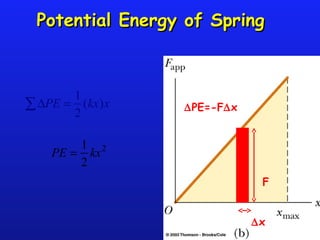
Work is the transfer of energy through motion caused by a force acting over a distance. The amount of work done depends on the force applied and the distance over which it acts. Work can be calculated using the formula Work=force x distance. Conservation of energy states that the total mechanical energy in a system remains constant if no non-conservative forces act. If non-conservative forces are present, they may change the total energy by doing work which transfers energy into other forms like heat. Springs obey Hooke's law, such that the force applied by a spring is proportional to its displacement from its resting length.

1. WORK AND CONSERVATIONWORK AND CONSERVATION
OF ENERGYOF ENERGY
STYMVERLY GAWAT
JENERUS JUAN
AND ALWEN AGYAM

2. Work is the transfer of energy through motion. In
order for work to take place, a force must be exerted
through a distance. The amount of work done depends
on two things: the amount of force exerted and the
distance over which the force is applied. There are
two factors to keep in mind when deciding when work
is being done: something has to move and the motion
must be in the direction of the applied force. Work
can be calculated by using the following formula:
Work=force x distance
WorkWork

3. Work is done on the
books when they are
being lifted, but no
work is done on
them when they are
being held or
carried horizontally.
WorkWork

4. Work can be positive orWork can be positive or
negativenegative
• Man does positive work
lifting box
Man does negative work
lowering box
Gravity does positive work
when box lowers
Gravity does negative work
when box is raised

5. Work done by a constant ForceWork done by a constant Force
θ
∆Ekin = Wnet
• W = F s = |F| |s| cos θ = Fs s
|F| : magnitude of force
|s| = s : magnitude of displacement
Fs = magnitude of force in
direction of displacement :
Fs = |F| cos θ
θ: angle between displacement and force
vectors
• Kinetic energy : Ekin= 1/2 m v2
• Work-Kinetic Energy Theorem:
F
s

6. Conservation of Mechanical EnergyConservation of Mechanical Energy
Total mechanical energy of an object remains constant
provided the net work done by non-conservative forces
is zero:
Etot = Ekin + Epot = constant
or
Ekin,f+Epot,f = Ekin,0+Epot,0
Otherwise, in the presence of net work done by
non-conservative forces (e.g. friction):
Wnc = Ekin,f – Ekin,0 + Epot,f-Epot,i

7. Example ProblemExample Problem
Suppose the initial kinetic and potential energies of a system are 75J
and 250J respectively, and that the final kinetic and potential energies
of the same system are 300J and -25J respectively. How much work
was done on the system by non-conservative forces?
1. 0J
2. 50J
3. -50J
4. 225J
5. -225J
correct
Work done by non-conservative forces equals the
difference between final and initial kinetic energies
plus the difference between the final and initial
gravitational potential energies.
W = (300-75) + ((-25) - 250) = 225 - 275 = -50J.
Samar HathoutSamar Hathout

8. ExampleExample
Samar Hathout

9. Conservation of EnergyConservation of Energy
Conservative forces:
• Gravity, electrical, QCD…
Non-conservative forces:
• Friction, air resistance…
Non-conservative forces still conserve energy!
Energy just transfers to thermal energy
PEf + KEf = PEi + KEi
∆KE = −∆PE
Samar Hathout

10. ExampleExample
A diver of mass m drops from
a board 10.0 m above the
water surface, as in the
Figure. Find his speed 5.00 m
above the water surface.
Neglect air resistance.
9.9 m/s

11. ExampleExample
A skier slides down the frictionless slope as shown.
What is the skier’s speed at the bottom?
H=40 m
L=250 m
start
finish
28.0 m/s

12. ExampleExample
Three identical balls are
thrown from the top of a
building with the same initial
speed. Initially,
Ball 1 moves horizontally.
Ball 2 moves upward.
Ball 3 moves downward.
Neglecting air resistance,
which ball has the fastest
speed when it hits the ground?
A) Ball 1
B) Ball 2
C) Ball 3
D) All have the same speed.

13. Springs (Hooke’s Law)Springs (Hooke’s Law)
Proportional to
displacement
from
equilibrium
F = −kx

14. Potential Energy of SpringPotential Energy of Spring
∆PE=-F∆x
∆x
F
∆PE∑ =
1
2
(kx)x
PE =
1
2
kx2

15. x
ExampleExample
b) To what height h does the block rise when moving up
the incline?
A 0.50-kg block rests on a horizontal, frictionless
surface as in the figure; it is pressed against a light
spring having a spring constant of k = 800 N/m, with
an initial compression of 2.0 cm.
3.2 cm

16. PowerPower
Average power is the average rate at which a net force
does work:
Pav = Wnet / t
SI unit: [P] = J/s = watt (W)
Or Pav = Fnet s /t = Fnet vav

17. ExampleExample
A 1967 Corvette has a weight of 3020 lbs. The 427
cu-in engine was rated at 435 hp at 5400 rpm.
a) If the engine used all 435 hp at 100% efficiency
during acceleration, what speed would the car attain
after 6 seconds?
b) What is the average acceleration? (in “g”s)
a) 120 mph b) 0.91g

18. ExampleExample
Consider the Corvette (w=3020 lbs) having constant
acceleration of a=0.91g
a) What is the power when v=10 mph?
b) What is the power output when v=100 mph?
a) 73.1 hp b) 732 hp
(in real world a is larger at low v)