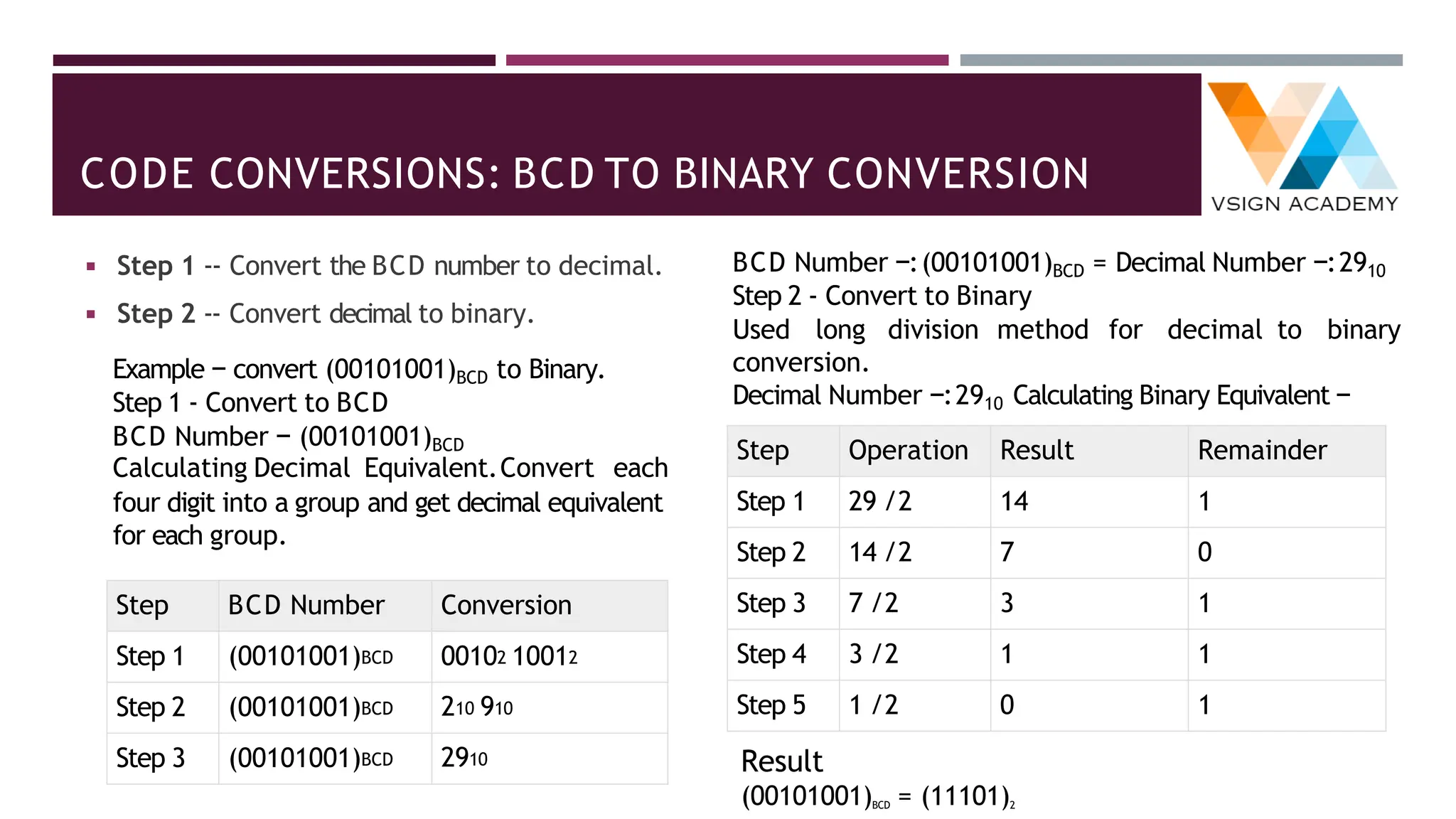
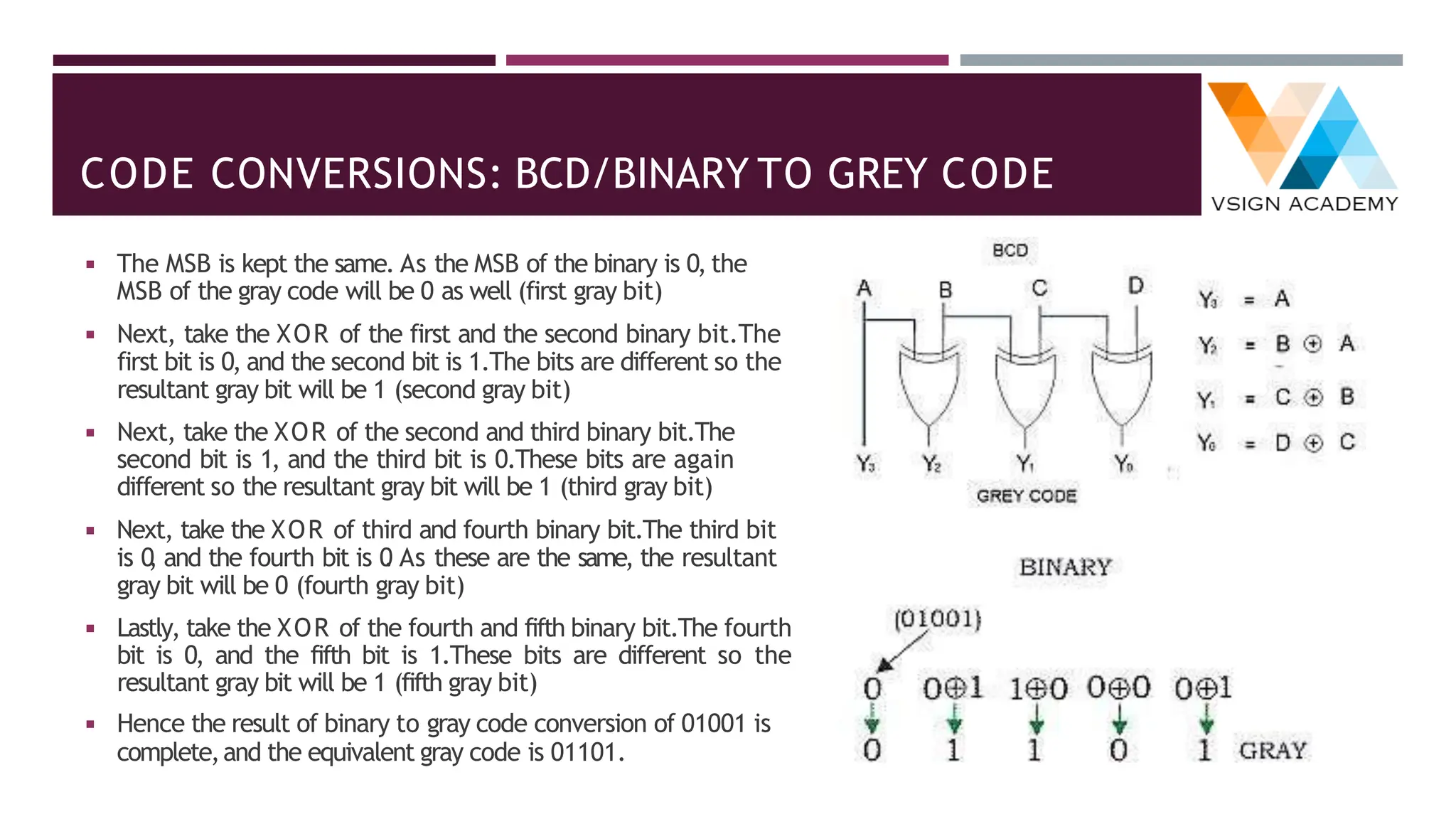
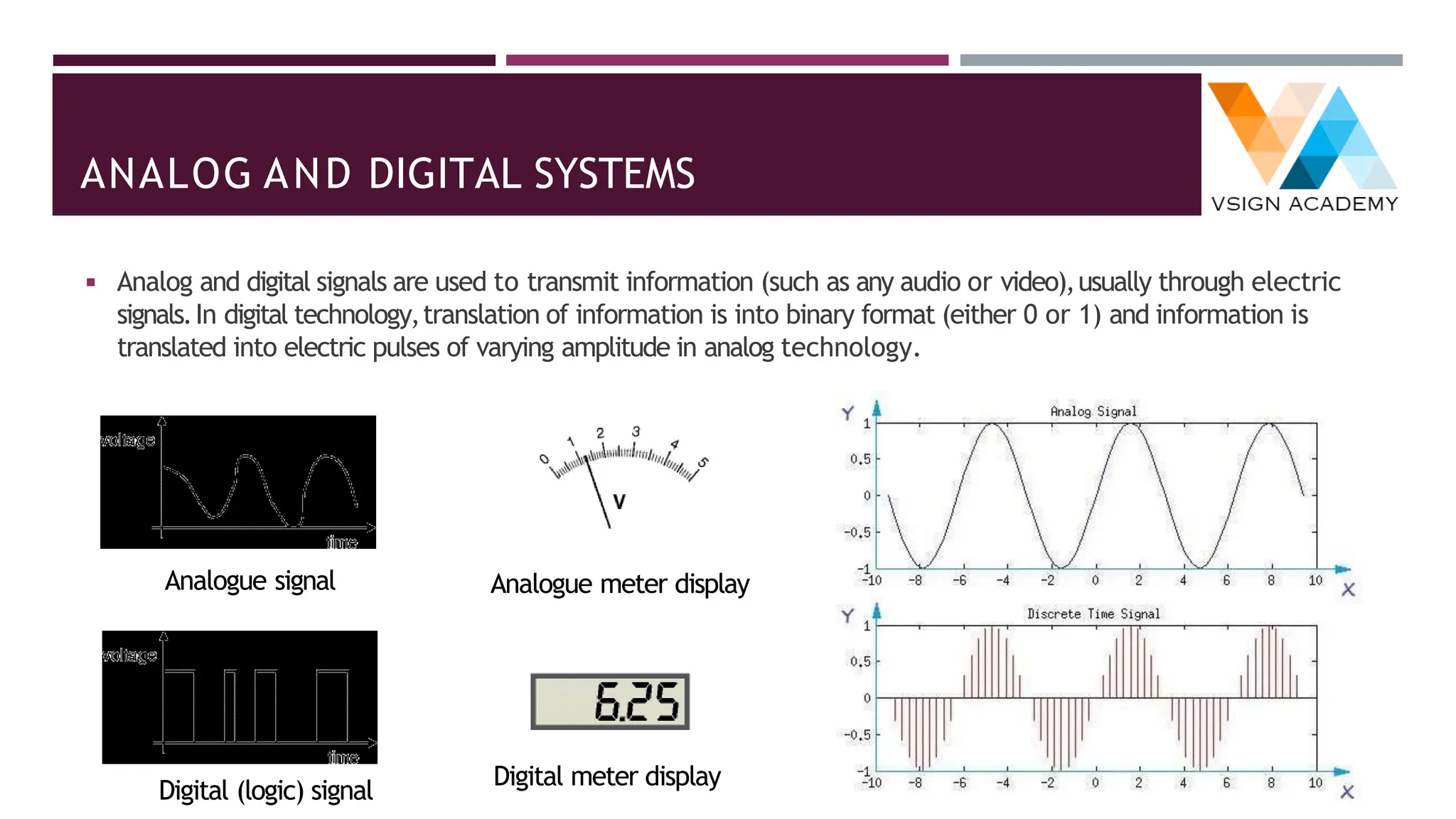
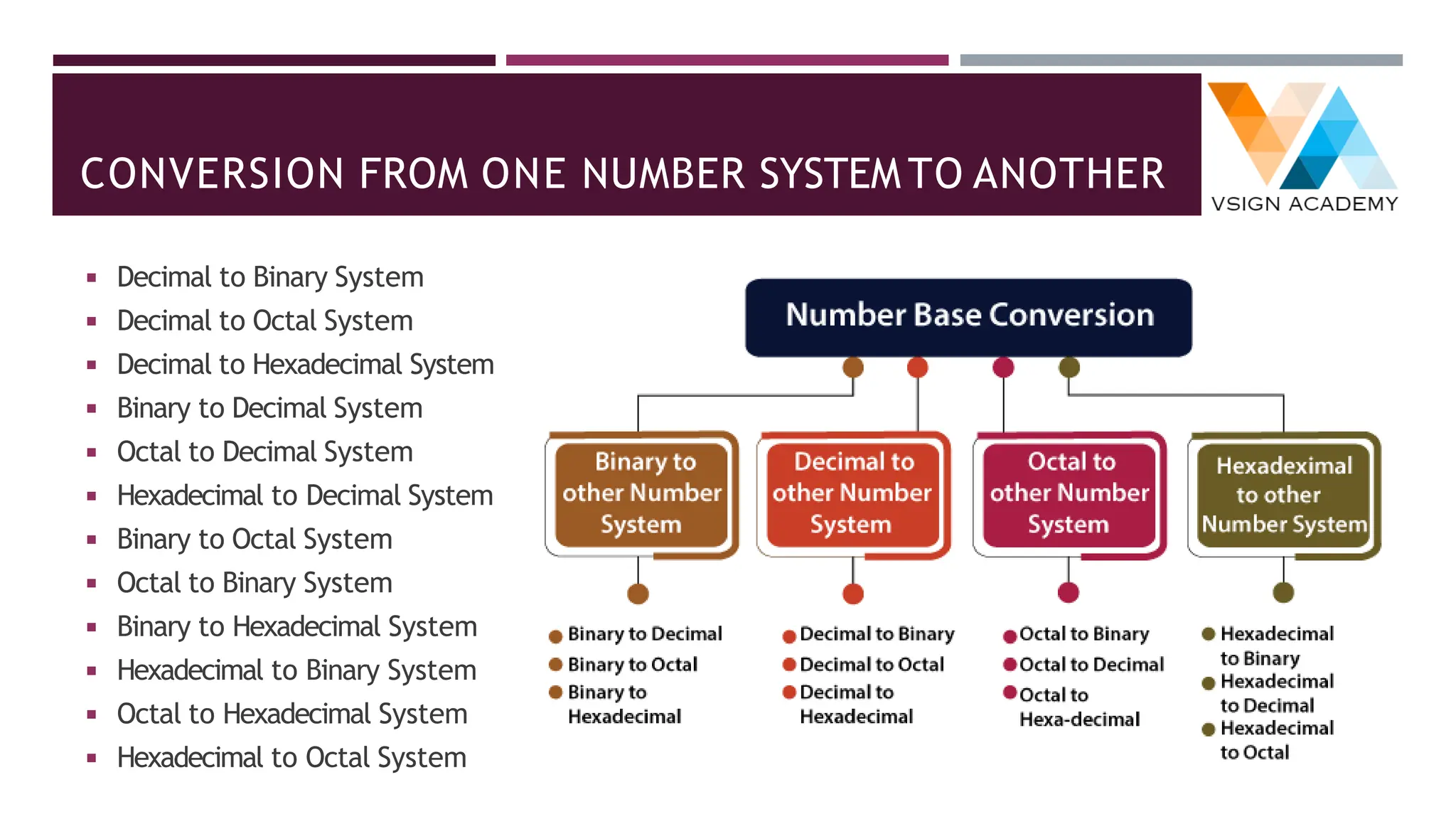
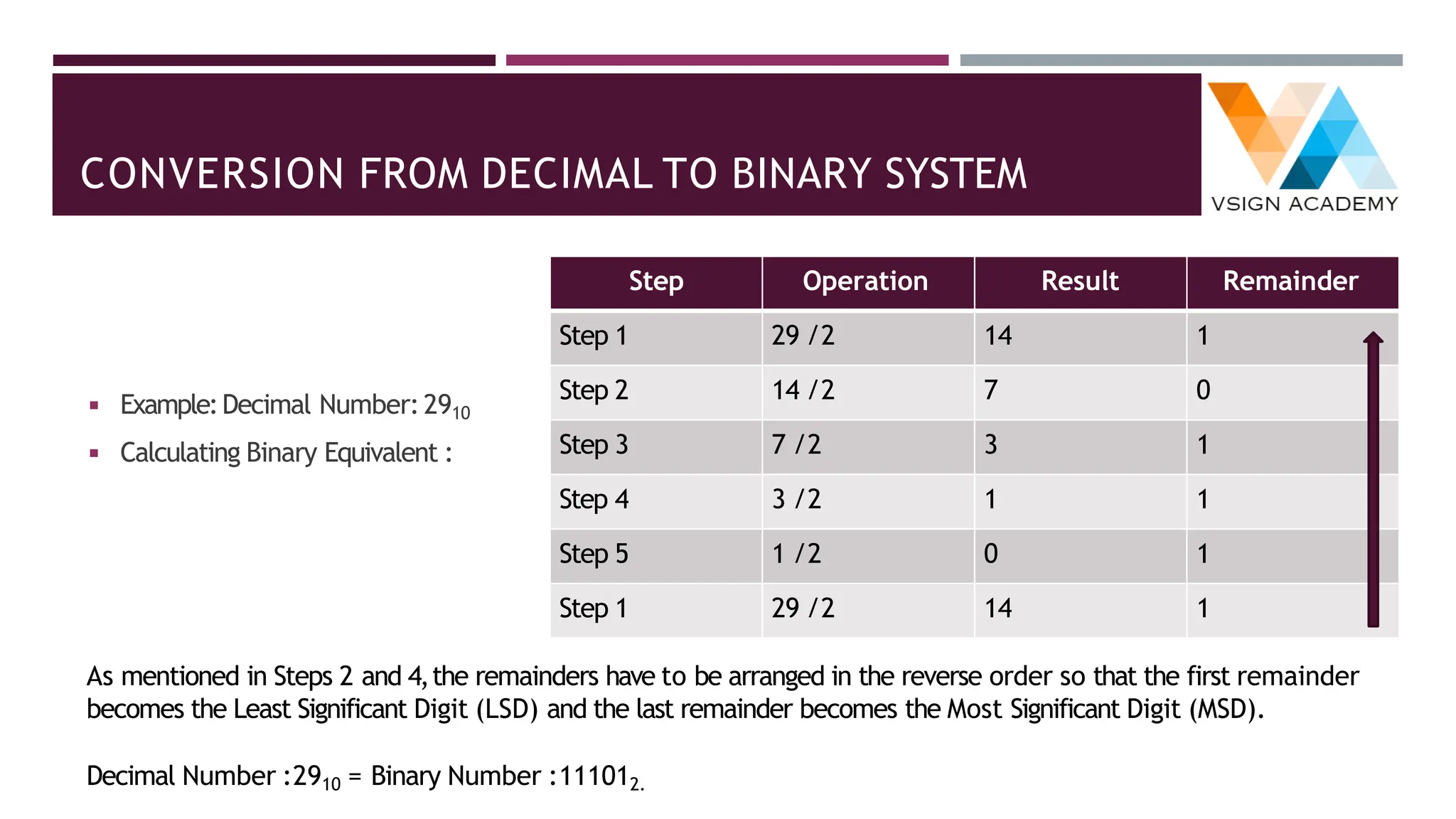
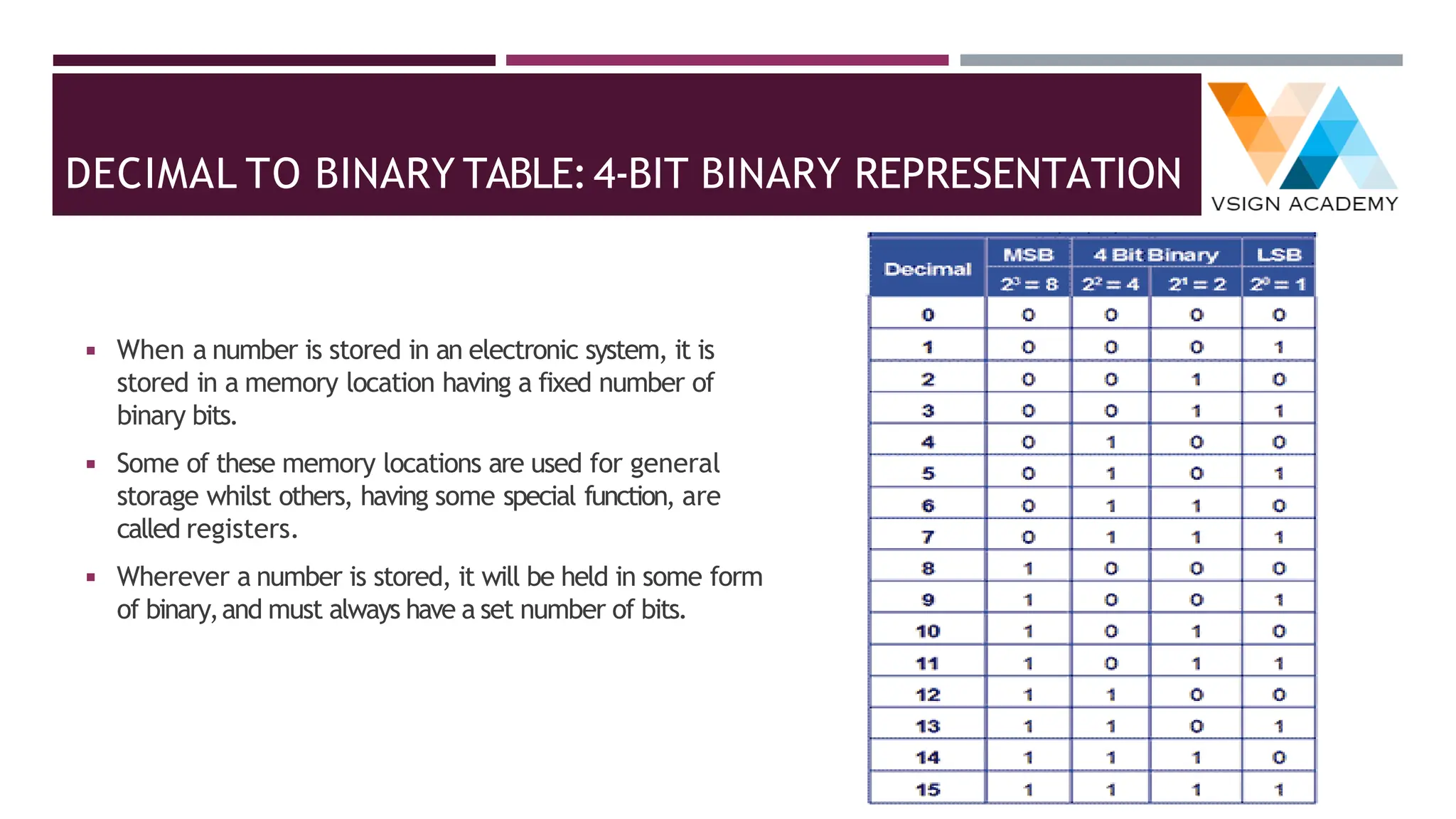
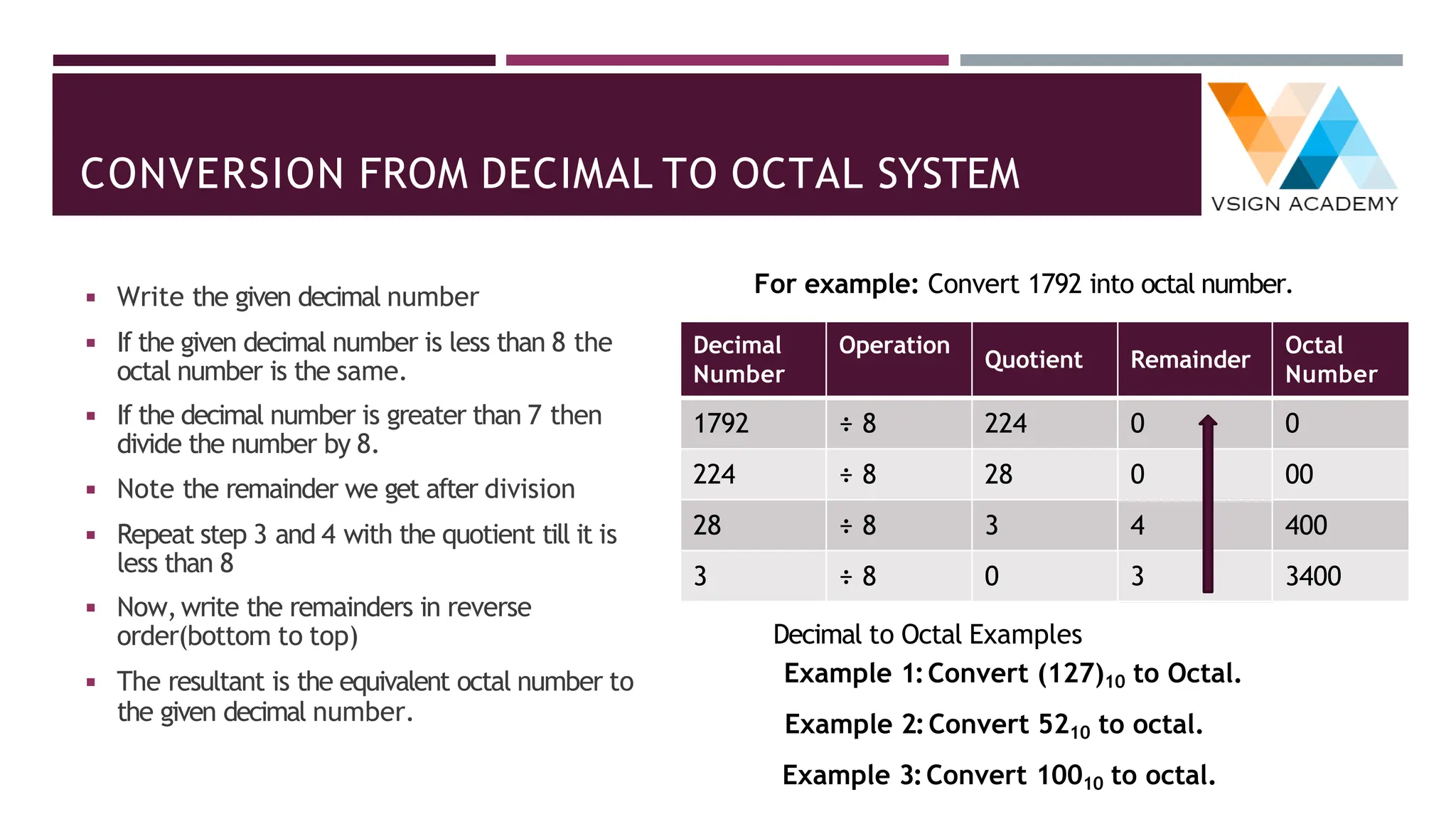
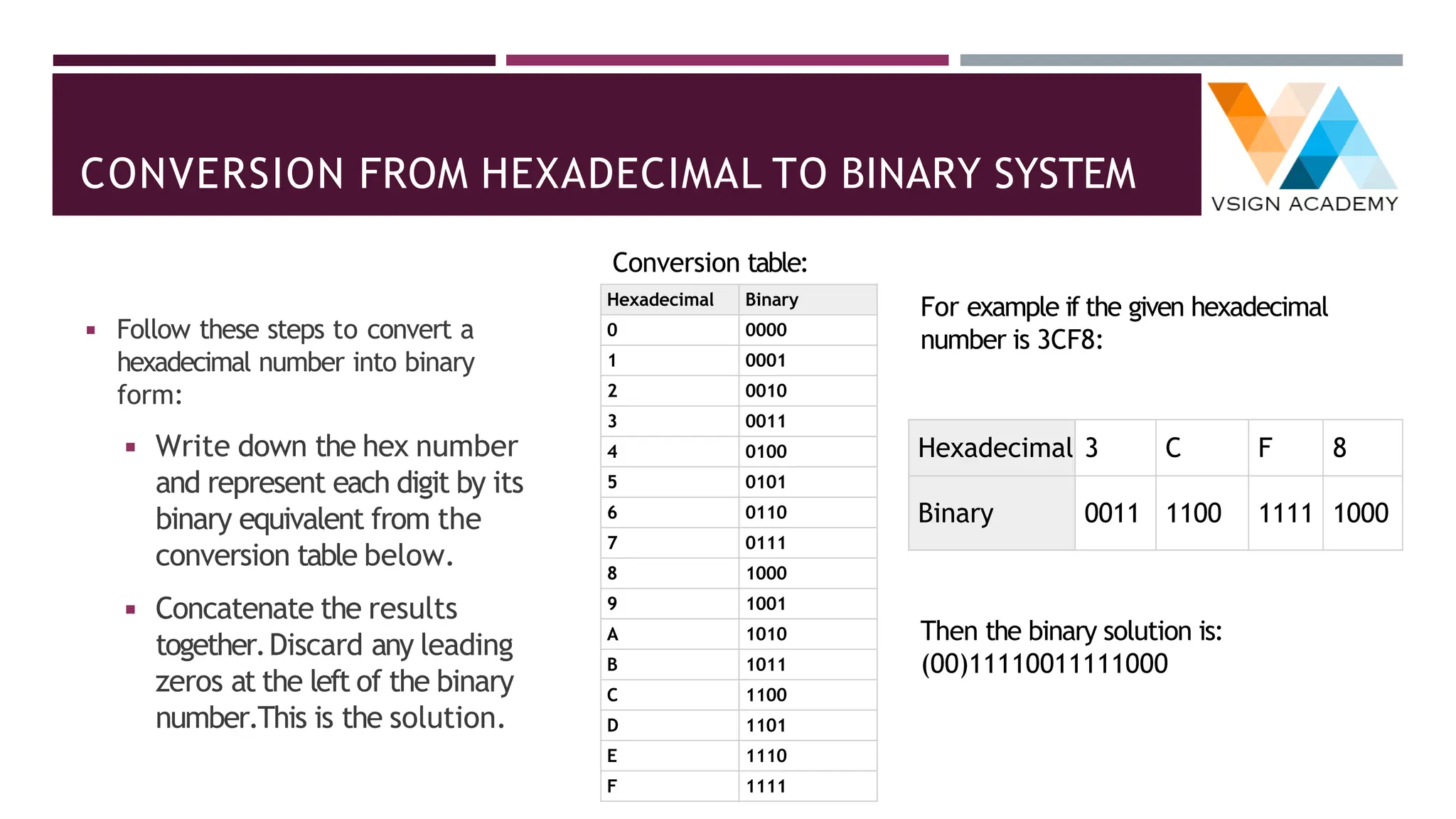
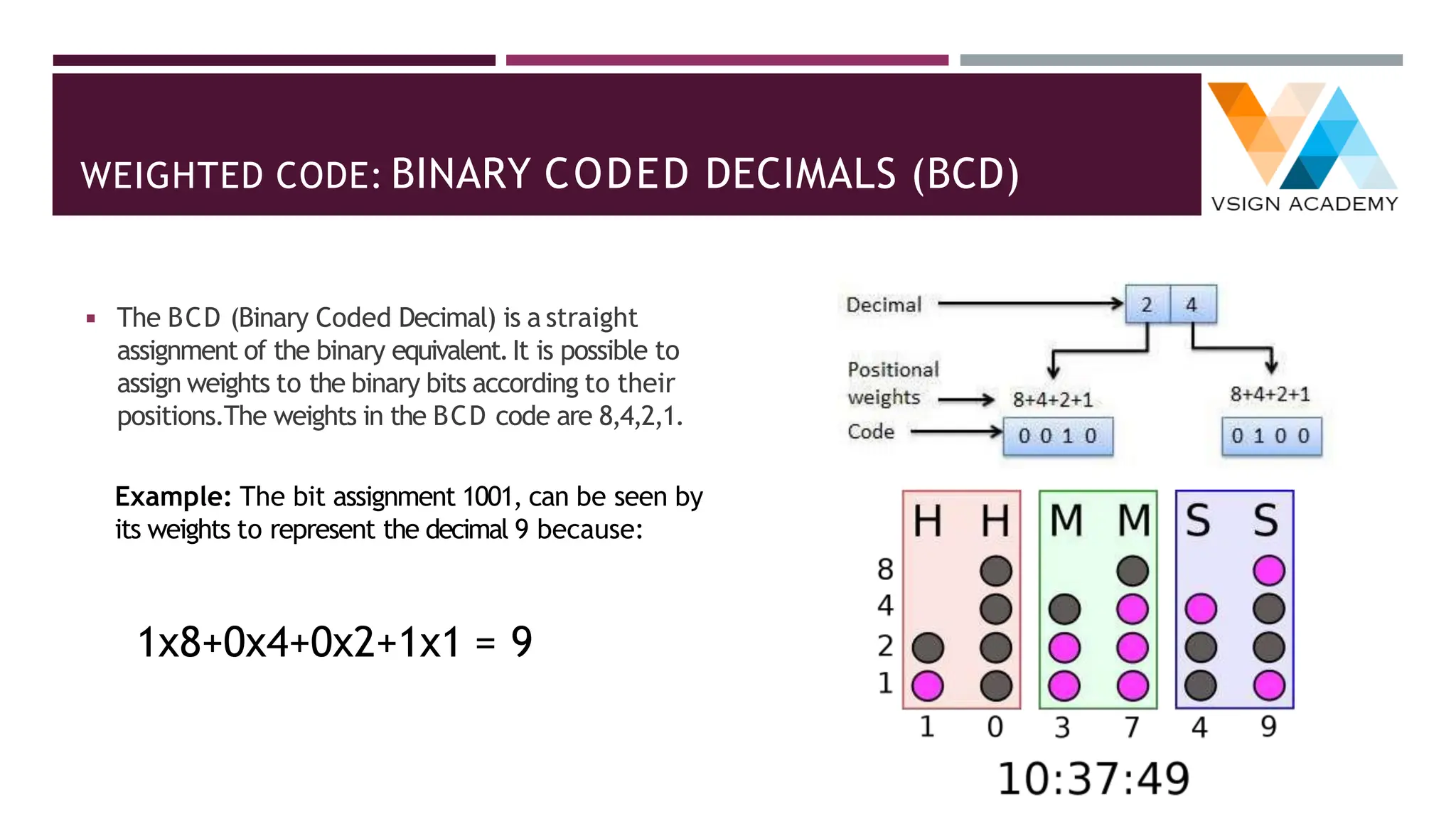
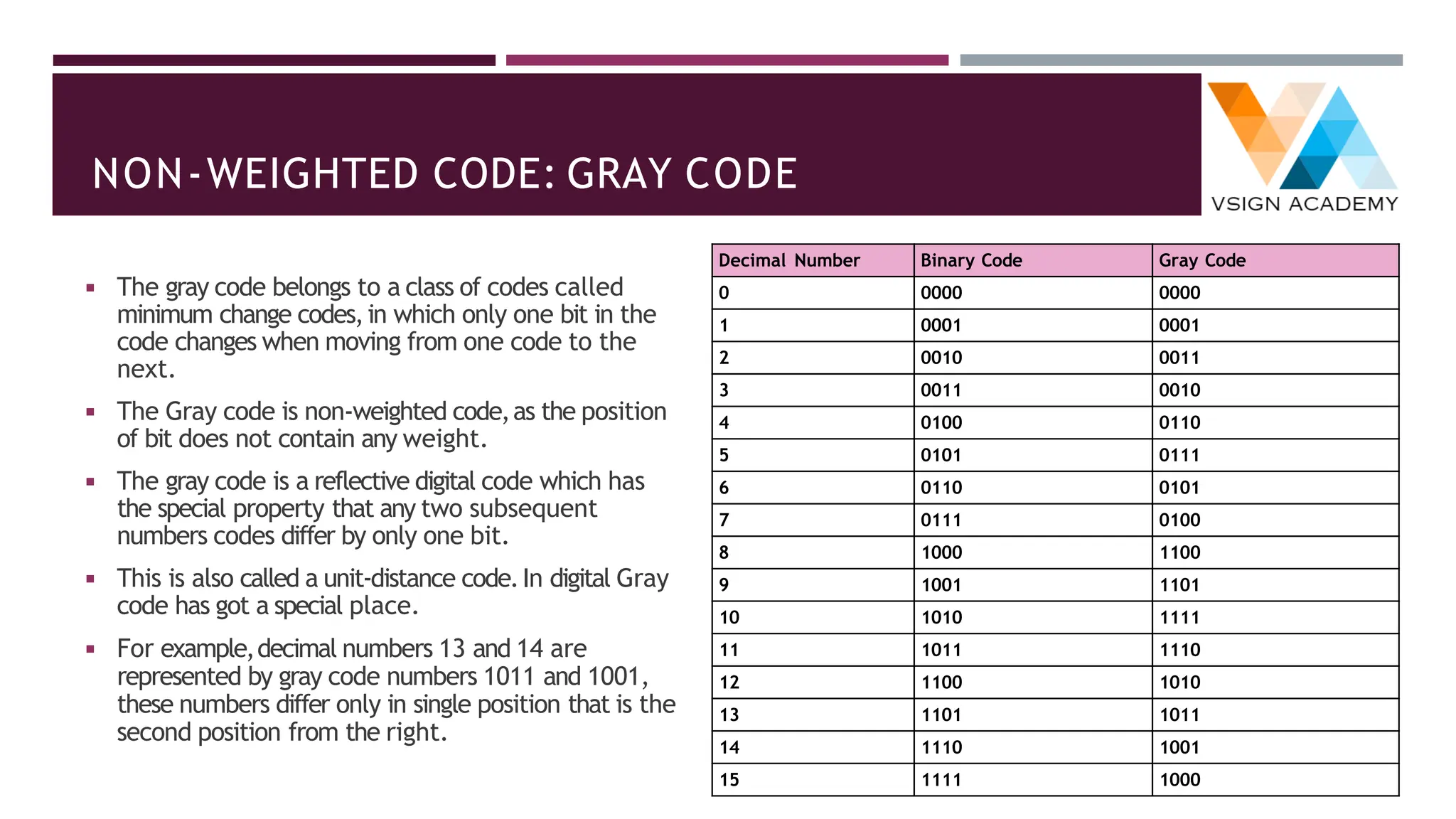
The document provides an overview of number systems including decimal, binary, octal, and hexadecimal, explaining their characteristics and conversion processes between each system. It covers binary arithmetic operations such as addition, subtraction, multiplication, and division, as well as the representation of negative numbers. Additionally, it includes methods for converting decimal and fractional numbers to and from various bases using specific algorithms.

1. NUMBER
SYSTEM
&
BINARY
ARITHMETIC
UNIT I
CHAPTER 1
DIGITAL
ELECTRONICS

2. UNIT I:CONTENTS
◾ Number System:
◾ Analog System,digital system,
◾ Numbering system,binary number system,octal number system,hexadecimal number system,conversion from one number
system to another
◾ Weighted codes binary coded decimal,non-weighted codes Excess – 3 code,Gray code,
◾ Alphanumeric codes – ASCII Code, EBCDIC, ISCII Code, Hollerith Code, Morse Code,Teletypewriter (TTY), Error
detection and correction, Universal Product Code,
◾ Code conversion.
◾ Binary Arithmetic:
◾ Binary addition,Binary subtraction,
◾ Negative number representation,
◾ Subtraction using 1’s complement and 2’s complement,Binary multiplication and division,Arithmetic in octal number system,
Arithmetic in hexadecimal number system,
◾ BCD and Excess – 3 arithmetic.
C
H
A
P
T
E
R
I
C
H
A
P
T
E
R
II

3. ANALOG AND DIGITAL SYSTEMS
◾ Analog and digital signals are used to transmit information (such as any audio or video),usually through electric
signals.In digital technology,translation of information is into binary format (either 0 or 1) and information is
translated into electric pulses of varying amplitude in analog technology.
Analogue signal Analogue meter display
Digital (logic) signal
Digital meter display

4. NUMBER SYSTEMS
◾ A computer can understand the positional
number system where there are only a few
symbols called digits and these symbols
represent different values depending on the
position they occupy in the number.
◾ The value of each digit in a number can be
determined using :
◾ The digit
◾ The position of the digit in the number
◾ The base of the number system (where the base is
defined as the total number of digits available in
the number system)

5. NUMBER SYSTEMS: DECIMAL
◾ The number system that we use in our day-to-
day life is the decimal number system.
◾ Decimal number system has base 10 as it uses
10 digits from 0 to 9.
◾ In decimal number system,the successive
positions to the left of the decimal point
represent units,tens,hundreds,thousands,and
so on.
◾ Each position represents a specific power of the
base (10).
For example,
The decimal number 1234 consists of the digit
✓4 in the units position,
✓3 in the tens position,
✓2 in the hundreds position,and
✓1 in the thousands position.
Its value can be written as
(1 x 1000)+ (2 x 100)+ (3 x 10)+ (4 x l)
➢(1 x 103)+ (2 x 102)+ (3 x 101)+ (4 x l00)
➢1000 + 200 + 30 + 4
➢1234

6. NUMBER SYSTEMS: BINARY
◾ Characteristics of the binary number system are
as follows :
◾ Uses two digits,0 and 1
◾ Also called as base 2 number system
◾ Each position in a binary number represents
a 0 power of the base (2).
◾ Example 20
◾ Last position in a binary number represents a
x power of the base (2).
◾ Example 2x where x represents the last
position - 1.
For example,
Binary Number:101012
Calculating Decimal Equivalent :
Step Binary
Number
Decimal Number
Step 1 101012 ((1 x 24) + (0 x 23) + (1 x 22) + (0 x
21) + (1 x 20))10
Step 2 101012 (16 + 0 + 4 + 0 + 1)10
Step 3 101012 2110
Note − 101012 is normally written as 10101.

7. NUMBER SYSTEMS: OCTAL
◾ Characteristics of the octal number system are
as follows :
◾ Uses eight digits,0,1,2,3,4,5,6,7
◾ Also called as base 8 number system
◾ Each position in an octal number represents a
0 power of the base (8).
◾ Example 80
◾ Last position in an octal number represents a
x power of the base (8).
◾ Example 8x where x represents the last
position - 1
For example,
Octal Number:125708
Calculating Decimal Equivalent:
Step Binary
Number
Decimal Number
Step 1 125708 ((1 x 84) + (2 x 83) + (5 x 82) + (7 x
81) + (0 x 80))10
Step 2 125708 (4096 + 1024 + 320 + 56 + 0)10
Step 3 125708 549610
Note − 125708 is normally written as 12570.

8. NUMBER SYSTEMS: HEXADECIMAL
◾ Characteristics of hexadecimal number system
are as follows:
◾ Uses 10 digits and 6 letters,0,1,2,3,4,5,6,7,8,9,
A,B,C, D,E,F
◾ Letters represent the numbers starting from 10.A
= 10.B = 11,C = 12,D = 13,E = 14,F = 15
◾ Also called as base 16 number system
◾ Each position in a hexadecimal number represents
a 0 power of the base (16).Example,160
◾ Last position in a hexadecimal number represents
a x power of the base (16).
◾ Example 16x where x represents the last position
- 1
For example,
Hexadecimal Number: 19FDE16
Calculating Decimal Equivalent:
Step Binary
Number
Decimal Number
Step 1 19FDE16 ((1 x 164) + (9 x 163) + (F x 162) +
(D x 161) + (E x 160))10
Step 2 19FDE16 ((1 x 164) + (9 x 163) + (15 x 162) +
(13 x 161) + (14 x 160))10
Step 3 19FDE16 (65536+ 36864 + 3840 + 208 +
14)10
Step 4 19FDE16 10646210
Note − 19FDE16 is normally written as 19FDE.

9. CONVERSION FROM ONE NUMBER SYSTEM TO ANOTHER
◾ Decimal to Binary System
◾ Decimal to Octal System
◾ Decimal to Hexadecimal System
◾ Binary to Decimal System
◾ Octal to Decimal System
◾ Hexadecimal to Decimal System
◾ Binary to Octal System
◾ Octal to Binary System
◾ Binary to Hexadecimal System
◾ Hexadecimal to Binary System
◾ Octal to Hexadecimal System
◾ Hexadecimal to Octal System

10. DECIMAL TO OTHER BASE SYSTEM
◾ Step 1 − Divide the decimal number to be converted by the value of the new base.
◾ Step 2 − Get the remainder from Step 1 as the rightmost digit (least significant digit) of the new base
number.
◾ Step 3 − Divide the quotient of the previous divide by the new base.
◾ Step 4 − Record the remainder from Step 3 as the next digit (to the left) of the new base number.
◾ Repeat Steps 3 and 4,getting remainders from right to left,until the quotient becomes zero in Step 3.
◾ The last remainder thus obtained will be the Most Significant Digit (MSD) of the new base number.

11. CONVERSION FROM DECIMAL TO BINARY SYSTEM
◾ Example:Decimal Number:2910
◾ Calculating Binary Equivalent :
Step Operation Result Remainder
Step 1 29 /2 14 1
Step 2 14 /2 7 0
Step 3 7 /2 3 1
Step 4 3 /2 1 1
Step 5 1 /2 0 1
Step 1 29 /2 14 1
As mentioned in Steps 2 and 4,the remainders have to be arranged in the reverse order so that the first remainder
becomes the Least Significant Digit (LSD) and the last remainder becomes the Most Significant Digit (MSD).
Decimal Number :2910 = Binary Number :111012.

12. DECIMAL TO BINARY TABLE:4-BIT BINARY REPRESENTATION
◾ When a number is stored in an electronic system, it is
stored in a memory location having a fixed number of
binary bits.
◾ Some of these memory locations are used for general
storage whilst others, having some special function, are
called registers.
◾ Wherever a number is stored, it will be held in some form
of binary,and must always have a set number of bits.

13. CONVERSION OF DECIMAL TO BINARY EXAMPLES
Conversion of Decimal to Binary method can easily be
understood by considering an example which is
explained below.
For example – Consider the conversion of the decimal
number 25 into its equivalent binary.
Divide by 2 Result Remainder Binary Value
294 ÷ 2 147 0 0 (LSB)
147 ÷ 2 73 1 1
73 ÷ 2 36 1 1
36 ÷ 2 18 0 0
18 ÷ 2 9 0 0
9 ÷ 2 4 1 1
4 ÷ 2 2 0 0
2 ÷ 2 1 0 0
1 ÷ 2 0 1 1 (MSB)
Convert the decimal number 294 into a binary number.
Therefore,the binary equivalent for the given decimal number 29410 is 1001001102

14. CONVERSION OF DECIMAL TO BINARY FOR FRACTION
NUMBER
◾ For fractional decimal numbers,multiply it by 2 and record the carry in the integral position.The carries when read
down produces the equivalent binary fraction as explained by the example given.
Thus the fractional binary number is .01011,i.e.,0.01011.
The process of multiplication by 2 will continue till the
desired accuracy is achieved.
Here is another example of such conversion using the
fraction 0.375.
Now,let’s just write out the resulting integer part at each
step — 0.011.
So,0.375 in decimal system is represented as 0.011 in
binary.
Consider the fractional binary number 0.35

15. CONVERSION OF BINARY FRACTION TO DECIMAL
NUMBER
◾ Divide each digit from right side of radix point till the end by 21,22,23,… respectively.
◾ Add all the result coming from step 1.
◾ Equivalent fractional decimal number would be the result obtained in step 2.
Step 2:Conversion of .101 to decimal
0.1012 = (1*1/2) + (0*1/22) + (1*1/23)
0.1012 = 1*0.5 + 0*0.25 + 1*0.125
0.1012 = 0.625
So equivalent decimal of binary fractional is 0.625
Number
Base
as Power
102 101 100 . 10-1 10-2 10-3
Equivalent 100 10 1 . 1/10 1/100 1/1000
Decimal Fractions
Binary Fractions
Number Base
as Power
24 23 22 21 20 . 2-1 2-2 2-3
Equivalent 16 8 4 2 1 . 1/2 1/4 1/8

16. CONVERSION FROM DECIMAL TO OCTAL SYSTEM
◾ Write the given decimal number
◾ If the given decimal number is less than 8 the
octal number is the same.
◾ If the decimal number is greater than 7 then
divide the number by 8.
◾ Note the remainder we get after division
◾ Repeat step 3 and 4 with the quotient till it is
less than 8
◾ Now,write the remainders in reverse
order(bottom to top)
◾ The resultant is the equivalent octal number to
the given decimal number.
For example: Convert 1792 into octal number.
Decimal
Number
Operation
Quotient Remainder
Octal
Number
1792 ÷ 8 224 0 0
224 ÷ 8 28 0 00
28 ÷ 8 3 4 400
3 ÷ 8 0 3 3400
Decimal to Octal Examples
Example 1:Convert (127)10 to Octal.
Example 2:Convert 5210 to octal.
Example 3:Convert 10010 to octal.

17. CONVERSION FROM DECIMAL TO OCTAL SYSTEM
◾ Example 1:Convert (127)10 to Octal.
◾ Solution: Divide 127 by 8
◾ 127 ÷ 8= 15(Quotient) and
(7)Remainder
◾ Divide 15 by 8 again.
◾ 15 ÷ 8 = 1(Quotient) and (7) Remainder
◾ Divide 1 by 8,we get;
◾ 1 ÷ 8 = 0(Quotient) and (1) Remainder
◾ Since the quotient is zero now,no more
division can be done.So by taking the
remainders in reverse order,we get the
equivalent octal number.
◾ Hence,(127)10 = (177)8
◾ Example 2: Convert 5210
to octal.
◾ Solution: Divide 52 by 8
◾ 52 ÷ 8 = 6(Quotient) and
(4)Remainder
◾ Divide 6 by 8 again.
◾ 6 ÷ 8 = 0(Quotient) and (6)
Remainder
◾ Since the quotient is zero now,
no more division can be done.
So by taking the remainders in
reverse order,we get the
equivalent octal number.
◾ Hence,(52)10 = (64)8
◾ Example 3:Convert 10010 to
octal.
◾ Solution: Divide 100 by 8
◾ 100 ÷ 8= 12(Quotient) and
(4)Remainder
◾ Divide 12 by 8 again.
◾ 12 ÷ 8 = 1(Quotient) and (4)
Remainder
◾ Divide 1 by 8,we get;
◾ 1 ÷ 8 = 0(Quotient) and (1)
Remainder
◾ Since the quotient is zero now,no
more division can be done.So by
taking the remainders in reverse
order,we get the equivalent octal
number.
◾ Hence,(100)10 = (144)8

18. CONVERSION FROM DECIMAL FRACTION TO OCTAL
SYSTEM
◾ Take decimal number as multiplicand.
◾ Multiple this number by 8 (8 is base of octal so multiplier here).
◾ Store the value of integer part of result in an array (it will be:0,1,2,3,4,5,6,and 7 because of multiplier 8).
◾ Repeat the above two steps until the number became zero
◾ Example − Convert decimal fractional number 0.140869140625 into octal number.
Multiplication Resultant integer part
0.140869140625 x 8=0.12695313 1
0.12695313 x 8=0.01562504 1
0.01562504 x 8=0.12500032 0
0.12500032 x 8=0.00000256 1
0.00000256 x 8=0.000020544 0
and so on ....
Now,write these resultant integer
part,this will be approximate 0.11010
which is equivalent octal fractional
number of decimal fractional
0.140869140625.

19. CONVERSION FROM DECIMAL TO HEXADECIMAL SYSTEM
◾ Take decimal number as dividend.
◾ Divide this number by 16 (16 is base of
hexadecimal so divisor here).
◾ Store the remainder in an array (it will be: 0
to 15 because of divisor 16,replace 10,11,
12,13,14,15 byA,B,C, D,E,F respectively).
◾ Repeat the above two steps until the
number is greater than zero.
◾ Print the array in reverse order (which will
be equivalent hexadecimal number of given
decimal number).
Example − Convert decimal number 540 into hexadecimal
number.
Division Remainder (R)
540 /16 = 33 12 = C
33 /16 = 2 1
2 /16 = 0 2
0 /16 = 0 0

20. CONVERSION FROM DECIMAL FRACTION TO
HEXADECIMAL
◾ Take decimal number as multiplicand.
◾ Multiple this number by 16 (16 is base of
hexadecimal so multiplier here).
◾ Store the value of integer part of result in an
array (it will be:0 to 15,because of
multiplier 16,replace 10,11,12,13,14,15 by
A,B,C, D,E,F respectively).
◾ Repeat the above two steps until the
number became zero.
◾ Print the array (which will be equivalent
fractional hexadecimal number of given
decimal fractional number).
Example − Convert decimal fractional number 0.06640625
into hexadecimal number.
Multiplication Resultant integer part
0.06640625 x 16=1.0625 1
0.0625 x 16 =1.0 1
0 x 16=0.0 0

21. CONVERSION FROM BINARY TO DECIMAL SYSTEM
◾ Converting from binary to decimal involves multiplying
the value of each digit (i.e.1 or 0) by the value of the
placeholder in the number
◾ Write down the number.
◾ Starting with the LSB,multiply the digit by the value
of the place holder.
◾ Continue doing this until you reach the MSB.
◾ Add the results together.
Placeholder Value in the Decimal Numbering System Most Significant Bit (MSB) and Least Significant Bit (LSB)
Placeholder Value in the Binary Numbering System

22. STEPSTO CONVERT BINARY TO DECIMAL
For example,
Binary Number:101012
Calculating Decimal Equivalent :
Step Binary
Number
Decimal Number
Step 1 101012 ((1 x 24) + (0 x 23) + (1 x 22) + (0 x
21) + (1 x 20))10
Step 2 101012 (16 + 0 + 4 + 0 + 1)10
Step 3 101012 2110

23. CONVERSION FROM OCTAL TO DECIMAL SYSTEM
◾ Converting octal to decimal can be done as
following:
◾ Write the powers of 8 (1,8,64,512,4096,and
so on) beside the octal digits from bottom to
top.
◾ Multiply each digit by it's power.
◾ Add up the answers.This is the solution.
For example if the given octal number is 50173:
Digit Power Multiplication
5 4096 20480
0 512 0
1 64 64
7 8 56
3 1 3
Then the decimal solution (20480 + 64 + 56 + 3) is: 20603
✓ The octal numeral system,or oct for short,is the base-8 number system,and uses the digits 0 to 7.
✓ It has the advantage of not requiring any extra symbols as digits.
✓ It is also used for digital displays.

24. CONVERSION FROM HEXADECIMAL TO DECIMAL SYSTEM
◾ Follow these steps to convert a hexadecimal number into
decimal form:
◾ Write the powers of 16 (1,16,256,4096,65536,and
so on) beside the hex digits from bottom to top.
◾ Convert any letters (A to F) to their corresponding
numerical form.
◾ Multiply each digit by it's power.
◾ Add up the answers.This is the solution.
For example if the given hexadecimal
number is 6FC7:
Digit Power Multiplication
6 4096 24576
F (15) 256 3840
C (12) 16 192
7 1 7
Then the decimal solution (24576 + 3840 +
192 + 7) is: 28615
✓ Hexadecimal is a positional system that represents numbers using a base of 16.
✓ Unlike the common way of representing numbers with ten symbols,it uses sixteen distinct symbols,most often the
symbols "0"-"9" to represent values zero to nine,and "A"-"F" to represent values ten to fifteen.
✓ Hexadecimal numerals are widely used by computer system designers and programmers,as they provide a human-
friendly representation of binary-coded values.

25. CONVERSION FROM BINARY TO OCTAL SYSTEM
◾ Follow these steps to convert a binary
number into octal form:
◾ Start from the right side of the
binary number and divide it up into
groups of 3 digits.Add extra zeros
to the front of the first number if it
is not three digits.
◾ Convert each group of 3 binary
digits to its equivalent octal value
from the conversion table below.
◾ Concatenate the results together.
This is the solution.
Conversion table:
Binary Octal
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
For example if the given binary number is
10110111010001:
Binary (0)10 110 111 010 001
Octal 2 6 7 2 1
Then the octal solution is:26721

26. CONVERSION FROM OCTAL TO BINARY SYSTEM
◾ Follow these steps to convert a
octal number into binary form:
◾ Write down the octal number
and represent each digit by its
binary equivalent from the
conversion table below.
◾ Concatenate the results
together.Discard any leading
zeros at the left of the binary
number.This is the solution.
Conversion table:
Octal Binary
0 000
1 001
2 010
3 011
4 100
5 101
6 110
7 111
For example if the given octal number is 21073:
Octal 2 1 0 7 3
Binary 010 001 000 111 011
Then the binary solution is:(0)10001000111011

27. CONVERSION FROM BINARY TO HEXADECIMAL SYSTEM
◾ Follow these steps to convert a
binary number into hexadecimal
form:
◾ Start from the right side of the binary
number and divide it up into groups of
4 digits.Add extra zeros to the front
of the first number if it is not four
digits.
◾ Convert each group of 4 binary digits
to its equivalent hex value from the
conversion table below.
◾ Concatenate the results together.This
is the solution.
Conversion table:
Binary Hexadecimal
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F
For example if the given binary
number is 11011010100111:
Binary (00)11 0110 1010 0111
Hexad
ecimal
3 6 A 7
Then the hexadecimal solution is:
36A7

28. CONVERSION FROM HEXADECIMAL TO BINARY SYSTEM
◾ Follow these steps to convert a
hexadecimal number into binary
form:
◾ Write down the hex number
and represent each digit by its
binary equivalent from the
conversion table below.
◾ Concatenate the results
together.Discard any leading
zeros at the left of the binary
number.This is the solution.
Conversion table:
Hexadecimal Binary
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
A 1010
B 1011
C 1100
D 1101
E 1110
F 1111
For example if the given hexadecimal
number is 3CF8:
Hexadecimal 3 C F 8
Binary 0011 1100 1111 1000
Then the binary solution is:
(00)11110011111000

29. CONVERSION FROM OCTAL TO HEXADECIMAL SYSTEM
◾ While converting from octal to
hexadecimal unit,it is a usual practice
to convert the octal to hexadecimal by
converting the octal number into
binary digit and then further to from
binary to hexadecimal.
For example to convert the number 536 from
octal to hexadecimal.
Convert 536(octal) into its binary equivalent we get
(536)8 = (101) (011) (110)
=(101011110)2
Now forming the group of 4 binary bits to obtain its hexadecimal
equivalent,
(101011110)2= (0001) (0101) (1110)
= (15E)16
So the hexadecimal number of 536 is 15E.

30. CONVERSION FROM HEXADECIMAL TO OCTAL SYSTEM
◾ Method to Convert Hex to Octal
◾ For each given hexadecimal number digit,
write the equivalent binary number.If any
of the binary equivalents are less than 4
digits,add 0’s to the left side.
◾ Combine and make the groups of binary
digits from right to left,each containing 3
digits.Add 0’s to the left if there are less
than 3 digits in the last group.
◾ Find the octal equivalent of each binary
group.
Example: Convert 1BC16 into an octal number.
Solution:
Given,1BC16 is a hexadecimal number.
1 → 0001,B → 1011,C →1100
Now group them from right to left,each having 3 digits.
000,110,111,100
000→0, 110 →6,111→7, 100→4
Hence,1BC16 = 6748

31. EXERCISES (NUMBER SYSTEMS CONVERSION)
1.Convert the following decimal numbers into binary and hexadecimal
numbers:
1.108
2.4848
3.9000
2.Convert the following binary numbers into hexadecimal and decimal
numbers:
1.1000011000
2.10000000
3.101010101010
3.Convert the following hexadecimal numbers into binary and decimal
numbers:
1.ABCDE
2.1234
3. 80F
4.Convert the following decimal numbers into binary equivalent:
1.19.25D
2.123.456D
1.1101100B, 1001011110000B, 10001100101000B, 6CH,
12F0H, 2328H.
2.218H, 80H, AAAH, 536D, 128D, 2730D.
3.10101011110011011110B, 1001000110100B,
100000001111B, 703710D, 4660D, 2063D.
4.?? (You work it out!)

32. WEIGHTED & NON-WEIGHTED CODES
◾ Weighted Codes: The weighted codes are those that
obey the position weighting principle,which states that the
position of each number represent a specific weight.In
these codes each decimal digit is represented by a group of
four bits.
◾ In weighted codes,each digit is assigned a specific weight
according to its position.For example,in 8421/BCD code,
1001 the weights of 1,1,0,1 (from left to right) are 8,4,2
and 1 respectively.
◾ Non-weighted codes: The non-weighted codes are not
positionally weighted . In other words codes that are not
assigned with any weight to each digit position.

33. WEIGHTED CODE: BINARY CODED DECIMALS (BCD)
◾ The BCD (Binary Coded Decimal) is a straight
assignment of the binary equivalent.It is possible to
assign weights to the binary bits according to their
positions.The weights in the BCD code are 8,4,2,1.
Example: The bit assignment 1001, can be seen by
its weights to represent the decimal 9 because:
1x8+0x4+0x2+1x1 = 9

34. BINARY CODED DECIMALS (BCD)
Conversion from Decimal to BCD Conversion from BCD to Decimal

35. NON-WEIGHTED CODE: EXCESS – 3 CODE
◾ Excess-3 is a non weighted code used to express decimal numbers.The code derives its name from
the fact that each binary code is the corresponding 8421 code plus 0011(3).
◾ An Excess-3 equivalent of a given binary binary number is obtained using the following steps:
◾ Find the decimal equivalent of the given binary number.
◾ Add +3 to each digit of decimal number.
◾ Convert the newly obtained decimal number back to binary number to get required excess-3 equivalent.
◾ You can add 0011 to each four-bit group in binary coded decimal number (BCD) to get desired
excess-3 equivalent.
Example: 1000 of 8421 = 1011 in Excess-3

36. NON-WEIGHTED CODE: EXCESS – 3 CODE
◾ These are following excess-3 codes for decimal digits:
Decimal Digit BCD Code Excess-3 Code
0 0000 0011
1 0001 0100
2 0010 0101
3 0011 0110
4 0100 0111
5 0101 1000
6 0110 1001
7 0111 1010
8 1000 1011
9 1001 1100

37. NON-WEIGHTED CODE: EXCESS – 3 CODE
◾ Example-1:Convert decimal number 23 to
Excess-3 code.
◾ So,according to excess-3 code we need to add 3
to both digit in the decimal number then
convert into 4-bit binary number for result of
each digit.Therefore,
= 23+33=56 =0101 0110 which is required
excess-3 code for given decimal number 23.
◾ Example-2:Convert decimal number 15.46 into
Excess-3 code.
◾ According to excess-3 code we need to add 3 to
both digit in the decimal number then convert into
4-bit binary number for result of each digit.
Therefore,
= 15.46+33.33=48.79 =0100 1000.0111 1001 which
is required excess-3 code for given decimal number
15.46.

38. XS-3 CONVERTING INTO BINARY CODED DECIMAL (BCD)
CODES
◾ One should note that to given Excess-3 code,the equivalent decimal number can be determined by splitting
number into 4-bit group starting from least significant for integer part and from leftmost digit for fractional part.
Then subtract 0011 (=3) from each four-bit group that will be binary decimal digit (BCD) form of that number.
Now you can also convert this BCD code into decimal number by converting each 4-bit group into decimal digit.
◾ Example: Convert Excess-3 code 1001001 into BCD and decimal number.
◾ So,grouping 4-bit for each group,i.e.,0100 1001 and subtract 0011 0011 from given number.
Therefore,
= 0100 1001 -0011 0011 =0001 0110
◾ So,binary coded decimal number is 0001 0110 and decimal number will be 16.

39. NON-WEIGHTED CODE: GRAY CODE
◾ The gray code belongs to a class of codes called
minimum change codes,in which only one bit in the
code changes when moving from one code to the
next.
◾ The Gray code is non-weighted code,as the position
of bit does not contain any weight.
◾ The gray code is a reflective digital code which has
the special property that any two subsequent
numbers codes differ by only one bit.
◾ This is also called a unit-distance code.In digital Gray
code has got a special place.
◾ For example,decimal numbers 13 and 14 are
represented by gray code numbers 1011 and 1001,
these numbers differ only in single position that is the
second position from the right.
Decimal Number Binary Code Gray Code
0 0000 0000
1 0001 0001
2 0010 0011
3 0011 0010
4 0100 0110
5 0101 0111
6 0110 0101
7 0111 0100
8 1000 1100
9 1001 1101
10 1010 1111
11 1011 1110
12 1100 1010
13 1101 1011
14 1110 1001
15 1111 1000

40. ALPHANUMERIC CODES
◾ The alphanumeric codes are the codes that represent numbers and alphabetic characters.
◾ An alphanumeric code should at least represent 10 digits and 26 letters of alphabet i.e.total 36 items.
◾ Alphanumeric codes are sometimes called character codes due to their certain properties.
◾ These codes are basically binary codes.
◾ We can write alphanumeric data,including data,letters of the alphabet,numbers,mathematical symbols and
punctuation marks by this code which can be easily understandable and can be processed by the computers.
◾ ASCII Code
◾ EBCDIC

41. ASCII CODE
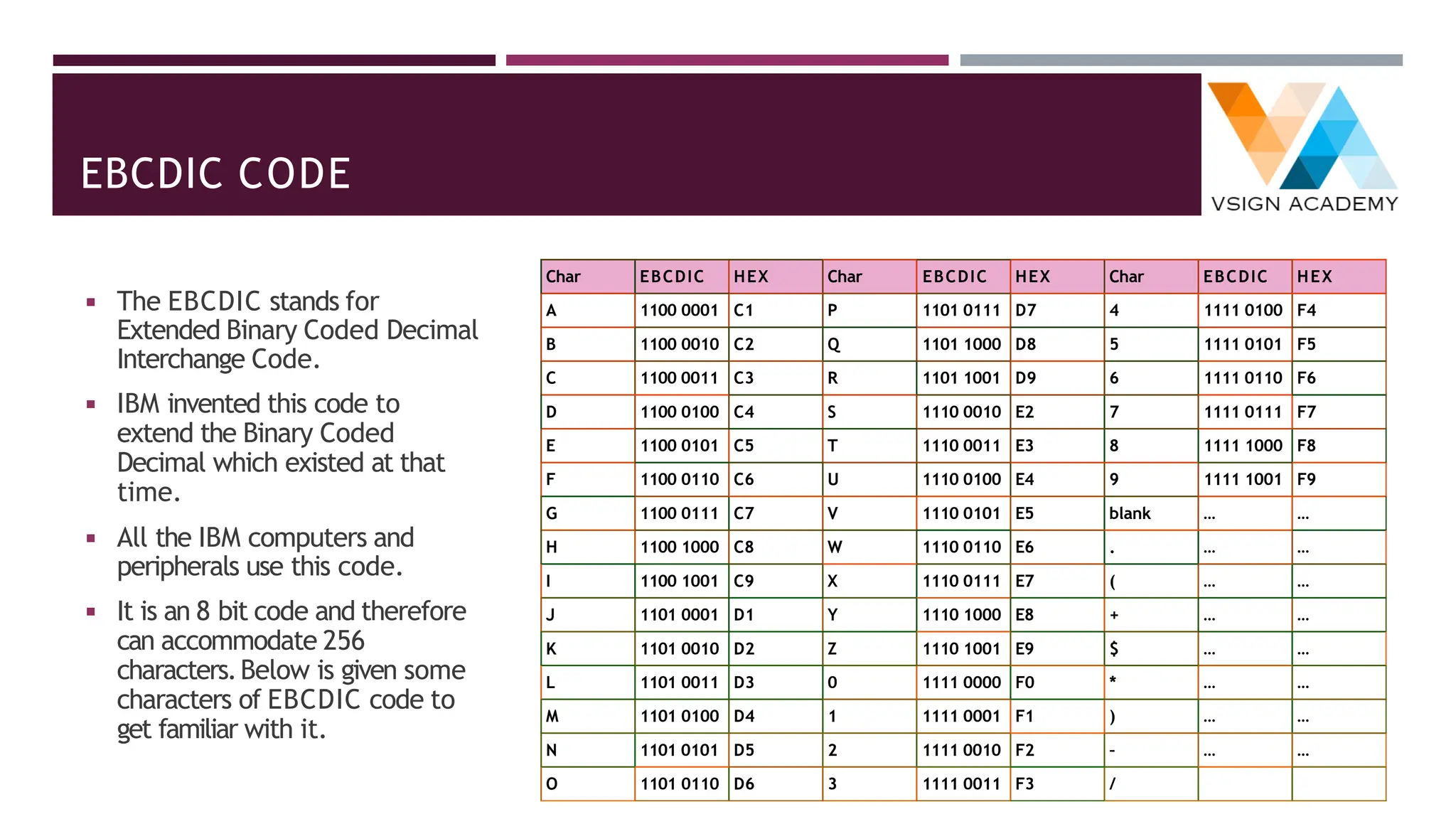
◾ The full form ofASCII code isAmerican Standard Code for Information Interchange.
◾ ASCII is originally a 7-bit code.It has been extended to 8-bit to better utilize the 8-bit computer memory organization.
◾ In 1967 this code was first published and since then it is being modified and updated.ASCII code has 128 characters some
of which are enlisted below to get familiar with the code.
Hex 0 1 2 3 4 5 6 7 8 9 A B C D E F
2 SP ! " # $ % & ' ( ) * + , - . /
3 0 1 2 3 4 5 6 7 8 9 : ; < = > ?
4 @ A B C D E F G H I J K L M N O
5 P Q R S T U V W X Y Z [ ] ^ _
6 ` a b c d e f g h i j k l m n o
7 p q r s t u v w x y z { | } ~

42. EBCDIC CODE
◾ The EBCDIC stands for
Extended Binary Coded Decimal
Interchange Code.
◾ IBM invented this code to
extend the Binary Coded
Decimal which existed at that
time.
◾ All the IBM computers and
peripherals use this code.
◾ It is an 8 bit code and therefore
can accommodate 256
characters.Below is given some
characters of EBCDIC code to
get familiar with it.
Char EBCDIC HEX Char EBCDIC HEX Char EBCDIC HEX
A 1100 0001 C1 P 1101 0111 D7 4 1111 0100 F4
B 1100 0010 C2 Q 1101 1000 D8 5 1111 0101 F5
C 1100 0011 C3 R 1101 1001 D9 6 1111 0110 F6
D 1100 0100 C4 S 1110 0010 E2 7 1111 0111 F7
E 1100 0101 C5 T 1110 0011 E3 8 1111 1000 F8
F 1100 0110 C6 U 1110 0100 E4 9 1111 1001 F9
G 1100 0111 C7 V 1110 0101 E5 blank … …
H 1100 1000 C8 W 1110 0110 E6 . … …
I 1100 1001 C9 X 1110 0111 E7 ( … …
J 1101 0001 D1 Y 1110 1000 E8 + … …
K 1101 0010 D2 Z 1110 1001 E9 $ … …
L 1101 0011 D3 0 1111 0000 F0 * … …
M 1101 0100 D4 1 1111 0001 F1 ) … …
N 1101 0101 D5 2 1111 0010 F2 – … …
O 1101 0110 D6 3 1111 0011 F3 /

43. CODE CONVERSIONS
◾ There are many methods or techniques which can be used to convert code from one
format to another as following:
◾ Binary to BCD Conversion
◾ BCD to Binary Conversion
◾ BCD to Excess-3
◾ Excess-3 to BCD
◾ BCD/Binary to Gray
◾ Gray to Binary

44. CODE CONVERSIONS: BINARY TO BCD CONVERSION
◾ Step 1 -- Convert the binary number to decimal.
◾ Step 2 -- Convert decimal number to BCD.
Example − convert (11101)2 to BCD.
Step 1 − Convert to Decimal
Binary Number −:111012
Calculating Decimal Equivalent −:
Step Binary
Number
Decimal Number
Step 1 111012 ((1 × 2
4
) + (1 × 2
3
) + (1 × 2
2
) +
(0 × 2
1
) + (1 × 2
0
))10
Step 2 111012 (16 + 8 + 4 + 0 + 1)10
Step 3 111012 2910
Binary Number −:111012 = Decimal Number −:2910
Step 2 − Convert to BCD
Decimal Number −:2910
Calculating BCD Equivalent. Convert each digit into
groups of four binary digits equivalent.
Step Decimal Number Conversion
Step 1 2910 00102 10012
Step 2 2910 00101001BCD
Result
(11101)2 = (00101001)BCD

45. CODE CONVERSIONS: BCD TO BINARY CONVERSION
◾ Step 1 -- Convert the BCD number to decimal.
◾ Step 2 -- Convert decimal to binary.
Example − convert (00101001)BCD to Binary.
Step 1 - Convert to BCD
BCD Number − (00101001)BCD
Calculating Decimal Equivalent.Convert each
four digit into a group and get decimal equivalent
for each group.
Step BCD Number Conversion
Step 1 (00101001)BCD 00102 10012
Step 2 (00101001)BCD 210 910
Step 3 (00101001)BCD 2910
BCD Number −:(00101001)BCD = Decimal Number −:2910
Step 2 - Convert to Binary
Used long division method for decimal to binary
conversion.
Decimal Number −:2910 Calculating Binary Equivalent −
Step Operation Result Remainder
Step 1 29 /2 14 1
Step 2 14 /2 7 0
Step 3 7 /2 3 1
Step 4 3 /2 1 1
Step 5 1 /2 0 1
Result
(00101001)BCD = (11101)2

46. CODE CONVERSIONS: BCD TO EXCESS-3 & EXCESS-3TO BCD
CONVERSION
◾ Step 1 -- Convert BCD to decimal.
◾ Step 2 --Add (3)10 to this decimal number.
◾ Step 3 -- Convert into binary to get excess-3 code.
Example − convert (0110)BCD to Excess-3.
Step 1 − Convert to decimal
(0110)BCD = 610
Step 2 − Add 3 to decimal
(6) + (3) = (9)
10 10 10
Step 3 − Convert to Excess-3
(9)10 = (1001)2
(0110)BCD = (1001)XS-3
Result
Subtract (0011)2
BCD
◾ Step 1 -- Subtract (0011)2 from each 4 bit of excess-3
digit to obtain the corresponding BCD code.
Example − convert (10011010)XS-3 to BCD.
Given XS-3 number = 1 0 0 1 1 0 1 0
= 1 0 0 1 0 1 1 1
--------------------
= 0 1 1 0 0 1 1 1
(10011010)XS-3 = (01100111)BCD
Result

47. CODE CONVERSIONS: BCD/BINARY TO GREY CODE
◾ The MSB is kept the same. As the MSB of the binary is 0, the
MSB of the gray code will be 0 as well (first gray bit)
◾ Next, take the XOR of the first and the second binary bit.The
first bit is 0, and the second bit is 1.The bits are different so the
resultant gray bit will be 1 (second gray bit)
◾ Next, take the XOR of the second and third binary bit.The
second bit is 1, and the third bit is 0.These bits are again
different so the resultant gray bit will be 1 (third gray bit)
◾ Next, take the XOR of third and fourth binary bit.The third bit
is 0
, and the fourth bit is 0
. As these are the same, the resultant
gray bit will be 0 (fourth gray bit)
◾ Lastly, take the XOR of the fourth and fifth binary bit.The fourth
bit is 0, and the fifth bit is 1.These bits are different so the
resultant gray bit will be 1 (fifth gray bit)
◾ Hence the result of binary to gray code conversion of 01001 is
complete,and the equivalent gray code is 01101.

48. CODE CONVERSIONS: GRAY CODE TO BINARY
CONVERSION
◾ The MSB of the binary number will be equal to the MSB of the given gray code.
◾ Now if the second gray bit is 0,then the second binary bit will be the same as the previous or the first bit.If the
gray bit is 1 the second binary bit will alter.If it was 1 it will be 0 and if it was 0 it will be 1.
◾ This step is continued for all the bits to do Gray code to binary conversion.

49. THANK YOU!