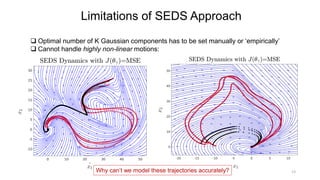
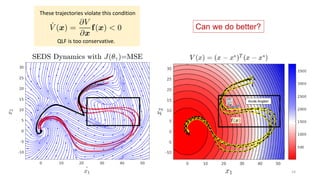
The document discusses different methods for learning dynamical systems from demonstrations, including using Gaussian mixture models with stability constraints, linear parameter varying dynamical systems, and extensions that use more complex Lyapunov functions. It compares the performance of these approaches and outlines their limitations, such as sensitivity to the number of Gaussian components and quality of the mixture model fit. A number of referenced publications are also listed that are relevant to dynamical system learning from demonstrations.

1. Learning Dynamical Systems
from Demonstrations
0
Organizers/Speakers: Nadia Figueroa, Sina Mirrazavi, Lukas Huber,
Aude Billard

2. Representing Robot Motions with an
Autonomous Dynamical System (DS)
Velocity Position Target
Variables
1

3. Representing Robot Motions with an
Autonomous Dynamical System (DS)
Velocity Position Target
Variables
Target
1x
2x
x
Lyapunov Theorem for
Global Asymptotic Stability
How to ensure convergence to
the desired target?
2

4. Global Asymptotic Stability of
Autonomous Dynamical System (DS)
Lyapunov Function ~ Energy-like Function
Theorem A DS is globally asymptotically stable at iff
there exists a Lyapunov candidate function
that is radially unbounded; i.e. and
satisfies the following conditions:
V should be non-increasing along all trajectories.
Lyapunov’s Theorem for Global Asymptotic Stability
3

5. Lyapunov’s Theorem for Global Asymptotic Stability
Level Sets of Lyapunov Function
Theorem A DS is globally asymptotically stable at iff
there exists a Lyapunov candidate function
that is radially unbounded; i.e. and
satisfies the following conditions:
V should be non-increasing along all trajectories.
Global Asymptotic Stability of
Autonomous Dynamical System (DS)
4
Obtuse Angle

6. Stability of a Linear Autonomous Dynamical System (DS)
Quadratic Lyapunov Function (QLF)
How to ensure is always negative?
Enforce the eigenvalues to be negative! 5

7. Stability of a Linear Autonomous Dynamical System (DS)
Parametrized Quadratic Lyapunov Function (P-QLF)
Enforce the eigenvalues to be negative!
What if f(x) is non-linear?
Stability not easy to define: local linearization;
numerical estimation of stability;
analytical solution in special cases. 6

8. Representing Non-linear Motions as Mixtures of Linear DS
7
2-nd Linear DS
4-th Linear DS Activation/Mixing
function for 2-nd DS
Activation/Mixing
function for 4-th DS
How do we learn all of
these parameters?

9. 8
Learning Non-linear DS via Gaussian Mixture Regression
Take a density based approach to modeling dynamical systems
Given a set of demonstrations, learn the joint density via GMM
2D projection of a
normal distribution
   ~ ; ,p x N x  

10. 9
Learning Non-linear DS via Gaussian Mixture Regression
Through a slight change of variables To ensure Global Asymptotic Stability
Khansari Zadeh, S. M. and Billard, A. (2011) IEEE Transactions on Robotics
We estimate the Gaussian parameters via constraint-
based optimization with stability constraints.
Stability Constraints

11. 10
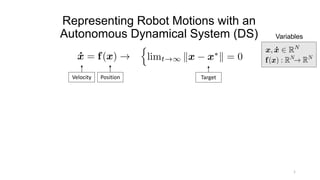
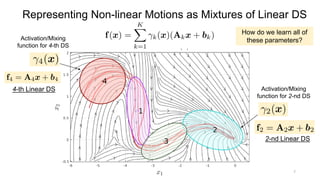
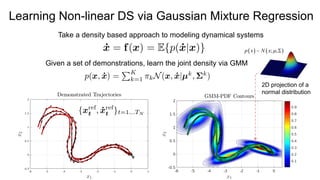
Learning Non-linear DS via Gaussian Mixture Regression
[1] Khansari Zadeh, S. M. and Billard, A. (2011) IEEE Transactions on Robotics
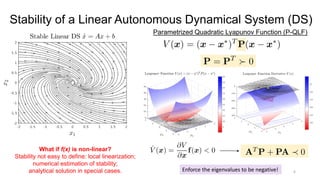
Stable Estimator of Dynamical Systems (SEDS) Approach [1]
Demonstrations
Reproductions

12. 11
SEDS in Action
Khansari Zadeh, S. M. and Billard, A. (2011) IEEE Transactions on Robotics
Demonstrations of Point-to-Point Motions Execution of Learned DS Motions

13. 12
SEDS in Action
[2] Figueroa, Pais and Billard. (2016) ACM/IEEE HRI Conference
Demonstrations of Sequence of Point-to-Point Motions Execution of Sequence of Learned DS Motions
Learn a point-to-point SEDS for each Phase + impedance/force profiles [2]

14. 13
Limitations of SEDS Approach
 Optimal number of K Gaussian components has to be set manually or ‘empirically’
 Cannot handle highly non-linear motions:
Why can’t we model these trajectories accurately?

15. 14
These trajectories violate this condition
QLF is too conservative.
Acute Angles!
Can we do better?

16. 16
Acute Angles!
Use Parametrized Quadratic
Lyapunov Function (P-QLF)!
These trajectories violate this condition
QLF is too conservative.
Acute Angles!

17. 17
Learning Non-linear DS via GMMs with P-QLF
We decouple the density estimation from the DS parameters
Given a set of demonstrations, learn the
GMM density on position variables only Solve a constrained optimization problem
Stability Constraints
Ensure Stability with P-QLF

18. 18
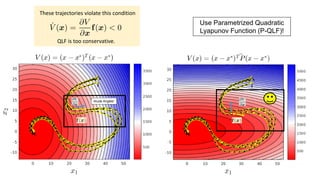
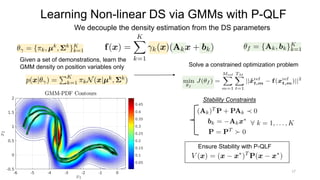
Learning Non-linear DS via GMMs with P-QLF
[3] Mirrazavi, BIllard. (2018) EPFL PhD Thesis.
Linear Parameter Varying (LPV) Dynamical Systems (DS) Approach [2]

19. 19
Outperforms SEDS in Reproduction Accuracy

20. 20
Outperforms SEDS in Reproduction Accuracy

21. 21
Limitations of LPV-DS Approach
 Optimal number of K Gaussian components has to be set manually or ‘empirically’
 Very sensitive to GMM fit:
Good GMM fit

22. 22
Limitations of LPV-DS Approach
 Optimal number of K Gaussian components has to be set manually or ‘empirically’
 Very sensitive to GMM fit:
Bad GMM fit

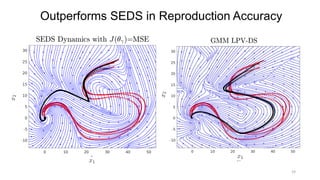
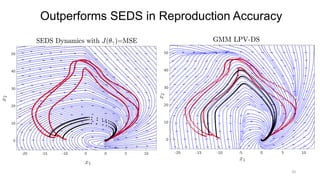
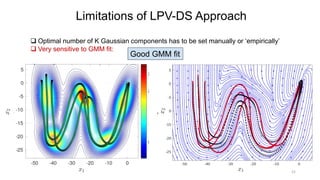
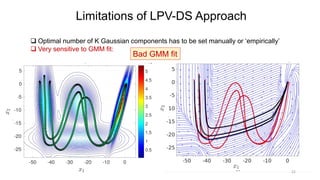
23. Other SEDS-based Extensions – beyond QLF
Tau-SEDS Approach [4]:
Based on Diffeomorphic Transformations
And Complex Lyapunov Functions
23[4] Neumann, Steil (2015) Robotics and Autonomous Systems
Step 1: Construct a Lyapunov Candidate
Function Consistent with the Demonstrations
Weighted Sum of Asymmetric
Quadratic Functions (WSAQF) [5]
[5] Khansari, Billard (2015) Robotics and Autonomous Systems

24. Other SEDS-based Extensions – beyond QLF
Tau-SEDS Approach [4]:
Based on Diffeomorphic Transformations
And Complex Lyapunov Functions
24
Step 2: Define a diffeomorphism where
takes the form of a QLF
Step 3: Transform the demonstrations via
Step 4: Learn SEDS on transformed data.
Step 1: Construct a Lyapunov Candidate
Function Consistent with the Demonstrations
[4] Neumann, Steil (2015) Robotics and Autonomous Systems [5] Khansari, Billard (2015) Robotics and Autonomous Systems

25. Other SEDS-based Extensions – beyond QLF
Tau-SEDS Approach [4]:
Based on Diffeomorphic Transformations
And Complex Lyapunov Functions
25
Step 2: Define a diffeomorphism where
takes the form of a QLF
Step 3: Transform the demonstrations via
Step 4: Learn SEDS on transformed data.
Step 5: Back-transform learn SEDS via
Step 1: Construct a Lyapunov Candidate
Function Consistent with the Demonstrations
[4] Neumann, Steil (2015) Robotics and Autonomous Systems [5] Khansari, Billard (2015) Robotics and Autonomous Systems

26. Other SEDS-based Extensions – beyond QLF
26
Contracting Dynamical Systems Primitives [5]
[6] Ravichandar, Salehi, Dani (2017) CoRL
Stability Constraints via
Partial Contraction Theory

27. Full List of Publications Mentioned in Lecture
27
[1] Khansari Zadeh, S. M. and Billard, A. (2011) Learning Stable Non-Linear Dynamical Systems with Gaussian
Mixture Models. IEEE Transaction on Robotics, vol. 27, num 5, p. 943-957.
[2] Figueroa, N., Pais, A. L. and Billard, A. (2016) Learning Complex Sequential Tasks from Demonstration: A
Pizza Dough Rolling Case Study. In Proc. of the 2016 ACM/IEEE International Conference on Human-Robot
Interaction. HRI Pioneers Workshop.
[3] Mirrazavi Salehian, S. S. (2018) Compliant control of Uni/ Multi- robotic arms with dynamical systems.
PhD Thesis.
[4] K. Neumann and J. J. Steil. (2015) Learning robot motions with stable dynamical systems under
diffeomorphic transformations. Robotics and Autonomous Systems, 70 (Supplement C):1 – 15
[5] Khansari Zadeh, S. M. and Billard, A. (2014) Learning Control Lyapunov Function to Ensure Stability of
Dynamical System-based Robot Reaching Motions. Robotics and Autonomous Systems
[6] H. Ravichandar, I. Salehi, and A. Dani. (2017) Learning partially contracting dynamical systems from
demonstrations. In Proceedings of the 1st Annual Conference on Robot Learning, vol. 78 of Proceedings of
Machine Learning Research, pp 369–378

28. Exercise Session 1
28
Selection of
number of
Gaussians
Selection of
Objective
Function

29. Exercise Session 1
29
Selection of
number of
Gaussians
Selection of
Optimization
Variant

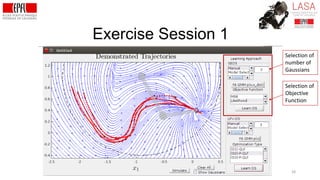
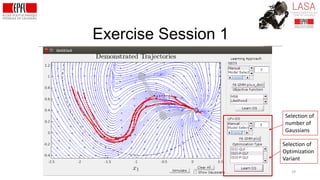
30. Exercise Session 1
30
Selection of
Optimization
Variant
P is unknown, is estimated jointly with A’s.
P is known, it is estimated a priori via [5]
[5] Khansari, Billard (2015) Robotics and Autonomous Systems