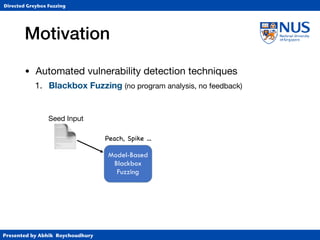
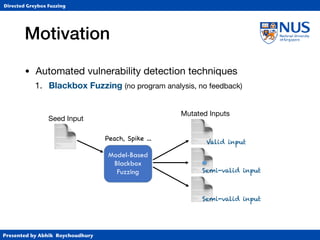
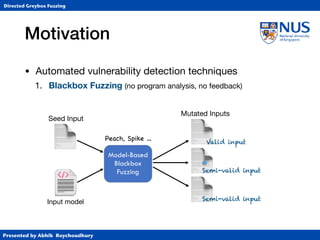
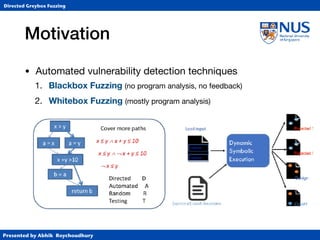
This document summarizes a PhD thesis defense presentation on directed greybox fuzzing. It discusses:
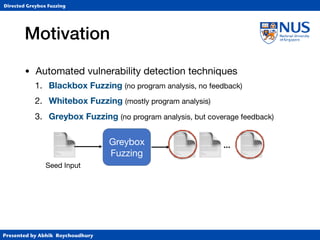
1. Different types of fuzzing techniques including blackbox, whitebox, and greybox fuzzing.
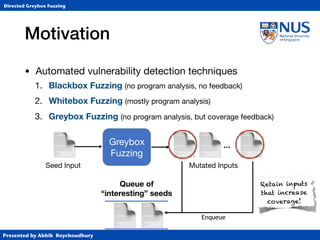
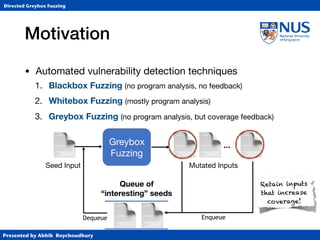
2. How directed greybox fuzzing formulates the problem of reaching targeted locations as an optimization problem rather than using heavy symbolic execution.
3. The instrumentation process to compute distance metrics to target locations and guide input generation towards minimizing distance.









![Presented by Abhik Roychoudhury
Directed Greybox Fuzzing
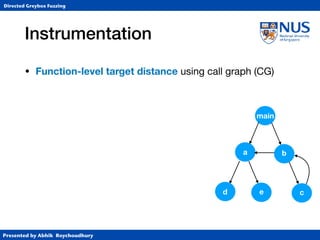
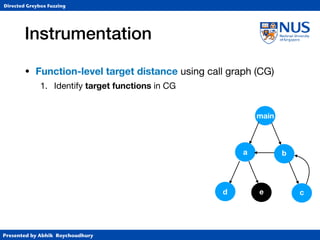
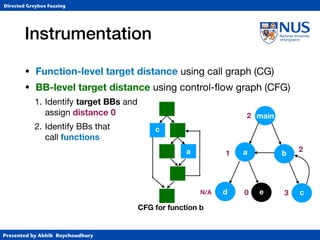
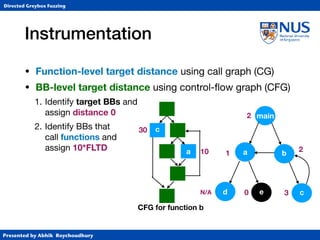
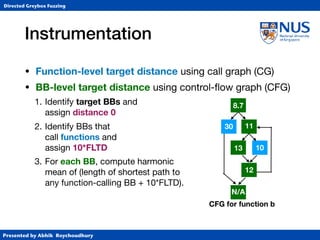
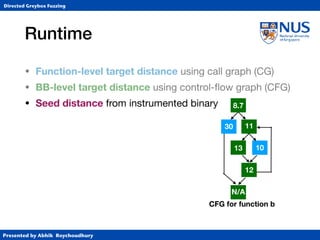
Instrumentation
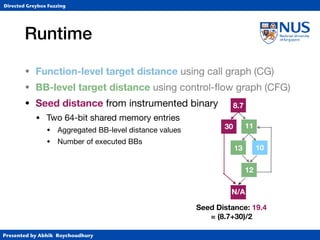
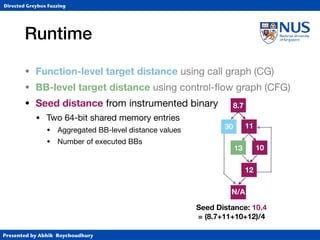
• Function-level target distance using call graph (CG)
• BB-level target distance using control-flow graph (CFG)
1. Identify target BBs and
assign distance 0
2. Identify BBs that
call functions and
assign 10*FLTD
3. For each BB, compute harmonic
mean of (length of shortest path to
any function-calling BB + 10*FLTD).
CFG for function b
c
a 10
30
[(1+30)-1+(2+10)-1]-1](https://image.slidesharecdn.com/ccs17-190819235830/85/AFLGo-Directed-Greybox-Fuzzing-24-320.jpg)










![Presented by Abhik Roychoudhury
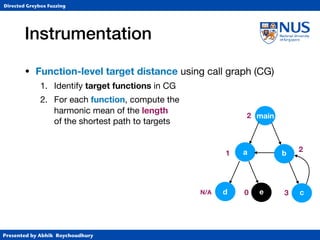
Directed Greybox Fuzzing
Directed Fuzzing as
Optimisation Problem
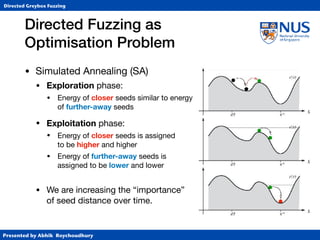
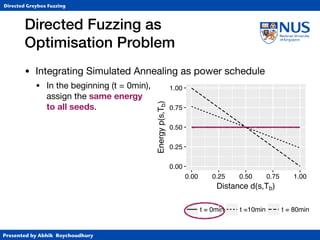
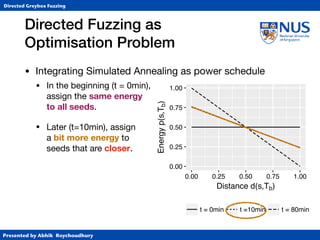
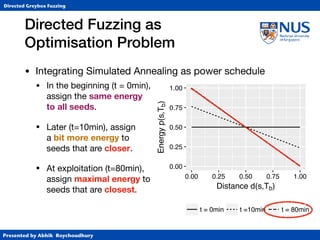
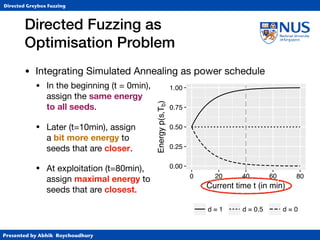
• Simulated Annealing (SA)
• Annealing from metallurgy: control the cooling of material
to reduce defects (e.g., cracks or bubbles) in the material.
• Temperature T ∈ [0,1] specifies “importance” of distance.
• At T=1, exploration (normal AFL)
• At T=0, exploitation (gradient descent)
• Cooling schedule controls (global) temperature
• Classically, exponential cooling.](https://image.slidesharecdn.com/ccs17-190819235830/85/AFLGo-Directed-Greybox-Fuzzing-42-320.jpg)

![Presented by Abhik Roychoudhury
Directed Greybox Fuzzing
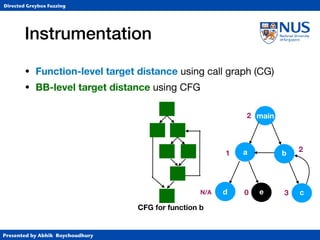
Results
• Patch Testing: Reach changed statements
• State-of-the-art in patch testing
• KATCH (based on Klee symbolic exec. tool)
• Patch Coverage (#changed BBs reached)
is unrelated to the concept [32]. We make a conscious eort to
explain the observed phenomena and distinguish conceptual from
technical origins. Moreover, we encourage the reader to consider
the perspective of a security researcher who is actually handling
these tools to establish whether there exists a vulnerability.
5.1 Patch Coverage
We begin by analyzing the patch coverage achieved by both K
and AFLG as measured by the number of previously uncovered
basic blocks that were changed in the respective patch.
Table 1: Patch coverage results showing the number of previ-
ously uncovered targets that K and AFLG could cover
in the stipulated time budget, respectively.
#Changed #Uncovered
Basic Blocks Changed BBs K AFLG
Binutils 852 702 135 159
Diutils 166 108 63 64
Sum 1018 810 198 223
complex inp
executed onl
for certain a
dened stru
higher-quali
approach [2
To unders
we investiga
we can see
cannot cove
cover. We at
vidual streng
dicult con
be dicult t
quickly exp
stuck in a pa
AFLG and
282 targets
cover indi](https://image.slidesharecdn.com/ccs17-190819235830/85/AFLGo-Directed-Greybox-Fuzzing-48-320.jpg)
![Presented by Abhik Roychoudhury
Directed Greybox Fuzzing
Results
• Patch Testing: Reach changed statements
• State-of-the-art in patch testing
• KATCH (based on Klee symbolic exec. tool)
• Patch Coverage (#changed BBs reached)
• While we would expect Klee to take a substantial lead,
AFLGo outperforms KATCH in terms of patch coverage.
is unrelated to the concept [32]. We make a conscious eort to
explain the observed phenomena and distinguish conceptual from
technical origins. Moreover, we encourage the reader to consider
the perspective of a security researcher who is actually handling
these tools to establish whether there exists a vulnerability.
5.1 Patch Coverage
We begin by analyzing the patch coverage achieved by both K
and AFLG as measured by the number of previously uncovered
basic blocks that were changed in the respective patch.
Table 1: Patch coverage results showing the number of previ-
ously uncovered targets that K and AFLG could cover
in the stipulated time budget, respectively.
#Changed #Uncovered
Basic Blocks Changed BBs K AFLG
Binutils 852 702 135 159
Diutils 166 108 63 64
Sum 1018 810 198 223
complex inp
executed onl
for certain a
dened stru
higher-quali
approach [2
To unders
we investiga
we can see
cannot cove
cover. We at
vidual streng
dicult con
be dicult t
quickly exp
stuck in a pa
AFLG and
282 targets
cover indi](https://image.slidesharecdn.com/ccs17-190819235830/85/AFLGo-Directed-Greybox-Fuzzing-49-320.jpg)

![Presented by Abhik Roychoudhury
Directed Greybox Fuzzing
Results
• Patch Testing: Reach changed statements
• State-of-the-art in patch testing
• KATCH (based on Klee symbolic exec. tool)
• Patch Coverage (#changed BBs reached)
• Vulnerability Detection (#errors discovered)
As future work, we are planning to integrate symbolic-execution-
based directed whitebox fuzzing and directed greybox fuzzing to
achieve a directed fuzzing technique that is both very eective and
very ecient in terms of reaching pre-specied target locations.
We believe that such an integration would be superior to each
technique individually. An integrated directed fuzzing technique
that leverages both symbolic execution and search as optmization
problem would be able to draw on their combined strengths to
mitigate their indiviual weaknesses. Driller [38] is an example of
an (undirected) fuzzer that integrates the AFL greybox fuzzer and
the K whitebox fuzzer.
5.2 Vulnerability Detection
Table 2: Showing the number of previously unreported bugs
found by AFLG (reported Apr’2017) in addition to the num-
ber of bug reports for K (reported Feb’2013).
K AFLG
#Reports #Reports14 #New Reports #CVEs
Binutils 7 4 12 7
Diutils 0 N/A 1 0
Sum 7 4 13 7
AFLG found 13 previously unreported bugs in addition to 4 of
Table 3: Bug rep
Report-ID
Binutils
21408
21409
21412
21414
21415
21417
Diutils http://lists.g
We attribute m
to the eciency of
program analysis a
magnitute more in
is the runtime che
error detection mec
the program when
we instrumented o
Sanitizer (ASAN). I
e.g., by reading be
writing memory th
a SEGFAULT even
fuzzer uses this sig
for a generated in
(i.e., interprets) th
and uses constrain](https://image.slidesharecdn.com/ccs17-190819235830/85/AFLGo-Directed-Greybox-Fuzzing-51-320.jpg)
![Presented by Abhik Roychoudhury
Directed Greybox Fuzzing
Results
• Patch Testing: Reach changed statements
• State-of-the-art in patch testing
• KATCH (based on Klee symbolic exec. tool)
• Patch Coverage (#changed BBs reached)
• Vulnerability Detection (#errors discovered)
• AFLGo found 13 previously unreported bugs (7 CVEs)
in addition to 4 of the 7 bugs that were found by KATCH.
As future work, we are planning to integrate symbolic-execution-
based directed whitebox fuzzing and directed greybox fuzzing to
achieve a directed fuzzing technique that is both very eective and
very ecient in terms of reaching pre-specied target locations.
We believe that such an integration would be superior to each
technique individually. An integrated directed fuzzing technique
that leverages both symbolic execution and search as optmization
problem would be able to draw on their combined strengths to
mitigate their indiviual weaknesses. Driller [38] is an example of
an (undirected) fuzzer that integrates the AFL greybox fuzzer and
the K whitebox fuzzer.
5.2 Vulnerability Detection
Table 2: Showing the number of previously unreported bugs
found by AFLG (reported Apr’2017) in addition to the num-
ber of bug reports for K (reported Feb’2013).
K AFLG
#Reports #Reports14 #New Reports #CVEs
Binutils 7 4 12 7
Diutils 0 N/A 1 0
Sum 7 4 13 7
AFLG found 13 previously unreported bugs in addition to 4 of
Table 3: Bug rep
Report-ID
Binutils
21408
21409
21412
21414
21415
21417
Diutils http://lists.g
We attribute m
to the eciency of
program analysis a
magnitute more in
is the runtime che
error detection mec
the program when
we instrumented o
Sanitizer (ASAN). I
e.g., by reading be
writing memory th
a SEGFAULT even
fuzzer uses this sig
for a generated in
(i.e., interprets) th
and uses constrain](https://image.slidesharecdn.com/ccs17-190819235830/85/AFLGo-Directed-Greybox-Fuzzing-52-320.jpg)

![Presented by Abhik Roychoudhury
Directed Greybox Fuzzing
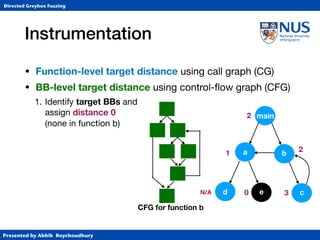
Results
• Crash Reproduction: Exercise stack trace
• State-of-the-art in crash reproduction
• BugRedux (based on Klee symbolic exec. tool)
• Experimental Setup
• Reuse original BugRedux-benchmark
• Determine whether or not crash can be reproduced
experimental setup, starting conguration, and timeouts. BugRedux
[18] is a directed whitebox fuzzer based on K, takes as input a
sequence of program statements, and generates as output a test case
that exercises that sequence and crashes the program. It was shown
that BugRedux works best of the complete method-call sequence is
provided that lead to the crash. However, as discussed earlier often
only the stack-trace is available, which does not contain methods
that have already “returned”, i.e., nished execution. Hence, for our
comparison, we set the method-calls in the stack trace as targets.
Despite our request for all subjects from the original dataset, only
a subset of nine subjects could be located for us. For two subjects
(exim, xmail), we could not obtain the stack-trace that would specify
the target locations. Specically, the crash in exim can only be
reproduced on 32bit architectures while the crash in xmail overows
the stack such that the stack-trace is overridden. The results for the
remaining seven subjects are shown in Table 6.
Table 6: Bugs reproduced for the original BugRedux subjects
Subjects BugRedux AFLG Comments
sed.fault1 7 7 Takes two les as input
sed.fault2 7 3
grep 7 3
gzip.fault1 7 3
gzip.fault2 7 3
ncompress 3 3
polymorph 3 3
same benchmarks that th
in the original papers [18
The second concern is
a study minimizes system
nal validity for fuzzer exp
However, for our experi
was readily available, suc
Binutils and the K ex
OSS-Fuzz experiments, a
classically provides for th
when comparing two fuzz
seed corpus such that bot
Second, like implementati
faithfully implement the
shown in the comparison
The third concern is co
a test measures what it c
note that results of tool co
grain of salt. An empirical
implementations of two c
selves. Improving the ec
fuzzer may only be a que
lated to the concept [32].
explain the observed phen
technical origins. Moreov
the perspective of a secur
these tools to establish w
AFLGo reproduces
3 times more crashes!](https://image.slidesharecdn.com/ccs17-190819235830/85/AFLGo-Directed-Greybox-Fuzzing-54-320.jpg)


