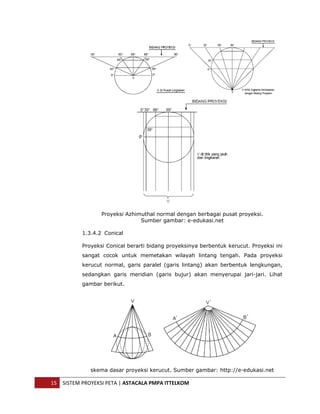
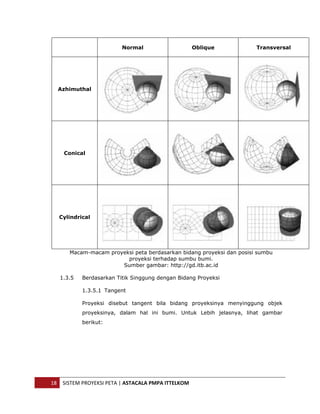
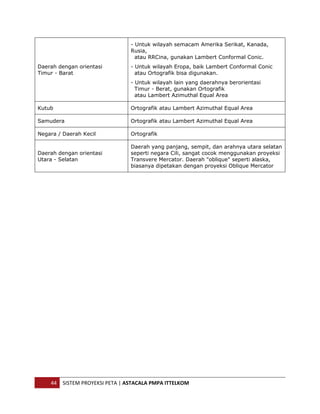
Dokumen ini membahas sistem proyeksi peta yang merupakan cara untuk menggambarkan permukaan bumi yang berbentuk tiga dimensi ke dalam bentuk dua dimensi pada media peta. Penjelasan mencakup teknik dasar proyeksi, referensi ellipsoid, datum geodetik, dan pembagian sistem proyeksi berdasarkan berbagai kriteria. Distorsi dalam proyeksi tidak dapat dihindari dan memerlukan pemilihan teknik yang tepat sesuai dengan karakteristik daerah yang akan dipetakan.

1.
6/02/2009
ARIEF TJAHYADI SISTEM PROYEKSI PETA
ASTACALA
PERHIMPUNAN MAHASISWA PECINTA ALAM ITTELKOM

2.
Daftar Isi
Daftar Isi .............................................................................................................. ii
Sistem Proyeksi Peta........................................................................................... 3
1.1 Teknik Dasar Proyeksi Peta .............................................................. 5
1.1.1 Referensi Ellipsoid ............................................................... 6
1.1.2 Datum Geodetik .................................................................. 8
1.1.3 Penentuan Teknik Proyeksi ................................................... 9
1.2 Pembagian Sistem Proyeksi .............................................................. 10
1.3 Sistem Proyeksi .............................................................................. 11
1.3.1 Berdasarkan Sifat yang Dipertahankan ................................... 11
1.3.1.1 Proyeksi Ekuivalen ................................................. 11
1.3.1.2 Proyeksi Konform ................................................... 11
1.3.1.3 Proyeksi Ekuidistan ................................................ 11
1.3.2 Berdasarkan Cara Penurunan Peta ......................................... 11
1.3.2.1 Proyeksi Geometris ................................................ 11
1.3.2.2 Proyeksi Matematis ................................................ 11
1.3.2.3 Proyeksi Semi Geometris......................................... 11
1.3.3 Berdasarkan Posisi Sumbu Proyeksi ....................................... 12
1.3.3.1 Normal ................................................................. 12
1.3.3.2 Transversal ........................................................... 12
1.3.3.3 Oblique................................................................. 12
1.3.4 Berdasarkan Media Proyeksi ................................................. 13
1.3.4.1 Azhimuthal............................................................ 13
1.3.4.2 Conical ................................................................. 15
1.3.4.3 Cylindrical ............................................................. 16
1.3.5 Berdasarkan Titik Singgung dengan Bidang Proyeksi ................ 18
1.3.5.1 Tangent ................................................................ 18
1.3.5.2 Secant.................................................................. 19
1.4 Proyeksi Gubahan (Arbitraty)............................................................ 19
1.4.1 Berdasarkan Proyeksi Azimuthal ............................................ 19
1.4.1.1 Azimuthal Equidistant ............................................. 19
1.4.1.2 Lambert Azimuthal Equal Area ................................. 21
1.4.1.3 Orthographic ......................................................... 22
1.4.1.4 Stereographic ........................................................ 24
1.4.2 Berdasarkan Proyeksi Kerucut (Conical).................................. 25
1.4.2.1 Proyeksi Albers Equal Area Conic .............................. 25
1.4.2.2 Equidistant Conic ................................................... 26
1.4.2.3 Lambert Conformal Conic ........................................ 26
1.4.2.4 Polyconic .............................................................. 28
1.4.3 Berdasarkan Proyeksi Slinder ................................................ 29
1.4.3.1 Mercator ............................................................... 29
1.4.3.2 Transverse Mercator ............................................... 30
1.4.3.3 Universal Transverse Mercator ................................. 31
1.4.3.4 Oblique Mercator.................................................... 36
1.4.3.5 Space Oblique Mercator .......................................... 37
1.4.3.6 Cylindrical Equal Area ............................................. 38
1.4.3.7 Miller Cylindrical .................................................... 39
1.4.4 Proyeksi Pseudocylindrical (Slinder Semu) .............................. 40
1.4.4.1 Proyeksi Mollweide ................................................. 40
1.4.4.2 Proyeksi Sinusoidal Equal Area ................................. 41
1.4.4.3 Proyeksi Robinson .................................................. 42
1.5 Penggunaan Proyeksi ...................................................................... 43
Maraji' 45
ii

3.
Sistem Proyeksi Peta
oleh: Arief Tjahyadi (A - 008 - PR) *
Proyeksi adalah suatu cara untuk menyajikan suatu objek dengan bentuk dan dimensi
tertentu ke dalam bentuk dan dimensi lain. Proyeksi peta berarti cara untuk mengkonversi
posisi tiga dimensi dari suatu titik di permukaan bumi ke representasi posisi dua dimensi
pada media peta.
Sistem proyeksi peta berarti segala hal (termasuk model matematis) yang menyangkut
penggambaran permukaan bumi pada media dua dimensi. Singkatnya, proyeksi peta berarti
cara untuk menggambarkan bumi yang berbentuk bulat ke atas media yang datar, seperti
kertas.
Dari segi bentuk, mungkin representasi terbaik bagi bumi adalah globe. Pada globe, arah,
bentuk, luas, serta jarak memiliki nilai perbandingan yang benar dengan kondisi
sesungguhnya. Namun globe memiliki keterbatasan di sisi dimensi, sebab tak mungkin
membuat globe yang berisi informasi secara detil karena skalanya terlalu kecil. Lagipula,
globe tidak nyaman untuk dibawa-bawa, disamping ongkos pembuatan dalam skala massal
yang relatif mahal.
Sistem proyeksi peta yang baik harus memenuhi beberapa kriteria seperti:
Bentuk yang terdapat di atas permukaan bumi tidak mengalami perubahan, persis
seperti pada gambar peta di globe bumi. Bentuk kepala burung di muka bumi,
setelah diproyeksikan ke selembar peta harus berbentuk kepala burung juga, bukan
menjadi kepala unta
Luas permukaan tidak berubah (setelah memperhitungkan faktor skala)
Jarak antar titik di atas permukaan bumi yang diproyeksikan harus tetap (setelah
memperhitungkan faktor skala)
Arah dan sudut antara titik yang satu dengan yang lain harus tetap dan tidak
mengalami perubahan sedikitpun (setelah memperhitungkan faktor skala).
Ini menimbulkan persoalan tersendiri, sebab teknik proyeksi ke bidang datar tidak
memungkinkan untuk memenuhi seluruh prasyarat tersebut. Sebagai ilustrasi, perhatikan
gambar berikut:

4.
Prinsip proyeksi berupa pembuatan peta dari bentuk bola (globe) ke bidang datar (peta).
Sumber gambar: http://e-edukasi.net
Dari gambar di atas, dapat dilihat perubahan dari posisi titik di globe ke bidang datar,
seperti gambar berikut:
Perubahan dari posisi titik di globe ke bidang datar.
Sumber gambar: http://e-edukasi.net
Ini menunjukkan adanya distorsi (cacat) pada gambar yang dihasilkan, karena jarak A — B
menjadi lebih panjang dari yang seharusnya. Sedangkan jarak C — D menjadi lebih pendek.
Agar lebih jelas, perhatikan "irisan" bola bumi ke dalam bentuk bidang datar sebagai
berikut:
4 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

5.
Irisan bumi menjadi bidang datar. Sumber gambar: http://e-edukasi.net
Terlihat dari gambar tersebut, bahwa mustahil untuk memetakan bumi ke bidang datar
secara utuh dan sempurna.
Maka berkembanglah berbagai teknik dari sistem proyeksi peta yang masing-masing
memiliki kelebihan dan kekurangan. Proyeksi yang baik untuk memetakan wilayah kutub,
belum tentu baik pula saat diterapkan di wilayah ekuator. Maka distorsi pada proyeksi peta
merupakan sesuatu yang tidak mungkin terhindarkan.
1.1 Teknik Dasar Proyeksi Peta
Sebelum melakukan proyeksi peta, terlebih dahulu harus dibuat atau diasumsikan sebuah
model bagi bumi. Hal ini dilakukan karena bumi tidak berbentuk bulat sempurna, melainkan
lebih mendekati bentuk telur (ellipsoid) dengan permukaan yang tidak rata. Istilah Ellipsoid
ini sinonim dengan Spheroid yang dipakai untuk menyatakan bentuk bumi. Karena bumi
tidak uniform (tidak seragam permukaannya), maka terkadang digunakanlah istilah Geoid
untuk menyatakan bentuk Ellipsoid yang tidak rata. Selain itu, bentuk bumi di daerah
khatulistiwa lebih menggelembung dibandingkan daerah kutub yang justru cenderung datar.
Diameter di khatulistiwa ternyata lebih besar daripada di kutub.
Maka untuk keperluan proyeksi peta, dibuatlah suatu model yang mendekati bentuk bumi.
Model ini disebut Ellipsoid Referensi (Refference Ellipsoid). Ada bermacam model yang telah
dibuat. Model yang dipilih ini akan menjadi acuan bagi pengambilan data yang diperlukan
untuk melakukan proyeksik peta. Lihat gambar berikut:
5 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

6.
Tahapan proyeksi peta. Sumber gambar: http://gd.itb.ac.id
Setelah model ini dibuat, barulah dilakukan tahapan proyeksi selanjutnya. Tahapan proyeksi
yang penuh perhitungan matematis dengan berbagai persamaan trigonometri dan
pemahaman geometri itu tidak akan dibahas di sini.
1.1.1 Referensi Ellipsoid
Referensi Elpsoid adalah model matematis bumi. Model ini terdiri dari tiga
parameter, yaitu jari-jari kutub, jari-jari ekuator, serta kerataan atau kegepengan
(flattening).
Secara matematis, model ini dapat dituliskan sebagai berikut:
a = jari-jari ekuator = sumbu panjang
b = jari-jari kutub = sumbu pendek
f = kerataan (kegepengan) = flattening = (a - b) / a
6 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

7.
b = Sumbu Pendek
Semi Minor Axis
b
a = Sumbu Panjang
Semi Major Axis
a
f = Fattening
= Kerataan
Ellipsoid Referensi.
Ellipsoid Referensi ini digunakan untuk menentukan Datum, yaitu titik referensi
pengukuran yang diguanakan dalam pemetaan skala besar. Sampai saat ini, jumlah
Ellipsoid Referensi yang sudah dibuat tidaklah sedikit dan memiliki nilai parameter
yang tidak sama. Berikut beberapa contohnya:
Tabel 1. Beberapa Ellipsoid Referensi
SemiMajor Axis
Nama Ellipsoid (a) 1/f
(meter)
Bessel 1841 6377397,155 299,1528128
Clarke 1866 6378206,4 294,9786982
6377276.345
Everest (India 1830) 300,8017
Everest (India 1956) 6377301.243 300,8017
Everest (Pakistan) 6377309.613 300,8017
WGS 72 6378135 298,26
Indonesian 1974 6378160 298,247
GRS 80 6378137 298,257222101
WGS 84 6378137 298,257223563
Dan Lain-Lain
Pengukuran untuk pembuatan Ellipsoid Referensi semakin akurat karena kemajuan
teknologi. Hingga saat ini WGS 84 dianggap sebagai Ellipsoid Referensi yang
terbaik. Konon, rasio penyimpangannya hanya 1/100.000 saja (-100 meter hingga
+60 meter). Dari Ellipsoid Referensi yang ada ini, ditentukanlah Datum Geodetik
yang akan digunakan untuk melakukan pemetaan.
7 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

8.
1.1.2 Datum Geodetik
Pemilihan sistem koordinat dengan mengadopsi suatu bentuk ellipsoid serta
menetapkan posisi dan orientasi ellipsoid tersebut terhadap Bumi, dinamakan
Datum Geodetik. Ellipsoid Referensi yang dipilih adalah yang dianggap paling
akurat, sesuai, atau yang terbaik untuk daerah obyek pemetaan (paling mendekati
kenyataan). Datum Geodetik merupakan acuan untuk melakukan proyeksi bumi
pada suatu daerah tertentu . Maka tiap satu daerah dengan daerah lain, bisa saja
memiliki datum geodetik yang berbeda saat melakukan proyeksi peta. Dalam
sejarah pemetaan di Indonesia, telah terjadi beberapa kali perubahan datum
geodetik yang digunakan.
Pertama, untuk penggunaan sejak tahun 1870 (oleh pemerintah kolonial Belanda)
hingga tahun 1974, Datum Geodetik menggunakan Ellipsoid Bessel 1851
(a : 6.377.563 m ; f : 1/299,3) dan sistem koordinat relatif dan posisi Ellipsoid
bermacam-macam. Untuk Jawa - Nusa Tenggara - Sumatera dipakai titik di Gunung
Genuk, di sekitar Semarang sebagai titik awal sistem (berhimpitan dengan titik
Gunung Genuk di Jawa Tengah) dan dinamakan Datum Genuk. Di Kalimantan ada 2
datum, yaitu Datum Gunung Raya di Kalimantan Barat dan Datum Serindung di
Kalimantan Timur (keduanya terpisah). Untuk Sulawesi dipakai Datum
Monconglowe di Sulawesi Selatan. Selain itu juga ada beberapa datum di Maluku
dan di Papua.
Datum yang terpisah-pisah ini membuat sistem geografis menjadi terpisah-pisah
juga, sehingga menyulitkan kita membangun suatu Sistem Informasi Geografis
yang integratif. Hal ini akibat penggunaan teknologi pengukuran optik (yang
mengukur sudut-sudut antara titik-titik di Bumi dalam suatu jaringan Triangulasi
atau jaringan sudut segi tiga) yang tidak memungkinkan pengukuran langsung
untuk menghubungkan posisi antara pulau-pulau yang berjauhan. Jarak yang dapat
diukur antara 2 titik dengan pengukuran optik maksimum 60 km jika anda berada
di atas gunung 3.000 m dpl tingginya. Lebih dari itu, teknologi ini tidak memadai
lagi.
Kedua, dalam program Pemetaan Dasar Nasional yang dimulai pada masa Repelita
I (1960-1974). Ini bertepatan dengan dibentuknya Badan Koordinasi Survei dan
Pemetaan Nasional (Bakosurtanal) pada tahun 1969, dan dimulainya program
penyatuan sistem referensi. Tujuan utamanya untuk membangun sistem informasi
8 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

9.
geografis yang integratif di Indonesia. Pada masa ini teknologi pun telah
berkembang dengan munculnya penentuan posisi dengan satelit, yang pada waktu
itu dinamakan Sistem Satelit Doppler dari US Navy Navigation Satellite System
(NNSS). Sistem triangulasi yang digunakan pada masa sebelumnya telah
ditinggalkan.
Dengan teknologi ini seluruh datum Indonesia yang terpisah telah disatukan ke
dalam satu sistem, walaupun pada waktu itu kita masih mengadopsi sistem relatif
terhadap satu titik di muka Bumi yang dipakai sebagai acuan. Untuk itu
Bakosurtanal memutuskan untuk memilih satu titik triangulasi di Padang sebagai
titik awal sistem dan dinamakan Datum Padang. Kemudian Datum Padang ini
dinamakan dengan nama baku yang terkait dengan tahun penetapannya, yaitu
Datum Indonesia 1974 (Indonesian Datum 1974 atau ID-74).
Dalam datum tunggal ini Indonesia mengganti ellipsoid Bessel 1841 dengan
ellipsoid yang diadopsi secara internasional pada waktu itu, yaitu GRS 1967
(Geodetic Reference System 1967) dengan nilai a : 6.378.160 m dan f : 1/298,25.
Ketiga, ketika setelah berkembangnya teknologi GPS (Global Positioning System),.
Pada masa ini penentuan posisi yang lebih akurat dapat dicapai setiap saat dan
tempat. Agar peta-peta Indonesia tetap bisa digunakan, maka perlu mengubah
datum yang digunakan dari ID-74 ke datum yang sesuai dengan sistem GPS.
Datum baru ini dinamakan Datum Geodesi Nasional Indonesia 1995 (DGNI 1995)
dengan ellipsoid acuan WGS 1984 (a : 6.378.137 m dan kegepengan f = 1/295,34)
yang juga digunakan secara internasional, serta sistem koordinat geosentrik.
Datum ini mengadopsi sitem datum geodetik absolut dengan mengatur pusat ER
berimpit dengan pusat masa bumi dan tidak digunakan lagi Datum Padang (yang
merupakan datum relatif) seperti pada masa sebelumnya.
1.1.3 Penentuan Teknik Proyeksi
Tahap selanjutnya setelah Datum Geodetiknya ditentukan adalah menentukan
teknik proyeksi yang akan digunakan. Ada berbagai macam teknik proyeksi yang
bisa dibedakan berdasarkan bidang proyeksi, titik singgung proyeksi, sifat asli yang
dipertahankan, serta posisi sumbu proyeksinya.
9 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

10.
Cara proyeksi peta bisa dipilah sebagai:
Proyeksi langsung (direct projection): Dari ellipsoid langsung ke bidang
proyeksi.
Proyeksi tidak langsung (double projection): Proyeksi dilakukan
menggunakan "bidang" antara, ellipsoid ke bola dan dari bola ke bidang
proyeksi.
Pemilihan sistem proyeksi peta ditentukan berdasarkan pada:
Ciri-ciri tertentu atau ciri asli yang ingin dipertahankan, sesuai dengan
tujuan pembuatan / pemakaian peta
Ukuran dan bentuk daerah yang akan dipetakan
Letak daerah yang akan dipetakan.
Sesudah sistem proyeksi dipilih, barulah dilakukan proyeksi dan pemetaannya. Penjelasan
mengenai berbagi teknik proyeksi ini dijelaskan dalam bagian selanjutnya.
1.2 Pembagian Sistem Proyeksi
Secara garis besar sistem proyeksi peta bisa dikelompokkan berdasarkan pertimbangan
ekstrinsik dan intrinsik.
Pertimbangan Intrinsik
Berdasarkan sifat asli yang dipertahankan
Berdasarkan cara penurunan peta
Pertimbangan Ekstinsik
Berdasarkan sumbu proyeksi
Berdasarkan media proyeksi
Berdasarkan titik singgung dengan bidang proyeksi
Penjelasan yang lebih rinci akan dijelaskan dalam bagian selanjutnya.
10 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

11.
1.3 Sistem Proyeksi
1.3.1 Berdasarkan Sifat yang Dipertahankan
Hasil proyeksi peta yang baik harus bisa menyajikan luas, bentuk, arah (sudut),
dan jarak yang diproyeksikan dengan sekecil mungkin distorsi. Sementara bentuk
bumi sendiri akan membuat tak satupun sistem proyeksi yang bisa menghasilkan
peta dengan terpenuhinya persyaratan tersebut. Upaya mempertahankan salah
satu unsur berakibat terjadinya distorsi pada unsur yang lain. Maka dalam
melakukan proyeksi, biasanya ditentukan prioritas untuk mempertahankan unsur
tertentu saja, yaitu:
1.3.1.1 Proyeksi Ekuivalen
Pada proyeksi ini, luas daerah dipertahankan sama, artinya luas di atas
peta sama dengan luas di atas muka bumi setelah dikalikan skala.
1.3.1.2 Proyeksi Konform
Pada proyeksi ini, bentuk-bentuk dan arah sudut pada peta dipertahankan
agar sama dengan bentuk aslinya.
1.3.1.3 Proyeksi Ekuidistan
Pada proyeksi ini, jarak-jarak di peta sama dengan jarak di muka bumi
setelah dikalikan skala peta.
1.3.2 Berdasarkan Cara Penurunan Peta
1.3.2.1 Proyeksi Geometris
Disebut juga proyeksi perspektif atau proyeksi sentral.
1.3.2.2 Proyeksi Matematis
Hasil yang diperoleh dari proyeksi, diturunkan dalam peta dengan
perhitungan matematis.
1.3.2.3 Proyeksi Semi Geometris
Sebagian peta diperoleh dengan cara proyeksi dan sebagian lainnya
diperoleh dengan cara matematis.
11 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

12.
1.3.3 Berdasarkan Posisi Sumbu Proyeksi
1.3.3.1 Normal
Sumbu simetris bidang proyeksi berhimpit dengan sumbu bumi, atau
bidang proyeksinya menyinggung wilayah kutub.
Proyeksi normal
1.3.3.2 Transversal
Sumbu simetris bidang proyeksinya tegak lurus dengan sumbu bumi.
Disebut juga Proyeksi ekuatorial karena bidang proyeksi menyinggung
ekuator.
Proyeksi transversal
1.3.3.3 Oblique
Sumbu simetris bidang proyeksinya membentuk sudut terhadap sumbu
bumi. Digunakan untuk memetakan wilayah diantara kutub dan ekuator.
12 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

13.
Proyeksi Oblique
1.3.4 Berdasarkan Media Proyeksi
1.3.4.1 Azhimuthal
Proyeksi Azhimuthal berarti media proyeksinya berbentuk bidang datar.
Proyeksi Azimuthal.
Pada proyeksi Azhimuthal Normal, garis meridian (garis bujur) akan berupa
garis lurus yang berpusat di daerah kutub, sedangkan garis paralel (garis
lintang) berupa lingkaran-lingkaran konsentris yang mengelilingi kutub.
Proyeksi ini sangat cocok unutk menggambarkan wilayah di sekitar kutub.
13 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

14.
Contoh hasil proyeksi Azhimuthal. Sumber gambar: http://e-edukasi.net
Proyeksi Azhimuthal ini terbagi lagi menjadi tiga jenis berdasarkan pusat
proyeksinya, yaitu:
Gnomonik.
Pusat proyeksi ada di pusat bumi.
Stereografik.
Pusat proyeksi ada di kutub yang berlawanan dari titik singgung
bidang proyeksi.
Orthografik.
Pusat proyeksi berada di titik tak berhingga, sehingga garis
proyeksinya akan sejajar sumbu bumi.
Untuk lebih jelasnya, lihat gambar-gambar berikut.
14 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

15.
Proyeksi Azhimuthal normal dengan berbagai pusat proyeksi.
Sumber gambar: e-edukasi.net
1.3.4.2 Conical
Proyeksi Conical berarti bidang proyeksinya berbentuk kerucut. Proyeksi ini
sangat cocok untuk memetakan wilayah lintang tengah. Pada proyeksi
kerucut normal, garis paralel (garis lintang) akan berbentuk lengkungan,
sedangkan garis meridian (garis bujur) akan menyerupai jari-jari. Lihat
gambar berikut.
skema dasar proyeksi kerucut. Sumber gambar: http://e-edukasi.net
15 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

16.
Contoh hasil proyeksi kerucut. Sumber gambar: http://e-edukasi.net
1.3.4.3 Cylindrical
Media proyeksi pada proyeksi cylindrical berbentuk seperti slinder
(tabung).
Proyeksi Cylindrical. Sumber gambar: http://e-edukasi.net
Pada proyeksi slinder normal (berarti menyinggung khatulistiwa) maka
semua garis paralel (garis lintang) akan menjadi garis horisontal,
sedangkan semua garis meridian (garis bujur) akan menjadi garis vertikal.
Lihat gambar di bawah.
16 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

17.
Skema dasar proyeksi slinder dan contoh hasil proyeksinya.
sumber gambar: http://e-edukasi.net
Karena sifatnya pula, proyeksi slinder akan sangat baik untuk
menggambarkan daerah yang berada di dekat titik singgung bidang
proyeksi. Maka untuk proyeksi slinder normal, wilayah khatulistiwa akan
terproyeksikan dengan sangat baik, dan sebaliknya, wilayah kutub akan
terproyeksi dengan distorsi yang besar.
Ketiga jenis media proyeksi tersebut, secara ringkas dapat dilihat dalam tabel
berikut, dengan kombinasi kedudukan sumbu bidang proyeksinya terhadap sumbu
bumi.
17 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

18.
Normal Oblique Transversal
Azhimuthal
Conical
Cylindrical
Macam-macam proyeksi peta berdasarkan bidang proyeksi dan posisi sumbu
proyeksi terhadap sumbu bumi.
Sumber gambar: http://gd.itb.ac.id
1.3.5 Berdasarkan Titik Singgung dengan Bidang Proyeksi
1.3.5.1 Tangent
Proyeksi disebut tangent bila bidang proyeksinya menyinggung objek
proyeksinya, dalam hal ini bumi. Untuk Lebih jelasnya, lihat gambar
berikut:
18 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

19.
Proyeksi Tangent.. Sumber gambar: http://gd.itb.ac.id
1.3.5.2 Secant
Proyeksi bersifat secant bila bidang proyeksinya memotong objek
proyeksinya. Lihat gambar berikut:
Proyeksi Tangent.. Sumber gambar: http://gd.itb.ac.id
1.4 Proyeksi Gubahan (Arbitraty)
Proyeksi Gubahan berarti proyeksi yang didasarkan pada teknik proyeksi tertentu ditambah
beberapa kombinasi atau modifikasi, sesuai kebutuhan pemetaan. Sebagai contoh, proyeksi
Lambert Conformal Conical, berarti medianya berbentuk kerucut (conic), dengan sumbu
media proyeksinya berhimpit dengan sumbu bumi, serta mempertahankan bentuk-bentuk
atau sudut peta sesuai dengan aslinya (conformal).
Beberapa proyeksi gubahan yang terkenal akan dijelaskan berikut ini.
1.4.1 Berdasarkan Proyeksi Azimuthal
Proyeksi Azhimuthal, berarti media proyeksinya berupa bidang datar
1.4.1.1 Azimuthal Equidistant
Digunakan untuk peta skala besar dan biasa dipakai untuk menyajikan
lintasan penerbangan atau jalur komunikasi radio.
19 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

20.
Proyeksi Azimuthal Equidistant. Sumebr gambar: http://www.usgs.gov.
Hasil proyeksi . Sumebr gambar: http://www.colorado.edu
Ciri-ciri:
Jarak dan arah sudut di setiap tempat hanya benar jika diukur dari
titik pusat proyeksi
Jarak antar dua titik hanya benar sepanjang garis melewati titik
pusat
Distorsi bentuk dan luas semakin besar saat menjauhi titik pusat
20 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

21.
Garis lintang tergambar berupa lingkaran yang mengelilingi kutub.
1.4.1.2 Lambert Azimuthal Equal Area
Digunakan untuk daerah yang besarnya cenderung sama dari suatu titik
pusat, seperti benua Asia atau Samudera Pasifik. Diperkenalkan kali
pertama oleh Lambert pada tahun 1772.
Proyeksi Lambert Azimuthal Equal Area. Sumber gambar:
http://www.usgs.gov dan http://www.colorado.edu
Ciri-ciri:
Luas area secara proporsional akan sama dengan luas area di bumi
21 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

22.
Daerah persegi empat pada garis lintang yang sama memiliki luas
yang seragam
Arah sudut hanya benar dari titik pusat saja
Distorsi bentuk bertambah secara teratur saat menjauhi titik pusat
Semua garis lintang akan tergambar berupa lingkaran
Peta bersifat equal area, tapi bukan conformal, perspektif, atau
equidistant.
1.4.1.3 Orthographic
Digunakan untuk melihat secara perspektif bentuk bumi, bulan, atau
bentuk benda langit lainnya. Sudah dikenal sejak 2.000 tahun silam di
tengah kebudayaan Mesir dan Yunani.
22 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

23.
Proyeksi Orthografik. Sumber gambar: http://www.usgs.gov dan
http://www.colorado.edu
Ciri-ciri:
Arah sudut hanya benar dari titik pusat saja
Skala akan mengecil saat menjauh dari titik pusat lingkaran
Semua garis lintang akan tergambar berupa lingkaran
Distorsi bentuk dan luas bertambah semakin jauh dari titik pusat
Peta bersifat perspektif, namun bukan conformal atau equal area
23 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

24.
1.4.1.4 Stereographic
Digunakan untuk memetakan daerah atau benua yang luas dengan bentuk
yang relatif serupa di segala arah. Juga digunakan untuk peta topografi
bagi keperluan navigasi di kawasan di atas garis lintang 80o LU. Sudah
dikenal sejak abad ke-2 SM seperti dituturkan oleh Hipparchus.
Proyeksi Sereographic. Sumber gambar: http://www.usgs.gov dan
http://www. colorado.edu
Ciri:
Arah sudut hanya benar dari titik pusat proyeksi
Skala bertambah saat semakin jauh dari titik pusat
Distorsi bentuk dan luas bertambah saat menjauh dari titik pusat
24 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

25.
Peta bersifat konfrm dan perspektif, namun tidak equal area atau
ekuidistan.
1.4.2 Berdasarkan Proyeksi Kerucut (Conical)
Proyeksi ini menggunakan kerucut sebagai bidang media proyeksinya
1.4.2.1 Proyeksi Albers Equal Area Conic
Digunakan Diguankan untuk memetakan daerah yang orientasinya Timur-
Barat dan membutuhkan penyajian equal area. Banyak dugunakan untuk
peta tematik. Peta-peta yang dihasilkan bisa digabungkan hanya jika
memiliki standar paralel yang sama dengan skala yang sama pula.
Diperkenalkan kali pertama oleh HC Albers pada tahun 1805.
Skema proyeksi Albers Equal Area Conic. Sumber gambar:
http://www.usgs.gov
Ciri-ciri:
Semua luas di peta secara proporsional sama dengan luas di bumi.
Arah sudut hanya benar di wilayah terbatas
Jarak di peta hanya benar pada kedua garis standar paralel
Peta tidak bersifat conformal, perspektif, ataupun equidistant
25 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

26.
1.4.2.2 Equidistant Conic
Proyeksi ini, seperti halnya proyeksi kerucut lainnya, digunakan untuk
memetakan wilayah lintang tengah (middle latitudes) atau wilayah antara
khatulistiwa dan kutub. Digunakan untuk memetakan daerah lintang
tengah, antara khatulistiwa dan kutub. Prototipe pertamanya dibuat oleh
Ptolemy pada tahun 150 yang kemudian dikembangkan oleh De I'lsle
sekitar tahun 1745.
Proyeksi Equidistant Conic. Sumber gambar: http://www.usgs.gov
Ciri-ciri:
Jarak di peta hanya benar sepanjang meridian serta satu atau dua
garis standar paralel
Arah sudut, bentuk, dan luas cukup akurat, meskipun distorsi akan
bertambah saat menjauhi standar paralel
Peta tidak bersifat conformal, perspektif, ataupun equal area.
Merupakan kompromi antara Lambert Conformal Conic dan Albers
Equal Conic.
1.4.2.3 Lambert Conformal Conic
Seperti proyeksi kerucut lainnya, proyeksi ini juga biasanya digunakan di
area antara khatulistiwa dan kutub dengan orientasi Barat-Timur. Peta-
peta yang dibuat menggunakan sistem proyeksi Lambert ini, saat ini
banyak digunakan secara luas di Amerika Serikat. Proyeksi ini sebenarnya
26 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

27.
mirip seperti proyeksi Albers Equal Area Conic, namun ada perbedaan pada
hasil spasi antar garisnya. Diperkenalkan pertama kali oleh pak Lambert
pada tahun 1772.
Proyeksi Lambert Conformal Conic. Sumber gambar: http://www.usgs.gov
dan http://www.kartoweb.itc.nl
Ciri-ciri:
Jarak pada peta hanya benar sepanjang garis standar paralel
Arah sudut peta akurat
27 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

28.
Distorsi bentuk dan luas tidak besar, namun bertambah saat
menjauhi standar paralel
Baik pada peta skala kecil maupun besar, bentuk yang dihasilkan
tidak akan berbeda
Peta bersifat conformal tapi tidak perspektif, equal area, maupun
equidistant.
1.4.2.4 Polyconic
Digunakan untuk memetakan daerah dengan orientasi Utara-Selatan.
Banyak digunakan pada masa-masa awal peta USGS. Meridian tengah
berupa garis lurus, meridian lainnya berupa kurva dengan bentuk
kompleks. Konsepnya diperkenalkan kali pertama oleh pak Hassler pada
tahun 1820.
Proyeksi Polyconic. Sumber gambar: http://www.usgs.gov
28 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

29.
Proyeksi Polyconic. Sumber gambar: http://www.colorado.net
Ciri-ciri:
Arah sudut pada peta hanya benar pada sepanjang meridian
tengah
Jarak pada peta hanya benar pada meridian tengah dan garis
paralel
Bentuk dan luas hanya benar di sekitar meridian tengah
Distorsi semakin bertambah saat menjauhi meridian pusat
Peta tidak bersifat konformal, perspektif, maupun equal area
Merupakan kompromi dari berbagai teknik proyeksi.
1.4.3 Berdasarkan Proyeksi Slinder
1.4.3.1 Mercator
Proyeksi Mercator, kali pertama dikenalkan oleh Gerardus Mercator (1512-
1594). Merupakan proyeksi silinder normal conform (berarti: bidang
proyeksinya berbentuk slinder, sumbu bidang proyeksinya berimpit dengan
29 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

30.
sumbu bumi, dan mempertahankan sudut-sudut atau arah peta sesuai
aslinya).
Proyeksi Mercator akan menghasilkan peta yang
sangat representative di wilayah ekuator, namun
menghasilkan distorsi yang besar di wilayah
kutub bahkan tak bisa dipetakan karena kutub
akan berada di titik tak berhingga. Karena itu,
proyeksi mercator tidak memetakan wilayah
kutub. Peta hasil proyeksi Mercator sering
digunakan di bidang maritim, sebab garis-garis
hasil pemetaannya memiliki azimuth yang
konstan (arah garis sesuai dengan garis lintang
dan bujur). Lihat gambar di bawah ini,
Proyeksi Mercator. Sumber gambar: http://www.usgs.gov
1.4.3.2 Transverse Mercator
Dilihat dari namanya, bisa disimpulkan bahwa proyeksi ini sama dengan
proyeksi Mercator tetapi dengan sumbu yang tegak lurus dengan sumbu
bumi. Proyeksi ini digunakan secara luas di dunia dalam berbagai skala.
Peta-peta yang dihasilkan bisa digabungkan jika hanya berada pada zona
yang sama dengan satu meridian tengah. Meskipun proyeksi Mercator
diperkenalkan kali pertama oleh Gerardus Mercator pada tahun 1569,
namun proyeksi Transverse Mercator dikembangkan oleh pak Lambert
pada tahun 1772. Lihat gambar berikut,
30 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

31.
Proyeksi Transverse Mercator. Sumber gambar: http://www.usgs.gov
Ciri-ciri:
Jarak pada peta hanya benar sepanjang meridian tengah yang
dipilih/ditentukan oleh pembuat peta, atau selama berada diantara
dua garis paralel
Secara umum, semua jarak di peta, arah sudut, bentuk, dan luas
di peta hanya akurat dalam jarak sejauh 15o dari meridian pusat
Distorsi jarak, arah sudut, bentuk, dan luas akan meningkat secara
cepat di luar pita 15o tersebut
Garis meridian pusat dan tiap meridian yang jaraknya 90o dari
meridian pusat akan berupa garis lurus.
1.4.3.3 Universal Transverse Mercator
Sebenarnya istilah UTM lebih mengacu kepada suatu system grid dan
penomoran. Sebab pada dasarnya, UTM merupakan Proyeksi Transverse
Mercator dengan beberapa ketentuan tambahan, yaitu:
Merupakan sistem proyeksi cylindrical, conformal, secant, dan
transversal
31 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

32.
Proyeksi UTM serta perpotongan slinder degan meridian. Sumber gambar:
http://manifold.net
Bidang silinder memotong bola bumi pada dua meridian yang
disebut meridian standar dengan faktor skala 1
Lebar tiap zone 6° dan memiliki meridian tengah sendiri
Tinggi tiap zone adalah 8°. Batas paralel tepi atas dan tepi bawah
adalah 84° LU dan 80° LS
Perbesaran di meridian tengah = 0.9996 (mendekati 1, karena
bidang berimpit dengan bumi.
32 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

33.
Gambar zona ke-48 pada system grid UTM. Sumber gambar:
http://www.colorado.edu
Proyeksi Universal Transverse Mercator (UTM) digunakan untuk
mendefinisikan posisi seluruh dunia dengan membaginya menjadi area
atau zona 6°. Masing-masing zona ini diproyeksikan dengan menggunakan
proyeksi mercator. Dengan meridian pusat sebagai pusat zona. Sedangkan
arah vertikalnya, UTM hanya memetakan area antara 80° LU dan 84° LU.
Dengan demikian, zona UTM dibagi menjadi 60 zona horizontal x 20 zona
vertical. Sistem penomoran diatur sebagai berikut:
Untuk zona horizontal, ditandai dengan angka 1 sampai dengan
60. Dimulai dari 180° BB hingga 180° BT.
Untuk zona vertical, ditandai dengan huruf dimulai dari C hingga X
dengan menghilangkan huruf I dan O.
33 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

34.
Aturan ini sering membuat UTM disebut sebagai system Northing-Easting,
karena system penomoranya bergerak ke arah utara dan ke arah timur.
34 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

35.
35 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

36.
1.4.3.4 Oblique Mercator
Proyeksi ini diprioritaskan untuk memetakan daerah di luar khatulistiwa
ataupun kutub, dan dikenal sebagai wilayah "Great Circle". Diperkenalkan
kali pertama oleh Rosenmund, Laborde, Hotine dkk pada masa 1900—
1950.
Proyeksi Oblique Mercator. Sumber gambar: http://www.usgs.gov
Ciri-ciri:
Jarak di peta hanya benar sepanjang "Great Circle" atau sepanjang
garis singgung proyeksi dengan bumi
Semua jarak, arah sudut, bentuk, dan luas di peta hanya akurat
dalam jarak sejauh 15o dari meridian pusat
Distorsi jarak, arah sudut, bentuk, dan luas secara cepat akan
meningkat di luar pita 15o tersebut
Digunakan untuk memetakan area berbentuk panjang dengan arah
Utara - Selatan dan jauh dari ekuator, misalnya Cili atau Alaska.
36 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

37.
Proyeksi Alaska State Plane Zone 5001. Sumber gambar:
http://www.kartoweb.itc.nl
1.4.3.5 Space Oblique Mercator
Proyeksi ini dirancang untuk menunjukkan gambar hasil pencitraan
lengkungan bumi oleh satelit Landsat. Ada sedikit distorsi sepanjang hasil
penjejakan satelit, namun hanya dalam pita sempit, yaitu sekitar 15o.
Dikembangkan kali pertamanya oleh by AP. Colvocoresses, JP. Snyder, and
JL. Junkins pada tahun 1973–79.
Proyeksi Space Oblique Mercator. Sumber gambar: http://www.usgs.gov
37 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

38.
Proyeksi Space Oblique Mercator. Sumber gambar:
http://www.colorado.edu
1.4.3.6 Cylindrical Equal Area
Proyeksi ini menghasilkan garis Lintang dan Bujur yang lurus dengan spasi
antar garis lintang yang seragam namun spasi antara garis bujur tidak
sama. Bisa dibagi menjadi Normal, Transversal, serta Oblique, sesuai
dengan posisi sumbu proyeksinya. Peta yang dihasilkan akan memiliki
skala yang benar pada garis tengah. Karena sifatnya pula, distorsi akan
terjadi sesuai dengan bertambahnya jarak dari garis tengah peta.
Beberapa jenis proyeksi ini antara lain:
Behrmann Cylindrical Equal-Area
Proyeksi ini menggunakan garis lintang 30o sebagai garis paralel
yang bebas distorsi. Itu artinya, garis lintang 30o menjadi daerah
"irisan" antara model bumi dan tabung proyeksi.
38 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

39.
Proyeksi Behrman's Cylindrical Equal Area. Sumber gambar:
http://www.colorado.edu
Gall's Stereographic Cylindrical
Proyeksi ini merupakan hasil dari proyeksi permukaan bumi dari
wilayah khatulistiwa pada media tabung (slinder) dengan metoda
secant yang memotong bola bumi pada garis 45o LS dan 45o LU.
Distorsi akan terjadi pada jarak, bentuk, dan luas area.
1.4.3.7 Miller Cylindrical
Digunakan untuk memetakan seluruh bumi dalam suatu bingkai persegi
panjang. Proyeksi ini menghasilkan peta dengan garis Lintang dan Bujur
yang lurus. Tapi garis-garis ini tidak memiliki Azimuth yang konstan.
Sekilas mirip hasil proyeksi Mercator, namun peta yang dihasilkan tidak
bisa digunakan untuk navigasi. Diperkenalkan kali pertama oleh OM. Miller
pada tahun 1942.
Beberapa ciri proyeksi ini antara lain:
Arah sudut peta, dan jarak di peta hanya benar sepanjang
khatulistiwa.
Distorsi jarak, luas, dan bentuk akan meningkat secara tajam pada
wilayah lintang "tinggi"
Daerah kutub digambarkan dalam bentuk lurus
39 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

40.
Peta tidak bersifat equal area, ekuidistan, konform, atau
perspektif.
Proyeksi Miller Cylindrical. Sumber gambar: http://www.usgs.gov
1.4.4 Proyeksi Pseudocylindrical (Slinder Semu)
Proyeksi ini dibangun berdasarkan proyeksi slinder dengan pengaturan tambahan,
yaitu:
Garis-garis lintang (latitude) digambarkan sebagai garis lurus paralel
Garis-garis bujur digambarkan sebagai garis kurva (kecuali meridian
tengah yang berupa garis lurus) dengan spasi antar garis bujur yang
seragam jaraknya.
Beberapa proyeksi Pseudocylindrical akan dijelaskan di bawah ini.
1.4.4.1 Proyeksi Mollweide
Proyeksi Mollweide digunakan untuk membuat peta-peta dunia secara
global. Merupakan proyeksi pseudocylindrical dan equal area. Garis Bujur
Pusat (central meridian) diproyeksikan lurus, sedang garis meridian ke-90
menjadi lengkungan lingkaran.
40 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

41.
Proyeksi Mollweide Equal Area. Sumber gambar:
http://www.kartoweb.itc.nl
1.4.4.2 Proyeksi Sinusoidal Equal Area
Biasanya digunakan untuk membuat peta menyajikan pola penyebaran
parameter tertentu. Bisa memiliki satu meridian tengah atau lebih.
Diperkenalkan kali pertama oleh Cossin-Honduins sejak tahun 1570 serta
Sanson-Flamsteed.
Ciri-ciri:
Luas di peta secara proporsional sama dengan di bumi
Jarak di peta hanya benar sepanjang semua garis paralel dan
meridian tengah
Distorsi bentuk di peta akan meningkat saat menjauhi meridian
tengah dan di dekat kutub
Peta tidak bersifat konformal, perspektif, atau equidistant.
41 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

42.
Proyeksi Sinusoidal. Sumber gambar: http://www.colorado.edu
1.4.4.3 Proyeksi Robinson
Diperkenalkan kali pertama oleh Arthur H. Robinson pada 1963. Proyeksi
ini menggunakan tabel koordinat dalam pembuatannya dan bukannya
rumus matematika, sehingga dunia yang dipetakan seolah-olah benar. Tapi
peta ini mengandung distorsi (cacat) dalam hal bentuk, luas, skala, serta
jarak pada peta yang dihasilkan. Peta-peta dunia dari National Geographic
banyak menggunakan proyeksi ini.
Ciri-ciri:
Sudut peta memiliki arah yang benar di semua garis paralel dan
sepanjang garis meridian pusat.
Jarak yang konstan sepanjang khatulistiwa dan garis lintang
lainnya, tapi dengan skala yang variatif
Skala yang benar dalam area antara 38o LS dan 38o LU, dan
konstan sepanjang berada dalam garis lintang yang sama
Distorsi yang besar akan terjadi di wilayah kutub.
Peta tidak bersifat konformal, equal area, ekuidistan, ataupun
perspektif.
42 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

43.
Proyeksi Robinson. Sumber gambar: http://www.kartoweb.itc.nl
Masih ada beberapa proyeksi Pseudocylindrical yang lain, namun tidak akan
dibahas di sini, seperti proyeksi Eckert yang terbagi menjadi Eckert IV Equal Area
dan Eckert VI Equal Area.
1.5 Penggunaan Proyeksi
Dengan beragamnya jenis proyeksi ini, maka banyak pula pilihan bagi pembuat peta.
Masing-masing proyeksi ini punya kelebihan sesuai dengan sifatnya, dan hanya cocok bila
digunakan untuk memetakan wilayah tertentu. Artikel yang terdapat di http://manifold.net
memberi rekomendasi sebagai berikut:
Area yang akan Dipetakan Proyeksi yang Dianjurkan
Gunakan proyeksi Robinson atau Miller Cylindrical.
Seluruh Dunia
Proyeksi Robinson cukup sesuai untuk peta tematik.
- Untuk wulayah Amerika Utara dan Eurasia,
gunakan proyeksi Lambert Conformal Conical.
- Untuk wilayah Amerika Selatan dan Afrika,
Benua gunakan Lambert Azimuthal Equal Area atau
Ortografik.
- Untuk wilayah Australia dan Antartika,
gunakan Ortografik.
43 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

44.
- Untuk wilayah semacam Amerika Serikat, Kanada,
Rusia,
atau RRCina, gunakan Lambert Conformal Conic.
Daerah dengan orientasi - Untuk wilayah Eropa, baik Lambert Conformal Conic
Timur - Barat atau Ortografik bisa digunakan.
- Untuk wilayah lain yang daerahnya berorientasi
Timur - Berat, gunakan Ortografik
atau Lambert Azimuthal Equal Area
Kutub Ortografik atau Lambert Azimuthal Equal Area
Samudera Ortografik atau Lambert Azimuthal Equal Area
Negara / Daerah Kecil Ortografik
Daerah yang panjang, sempit, dan arahnya utara selatan
Daerah dengan orientasi seperti negara Cili, sangat cocok menggunakan proyeksi
Utara - Selatan Transvere Mercator. Daerah "oblique" seperti alaska,
biasanya dipetakan dengan proyeksi Oblique Mercator
44 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM

45.
Maraji'
Buku
1. Sandy, I Made, Esensi Kartografi, Jurusan Geografi FMIPA UI, Jakarta, 1987.
2. Prihandito, A., Proyeksi Peta, Kanisius, Yogyakarta, 1988.
3. Prijatna, Kosasih., Proyeksi Peta - Hand Out Kuliah, Fakultas Teknik Geodesi ITB,
Bandung, 2005.
4. Sutama, Drs., Skala Dan Proyeksi - Modul Ajar SMA No. Geo.I.03, tanpa tempat
terbit, tanpa tahun terbit.
5. Sosrodarsono, S. dan Takasaki, M. (Editor), Pengukuran Topografi dan Teknik
Pemetaan, PT Pradnya Paramita, Jakarta, 1983.
Situs
6. http://www.geodesi.info
7. http://www.colorado.edu
8. http://www.kartoweb.itc.nl
9. http://www.geomatika.its.ac.id
10. http://www.e-edukasi.net
11. http://agussupriyanto.blogspot.com
*Anggota ASTACALA, Perhimpunan Mahasiswa Pencinta Alam ITTelkom
Copyright : Diperbolehkan mengutip keseluruhan atau sebahagian dari isi dokumen ini
dengan atau tanpa ijin penulis dengan tetap menyajikan kredit penulis.
45 SISTEM PROYEKSI PETA | ASTACALA PMPA ITTELKOM