FM-indexによる全文検索

FM-Indexによる全文検索
計算機実習E 自由課題

• 文書から文字列を検索する方法は2通りに分類できる
A. 前処理が不要な方法 (力任せな方法, KMP法, BM法)
B. 前処理が必要な方法 (転置インデックス, 接尾辞配列)
• Bは前処理の時間が必要なかわりに, 
同じ文書から何回も検索する場合はAよりも高速
• FM-IndexはBに分類される方法で, 
文書の長さに依存しない時間で検索できる

前処理１：接尾辞配列の構築
文書
mississippi
mississippi$
エンドマーカ$を追加
mississippi$
ississippi$
ssissippi$
sissippi$
issippi$
ssippi$
sippi$
ippi$
ppi$
pi$
i$
$
接尾辞の列挙

前処理１：接尾辞配列の構築
0 mississippi$
1 ississippi$
2 ssissippi$
3 sissippi$
4 issippi$
5 ssippi$
6 sippi$
7 ippi$
8 ppi$
9 pi$
10 i$
11 $
11 $
10 i$
7 ippi$
4 issippi$
1 ississippi$
0 mississippi$
9 pi$
8 ppi$
6 sippi$
3 sissippi$
5 ssippi$
2 ssissippi$
辞書順でソートする
※$は任意のアルファベットよりも 
順位が小さいとする
接尾辞配列SA

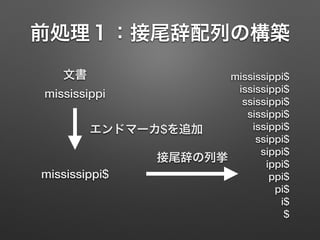
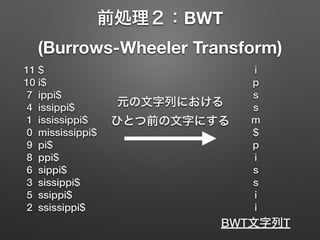
前処理２：BWT 
(Burrows-Wheeler Transform)
11 $
10 i$
7 ippi$
4 issippi$
1 ississippi$
0 mississippi$
9 pi$
8 ppi$
6 sippi$
3 sissippi$
5 ssippi$
2 ssissippi$
元の文字列における 
ひとつ前の文字にする
i
p
s
s
m
$
p
i
s
s
i
i
BWT文字列T

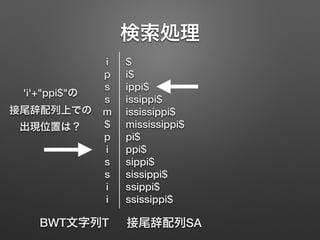
検索処理
• BWT文字列T = ipssm$pissii について, 
次の関数を定義する
• Rank(c,p) : T[0,p)の範囲で, 
アルファベットcの出現数を返す
• RankLT(c) : T全体で, cよりも順位が小さい 
アルファベットの出現数を返す

検索処理
$
i$
ippi$
issippi$
ississippi$
mississippi$
pi$
ppi$
sippi$
sissippi$
ssippi$
ssissippi$
i
p
s
s
m
$
p
i
s
s
i
i
BWT文字列T 接尾辞配列SA

検索処理
$
i$
ippi$
issippi$
ississippi$
mississippi$
pi$
ppi$
sippi$
sissippi$
ssippi$
ssissippi$
i
p
s
s
m
$
p
i
s
s
i
i
'i'+"ppi$"の 
接尾辞配列上での 
出現位置は？

検索処理
$
i$
ippi$
issippi$
ississippi$
mississippi$
pi$
ppi$
sippi$
sissippi$
ssippi$
ssissippi$
i
p
s
s
m
$
p
i
s
s
i
i
'i'+"ppi$"の 
接尾辞配列上での 
出現位置は？
LF-mapping
c=T[p] に続く文字列の 
SA上での出現位置は 
RankLT(c)+Rank(c,p)

検索処理
$
i$
ippi$
issippi$
ississippi$
mississippi$
pi$
ppi$
sippi$
sissippi$
ssippi$
ssissippi$
i
p
s
s
m
$
p
i
s
s
i
i
"ssi"の検索
[RankLT('i')+Rank('i', 0), 
RankLT('i')+Rank('i', 12))
'i'で始まる 
文字列

検索処理
$
i$
ippi$
issippi$
ississippi$
mississippi$
pi$
ppi$
sippi$
sissippi$
ssippi$
ssissippi$
i
p
s
s
m
$
p
i
s
s
i
i
"ssi"の検索
[RankLT('s')+Rank('s', 1), 
RankLT('s')+Rank('s', 5))
's'+"i"で始まる 
文字列

検索処理
$
i$
ippi$
issippi$
ississippi$
mississippi$
pi$
ppi$
sippi$
sissippi$
ssippi$
ssissippi$
i
p
s
s
m
$
p
i
s
s
i
i
"ssi"の検索
[RankLT('s')+Rank('s', 8), 
RankLT('s')+Rank('s', 10))
's'+"si"で始まる 
文字列

検索処理
• FM-indexは, 検索文字列に対応する位置の絞り込みを 
LF-mappingの繰り返しによって行う
• LF-mappingは Rank と RankLT で行える
• この2つの処理は, ウェーブレット木やウェーブレット行列を使えば 
O(log σ) 時間で可能 (σ はアルファベットの種類数)
• LF-mappingを検索文字列Qの長さ分だけ繰り返すので, 
一回の検索がO(m log σ) 時間で可能 (m は Q の文字数)
• 検索時間が文書の長さに依存しない

制作物
• 青空文庫で人気がある図書500冊を対象とした 
ウェブブラウザから使えるインクリメンタル検索を制作
• 接尾辞配列の構築はsais.hxx (高速なライブラリ) を使用
• ウェーブレット行列とFM-Indexは自分で実装 (C++), 
boost-pythonによりPython用の拡張モジュールに変換
• Flask (Web App Framework@Python) から呼び出す

うまくいかなかったところ
• あいまい検索を実装しようとして文献を探してみた 
→ 編集距離に対して指数時間かかるらしい…
• 作成した索引をファイルから読み込む処理で, 
既存のライブラリを使ったら使用メモリの量が爆発 
(原因不明)

まとめ
• 高速な文字列検索のアルゴリズムを実装してみた
• ブラウザから使えるようにしてみた
!
• 参考文献
• 岡野原大輔. 高速文字列解析の世界. 岩波書店. 2012.

(補足) ウェーブレット木
3101212213
1000101101
10111 32223
10111 10001
下位2ビット目 →
下位1ビット目 →
0 1111 222 33
0 1
0 1 0 1

FM-indexによる全文検索

More Related Content

What's hot

Similar to FM-indexによる全文検索

More from Sho IIZUKA

FM-indexによる全文検索