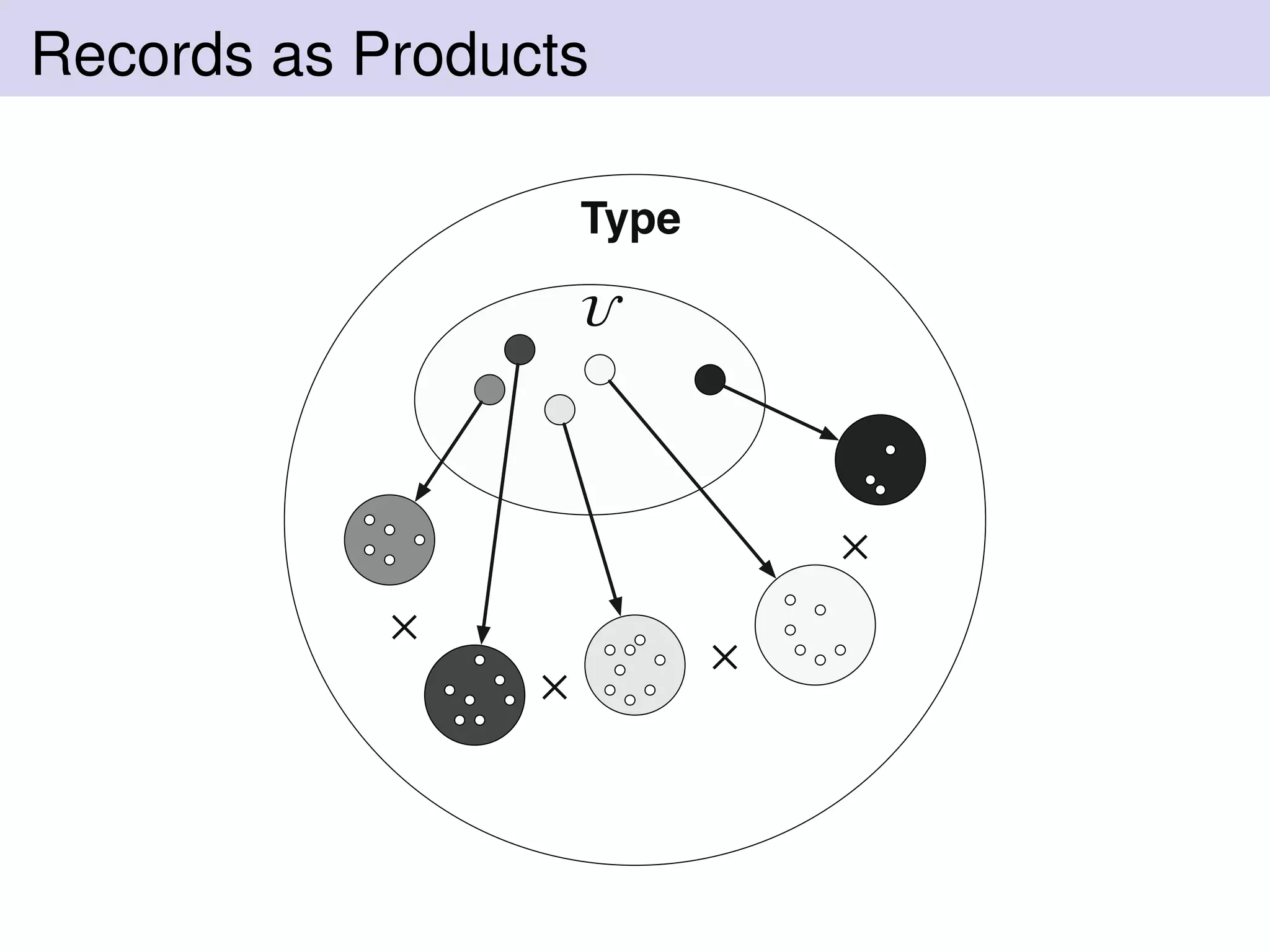
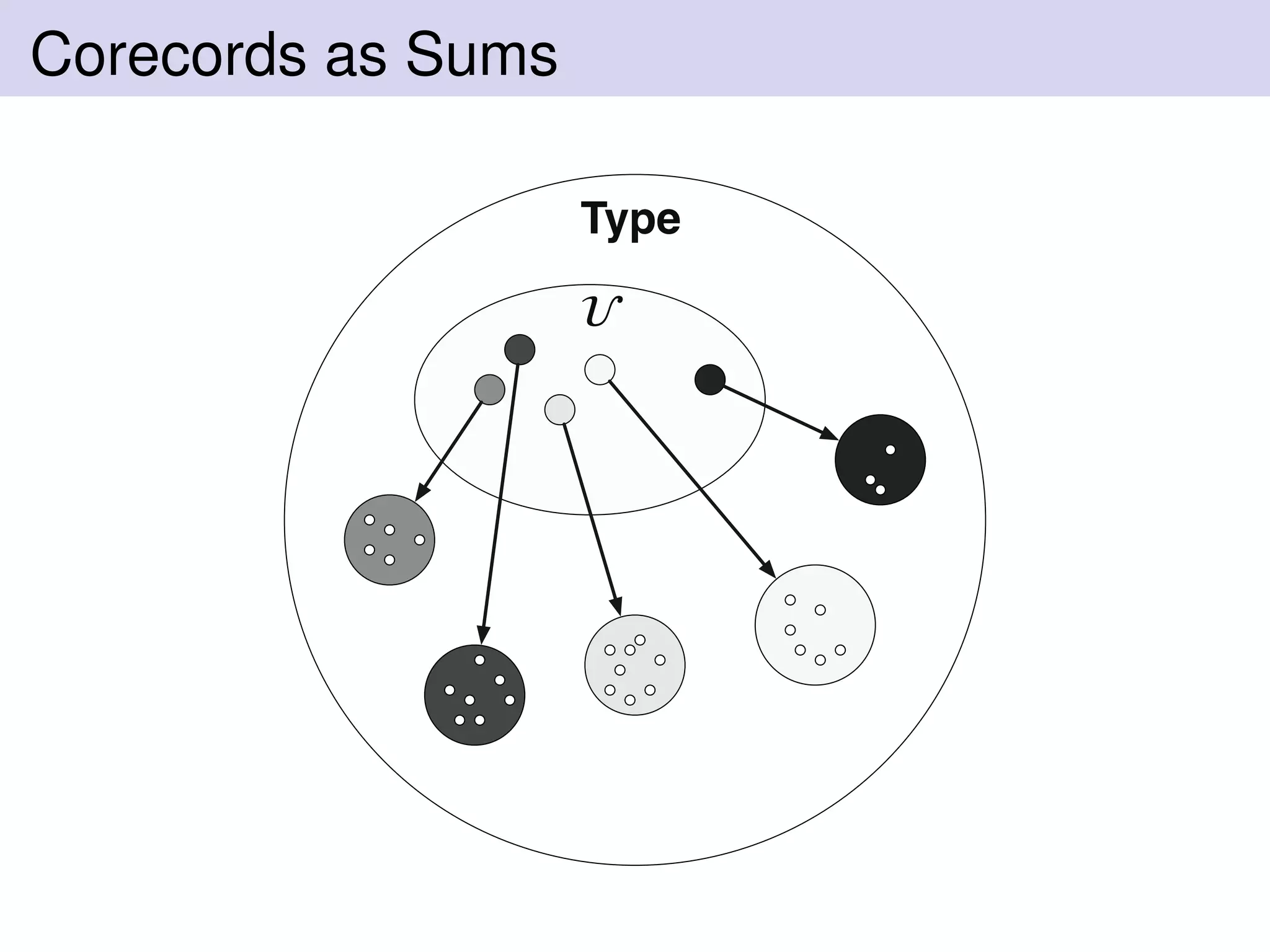
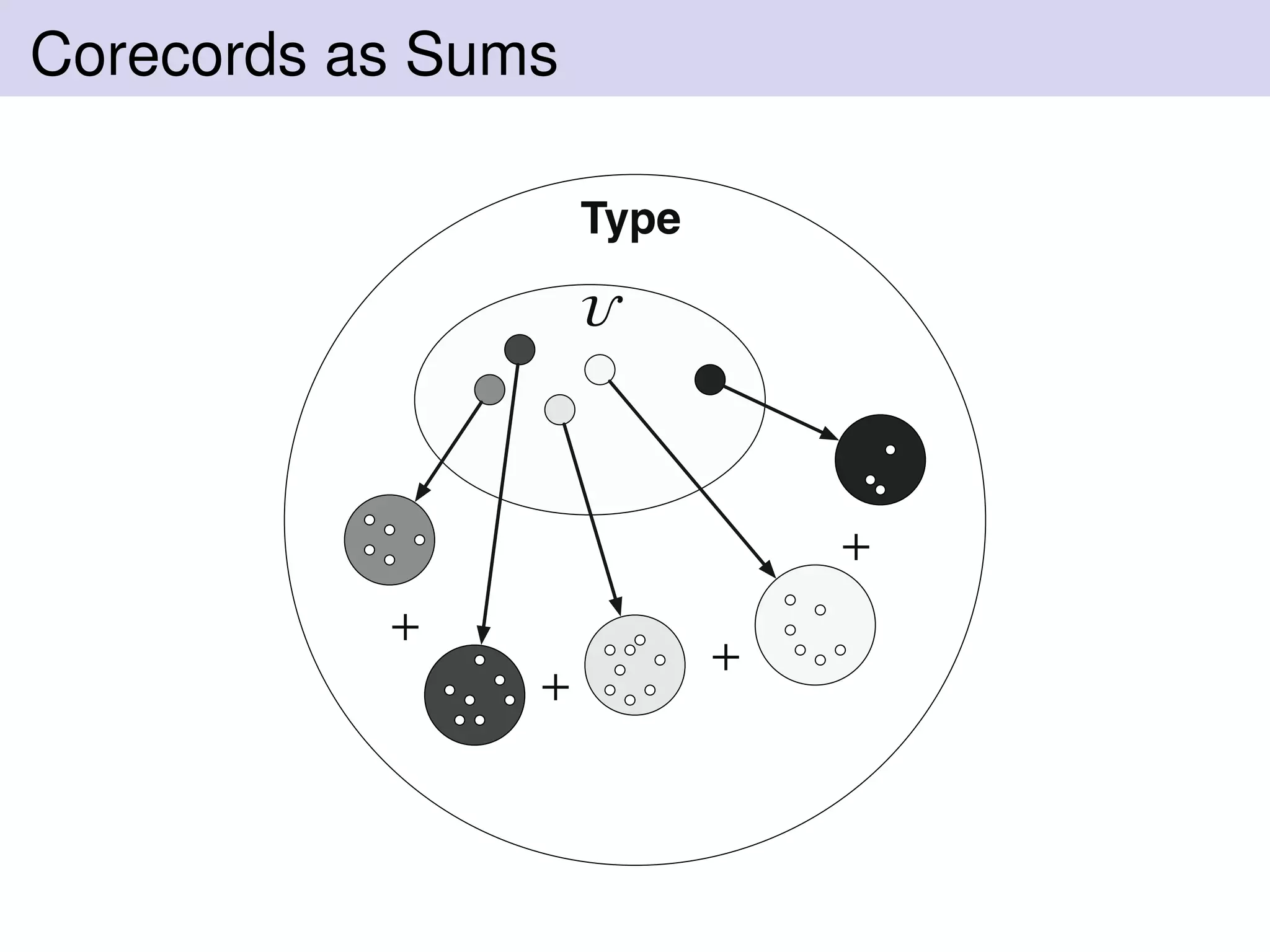
The document discusses records and row polymorphism in Haskell. It begins by explaining that Haskell records are nominally typed and cannot share field names. It then discusses structural typing and row polymorphism as ways to address these limitations. The document proposes modeling records as products in a universe, and corecords as sums. It shows how to implement records and row polymorphism in Haskell using type families, and how this recovers HLists. The document also discusses validating records, effects inside records, and modeling records as presheaves.















![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-16-2048.jpg)
![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where
RNil :: Rec ’[]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-17-2048.jpg)
![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where
RNil :: Rec ’[]
(:&) :: !t → !(Rec rs) → Rec ((s ::: t) ’: rs)](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-18-2048.jpg)
![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where
RNil :: Rec ’[]
(:&) :: !t → !(Rec rs) → Rec ((s ::: t) ’: rs)
class s ∈ (rs :: [∗])](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-19-2048.jpg)
![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where
RNil :: Rec ’[]
(:&) :: !t → !(Rec rs) → Rec ((s ::: t) ’: rs)
class s ∈ (rs :: [∗])
class ss ⊆ (rs :: [∗]) where
cast :: Rec rs → Rec ss](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-20-2048.jpg)
![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where
RNil :: Rec ’[]
(:&) :: !t → !(Rec rs) → Rec ((s ::: t) ’: rs)
class s ∈ (rs :: [∗])
class ss ⊆ (rs :: [∗]) where
cast :: Rec rs → Rec ss
(=:) : s ::: t → t → Rec ’[s ::: t]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-21-2048.jpg)
![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where
RNil :: Rec ’[]
(:&) :: !t → !(Rec rs) → Rec ((s ::: t) ’: rs)
class s ∈ (rs :: [∗])
class ss ⊆ (rs :: [∗]) where
cast :: Rec rs → Rec ss
(=:) : s ::: t → t → Rec ’[s ::: t]
(⊕) : Rec ss → Rec ts → Rec (ss ++ ts)](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-22-2048.jpg)
![Roll Your Own in Haskell
data (s :: Symbol) ::: (t :: ∗) = Field
data Rec :: [∗] → ∗ where
RNil :: Rec ’[]
(:&) :: !t → !(Rec rs) → Rec ((s ::: t) ’: rs)
class s ∈ (rs :: [∗])
class ss ⊆ (rs :: [∗]) where
cast :: Rec rs → Rec ss
(=:) : s ::: t → t → Rec ’[s ::: t]
(⊕) : Rec ss → Rec ts → Rec (ss ++ ts)
lens : s ::: t ∈ rs ⇒ s ::: t → Lens’ (Rec rs) t](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-23-2048.jpg)






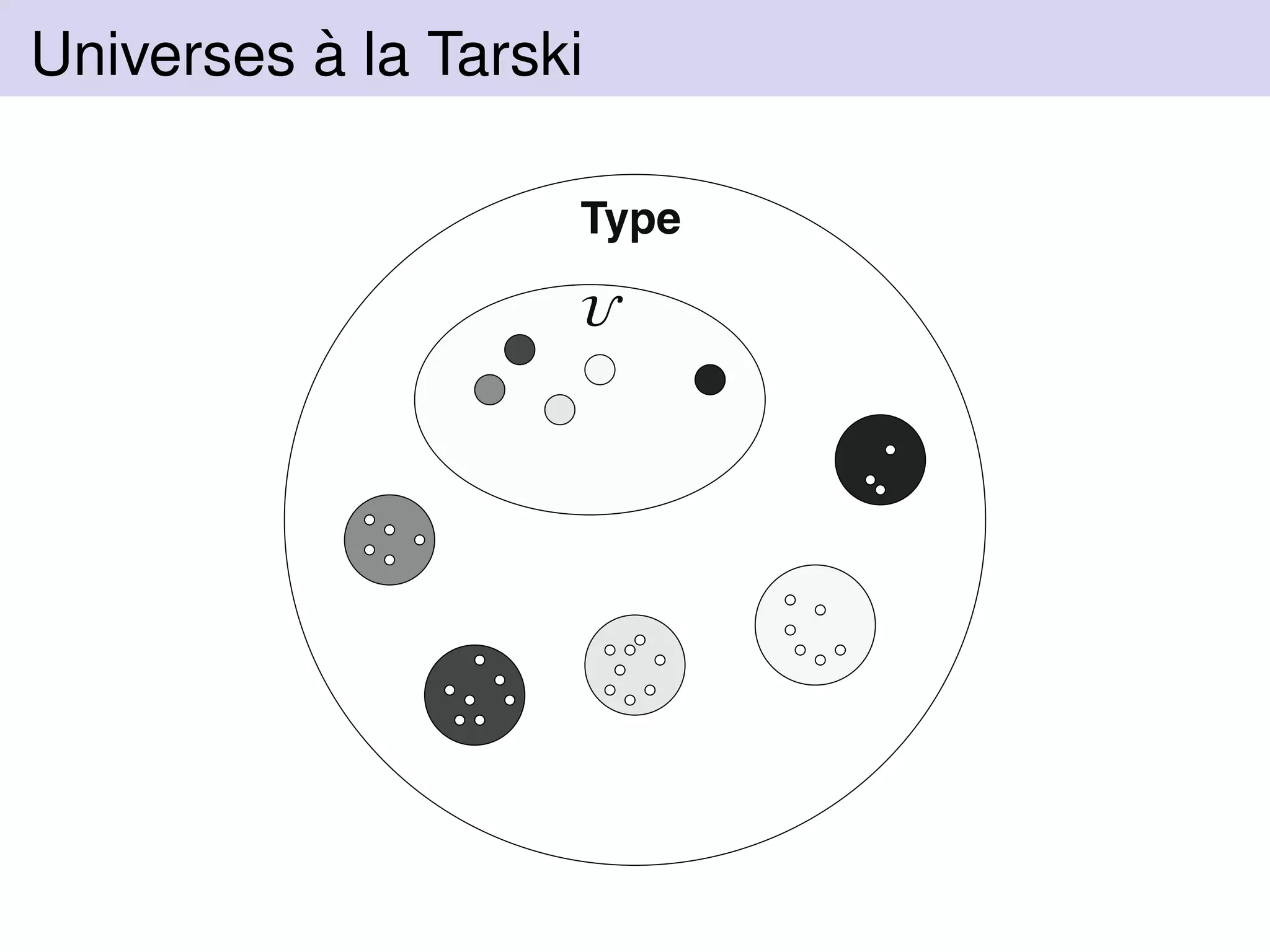
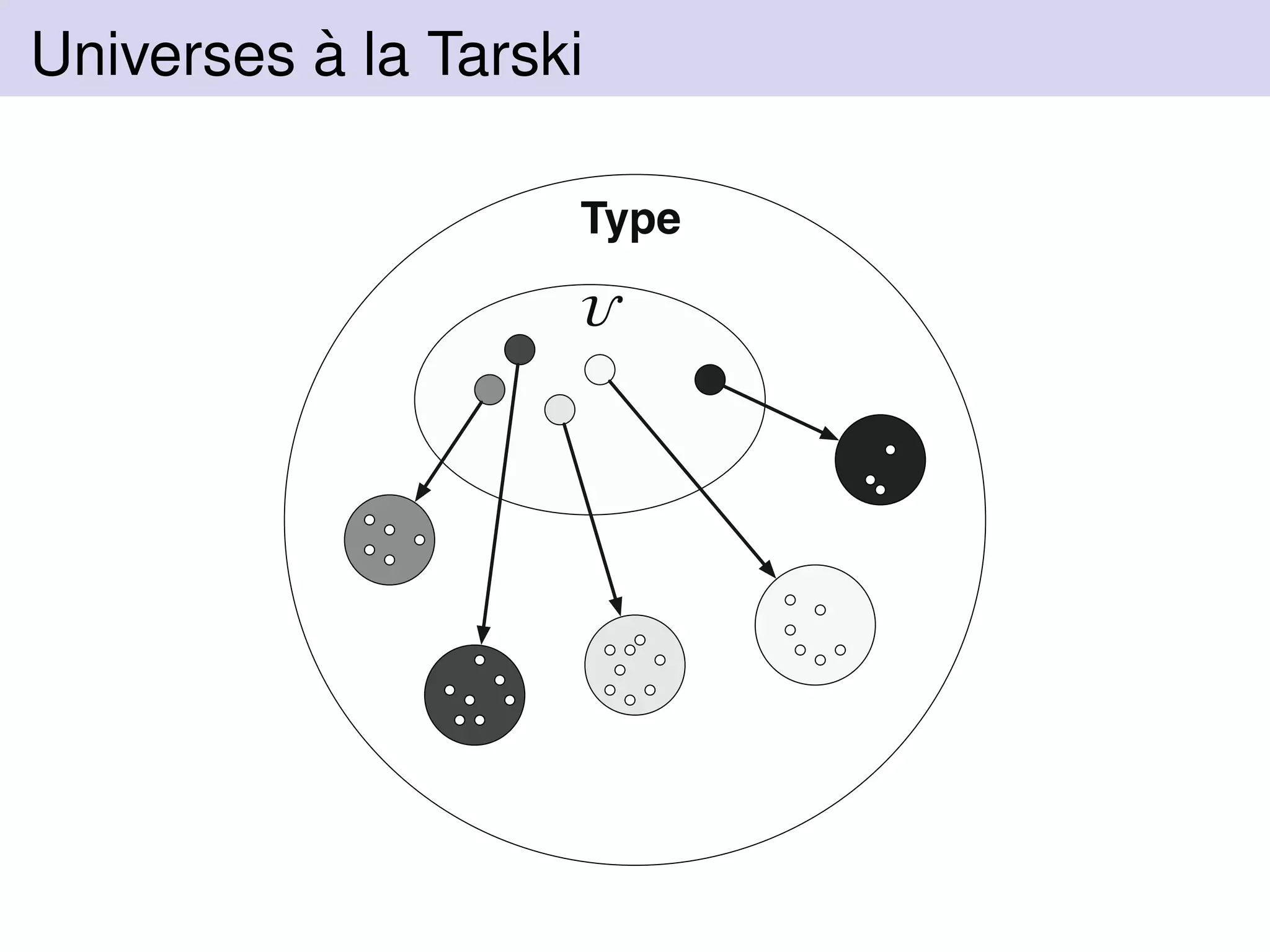





![A Closed Universe
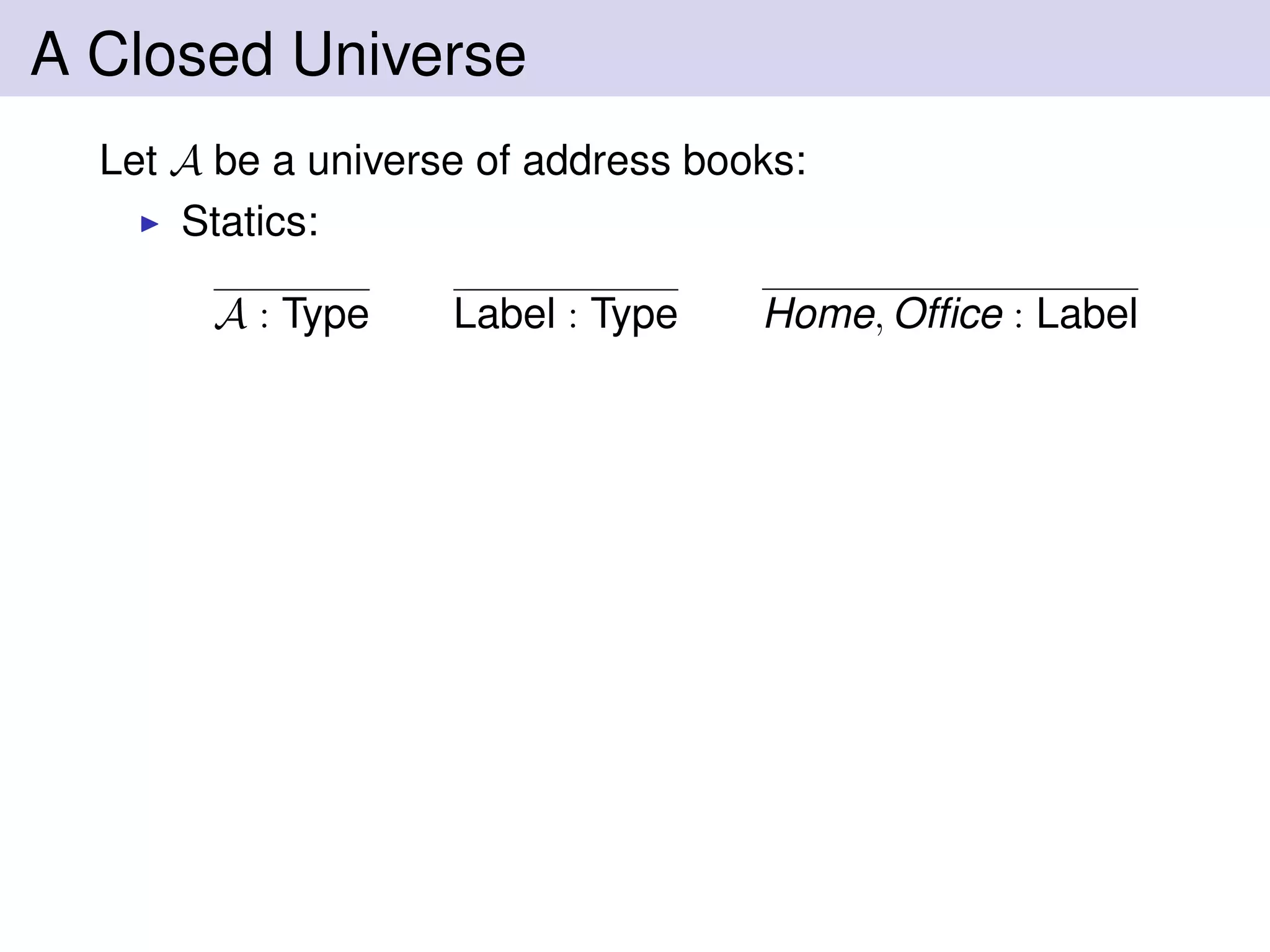
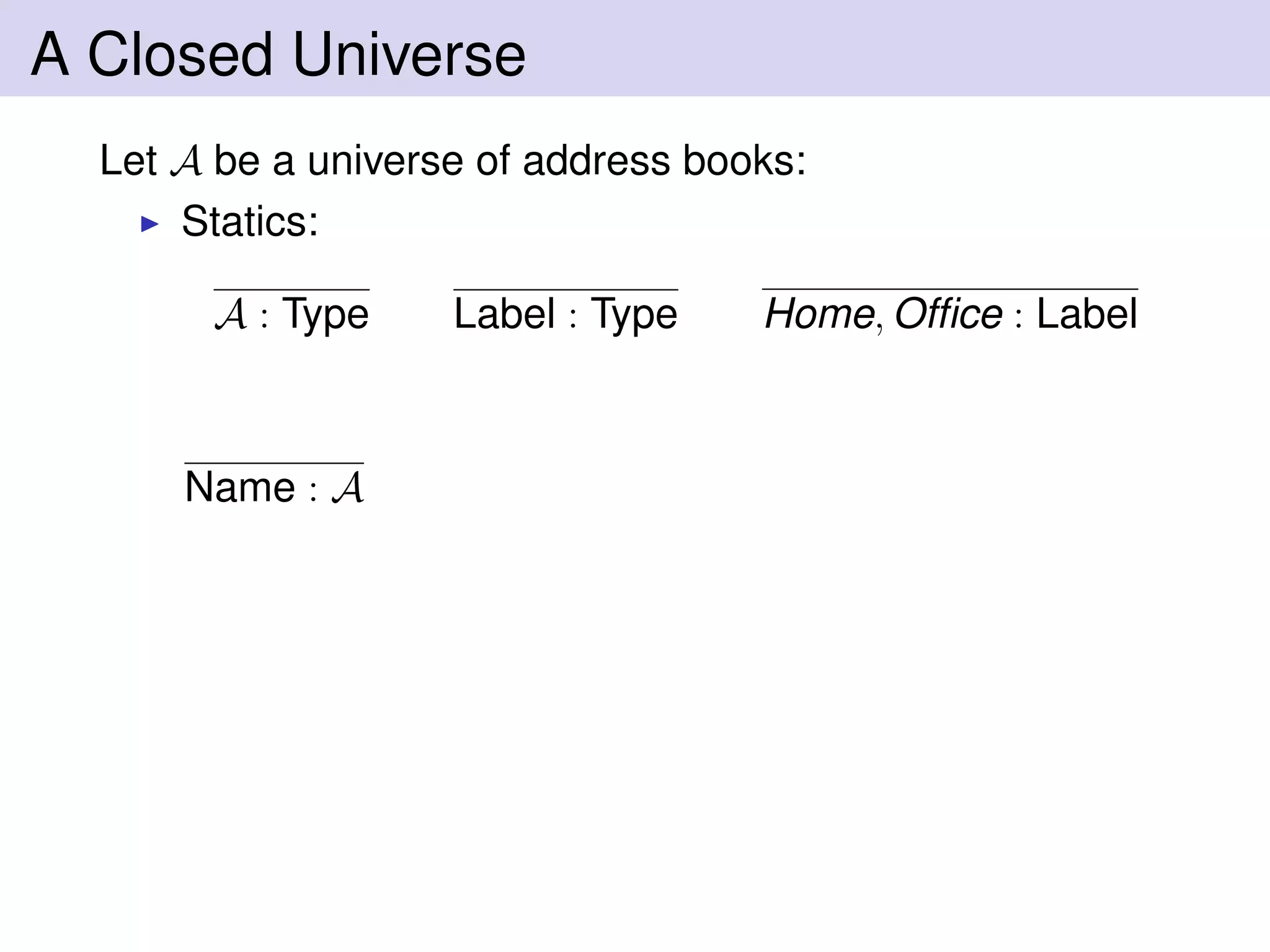
Let A be a universe of address books:
Statics:
A : Type Label : Type Home, Office : Label
Name : A
: Label
Phone[ ], Email[ ] : A](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-41-2048.jpg)
![A Closed Universe
Let A be a universe of address books:
Statics:
A : Type Label : Type Home, Office : Label
Name : A
: Label
Phone[ ], Email[ ] : A
s : A
ElA(s) : Type](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-42-2048.jpg)
![A Closed Universe
Let A be a universe of address books:
Statics:
A : Type Label : Type Home, Office : Label
Name : A
: Label
Phone[ ], Email[ ] : A
s : A
ElA(s) : Type
Dynamics:](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-43-2048.jpg)
![A Closed Universe
Let A be a universe of address books:
Statics:
A : Type Label : Type Home, Office : Label
Name : A
: Label
Phone[ ], Email[ ] : A
s : A
ElA(s) : Type
Dynamics:
ElA(Name) string](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-44-2048.jpg)
![A Closed Universe
Let A be a universe of address books:
Statics:
A : Type Label : Type Home, Office : Label
Name : A
: Label
Phone[ ], Email[ ] : A
s : A
ElA(s) : Type
Dynamics:
ElA(Name) string ElA(Email[ ]) string](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-45-2048.jpg)
![A Closed Universe
Let A be a universe of address books:
Statics:
A : Type Label : Type Home, Office : Label
Name : A
: Label
Phone[ ], Email[ ] : A
s : A
ElA(s) : Type
Dynamics:
ElA(Name) string ElA(Email[ ]) string
ElA(Phone[ ]) list(N)](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-46-2048.jpg)



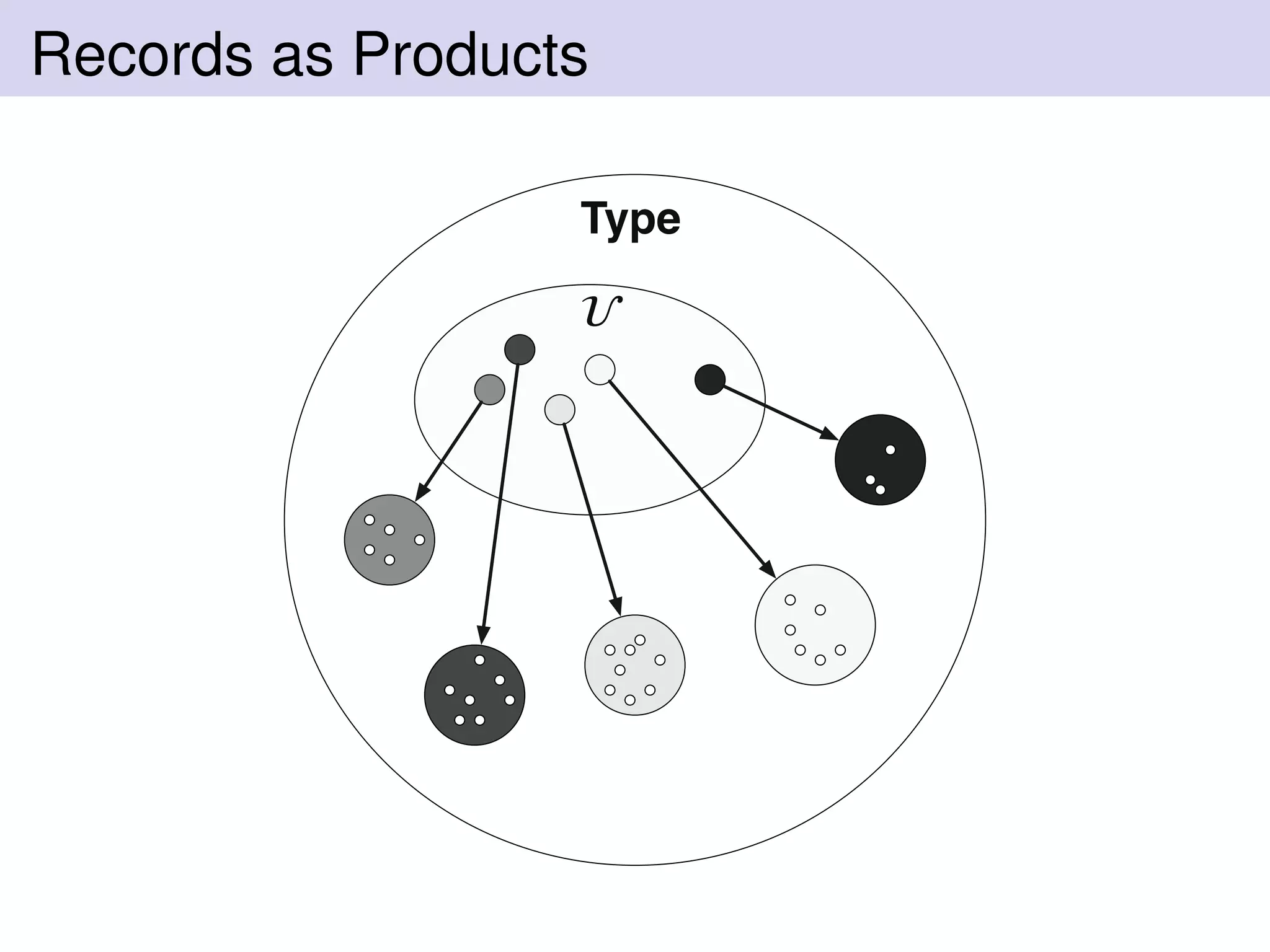



























![Records in Haskell
data Rec :: (U → ∗) → [ U ] → ∗ where](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-81-2048.jpg)
![Records in Haskell
data Rec :: (U → ∗) → [ U ] → ∗ where
RNil :: Rec elU ’[]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-82-2048.jpg)
![Records in Haskell
data Rec :: (U → ∗) → [ U ] → ∗ where
RNil :: Rec elU ’[]
(:&) :: !(elU r) → !(Rec elU rs) → Rec elU (r ’: rs)](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-83-2048.jpg)



![Records in Haskell (Actually)
data TyFun :: ∗ → ∗ → ∗
type family (f :: TyFun k l → ∗) $ (x :: k) :: l
data Rec :: (TyFun U ∗ → ∗) → [ U ] → ∗ where
RNil :: Rec elU ’[]
(:&) :: !(elU $ r) → !(Rec elU rs) → Rec elU (r ’: rs)](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-87-2048.jpg)



![Recovering HList
data Id :: (TyFun k k) → ∗ where
type instance Id $ x = x
type HList rs = Rec Id rs
ex :: HList [Z, Bool, String]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-91-2048.jpg)
![Recovering HList
data Id :: (TyFun k k) → ∗ where
type instance Id $ x = x
type HList rs = Rec Id rs
ex :: HList [Z, Bool, String]
ex = 34 :& True :& ”vinyl” :& RNil](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-92-2048.jpg)
![Validating Records
bob :: Rec ElA [Name, Email Work]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-93-2048.jpg)
![Validating Records
bob :: Rec ElA [Name, Email Work]
bob = Name =: ”Robert Harper”
⊕ Email Work =: ”rwh@cs.cmu.edu”](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-94-2048.jpg)
![Validating Records
bob :: Rec ElA [Name, Email Work]
bob = Name =: ”Robert Harper”
⊕ Email Work =: ”rwh@cs.cmu.edu”
validateName :: String → Either Error String
validateEmail :: String → Either Error String
validatePhone :: [N] → Either Error [N]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-95-2048.jpg)
![Validating Records
bob :: Rec ElA [Name, Email Work]
bob = Name =: ”Robert Harper”
⊕ Email Work =: ”rwh@cs.cmu.edu”
validateName :: String → Either Error String
validateEmail :: String → Either Error String
validatePhone :: [N] → Either Error [N]
*unnnnnhhh...*](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-96-2048.jpg)
![Validating Records
bob :: Rec ElA [Name, Email Work]
bob = Name =: ”Robert Harper”
⊕ Email Work =: ”rwh@cs.cmu.edu”
validateName :: String → Either Error String
validateEmail :: String → Either Error String
validatePhone :: [N] → Either Error [N]
*unnnnnhhh...*
validateContact
:: Rec ElA [Name, Email Work]
→ Either Error (Rec ElA [Name, Email Work])](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-97-2048.jpg)

![Effects inside records
data Rec :: (TyFun U ∗ → ∗) → [ U ] → ∗ where
RNil :: Rec elU ’[]
(:&) :: !(elU $ r) → !(Rec elU rs) → Rec elU (r ’: rs)](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-99-2048.jpg)
![Effects inside records
data Rec :: (TyFun U ∗ → ∗) → (∗ → ∗) → [ U ] → ∗ where
RNil :: Rec elU f ’[]
(:&) :: !(f (elU $ r)) → !(Rec elU f rs) → Rec elU f (r ’: rs)](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-100-2048.jpg)
![Effects inside records
data Rec :: (TyFun U ∗ → ∗) → (∗ → ∗) → [ U ] → ∗ where
RNil :: Rec elU f ’[]
(:&) :: !(f (elU $ r)) → !(Rec elU f rs) → Rec elU f (r ’: rs)
(=:) : Applicative f ⇒ sing r → elU $ r → Rec elU f ’[r]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-101-2048.jpg)
![Effects inside records
data Rec :: (TyFun U ∗ → ∗) → (∗ → ∗) → [ U ] → ∗ where
RNil :: Rec elU f ’[]
(:&) :: !(f (elU $ r)) → !(Rec elU f rs) → Rec elU f (r ’: rs)
(=:) : Applicative f ⇒ sing r → elU $ r → Rec elU f ’[r]
k =: x = pure x :& RNil](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-102-2048.jpg)
![Effects inside records
data Rec :: (TyFun U ∗ → ∗) → (∗ → ∗) → [ U ] → ∗ where
RNil :: Rec elU f ’[]
(:&) :: !(f (elU $ r)) → !(Rec elU f rs) → Rec elU f (r ’: rs)
(=:) : Applicative f ⇒ sing r → elU $ r → Rec elU f ’[r]
k =: x = pure x :& RNil
(⇐): sing r → f (elU $ r) → Rec elU f ’[r]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-103-2048.jpg)
![Effects inside records
data Rec :: (TyFun U ∗ → ∗) → (∗ → ∗) → [ U ] → ∗ where
RNil :: Rec elU f ’[]
(:&) :: !(f (elU $ r)) → !(Rec elU f rs) → Rec elU f (r ’: rs)
(=:) : Applicative f ⇒ sing r → elU $ r → Rec elU f ’[r]
k =: x = pure x :& RNil
(⇐): sing r → f (elU $ r) → Rec elU f ’[r]
k ⇐ x = x :& RNil](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-104-2048.jpg)

![Compositional Validation
type RecA = Rec ElA
bob :: RecA Identity [Name, Email Work]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-106-2048.jpg)
![Compositional Validation
type RecA = Rec ElA
bob :: RecA Identity [Name, Email Work]
bob = Name =: ”Robert Harper”
⊕ Email Work =: ”rwh@cs.cmu.edu”](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-107-2048.jpg)
![Compositional Validation
type RecA = Rec ElA
bob :: RecA Identity [Name, Email Work]
bob = Name =: ”Robert Harper”
⊕ Email Work =: ”rwh@cs.cmu.edu”](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-108-2048.jpg)

![Compositional Validation
type Validator a = a → Either Error a
validateName :: RecA Validator ’[Name]
validatePhone :: ∀ . RecA Validator ’[Phone ]
validateEmail :: ∀ . RecA Validator ’[Email ]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-110-2048.jpg)
![Compositional Validation
type Validator a = a → Either Error a
validateName :: RecA Validator ’[Name]
validatePhone :: ∀ . RecA Validator ’[Phone ]
validateEmail :: ∀ . RecA Validator ’[Email ]
type TotalContact =
[ Name, Email Home, Email Work
, Phone Home, Phone Work ]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-111-2048.jpg)
![Compositional Validation
type Validator a = a → Either Error a
validateName :: RecA Validator ’[Name]
validatePhone :: ∀ . RecA Validator ’[Phone ]
validateEmail :: ∀ . RecA Validator ’[Email ]
type TotalContact =
[ Name, Email Home, Email Work
, Phone Home, Phone Work ]
validateContact :: RecA Validator TotalContact
validateContact = validateName
⊕ validateEmail
⊕ validateEmail
⊕ validatePhone
⊕ validatePhone](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-112-2048.jpg)







![Compositional Validation
newtype Lift o f g x = Lift { runLift :: f x ‘o‘ g x }
type Validator = Lift (→) Identity (Either Error)
( ) :: RecU (Lift (→) f g) rs → RecU f rs → RecU g rs
rdist :: Applicative f ⇒ RecU f rs → f (RecU Identity rs)
validateContact :: RecA Validator TotalContact
bobValid :: RecA (Either Error) [Name, Email Work]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-120-2048.jpg)
![Compositional Validation
newtype Lift o f g x = Lift { runLift :: f x ‘o‘ g x }
type Validator = Lift (→) Identity (Either Error)
( ) :: RecU (Lift (→) f g) rs → RecU f rs → RecU g rs
rdist :: Applicative f ⇒ RecU f rs → f (RecU Identity rs)
validateContact :: RecA Validator TotalContact
bobValid :: RecA (Either Error) [Name, Email Work]
bobValid = cast validateContact bob](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-121-2048.jpg)
![Compositional Validation
newtype Lift o f g x = Lift { runLift :: f x ‘o‘ g x }
type Validator = Lift (→) Identity (Either Error)
( ) :: RecU (Lift (→) f g) rs → RecU f rs → RecU g rs
rdist :: Applicative f ⇒ RecU f rs → f (RecU Identity rs)
validateContact :: RecA Validator TotalContact
bobValid :: RecA (Either Error) [Name, Email Work]
bobValid = cast validateContact bob
validBob :: Either Error (RecA Identity [Name, Email Work])](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-122-2048.jpg)
![Compositional Validation
newtype Lift o f g x = Lift { runLift :: f x ‘o‘ g x }
type Validator = Lift (→) Identity (Either Error)
( ) :: RecU (Lift (→) f g) rs → RecU f rs → RecU g rs
rdist :: Applicative f ⇒ RecU f rs → f (RecU Identity rs)
validateContact :: RecA Validator TotalContact
bobValid :: RecA (Either Error) [Name, Email Work]
bobValid = cast validateContact bob
validBob :: Either Error (RecA Identity [Name, Email Work])
validBob = rdist bobValid](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-123-2048.jpg)






![Concurrent Records with Async
fetchName :: RecA IO ’[Name]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-130-2048.jpg)
![Concurrent Records with Async
fetchName :: RecA IO ’[Name]
fetchName = Name ⇐ someOperation](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-131-2048.jpg)
![Concurrent Records with Async
fetchName :: RecA IO ’[Name]
fetchName = Name ⇐ someOperation
fetchWorkEmail :: RecA IO ’[Email Work]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-132-2048.jpg)
![Concurrent Records with Async
fetchName :: RecA IO ’[Name]
fetchName = Name ⇐ someOperation
fetchWorkEmail :: RecA IO ’[Email Work]
fetchWorkEmail = Email Work ⇐ anotherOperation](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-133-2048.jpg)
![Concurrent Records with Async
fetchName :: RecA IO ’[Name]
fetchName = Name ⇐ someOperation
fetchWorkEmail :: RecA IO ’[Email Work]
fetchWorkEmail = Email Work ⇐ anotherOperation
fetchBob :: RecA IO [Name, Email Work]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-134-2048.jpg)
![Concurrent Records with Async
fetchName :: RecA IO ’[Name]
fetchName = Name ⇐ someOperation
fetchWorkEmail :: RecA IO ’[Email Work]
fetchWorkEmail = Email Work ⇐ anotherOperation
fetchBob :: RecA IO [Name, Email Work]
fetchBob = fetchName ⊕ fetchWorkEmail](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-135-2048.jpg)



![Concurrent Records with Async
newtype Concurrently a
= Concurrently { runConcurrently :: IO a }
( $ ) :: (∀ a. f a → g a) → RecU f rs → RecU g rs
bobConcurrently :: RecA Concurrently [Name, Email Work]](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-139-2048.jpg)
![Concurrent Records with Async
newtype Concurrently a
= Concurrently { runConcurrently :: IO a }
( $ ) :: (∀ a. f a → g a) → RecU f rs → RecU g rs
bobConcurrently :: RecA Concurrently [Name, Email Work]
bobConcurrently = Concurrently $ fetchBob](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-140-2048.jpg)
![Concurrent Records with Async
newtype Concurrently a
= Concurrently { runConcurrently :: IO a }
( $ ) :: (∀ a. f a → g a) → RecU f rs → RecU g rs
bobConcurrently :: RecA Concurrently [Name, Email Work]
bobConcurrently = Concurrently $ fetchBob
concurrentBob :: Concurrently (RecA Identity [...])](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-141-2048.jpg)
![Concurrent Records with Async
newtype Concurrently a
= Concurrently { runConcurrently :: IO a }
( $ ) :: (∀ a. f a → g a) → RecU f rs → RecU g rs
bobConcurrently :: RecA Concurrently [Name, Email Work]
bobConcurrently = Concurrently $ fetchBob
concurrentBob :: Concurrently (RecA Identity [...])
concurrentBob = rdist bobConcurrently](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-142-2048.jpg)

![Concurrent Records with Async
fetchBob :: RecA IO [Name, Email Work]
bobConcurrently :: RecA Concurrently [Name, Email Work]
concurrentBob :: Concurrently (RecA Identity [...])](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-144-2048.jpg)
![Concurrent Records with Async
fetchBob :: RecA IO [Name, Email Work]
bobConcurrently :: RecA Concurrently [Name, Email Work]
concurrentBob :: Concurrently (RecA Identity [...])
bob :: IO (RecA Identity [Name, Email Work])](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-145-2048.jpg)
![Concurrent Records with Async
fetchBob :: RecA IO [Name, Email Work]
bobConcurrently :: RecA Concurrently [Name, Email Work]
concurrentBob :: Concurrently (RecA Identity [...])
bob :: IO (RecA Identity [Name, Email Work])
bob = runConcurrently concurrentBob](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-146-2048.jpg)










![A Menagerie of Quantifiers
Dependent Products:
Γ A : Type Γ, x : A B : Type
Γ A B : Type
Γ, x : A e : B[x]
Γ λx.e : A B](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-158-2048.jpg)
![A Menagerie of Quantifiers
Dependent Sums:
Γ A : Type Γ, x : A B : Type
Γ A B : Type
Γ a : A Γ b : B[a]
Γ a, b : A B](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-159-2048.jpg)
![A Menagerie of Quantifiers
Inductive Types:
Γ A : Type Γ, x : A B : Type
Γ WA B : Type
Γ a : A Γ, v : B[a] b : WA B
Γ sup(a; v. b) : WA B](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-160-2048.jpg)
![A Menagerie of Quantifiers
Coinductive Types:
Γ A : Type Γ, x : A B : Type
Γ MA B : Type
Γ a : A Γ, v : B[a] b : ∞ (MA B)
Γ inf(a; v. b) : MA B](https://image.slidesharecdn.com/talk-140606100042-phpapp02/75/Programming-in-Vinyl-BayHac-2014-161-2048.jpg)