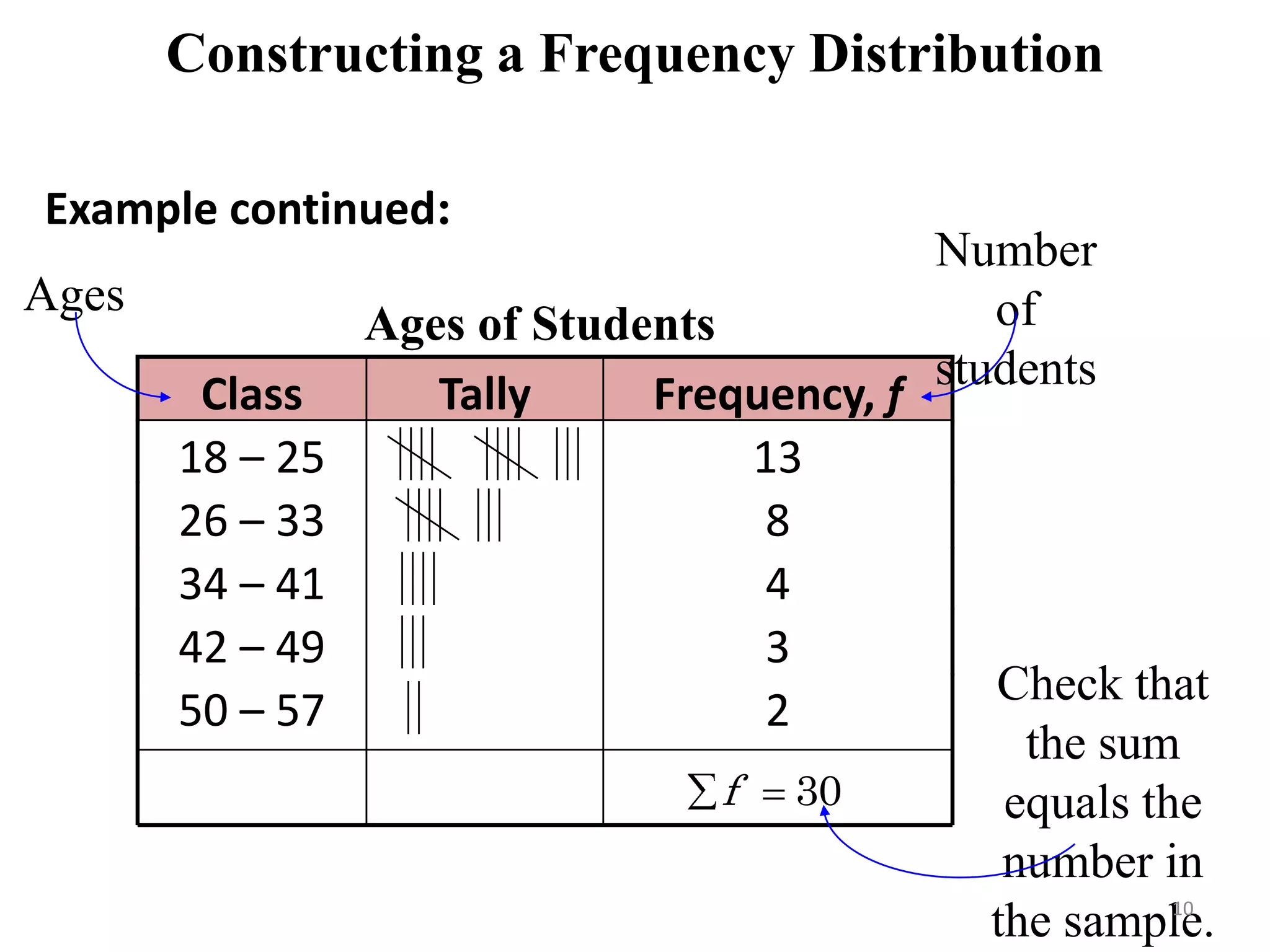
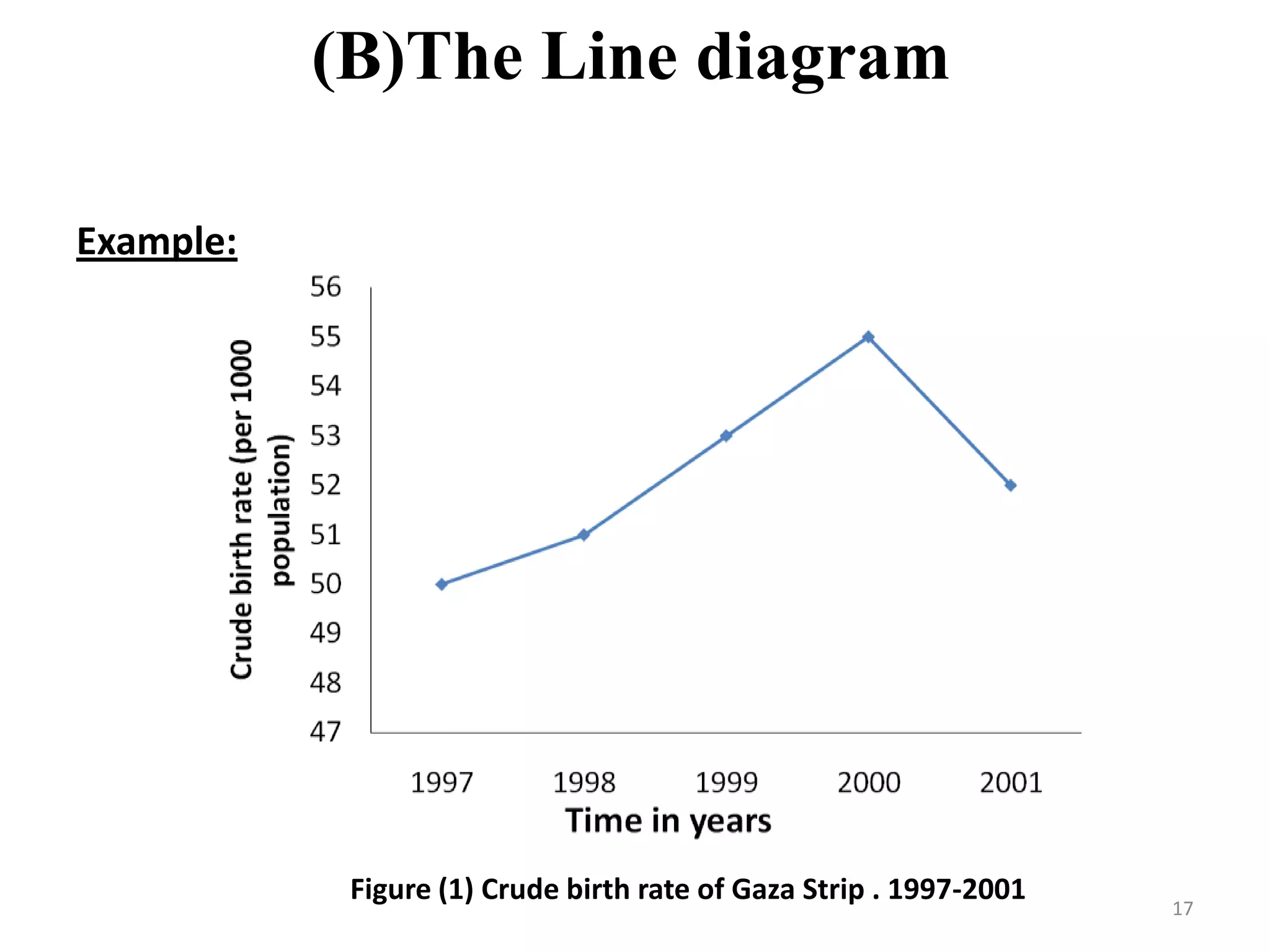
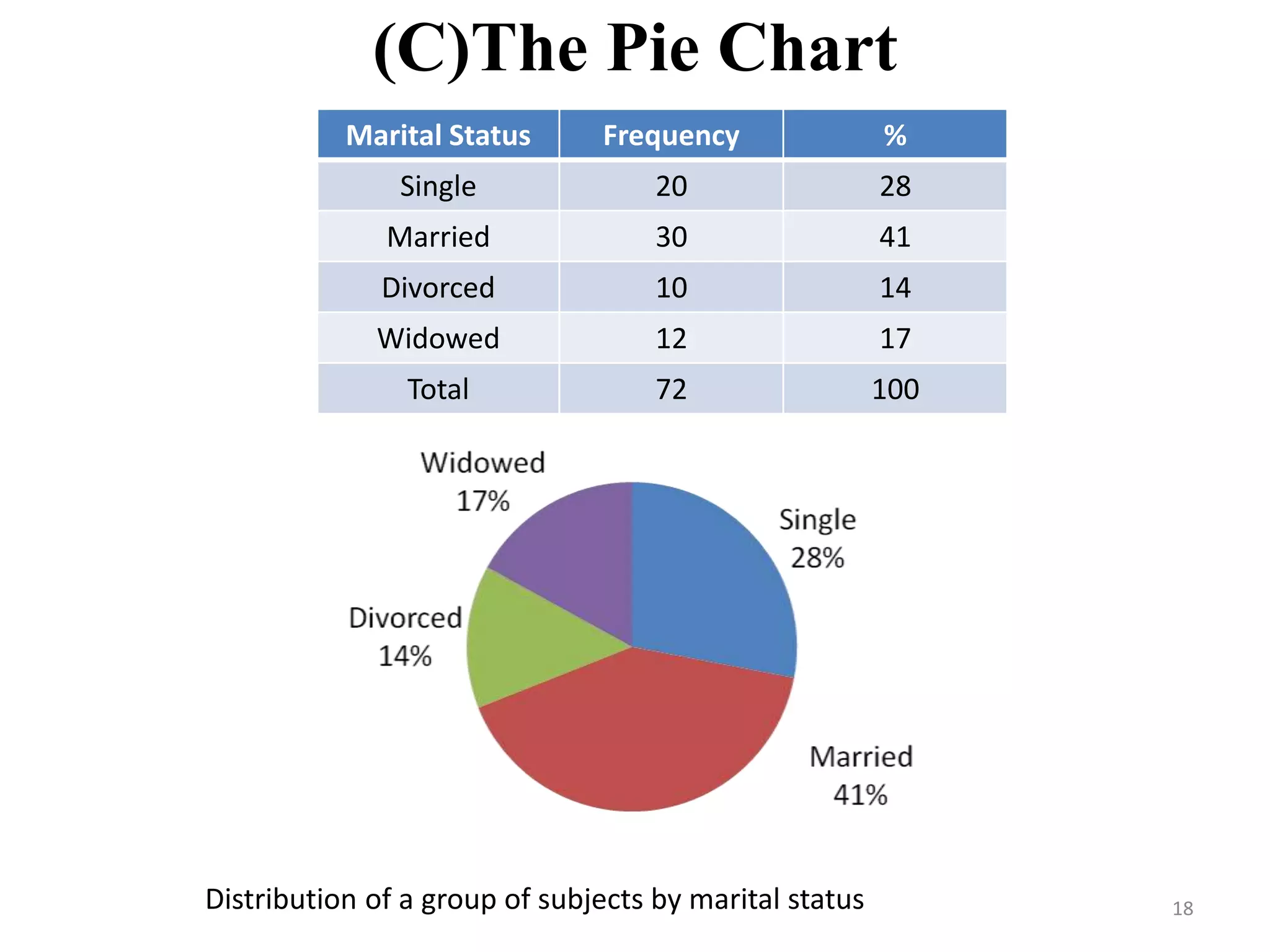
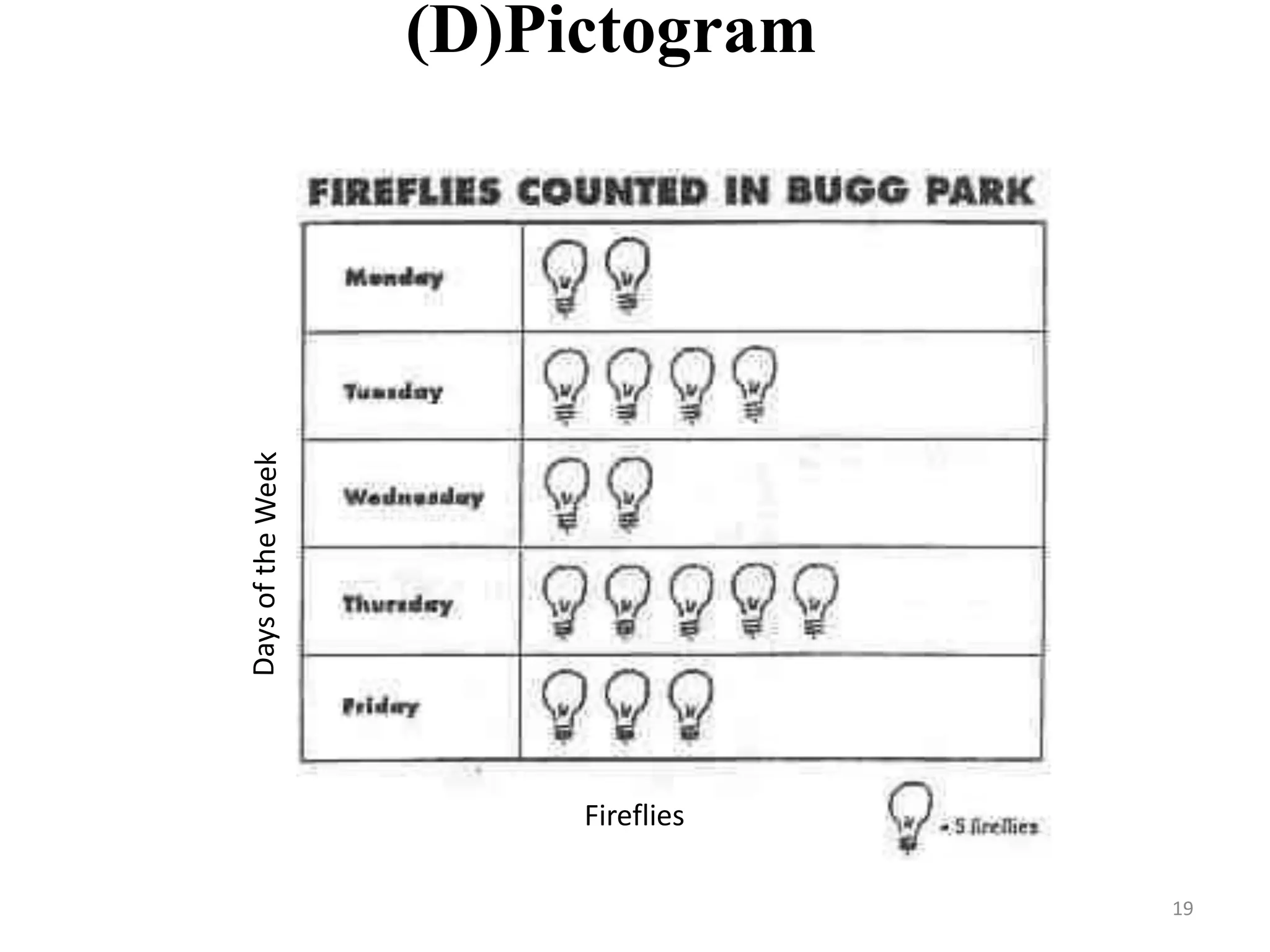
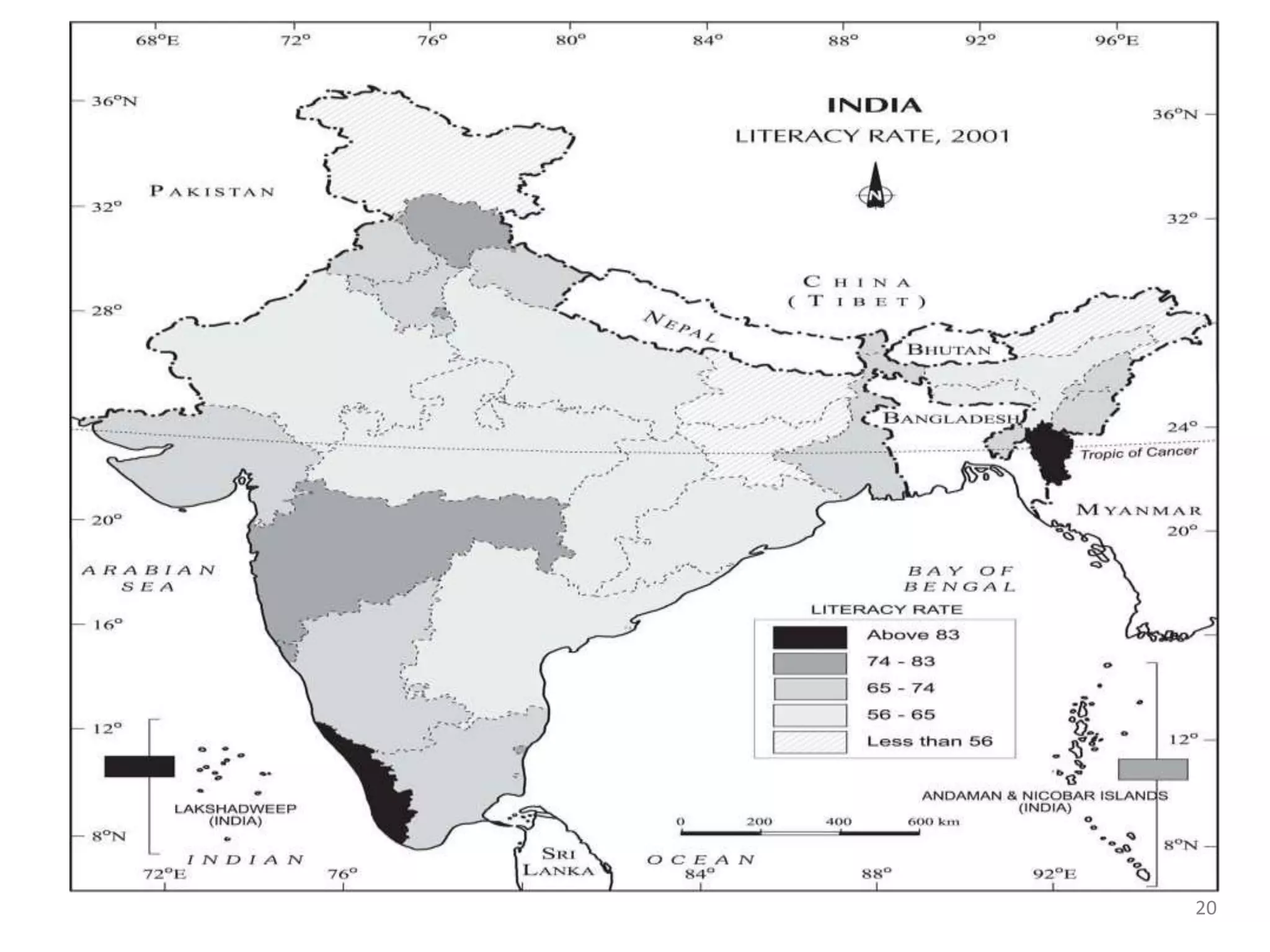
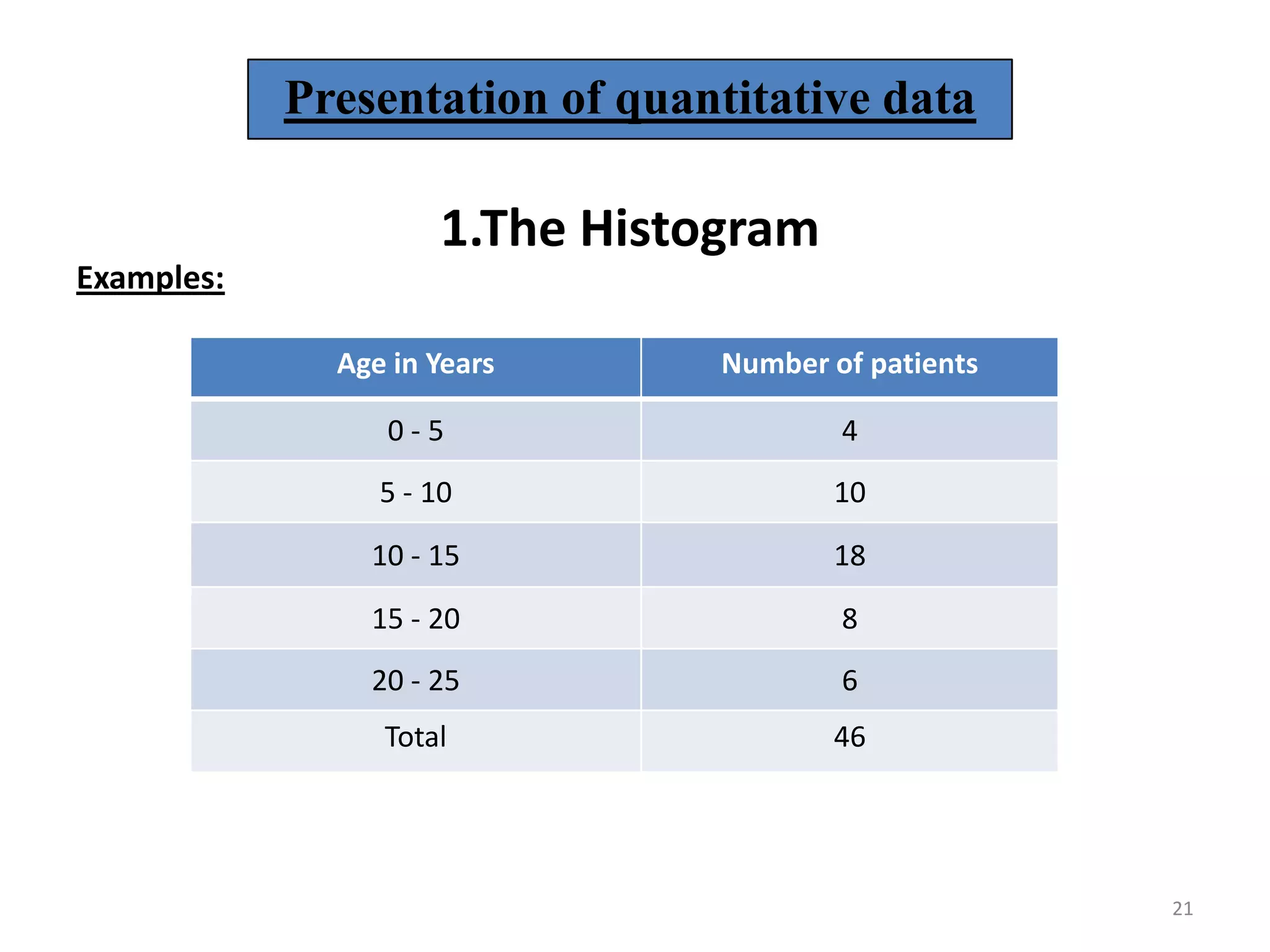
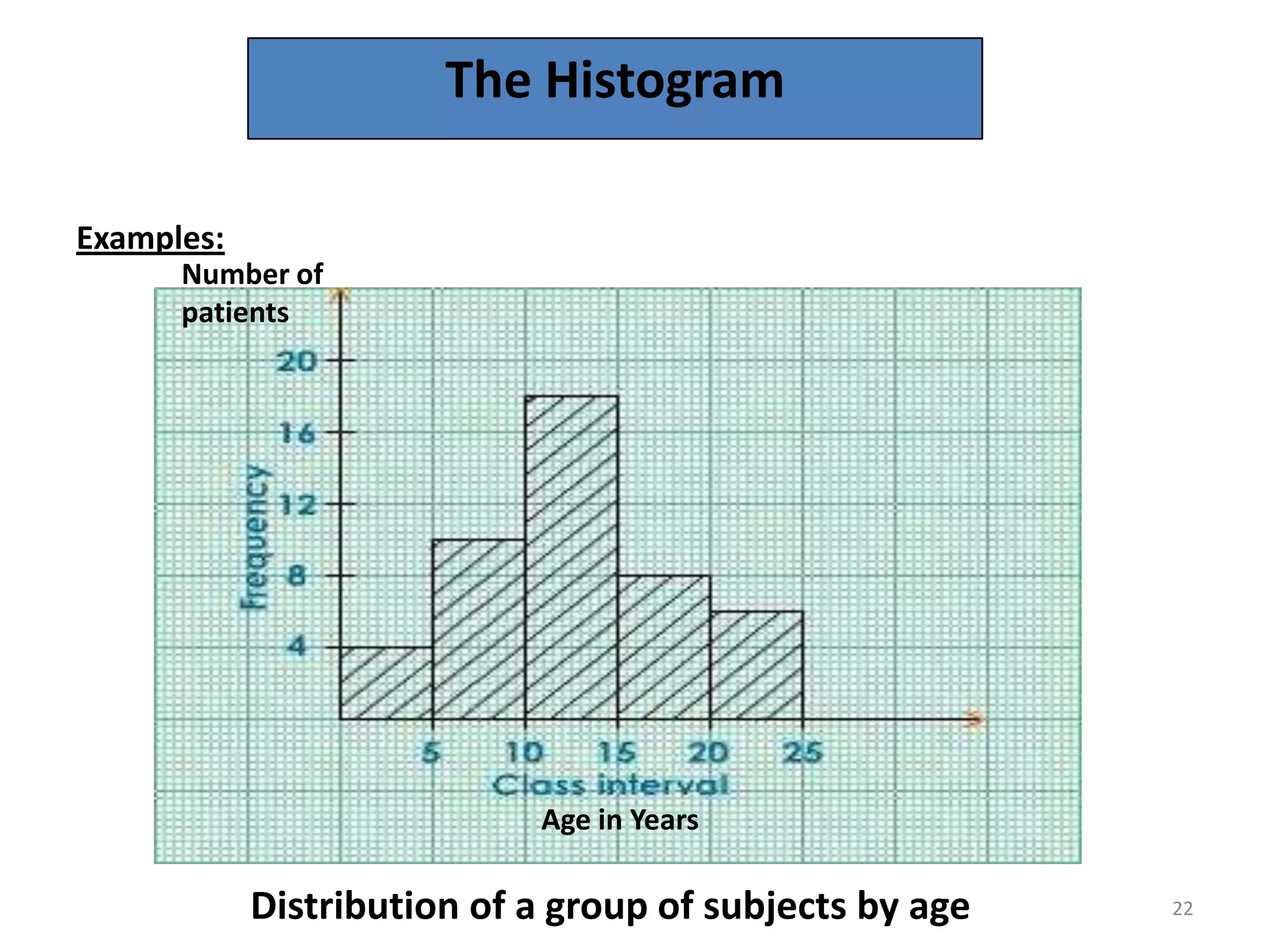
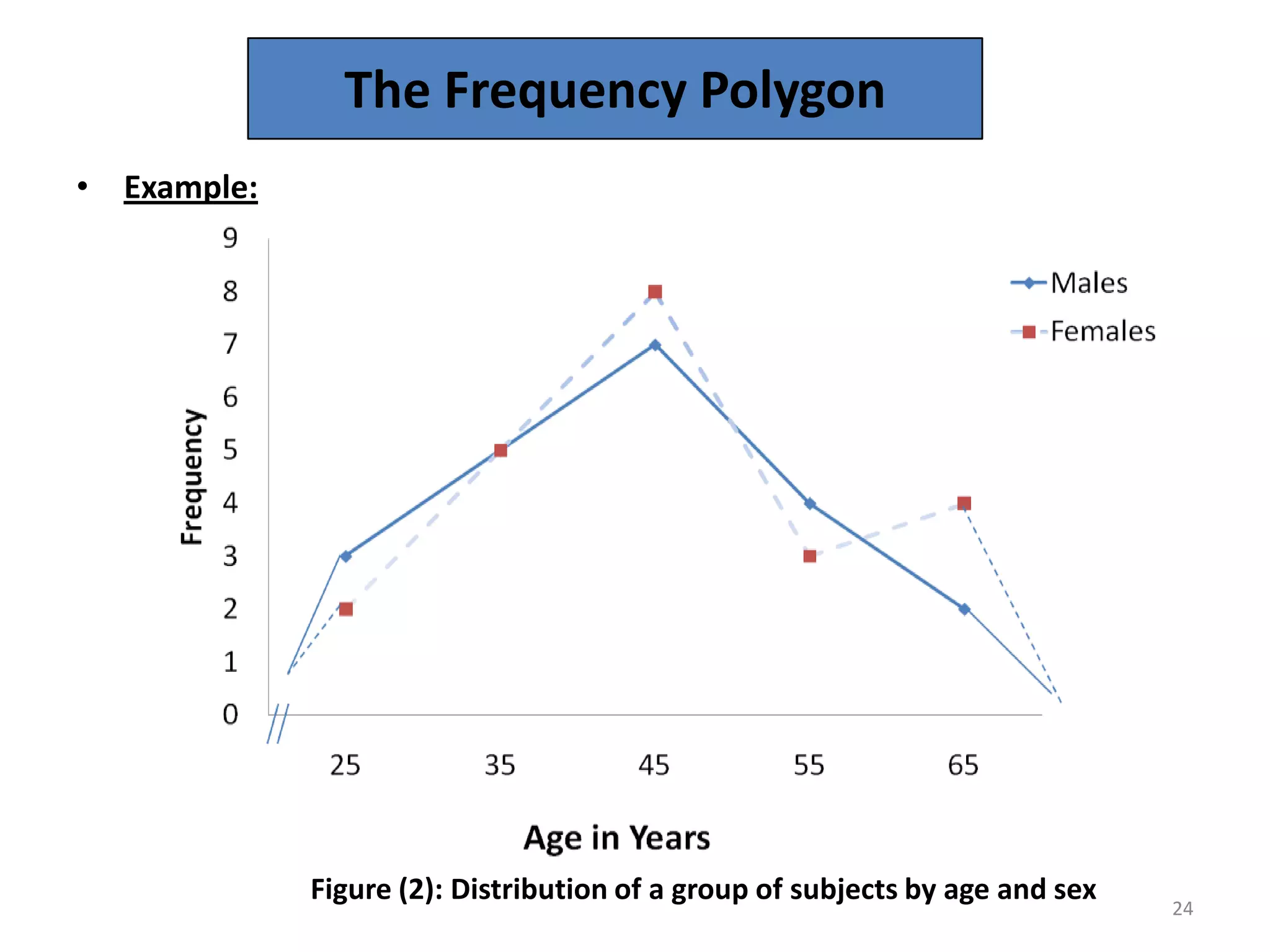
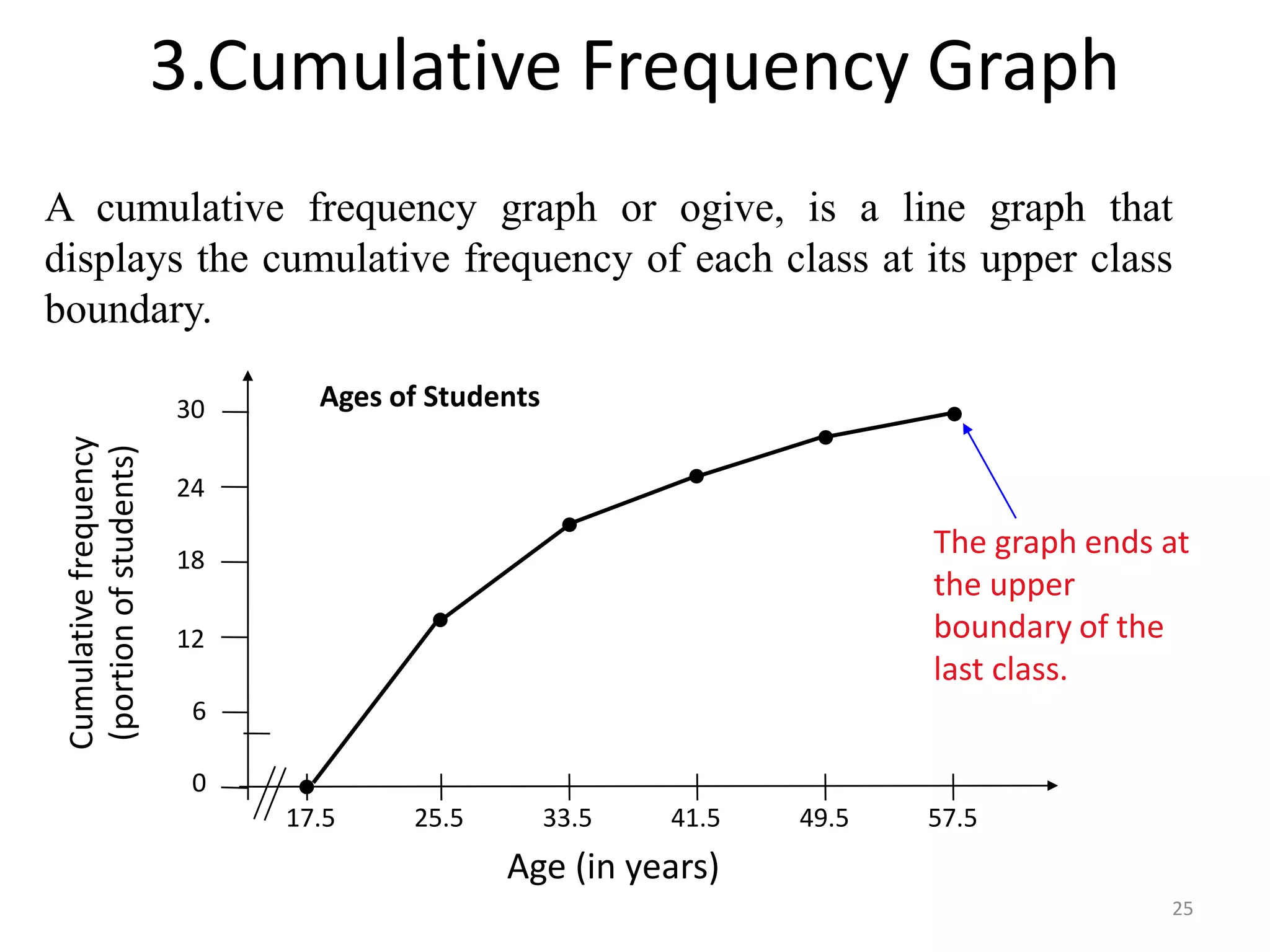
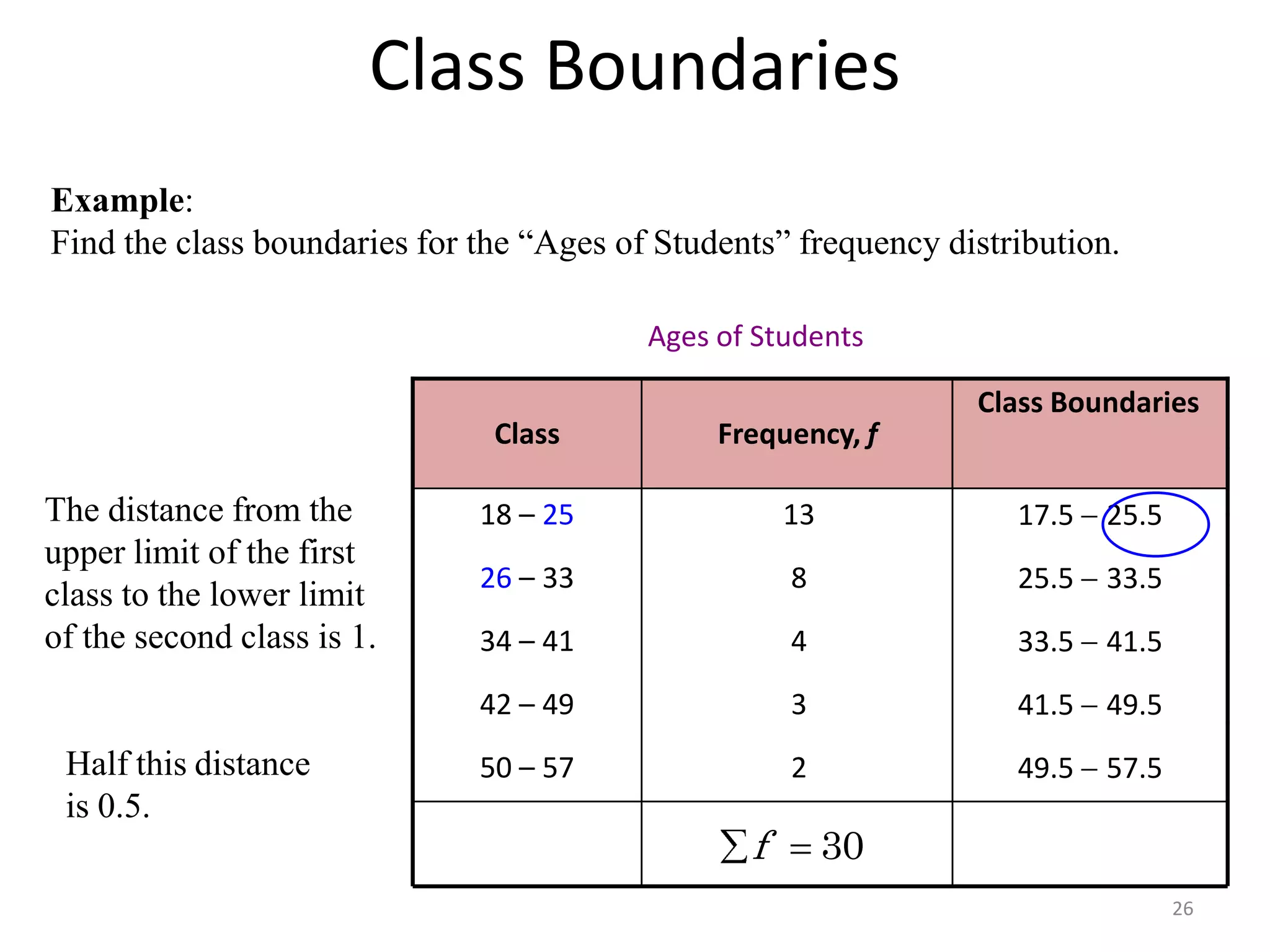
This document discusses various methods of data presentation. It describes quantitative and qualitative data and how to construct frequency distributions through grouping data into classes and calculating frequencies. It also discusses how to calculate relative frequencies, cumulative frequencies, class boundaries, midpoints and how to present data graphically through histograms, frequency polygons, cumulative frequency curves, bar charts, pie charts and scatter diagrams. The document provides examples and guidelines for constructing each of these data presentation methods.