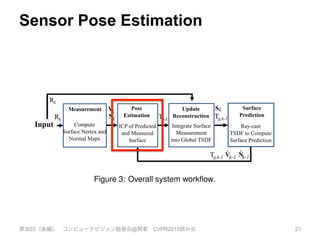
DynamicFusion is a method for reconstructing and tracking non-rigid scenes in real-time by extending KinectFusion. It uses a volumetric truncated signed distance function (TSDF) to integrate depth maps from multiple viewpoints into a global reconstruction. Live depth frames are aligned to a dense surface prediction generated by raycasting the TSDF. This closes the loop between mapping and localization for tracking dynamic, non-rigid scenes.







![Overview:
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 8
Rk Tg,k
Rk
Tg,k-1
Input
Measurement Pose
Estimation
Update
Reconstruction
Surface
Prediction
Compute
Surface Nertex and
Normal Maps
ICP of Predicted
and Measured
Surface
Integrate Surface
Measurement
into Global TSDF
Ray-cast
TSDF to Compute
Surface Prediction
Tg,k-1
k
Vk-1
S
Nk-1
^ ^
Vk
Nk
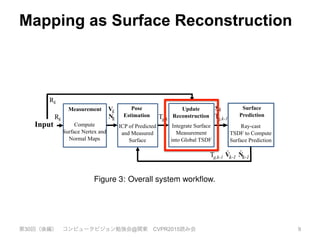
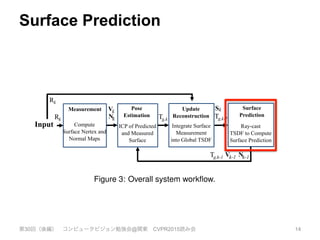
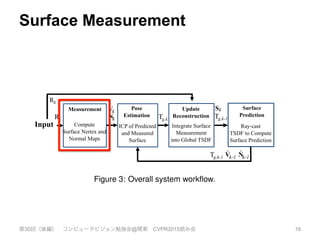
Figure 3: Overall system workflow.
Surface reconstruction update: The global scene fusion pro-
cess, where given the pose determined by tracking the depth data
from a new sensor frame, the surface measurement is integrated into
the scene model maintained with a volumetric, truncated signed dis-
tance function (TSDF) representation.
Surface prediction: Unlike frame-to-frame pose estimation as
performed in [15], we close the loop between mapping and local-
isation by tracking the live depth frame against the globally fused
model. This is performed by raycasting the signed distance func-
tion into the estimated frame to provide a dense surface prediction
against which the live depth map is aligned.
Figure 4: A s
showing the tru
field around the
had a valid mea
bouring map ve
Nk(u) = n
⇥
(V
on dy-
moving
move.
ects.
UIST’11, October 16–19, 2011, Santa Barbara, CA, USA](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-8-320.jpg)

![Mapping as Surface Reconstruction (3/4)
• Live Frame (Depth map) からTSDFへの変換
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 12
resents the distance to the nearest surface point.
Although efficient algorithms exist for computing the true dis-
crete SDF for a given set of point measurements (complexity is
linear in the the number of voxels) [22], sophisticated implemen-
tations are required to achieve top performance on GPU hardware,
without which real-time computation is not possible for a reason-
able size volume. Instead, we use a projective truncated signed
distance function that is readily computed and trivially parallelis-
able. For a raw depth map Rk with a known pose Tg,k, its global
frame projective TSDF [FRk
,WRk
] at a point p in the global frame
g is computed as,
FRk
(p) = Y
⇣
l 1
k(tg,k pk2 Rk(x)
⌘
, (6)
l = kK 1
˙xk2 , (7)
x =
j
p
⇣
KT 1
g,kp
⌘k
, (8)
Y(h) =
(
min
⇣
1, h
µ
⌘
sgn(h) iff h µ
null otherwise
(9)
We use a nearest neighbour lookup b.c instead of interpolating
the depth value, to prevent smearing of measurements at depth dis-
continuities. 1/l converts the ray distance to p to a depth (we found
no considerable difference in using SDF values computed using dis-
tances along the ray or along the optical axis). Y performs the SDF
truncation. The truncation function is scaled to ensure that a sur-
face measurement (zero crossing in the SDF) is represented by at
least one non truncated voxel value in the discretised volume ei-
ther side of the surface. Also, the support is increased linearly with
distance from the sensor center to support correct representation
of noisier measurements. The associated weight WRk
(p) is propor-
tional to cos(q)/Rk(x), where q is the angle between the associated
pixel ray direction and the surface normal measurement in the local
k
Wk 1(p)+WRk
(p
Wk(p) = Wk 1(p)+WRk
(p)
No update on the global TSDF is performed fo
from unmeasurable regions specified in Equation
provides weighting of the TSDF proportional to
surface measurement, we have also found that i
letting WRk
(p) = 1, resulting in a simple average,
sults. Moreover, by truncating the updated weigh
Wh ,
Wk(p) min(Wk 1(p)+WRk
(p),W
a moving average surface reconstruction can be o
reconstruction in scenes with dynamic object mot
Although a large number of voxels can be vis
project into the current image, the simplicity of
operation time is memory, not computation, bound
GPU hardware over 65 gigavoxels/second (⇡ 2m
update for a 5123 voxel reconstruction) can be up
bits per component in S(p), although experiment
ified that as few as 6 bits are required for the SD
we note that the raw depth measurements are used
rather than the bilateral filtered version used in t
ponent, described later in section 3.5. The early
desired high frequency structure and noise alike
duce the ability to reconstruct finer scale structure
3.4 Surface Prediction from Ray Casting
With the most up-to-date reconstruction availabl
ity to compute a dense surface prediction by rend
encoded in the zero level set Fk = 0 into a virtua
current estimate Tg,k. The surface prediction is s
and normal map ˆVk and ˆNk in frame of referenc
able size volume. Instead, we use a projective truncated signed
distance function that is readily computed and trivially parallelis-
able. For a raw depth map Rk with a known pose Tg,k, its global
rame projective TSDF [FRk
,WRk
] at a point p in the global frame
g is computed as,
FRk
(p) = Y
⇣
l 1
k(tg,k pk2 Rk(x)
⌘
, (6)
l = kK 1
˙xk2 , (7)
x =
j
p
⇣
KT 1
g,kp
⌘k
, (8)
Y(h) =
(
min
⇣
1, h
µ
⌘
sgn(h) iff h µ
null otherwise
(9)
We use a nearest neighbour lookup b.c instead of interpolating
he depth value, to prevent smearing of measurements at depth dis-
continuities. 1/l converts the ray distance to p to a depth (we found
no considerable difference in using SDF values computed using dis-
ances along the ray or along the optical axis). Y performs the SDF
runcation. The truncation function is scaled to ensure that a sur-
ace measurement (zero crossing in the SDF) is represented by at
east one non truncated voxel value in the discretised volume ei-
provides weig
surface measu
letting WRk
(p
sults. Moreov
Wh ,
W
a moving ave
reconstruction
Although a
project into th
operation time
GPU hardwar
update for a 5
bits per comp
ified that as fe
we note that th
rather than th
ponent, descr
desired high f
duce the abilit
3.4 Surfac
: 点pにおけるTSDF value : 点pにおける重み
continuities. 1/l converts the ray distance to p to a depth (we found
no considerable difference in using SDF values computed using dis-
tances along the ray or along the optical axis). Y performs the SDF
truncation. The truncation function is scaled to ensure that a sur-
face measurement (zero crossing in the SDF) is represented by at
least one non truncated voxel value in the discretised volume ei-
ther side of the surface. Also, the support is increased linearly with
distance from the sensor center to support correct representation
of noisier measurements. The associated weight WRk
(p) is propor-
tional to cos(q)/Rk(x), where q is the angle between the associated
pixel ray direction and the surface normal measurement in the local
frame.
The projective TSDF measurement is only correct exactly at the
surface FRk
(p) = 0 or if there is only a single point measurement
in isolation. When a surface is present the closest point along a
ray could be another surface point not on the ray associated with
the pixel in Equation 8. It has been shown that for points close
to the surface, a correction can be applied by scaling the SDF by
cos(q) [11]. However, we have found that approximation within
the truncation region for 100s or more fused TSDFs from multiple
viewpoints (as performed here) converges towards an SDF with a
pseudo-Euclidean metric that does not hinder mapping and tracking
performance.
ponent, described late
desired high frequenc
duce the ability to rec
3.4 Surface Pred
With the most up-to-
ity to compute a dens
encoded in the zero le
current estimate Tg,k.
and normal map ˆVk a
the subsequent camer
As we have a dense
SDF, a per pixel rayc
responding ray, Tg,kK
depth for the pixel a
ve for a visible surf
Marching also stops
mately when exiting t
face measurement at t
For points on or ve
is assumed that the gr
zero level set, and so
no considerable difference in using
tances along the ray or along the op
truncation. The truncation functio
face measurement (zero crossing i
least one non truncated voxel valu
ther side of the surface. Also, the s
distance from the sensor center to
of noisier measurements. The assoc
tional to cos(q)/Rk(x), where q is
pixel ray direction and the surface n
frame.
The projective TSDF measurem
surface FRk
(p) = 0 or if there is o
in isolation. When a surface is pr
ray could be another surface point
the pixel in Equation 8. It has be
to the surface, a correction can be
cos(q) [11]. However, we have fo
the truncation region for 100s or m
viewpoints (as performed here) co
pseudo-Euclidean metric that does
performance.
We use a nearest neighbour lookup b.c instead of interpolating
the depth value, to prevent smearing of measurements at depth dis-
continuities. 1/l converts the ray distance to p to a depth (we found
no considerable difference in using SDF values computed using dis-
tances along the ray or along the optical axis). Y performs the SDF
truncation. The truncation function is scaled to ensure that a sur-
face measurement (zero crossing in the SDF) is represented by at
least one non truncated voxel value in the discretised volume ei-
ther side of the surface. Also, the support is increased linearly with
distance from the sensor center to support correct representation
of noisier measurements. The associated weight WRk
(p) is propor-
tional to cos(q)/Rk(x), where q is the angle between the associated
pixel ray direction and the surface normal measurement in the local
frame.
The projective TSDF measurement is only correct exactly at the
surface FRk
(p) = 0 or if there is only a single point measurement
in isolation. When a surface is present the closest point along a
ray could be another surface point not on the ray associated with
the pixel in Equation 8. It has been shown that for points close
to the surface, a correction can be applied by scaling the SDF by
cos(q) [11]. However, we have found that approximation within
the truncation region for 100s or more fused TSDFs from multiple
viewpoints (as performed here) converges towards an SDF with a
pseudo-Euclidean metric that does not hinder mapping and tracking
performance.
we note that the
rather than the b
ponent, describe
desired high fre
duce the ability
3.4 Surface P
With the most u
ity to compute a
encoded in the z
current estimate
and normal map
the subsequent c
As we have a
SDF, a per pixe
responding ray,
depth for the p
ve for a visible
Marching also s
mately when exi
face measureme
For points on
is assumed that
zero level set, an
=
θ : Rayと法線のなす角
p
x
Global TSDF
Raw Depth map
µ
Rk(x)](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-12-320.jpg)
![Mapping as Surface Reconstruction (4/4)
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 13
実際のところ、 でいい結果になるらしい。
(5)
h map Rk) pro-
reconstructed.
a depth mea-
f the measured
ong each depth
ee space (here
ixel ray). Sec-
ained in the re-
he camera ray.
of uncertainty
µ. A TSDF
n measurement
e within visible
urface interface
e points farther
e the SDF rep-
g the true dis-
(complexity is
ted implemen-
GPU hardware,
e for a reason-
uncated signed
ally parallelis-
Tg,k, its global
e global frame
depth map, which can be seen as de-noising the global TSDF from
multiple noisy TSDF measurements. Under an L2 norm the de-
noised (fused) surface results as the zero-crossings of the point-wise
SDF F minimising:
min
F2F
Â
k
kWRk
FRk
F)k2. (10)
Given that the focus of our work is on real-time sensor tracking and
surface reconstruction we must maintain interactive frame-rates.
(For a 640x480 depth stream at 30fps the equivalent of over 9
million new point measurements are made per second). Storing
a weight Wk(p) with each value allows an important aspect of the
global minimum of the convex L2 de-noising metric to be exploited
for real-time fusion; that the solution can be obtained incrementally
as more data terms are added using a simple weighted running av-
erage [7], defined point-wise {p|FRk
(p) 6= null}:
Fk(p) =
Wk 1(p)Fk 1(p)+WRk
(p)FRk
(p)
Wk 1(p)+WRk
(p)
(11)
Wk(p) = Wk 1(p)+WRk
(p) (12)
No update on the global TSDF is performed for values resulting
from unmeasurable regions specified in Equation 9. While Wk(p)
provides weighting of the TSDF proportional to the uncertainty of
surface measurement, we have also found that in practice simply
letting WRk
(p) = 1, resulting in a simple average, provides good re-
sults. Moreover, by truncating the updated weight over some value
Wh ,
Wk(p) min(Wk 1(p)+WRk
(p),Wh ) , (13)
a weight Wk(p) with each value allows an important aspect of the
global minimum of the convex L2 de-noising metric to be exploited
for real-time fusion; that the solution can be obtained incrementally
as more data terms are added using a simple weighted running av-
erage [7], defined point-wise {p|FRk
(p) 6= null}:
Fk(p) =
Wk 1(p)Fk 1(p)+WRk
(p)FRk
(p)
Wk 1(p)+WRk
(p)
(11)
Wk(p) = Wk 1(p)+WRk
(p) (12)
No update on the global TSDF is performed for values resulting
from unmeasurable regions specified in Equation 9. While Wk(p)
provides weighting of the TSDF proportional to the uncertainty of
surface measurement, we have also found that in practice simply
letting WRk
(p) = 1, resulting in a simple average, provides good re-
sults. Moreover, by truncating the updated weight over some value
Wh ,
Given that the focus of our work is on real-time sensor trackin
surface reconstruction we must maintain interactive frame-
(For a 640x480 depth stream at 30fps the equivalent of o
million new point measurements are made per second). S
a weight Wk(p) with each value allows an important aspect
global minimum of the convex L2 de-noising metric to be exp
for real-time fusion; that the solution can be obtained increme
as more data terms are added using a simple weighted runnin
erage [7], defined point-wise {p|FRk
(p) 6= null}:
Fk(p) =
Wk 1(p)Fk 1(p)+WRk
(p)FRk
(p)
Wk 1(p)+WRk
(p)
Wk(p) = Wk 1(p)+WRk
(p)
No update on the global TSDF is performed for values res
from unmeasurable regions specified in Equation 9. While W
provides weighting of the TSDF proportional to the uncertai
Global SceneとLive FrameのTSDFのFusion
重みの更新
FusionされたTSDF Value
Global Model Live Frame](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-13-320.jpg)


![Surface Measurement (2/4)
• De-noise
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 18
provides calibrated depth measurements Rk(u) 2 R at each image
pixel u = (u,v)> in the image domain u 2 U ⇢ R2 such that pk =
Rk(u)K 1 ˙u is a metric point measurement in the sensor frame of
reference k. We apply a bilateral filter [27] to the raw depth map to
obtain a discontinuity preserved depth map with reduced noise Dk,
Dk(u) =
1
Wp
Â
q2U
Nss (ku qk2)Nsr (kRk(u) Rk(q)k2)Rk(q) ,
(2)
where Ns (t) = exp( t2s 2) and Wp is a normalizing constant.
We back-project the filtered depth values into the sensor’s frame
of reference to obtain a vertex map Vk,
Vk(u) = Dk(u)K 1
˙u . (3)
Since each frame from the depth sensor is a surface measurement
on a regular grid, we compute, using a cross product between neigh-
[7]
the
fac
vis
on
ple
a g
low
wit
fus
Sk(
rec
olu
res
vox
and
ra calibration matrix
e into image pixels.
e projection of p 2
to obtain q 2 R2 =
denote homogeneous
depth map Rk which
u) 2 R at each image
⇢ R2 such that pk =
the sensor frame of
the raw depth map to
th reduced noise Dk,
) Rk(q)k2)Rk(q) ,
(2)
corresponding depth map level. We note that
global co-ordinate frame transform Tg,k associ
measurement, the global frame vertex is V
g
k(
the equivalent mapping of normal vectors int
N
g
k(u) = Rg,kNk(u).
3.3 Mapping as Surface Reconstructio
Each consecutive depth frame, with an associa
estimate, is fused incrementally into one sing
using the volumetric truncated signed distan
[7]. In a true signed distance function, the v
the signed distance to the closest zero crossin
face), taking on positive and increasing valu
visible surface into free space, and negative a
on the non-visible side. The result of averagin
ple 3D point clouds (or surface measurements)
a global frame is a global surface fusion.
An example given in Figure 4 demonstrate
lows us to represent arbitrary genus surface
: Raw Depth map
We will also use a single constant camera calibration matri
K that transforms points on the sensor plane into image pixel
The function q = p(p) performs perspective projection of p
R3 = (x,y,z)> including dehomogenisation to obtain q 2 R2 =
(x/z,y/z)>. We will also use a dot notation to denote homogeneou
vectors ˙u := (u>|1)>
3.2 Surface Measurement
At time k a measurement comprises a raw depth map Rk whic
provides calibrated depth measurements Rk(u) 2 R at each imag
pixel u = (u,v)> in the image domain u 2 U ⇢ R2 such that pk =
Rk(u)K 1 ˙u is a metric point measurement in the sensor frame o
reference k. We apply a bilateral filter [27] to the raw depth map t
obtain a discontinuity preserved depth map with reduced noise Dk
Dk(u) =
1
Wp
Â
q2U
Nss (ku qk2)Nsr (kRk(u) Rk(q)k2)Rk(q)
(2
where Ns (t) = exp( t2s 2) and Wp is a normalizing constant.
: Pixel
maps the camera coordinate frame at time k into the global frame
g, such that a point pk 2 R3 in the camera frame is transferred into
the global co-ordinate frame via pg = Tg,kpk.
We will also use a single constant camera calibration matrix
K that transforms points on the sensor plane into image pixels.
The function q = p(p) performs perspective projection of p 2
R3 = (x,y,z)> including dehomogenisation to obtain q 2 R2 =
(x/z,y/z)>. We will also use a dot notation to denote homogeneous
vectors ˙u := (u>|1)>
3.2 Surface Measurement
At time k a measurement comprises a raw depth map Rk which
provides calibrated depth measurements Rk(u) 2 R at each image
pixel u = (u,v)> in the image domain u 2 U ⇢ R2 such that pk =
Rk(u)K 1 ˙u is a metric point measurement in the sensor frame of
reference k. We apply a bilateral filter [27] to the raw depth map to
obtain a discontinuity preserved depth map with reduced noise Dk,
Dk(u) =
1
Wp
Â
q2U
Nss (ku qk2)Nsr (kRk(u) Rk(q)k2)Rk(q) ,
(2)
where Ns (t) = exp( t2s 2) and Wp is a normalizing constant.
We back-project the filtered depth values into the sensor’s frame
of reference to obtain a vertex map Vk,
central pixel to ens
aries. Subsequently
Vl2[1...L], Nl2[1...L]
corresponding dep
global co-ordinate
measurement, the
the equivalent map
N
g
k(u) = Rg,kNk(u)
3.3 Mapping as
Each consecutive d
estimate, is fused
using the volumet
[7]. In a true sign
the signed distance
face), taking on p
visible surface into
on the non-visible
ple 3D point cloud
a global frame is a
An example giv
lows us to repres
within the volume.
fusion of the regis
Sk(p) where p 2 R
R3 = (x,y,z)> including dehomogenisation to obtain q 2 R2 =
(x/z,y/z)>. We will also use a dot notation to denote homogeneous
vectors ˙u := (u>|1)>
3.2 Surface Measurement
At time k a measurement comprises a raw depth map Rk which
provides calibrated depth measurements Rk(u) 2 R at each image
pixel u = (u,v)> in the image domain u 2 U ⇢ R2 such that pk =
Rk(u)K 1 ˙u is a metric point measurement in the sensor frame of
reference k. We apply a bilateral filter [27] to the raw depth map to
obtain a discontinuity preserved depth map with reduced noise Dk,
Dk(u) =
1
Wp
Â
q2U
Nss (ku qk2)Nsr (kRk(u) Rk(q)k2)Rk(q) ,
(2)
where Ns (t) = exp( t2s 2) and Wp is a normalizing constant.
We back-project the filtered depth values into the sensor’s frame
of reference to obtain a vertex map Vk,
Vk(u) = Dk(u)K 1
˙u . (3)
Since each frame from the depth sensor is a surface measurement
on a regular grid, we compute, using a cross product between neigh-
the equivalent mappin
N
g
k(u) = Rg,kNk(u).
3.3 Mapping as S
Each consecutive dept
estimate, is fused incr
using the volumetric
[7]. In a true signed
the signed distance to
face), taking on posit
visible surface into fre
on the non-visible side
ple 3D point clouds (o
a global frame is a glo
An example given
lows us to represent
within the volume. W
fusion of the registere
Sk(p) where p 2 R3 is
reconstructed. A disc
olution is stored in gl
reside. From here on w
voxel/memory elemen
and will refer only to t
so use a dot notation to denote homogeneous
urement
ment comprises a raw depth map Rk which
pth measurements Rk(u) 2 R at each image
e image domain u 2 U ⇢ R2 such that pk =
c point measurement in the sensor frame of
a bilateral filter [27] to the raw depth map to
preserved depth map with reduced noise Dk,
(ku qk2)Nsr (kRk(u) Rk(q)k2)Rk(q) ,
(2)
t2s 2) and Wp is a normalizing constant.
e filtered depth values into the sensor’s frame
a vertex map Vk,
Vk(u) = Dk(u)K 1
˙u . (3)
m the depth sensor is a surface measurement
the equivalent mapping of norm
N
g
k(u) = Rg,kNk(u).
3.3 Mapping as Surface R
Each consecutive depth frame,
estimate, is fused incrementally
using the volumetric truncated
[7]. In a true signed distance
the signed distance to the close
face), taking on positive and i
visible surface into free space,
on the non-visible side. The res
ple 3D point clouds (or surface
a global frame is a global surfac
An example given in Figure
lows us to represent arbitrary
within the volume. We will den
fusion of the registered depth m
Sk(p) where p 2 R3 is a global
reconstructed. A discretization
olution is stored in global GPU
reside. From here on we assum
voxel/memory elements and th
: 正規化
要するに、Depthに対するBilateral Filter](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-18-320.jpg)
![Surface Measurement (3/4)
• Vertex map
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 19
Wp
Â
q2U
Nss (ku qk2)Nsr (kRk(u) Rk(q)k2)Rk(q) ,
(2)
(t) = exp( t2s 2) and Wp is a normalizing constant.
k-project the filtered depth values into the sensor’s frame
ce to obtain a vertex map Vk,
Vk(u) = Dk(u)K 1
˙u . (3)
h frame from the depth sensor is a surface measurement
ar grid, we compute, using a cross product between neigh-
a global frame is a global surfac
An example given in Figure
lows us to represent arbitrary
within the volume. We will den
fusion of the registered depth m
Sk(p) where p 2 R3 is a global
reconstructed. A discretization
olution is stored in global GPU
reside. From here on we assume
voxel/memory elements and th
and will refer only to the contin
• Normal map
De-noise後のDepth mapを使って、点 u を3次元に投影
n pro-
h data
ed into
ed dis-
ion as
local-
fused
func-
diction
using
d cur-
ses all
ame at
Figure 4: A slice through the truncated signed distance volume
showing the truncated function F > µ (white), the smooth distance
field around the surface interface F = 0 and voxels that have not yet
had a valid measurement(grey) as detailed in eqn. 9.
bouring map vertices, the corresponding normal vectors,
Nk(u) = n
⇥
(Vk(u+1,v) Vk(u,v))⇥(Vk(u,v+1) Vk(u,v))
⇤
,
(4)
where n[x] = x/kxk2.
We also define a vertex validity mask: Mk(u) 7! 1 for each pixel
where a depth measurement transforms to a valid vertex; otherwise
if a depth measurement is missing Mk(u) 7! 0. The bilateral filtered
version of the depth map greatly increases the quality of the normal
maps produced, improving the data association required in tracking
described in Section 3.5.
We compute an L = 3 level multi-scale representation of the sur-
face measurement in the form of a vertex and normal map pyramid.
First a depth map pyramid Dl2[1...L] is computed. Setting the bottom
各頂点の3次元座標から、法線を計算 (近接ピクセル3次元座標の外積)
Figure 4: A slice through the truncated signed distance volume
showing the truncated function F > µ (white), the smooth distance
field around the surface interface F = 0 and voxels that have not yet
had a valid measurement(grey) as detailed in eqn. 9.
bouring map vertices, the corresponding normal vectors,
Nk(u) = n
⇥
(Vk(u+1,v) Vk(u,v))⇥(Vk(u,v+1) Vk(u,v))
⇤
,
(4)
where n[x] = x/kxk2.
We also define a vertex validity mask: Mk(u) 7! 1 for each pixel
where a depth measurement transforms to a valid vertex; otherwise
if a depth measurement is missing Mk(u) 7! 0. The bilateral filtered
version of the depth map greatly increases the quality of the normal
maps produced, improving the data association required in tracking
described in Section 3.5.
We compute an L = 3 level multi-scale representation of the sur-
:正規化 (単位ベクトル化)](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-19-320.jpg)


![Sensor Pose Estimation (2/4)
• The global point-plane energy
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 23
(14)
ure cor-
and re-
e phys-
um and
ponding
[0.4,8]
perty of
er pixel
ed volu-
can be
ver, due
a con-
simple
kipping
a good
est sur-
n march
ave +ve
to-frame tracking is obtained simply by setting ( ˆVk 1, ˆNk 1)
(Vk 1,Nk 1) which is used in our experimental section for a com-
parison between frame-to-frame and frame-model tracking.
Utilising the surface prediction, the global point-plane energy,
under the L2 norm for the desired camera pose estimate Tg,k is:
E(Tg,k) = Â
u2U
Wk(u)6=null
⇣
Tg,k
˙Vk(u) ˆV
g
k 1 (ˆu)
⌘>
ˆN
g
k 1 (ˆu)
2
, (16)
where each global frame surface prediction is obtained using the
previous fixed pose estimate Tg,k 1. The projective data as-
sociation algorithm produces the set of vertex correspondences
{Vk(u), ˆVk 1(ˆu)|W(u) 6= null} by computing the perspectively pro-
jected point, ˆu = p(KeTk 1,k
˙Vk(u)) using an estimate for the frame-
frame transform eTz
k 1,k = T 1
g,k 1
eTz
g,k and testing the predicted and
measured vertex and normal for compatibility. A threshold on the
distance of vertices and difference in normal values suffices to re-
ject grossly incorrect correspondences, also illustrated in Figure 7:
W(u) 6= null iff
8
<
:
Mk(u) = 1, and
keTz
g,k
˙Vk(u) ˆV
g
k 1 (ˆu)k2 ed, and
heRz
g,kNk(u), ˆN
g
k 1 (ˆu)i eq .
(17)
rithm [4] to obtain correspondence and the
r pose optimisation. Second, modern GPU
y parrallelised processing pipeline, so that
point-plane optimisation can use all of the
ements.
r metric in combination with correspon-
rojective data association was first demon-
odelling system by [23] where frame-to-
(with a fixed camera) for depth map align-
instead track the current sensor frame by
easurement (Vk,Nk) against the model pre-
s frame ( ˆVk 1, ˆNk 1). We note that frame-
ained simply by setting ( ˆVk 1, ˆNk 1)
sed in our experimental section for a com-
o-frame and frame-model tracking.
prediction, the global point-plane energy,
he desired camera pose estimate Tg,k is:
g,k
˙Vk(u) ˆV
g
k 1 (ˆu)
⌘>
ˆN
g
k 1 (ˆu)
2
, (16)
e surface prediction is obtained using the
algorithm [4] to obtain correspondence and the
] for pose optimisation. Second, modern GPU
ully parrallelised processing pipeline, so that
nd point-plane optimisation can use all of the
asurements.
rror metric in combination with correspon-
g projective data association was first demon-
e modelling system by [23] where frame-to-
sed (with a fixed camera) for depth map align-
we instead track the current sensor frame by
e measurement (Vk,Nk) against the model pre-
ious frame ( ˆVk 1, ˆNk 1). We note that frame-
obtained simply by setting ( ˆVk 1, ˆNk 1)
is used in our experimental section for a com-
me-to-frame and frame-model tracking.
ce prediction, the global point-plane energy,
or the desired camera pose estimate Tg,k is:
⇣
Tg,k
˙Vk(u) ˆV
g
k 1 (ˆu)
⌘>
ˆN
g
k 1 (ˆu)
2
, (16)
ame surface prediction is obtained using the
: Live frame
: Model prediction from the previous frame
shapes in
base. For
or virtual
to form
s range
the range
planning
the ICP
st widely
a similar
Chen92]).
a recent
inal ICP
92], each
the other
oint error
between
rocess is
r it stops
2] used a
ization is
e tangent
-to-point
-to-plane
squares
Press92].
orithm is
hers have
e former
of the
Pottmann
between points in the source surface and points in the destination
surfaces. For example, for each point on the source surface, the
nearest point on the destination surface is chosen as its
correspondence [Besl92] (see [Rusinkiewicz01] for other
approaches to find point correspondences). The output of an ICP
iteration is a 3D rigid-body transformation M that transforms the
source points such that the total error between the corresponding
points, under a certain chosen error metric, is minimal.
When the point-to-plane error metric is used, the object of
minimization is the sum of the squared distance between each
source point and the tangent plane at its corresponding destination
point (see Figure 1). More specifically, if si = (six, siy, siz, 1)T
is a
source point, di = (dix, diy, diz, 1)T
is the corresponding destination
point, and ni = (nix, niy, niz, 0)T
is the unit normal vector at di, then
the goal of each ICP iteration is to find Mopt such that
( )( )∑ •−⋅=
i
iii
2
opt minarg ndsMM M (1)
where M and Mopt are 4×4 3D rigid-body transformation matrices.
Figure 1: Point-to-plane error between two surfaces.
tangent
plane
s1
source
point
destination
point
d1
n1
unit
normal
s2
d2
n2
s3
d3
n3
destination
surface
source
surface
l1
l2
l3
Low, Kok-Lim, Linear least-squares optimization for
Point-to-Plane ICP surface Registration Chapel Hill,
University of North Carolina, 2004.](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-23-320.jpg)
![Sensor Pose Estimation (3/4)
• Iterative solution
• パラメータの更新量の計算
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 24
ve value before stepping over the surface
-up obtained is demonstrated in Figure 6
of steps required for each pixel to inter-
standard marching.
ions can be obtained by solving a ray/tri-
1] that requires solving a cubic polyno-
e we use a simple approximation. Given
ntersect the SDF where F+
t and F+
t+Dt are
DF values either side of the zero crossing
nd t + Dt from its starting point, we find
where ed and eq are threshold parameters of our system. eTz=
g,
initialised with the previous frame pose Tg,k.
An iterative solution, eTz
g,k for z > 0 is obtained by minimi
the energy of a linearised version of (16) around the previous
timate eTz 1
g,k . Using the small angle assumption for an increme
transform:
eTz
inc =
h
eRz etz
i
=
2
4
1 a g tx
a 1 b ty
g b 1 tz
3
5 ,
g a surface measurement with (center) and with-
filtering applied to the raw depth map. W(u) = null
unpredicted/unmeasured points shown in white.
rm is simply eTz
g,k = eTz
inc
eTz 1
g,k . Writing the update
vector,
x = (b,g,a,tx,ty,tz)>
2 R6
(19)
urrent global frame vertex estimates for all pixels
eV
g
k(u) = eTz 1
g,k
˙Vk(u), we minimise the linearised
g the incremental point transfer:
u) = eRz eV
g
k(u)+ etz = G(u)x+ eV
g
k(u) , (20)
trix G is formed with the skew-symmetric matrix
quately constrained.
the magnitude of incr
small angle assumpt
fails, the system is pl
Relocalisation Ou
re-localisation schem
known sensor pose is
user instructed to alig
played. While runni
validity checks are pa
4 EXPERIMENTS
We have conducted a
formance of our syst
tem’s ability to keep
extensively in our su
4.1 Metrically Co
Our tracking and ma
rithm for a given are
Figure 7: Example of point-plane outliers as person steps into par-
tially reconstructed scene (left). Outliers from compatibility checks
(Equation 17) using a surface measurement with (center) and with-
out (right) bilateral filtering applied to the raw depth map. W(u) = null
are light grey with unpredicted/unmeasured points shown in white.
an updated transform is simply eTz
g,k = eTz
inc
eTz 1
g,k . Writing the update
eTz
inc as a parameter vector,
x = (b,g,a,tx,ty,tz)>
2 R6
(19)
and updating the current global frame vertex estimates for all pixels
{u|W(u) 6= null}, eV
g
k(u) = eTz 1
g,k
˙Vk(u), we minimise the linearised
error function using the incremental point transfer:
eTz
g,k
˙Vk(u) = eRz eV
g
k(u)+ etz = G(u)x+ eV
g
k(u) , (20)
can be
does no
the line
free DO
quality
a check
quately
the mag
small a
fails, th
Relo
re-loca
known
user ins
played.
validity
4 EX
We hav
forman
tem’s a
extensi
Figure 7: Example of point-plane outliers as person steps into par-
tially reconstructed scene (left). Outliers from compatibility checks
(Equation 17) using a surface measurement with (center) and with-
out (right) bilateral filtering applied to the raw depth map. W(u) = null
are light grey with unpredicted/unmeasured points shown in white.
an updated transform is simply eTz
g,k = eTz
inc
eTz 1
g,k . Writing the update
eTz
inc as a parameter vector,
x = (b,g,a,tx,ty,tz)>
2 R6
(19)
and updating the current global frame vertex estimates for all pixels
{u|W(u) 6= null}, eV
g
k(u) = eTz 1
g,k
˙Vk(u), we minimise the linearised
error function using the incremental point transfer:
eTz
g,k
˙Vk(u) = eRz eV
g
k(u)+ etz = G(u)x+ eV
g
k(u) , (20)
where the 3⇥6 matrix G is formed with the skew-symmetric matrix
form of eV
g
k(u):
G(u) =
h
eV
g
k(u)
i
⇥
I3⇥3 . (21)
An iteration is obtained by solving:
sensor motion increases the assum
of the point-plane error metric an
can be broken. Also, if the curren
does not provide point-plane pairs
the linear system then an arbitrar
free DOFs can be obtained. Both
quality reconstruction and trackin
a check on the null space of the no
quately constrained. We also perfo
the magnitude of incremental trans
small angle assumption was not d
fails, the system is placed into re-l
Relocalisation Our current imp
re-localisation scheme, whereby i
known sensor pose is used to prov
user instructed to align the incomi
played. While running the pose o
validity checks are passed tracking
4 EXPERIMENTS
We have conducted a number of ex
formance of our system. These an
tem’s ability to keep track during v
extensively in our submitted video
4.1 Metrically Consistent Re
Our tracking and mapping system
rithm for a given area of reconstr
investigating its ability to form m
trajectories containing local loop cl
global joint-estimation. We are als
system to scale gracefully with d
resources.
he 3⇥6 matrix G is formed with the skew-symmetric matrix
eV
g
k(u):
G(u) =
h
eV
g
k(u)
i
⇥
I3⇥3 . (21)
ation is obtained by solving:
min
x2R6
Â
Wk(u)6=null
kEk2
2 (22)
E = ˆN
g
k 1(ˆu)>
⇣
G(u)x+ eV
g
k(u) ˆV
g
k 1(ˆu)
⌘
(23)
mputing the derivative of the objective function with respect
parameter vector x and setting to zero, a 6 ⇥ 6 symmetric
ystem is generated for each vertex-normal element corre-
nce:
⇣ ⌘
4.1 M
Our tra
rithm f
investig
trajecto
global
system
resourc
To i
perime
ing a t
then sp
⇡ 19 s
our sys
region
tained i
a preci
easily e
x y z
and updating the current global frame vertex estimates for all pixels
{u|W(u) 6= null}, eV
g
k(u) = eTz 1
g,k
˙Vk(u), we minimise the linearised
error function using the incremental point transfer:
eTz
g,k
˙Vk(u) = eRz eV
g
k(u)+ etz = G(u)x+ eV
g
k(u) , (20)
where the 3⇥6 matrix G is formed with the skew-symmetric matrix
form of eV
g
k(u):
G(u) =
h
eV
g
k(u)
i
⇥
I3⇥3 . (21)
An iteration is obtained by solving:
min
x2R6
Â
Wk(u)6=null
kEk2
2 (22)
E = ˆN
g
k 1(ˆu)>
⇣
G(u)x+ eV
g
k(u) ˆV
g
k 1(ˆu)
⌘
(23)
By computing the derivative of the objective function with respect
to the parameter vector x and setting to zero, a 6 ⇥ 6 symmetric
linear system is generated for each vertex-normal element corre-
ICPの更新量 :
Energy Function:](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-24-320.jpg)


![DynamicFusion: Overview (1/3)
• KinectFusionをDynamicなシーンに拡張
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 28
KinectFusion: Real-Time Dense Surface Mapping and Trac
Richard A. Newcombe
Imperial College London
Shahram Izadi
Microsoft Research
Otmar Hilliges
Microsoft Research
David Molyneaux
Microsoft Research
Lancaster University
D
Micr
Newc
Andrew J. Davison
Imperial College London
Pushmeet Kohli
Microsoft Research
Jamie Shotton
Microsoft Research
Steve Hodges
Microsoft Research
Andrew
Micros
Figure 1: Example output from our system, generated in real-time with a handheld Kinect depth camera and no other sen
Normal maps (colour) and Phong-shaded renderings (greyscale) from our dense reconstruction system are shown. On the
is an example of the live, incomplete, and noisy data from the Kinect sensor (used as input to our system).
ABSTRACT
We present a system for accurate real-time mapping of complex and
arbitrary indoor scenes in variable lighting conditions, using only a
moving low-cost depth camera and commodity graphics hardware.
We fuse all of the depth data streamed from a Kinect sensor into
a single global implicit surface model of the observed scene in
real-time. The current sensor pose is simultaneously obtained by
tracking the live depth frame relative to the global model using a
coarse-to-fine iterative closest point (ICP) algorithm, which uses
all of the observed depth data available. We demonstrate the advan-
tages of tracking against the growing full surface model compared
with frame-to-frame tracking, obtaining tracking and mapping re-
sults in constant time within room sized scenes with limited drift
and high accuracy. We also show both qualitative and quantitative
1 INTRODUCTION
Real-time infrastructure-free tracking of a hand
simultaneously mapping the physical scene in h
new possibilities for augmented and mixed reali
In computer vision, research on structure fr
and multi-view stereo (MVS) has produced ma
sults, in particular accurate camera tracking and
tions (e.g. [10]), and increasingly reconstruction
(e.g. [24]). However, much of this work was not
time applications.
Research on simultaneous localisation and ma
focused more on real-time markerless tracking
construction based on the input of a single com
monocular RGB camera. Such ‘monocular SLA
MonoSLAM [8] and the more accurate Parallel](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-28-320.jpg)







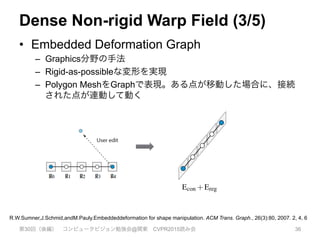
![Dense Non-rigid Warp Field (4/5)
• Dual-Quaternion Blending
– Graphics分野の手法
– 高速でアーチファクトの少ないSkinningを実現
– できるだけ体積を保存するように補間
– 2つのQuaternionを使って、回転と平行移動を表現
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 37
ns as bases and define the dense volumet-
n through interpolation. Due to its compu-
y and high quality interpolation capability
ternion blending DQB [11], to define our
xc) ⌘ SE3(DQB(xc)) , (1)
ed average over unit dual quaternion trans-
mply DQB(xc) ⌘
P
k2N (xc) wk(xc)ˆqkc
k
P
k2N (xc) wk(xc)ˆqkck
,
Wt(vc)(v>
c , 1)>
and (n
that scaling of space can
function, since compres
resented by neighbourin
diverging directions. F
out any rigid body trans
the volume, e.g., due to
troduce the explicit warp
Tlw, and compose this
(e) Canonical model warped into its live frame (f) Model Normals
online stream of noisy depth maps (a,b) and outputs a real-time dense reconstruction of the moving
mate a volumetric warp (motion) field that transforms the canonical model space into the live frame,
done, and all depth maps to be densely fused into a single rigid TSDF reconstruction (d,f). Simulta-
eld is constructed as a set of sparse 6D transformation nodes that are smoothly interpolated through
onical frame (c). The resulting per-frame warp field estimate enables the progressively denoised and
nsformed into the live frame in real-time (e). In (e) we also visualise motion trails for a sub-sample
ond of scene motion together with a coordinate frame showing the rigid body component of the scene
node to model surface distance where increased distance is mapped to a lighter value.
nd rotation results in signif-
struction. For each canoni-
transforms that point from
-rigidly deformed frame of
the warp function for each
n must be efficiently opti-
ensely sample the volume,
E(3) field at the resolution
(TSDF) geometric repre-
DF volume reconstruction
2563
voxels would require
eters per frame, about 10
with each unit dual-quaternion ˆqkc 2 R8
. Here, N (x) are
the k-nearest transformation nodes to the point x and wk :
R3
7! R defines a weight that alters the radius of influence
of each node and SE3(.) converts from quaternions back to
an SE(3) transformation matrix. The state of the warp-field
Wt at time t is defined by the values of a set of n defor-
mation nodes N t
warp = {dgv, dgw, dgse3}t. Each of the
i = 1..n nodes has a position in the canonical frame dgi
v 2
R3
, its associated transformation Tic = dgi
se3, and a ra-
dial basis weight dgw that controls the extent of the trans-
formation wi(xc) = exp kdgi
v xck2
/ 2(dgi
w)2
.
Each radius parameter dgi
w is set to ensure the node’s in-
fluence overlaps with neighbouring nodes, dependent on
the sampling sparsity of nodes, which we describe in de-
: Dual-Quaternion
L. Kavan, S. Collins, J. Zˇa ́ra, and C. O’Sullivan. Skinning with Dual Quaternions. In Proceedings of the 2007 Symposium
on Interactive 3D Graphics and Games, I3D ’07, pages 39–46, New York, NY, USA, 2007. ACM. 3
Linear Blending Dual Quaternion Blending
図は以下より転用
http://rodolphe-vaillant.fr/?e=29](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-37-320.jpg)




![Dense Non-Rigid Surface Fusion (2/3)
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 42
warped center into the depth frame. This allows the TSDF
for a point in the canonical frame to be updated by com-
puting the projective TSDF in the deforming frame without
having to resample a warped TSDF in the live frame. The
projective signed distance at the warped canonical point is:
psdf(xc) =
h
K 1
Dt (uc)
⇥
u>
c , 1
⇤>
i
z
[xt]z , (3)
where uc = ⇡ (Kxt) is the pixel into which the voxel cen-
ter projects. We compute distance along the optical (z) axis
of the camera frame using the z component denoted [.]z.
K is the known 3 ⇥ 3 camera intrinsic matrix, and ⇡ per-
forms perspective projection. For each voxel x, we update
the TSDF to incorporate the projective SDF observed in the
warped frame using TSDF fusion:
V(x)t =
(
[v0
(x), w0
(x)]>
, if psdf(dc(x)) > ⌧
V(x)t 1, otherwise
(4)
where dc(.) transforms a discrete voxel point into the con-
tinuous TSDF domain. The truncation distance ⌧ > 0 and
the updated TSDF value is given by the weighted averaging
We es
dgse3 in
current re
that is mi
E(Wt, V
Our data
cost Dat
isation te
tion fields
tween tra
The coup
transform
ularisatio
model int
enables a
when giv
sistent de
space. We
projective signed distance at the warped canonical point is:
psdf(xc) =
h
K 1
Dt (uc)
⇥
u>
c , 1
⇤>
i
z
[xt]z , (3)
where uc = ⇡ (Kxt) is the pixel into which the voxel cen-
ter projects. We compute distance along the optical (z) axis
of the camera frame using the z component denoted [.]z.
K is the known 3 ⇥ 3 camera intrinsic matrix, and ⇡ per-
forms perspective projection. For each voxel x, we update
the TSDF to incorporate the projective SDF observed in the
warped frame using TSDF fusion:
V(x)t =
(
[v0
(x), w0
(x)]>
, if psdf(dc(x)) > ⌧
V(x)t 1, otherwise
(4)
where dc(.) transforms a discrete voxel point into the con-
tinuous TSDF domain. The truncation distance ⌧ > 0 and
the updated TSDF value is given by the weighted averaging
scheme [5], with the weight truncation introduced in [18]:
v0
(x) =
v(x)t 1w(x)t 1 + min(⇢, ⌧)w(x)
w(x)t 1 + w(x)
⇢ = psdf(dc(x))
w0
(x) = min(w(x)t 1 + w(x), wmax) . (5)
Unlike the static fusion scenario where the weight w(x)
encodes the uncertainty of the depth value observed at the
projected pixel in the depth frame, we also account for un-
certainty associated with the warp function at xc. In the
E(Wt, V, Dt, E) = Data(Wt
Our data term consists of a
cost Data(Wt, V, Dt) which
isation term Reg(Wt, E) tha
tion fields, and ensures as-rigid
tween transformation nodes c
The coupling of a data-term f
transformations with a rigid-a
ularisation is a form of the e
model introduced in [25]. Th
enables a trade-off between re
when given high quality data,
sistent deformation of non or
space. We defined these terms
3.3.1 Dense Non-Rigid ICP
Our aim is to estimate all non
eters Tic and Tlw that warp t
live frame. We achieve this
rigid alignment of the curren
tracted from the canonical vol
live frame’s depth map.
Surface Prediction and Da
zero level set of the TSDF V is
and stored as a polygon mesh w
having to resample a warped TSDF in the live frame. The
projective signed distance at the warped canonical point is:
psdf(xc) =
h
K 1
Dt (uc)
⇥
u>
c , 1
⇤>
i
z
[xt]z , (3)
where uc = ⇡ (Kxt) is the pixel into which the voxel cen-
ter projects. We compute distance along the optical (z) axis
of the camera frame using the z component denoted [.]z.
K is the known 3 ⇥ 3 camera intrinsic matrix, and ⇡ per-
forms perspective projection. For each voxel x, we update
the TSDF to incorporate the projective SDF observed in the
warped frame using TSDF fusion:
V(x)t =
(
[v0
(x), w0
(x)]>
, if psdf(dc(x)) > ⌧
V(x)t 1, otherwise
(4)
where dc(.) transforms a discrete voxel point into the con-
tinuous TSDF domain. The truncation distance ⌧ > 0 and
the updated TSDF value is given by the weighted averaging
scheme [5], with the weight truncation introduced in [18]:
v0
(x) =
v(x)t 1w(x)t 1 + min(⇢, ⌧)w(x)
w(x)t 1 + w(x)
⇢ = psdf(dc(x))
w0
(x) = min(w(x)t 1 + w(x), wmax) . (5)
Unlike the static fusion scenario where the weight w(x)
encodes the uncertainty of the depth value observed at the
that is minimised by o
E(Wt, V, Dt, E) = D
Our data term consi
cost Data(Wt, V, D
isation term Reg(W
tion fields, and ensure
tween transformation
The coupling of a da
transformations with
ularisation is a form
model introduced in
enables a trade-off be
when given high qua
sistent deformation o
space. We defined the
3.3.1 Dense Non-R
Our aim is to estimat
eters Tic and Tlw tha
live frame. We achi
rigid alignment of th
tracted from the cano
live frame’s depth ma
Surface Predictio
Live FrameのProjective Signed Distance Function:
TSDFのFusion:
Truncate:](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-42-320.jpg)

![Estimating the Warp-Field State (1/5)
• Depth map Dt からdgse3を推定
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 45
DF
m-
ut
he
s:
3)
n-
xis
]z.
er-
ate
he
4)
We estimate the current values of the transformations
dgse3 in Wt given a newly observed depth map Dt and the
current reconstruction V by constructing an energy function
that is minimised by our desired parameters:
E(Wt, V, Dt, E) = Data(Wt, V, Dt) + Reg(Wt, E) . (6)
Our data term consists of a dense model-to-frame ICP
cost Data(Wt, V, Dt) which is coupled with a regular-
isation term Reg(Wt, E) that penalises non-smooth mo-
tion fields, and ensures as-rigid-as-possible deformation be-
tween transformation nodes connected by the edge set E.
The coupling of a data-term formed from linearly blended
transformations with a rigid-as-possible graph based reg-
ularisation is a form of the embedded deformation graph
model introduced in [25]. The regularisation parameter
enables a trade-off between relaxing rigidity over the field
when given high quality data, and ensuring a smooth con-
sistent deformation of non or noisily observed regions of
これを最小化する各パラメータを推定する
Energy データ項
ICP cost
正規化項
滑らかでない動き
に対するペナルティ
Wt : Warp Field
: 現在のSurface (Polygon Mesh)
Dt : Live frame Depth map
ε : Edge set (ノードの接続)
ace into the live (non-rigid) frame (see Figure 3).
hnique greatly simplifies the non-rigid reconstruc-
cess over methods where all frames are explicitly
nto a canonical frame. Furthermore, given a cor-
p field, then, since all TSDF updates are computed
stances in the camera frame, the non-rigid projec-
DF fusion approach maintains the optimality guar-
or surface reconstruction from noisy observations
y proved for the static reconstruction case in [6].
imating the Warp-field State Wt
stimate the current values of the transformations
Wt given a newly observed depth map Dt and the
econstruction V by constructing an energy function
inimised by our desired parameters:
, Dt, E) = Data(Wt, V, Dt) + Reg(Wt, E) . (6)
a term consists of a dense model-to-frame ICP
ta(Wt, V, Dt) which is coupled with a regular-](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-45-320.jpg)
![Estimating the Warp-Field State (3/5)
• ICP Cost
– Canonical Modelを現在のTでレンダリング
– Live FrameのDepth mapとのエラーをPoint-Planeで計算
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 47
transform close, modulo observation noise, to the live sur-
face vl : ⌦ 7! R3
, formed by back projection of the depth
image [vl(u)>
, 1]>
= K 1
Dt(u)[u>
, 1]>
. This can be
quantified by a per pixel dense model-to-frame point-plane
error, which we compute under the robust Tukey penalty
function data, summed over the predicted image domain
⌦:
Data(W, V, Dt) ⌘
X
u2⌦
data ˆn>
u (ˆvu vl˜u) .(7)
augment. The transformed model vertex v(u) is simply
˜Tu
= W(v(u)), producing the current canonical to live
frame point-normal predictions ˆvu = ˜Tu
v(u) and ˆnu =
˜Tu
n(u), and data-association of that model point-normal
is made with a live frame point-normal through perspective
projection into the pixel ˜u = ⇡(Kˆvu).
We note that, ignoring the negligible cost of rendering
the geometry ˆVw, the ability to extract, predict, and perform
projective data association with the currently visible canoni-
cal geometry leads to a data-term evaluation that has a com-
into v
which
assoc
insuffi
logue
in opt
How
ometr
dynam
make
it def
We
betwe
betwe
tion t
contin
larisa
Reg(
Point-Plane Error
face vl : ⌦ 7! R3
, formed by back projection of the depth
image [vl(u)>
, 1]>
= K 1
Dt(u)[u>
, 1]>
. This can be
quantified by a per pixel dense model-to-frame point-plane
error, which we compute under the robust Tukey penalty
function data, summed over the predicted image domain
⌦:
Data(W, V, Dt) ⌘
X
u2⌦
data ˆn>
u (ˆvu vl˜u) .(7)
augment. The transformed model vertex v(u) is simply
˜Tu
= W(v(u)), producing the current canonical to live
frame point-normal predictions ˆvu = ˜Tu
v(u) and ˆnu =
˜Tu
n(u), and data-association of that model point-normal
is made with a live frame point-normal through perspective
projection into the pixel ˜u = ⇡(Kˆvu).
We note that, ignoring the negligible cost of rendering
the geometry ˆVw, the ability to extract, predict, and perform
projective data association with the currently visible canoni-
cal geometry leads to a data-term evaluation that has a com-
putational complexity with an upper bound in the number
which n
associat
insuffici
logue to
in optim
How sh
ometry?
dynamic
make us
it deform
We u
between
between
tion term
continui
larisatio
Reg(W
where E
ed by back projection of the depth
K 1
Dt(u)[u>
, 1]>
. This can be
dense model-to-frame point-plane
te under the robust Tukey penalty
d over the predicted image domain
X
u2⌦
data ˆn>
u (ˆvu vl˜u) .(7)
med model vertex v(u) is simply
ucing the current canonical to live
dictions ˆvu = ˜Tu
v(u) and ˆnu =
ciation of that model point-normal
e point-normal through perspective
˜u = ⇡(Kˆvu).
ng the negligible cost of rendering
lity to extract, predict, and perform
on with the currently visible canoni-
ata-term evaluation that has a com-
associated data term. In any case,
insufficient geometric texture in t
logue to the aperture problem in o
in optimisation of the transform pa
How should we constrain the mot
ometry? Whilst the fully correct m
dynamics and, where applicable, t
make use of a simpler model of un
it deforms in a piece-wise smooth
We use a deformation graph bas
between transformation nodes, wh
between nodes i and j adds a rigi
tion term to the total error being m
continuity preserving Huber penal
larisation term sums over all pair-w
Reg(W, E) ⌘
nX
i=0
X
j2E(i)
↵ij reg
ometry should
to the live sur-
on of the depth
. This can be
me point-plane
Tukey penalty
image domain
ˆvu vl˜u) .(7)
v(u) is simply
nonical to live
(u) and ˆnu =
l point-normal
ugh perspective
st of rendering
ct, and perform
into view. However, nodes affecting canonical space within
which no currently observed surface resides will have no
associated data term. In any case, noise, missing data and
insufficient geometric texture in the live frame – an ana-
logue to the aperture problem in optical-flow – will result
in optimisation of the transform parameters being ill-posed.
How should we constrain the motion of non-observed ge-
ometry? Whilst the fully correct motion depends on object
dynamics and, where applicable, the subject’s volition, we
make use of a simpler model of unobserved geometry: that
it deforms in a piece-wise smooth way.
We use a deformation graph based regularization defined
between transformation nodes, where an edge in the graph
between nodes i and j adds a rigid-as-possible regularisa-
tion term to the total error being minimized, under the dis-
continuity preserving Huber penalty reg. The total regu-
larisation term sums over all pair-wise connected nodes:
Reg(W, E) ⌘
nX X
↵ij reg Ticdgj
Tjcdgj
, (
transform close, modulo observation noise, to the live sur-
face vl : ⌦ 7! R3
, formed by back projection of the depth
image [vl(u)>
, 1]>
= K 1
Dt(u)[u>
, 1]>
. This can be
quantified by a per pixel dense model-to-frame point-plane
error, which we compute under the robust Tukey penalty
function data, summed over the predicted image domain
⌦:
Data(W, V, Dt) ⌘
X
u2⌦
data ˆn>
u (ˆvu vl˜u) .(7)
augment. The transformed model vertex v(u) is simply
˜Tu
= W(v(u)), producing the current canonical to live
frame point-normal predictions ˆvu = ˜Tu
v(u) and ˆnu =
˜Tu
n(u), and data-association of that model point-normal
is made with a live frame point-normal through perspective
projection into the pixel ˜u = ⇡(Kˆvu).
We note that, ignoring the negligible cost of rendering
the geometry ˆVw, the ability to extract, predict, and perform
projective data association with the currently visible canoni-
Ω : ピクセルドメイン
ine. This results in a prediction of
eometry that is currently predicted
frame: P(ˆVc). We store this pre-
ages {v, n} : ⌦ 7! P(ˆVc), where
of the predicted images, storing the
me vertices and normals.
ormation parameters for the current
cted-to-be-visible geometry should
o observation noise, to the live sur-
med by back projection of the depth
K 1
Dt(u)[u>
, 1]>
. This can be
l dense model-to-frame point-plane
ute under the robust Tukey penalty
d over the predicted image domain
⌘
X
u2⌦
data ˆn>
u (ˆvu vl˜u) .(7)
med model vertex v(u) is simply
point-plane data-term evaluation
3.3.2 Warp-field Regularizat
It is crucial for our non-rigid TS
timate a deformation not only o
but over all space within S. T
of new regions of the scene surf
into view. However, nodes affec
which no currently observed su
associated data term. In any ca
insufficient geometric texture in
logue to the aperture problem i
in optimisation of the transform
How should we constrain the m
ometry? Whilst the fully correc
dynamics and, where applicable
make use of a simpler model of
it deforms in a piece-wise smoo
: robust Tukey Penalty function](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-47-320.jpg)


![Efficient Optimization
• まず、KinectFusionと同じ手順で、Camera
Pose (Tlw)を推定
• 次に、Eの最小化を行うことで、各Deformation
NodeのWarp-Fieldを求める。
• Gauss-Newton法で解く
– Gauss-Newton法: 二乗和の最小化に特化したNewton
法
– ヘッセ行列 (2階微分) をヤコビ行列 (1階微分) で近似
– コレスキー分解を使って効率的に解く
第30回(後編) コンピュータビジョン勉強会@関東 CVPR2015読み会 50
approach origi-
-rigidly deform-
t, we transform
warp into the live
arry through the
y projecting the
llows the TSDF
pdated by com-
g frame without
live frame. The
nonical point is:
[xt]z , (3)
h the voxel cen-
e optical (z) axis
ent denoted [.]z.
trix, and ⇡ per-
el x, we update
observed in the
x)) > ⌧
using distances in the camera frame, the non-rigid projec-
tive TSDF fusion approach maintains the optimality guar-
antees for surface reconstruction from noisy observations
originally proved for the static reconstruction case in [6].
3.3. Estimating the Warp-field State Wt
We estimate the current values of the transformations
dgse3 in Wt given a newly observed depth map Dt and the
current reconstruction V by constructing an energy function
that is minimised by our desired parameters:
E(Wt, V, Dt, E) = Data(Wt, V, Dt) + Reg(Wt, E) . (6)
Our data term consists of a dense model-to-frame ICP
cost Data(Wt, V, Dt) which is coupled with a regular-
isation term Reg(Wt, E) that penalises non-smooth mo-
tion fields, and ensures as-rigid-as-possible deformation be-
tween transformation nodes connected by the edge set E.
The coupling of a data-term formed from linearly blended
transformations with a rigid-as-possible graph based reg-
ularisation is a form of the embedded deformation graph
model introduced in [25]. The regularisation parameter
enables a trade-off between relaxing rigidity over the field
Energy関数 :](https://image.slidesharecdn.com/dynamicfusion-150719120213-lva1-app6891/85/30th-DynamicFusion-50-320.jpg)




