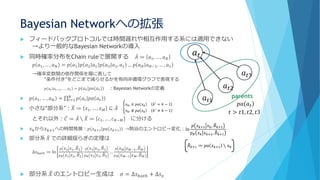
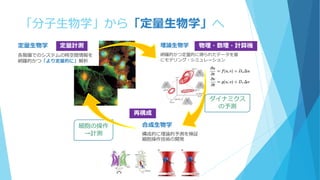
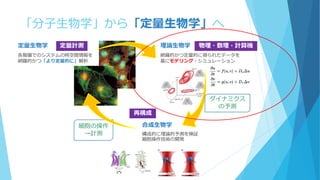
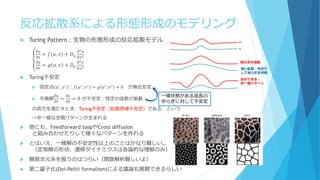
細胞現象回りの理論生物学のReviewです。以前作った「数理・物理から見た『少数性生物学』」のスライドを大幅にブラッシュアップしました。基本的にはモデリングの為の理論的な知見をまとめたという内容になっており、具体例をあまり載せていないためイメージは掴みにくいかもしれませんが、僕が持っている問題意識とそれに基づいた理論の使い分けを整理する、という観点でまとめました。「問題ごとにどういう数理を用いればよいか」という視点で全体的な概観をなんとなく掴んでもらえると嬉しいです。
前提知識としては、
①大学初年度の微積分、線形代数、微分方程式
②確率過程
③熱力学・統計力学
を知っていればだいたい読めると思います。(4つのセクションに分かれていて、それぞれは独立して読めるので、個別には全て必要ということはありませんが、①は必須です。)
※スライド15枚目と16枚目の順番が逆になってます、すみません。



















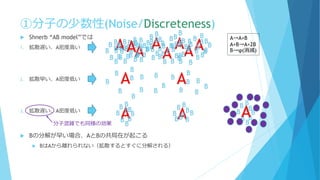
![①分子の少数性(Noise/Discreteness)
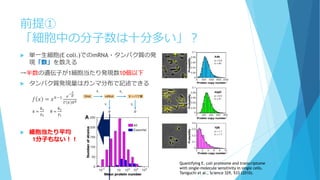
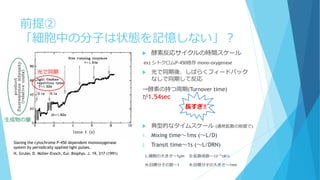
簡単な思考実験を(冨樫祐一 生体の科学 65,450 (2014))
B*B
A A*
α
α
A* B
A B*
+
+
+γ
γ
[A]total=[B]total=1
反応速度方程式は
𝑑
𝑑𝑡
𝐴∗
= α 𝐴 − γ 𝐴∗
𝐵∗
𝑑
𝑑𝑡
𝐵∗
= α 𝐵 − γ 𝐴∗
𝐵∗
α=0.0025 , γ=0.95 として定常状態は
[A]=[B]=0.95, [A*]=[B*]=0.05
一定の
確率で
活性化
ぶつかると
等しく一定の確率
でどちらかが勝つ
B*A* A×10000個
B×10000個
体積V=10000
……
……
A×10個
B×10個
体積V=10
×1000個
の容器に分割‼
………
……](https://image.slidesharecdn.com/mathphyscellphenomena-180904044920/85/slide-26-320.jpg)
![①分子の少数性(Noise/Discreteness)
数の離散性
個数∈ℕ:離散的
特に1と0(有るか無いか)の不連続な変化
A*+B*→A+B* or A*+B
は片方がなくなるともう起こらない
例えばB*がなくなると、その間A*は消費され
ないのでどんどん増える
→小分けにした箱では「A*だけ増える」or「B*
だけ増える」という状況が生じやすい
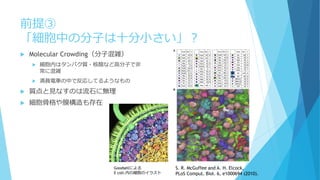
成分を連続と考えたときと比べて、
長時間平均での濃度が系のスケールに依存
して大きく変わる!!
成分が0でない実効的なネットワークのみに
注目したい
分割した場合
分
割
し
な
か
っ
た
場
合
[A*]の個数
反応速度方程式からの予想では…
濃度(個数/体積)だけで決まってほ
しい
いずれの場合も[A*]=[B*]=500個に収束
するはずだが…](https://image.slidesharecdn.com/mathphyscellphenomena-180904044920/85/slide-27-320.jpg)