xgboost를 이해하기 위해서 찾아보다가 내가 궁금한 내용을 따로 정리하였으나, 역시 구체적인 수식은 아직 모르겠다.
요즘 Kaggle에서 유명한 Xgboost가 뭘까?
Ensemble중 하나인 Boosting기법?
Ensemble 유형인 Bagging과 Boosting 차이는?
왜 Ensemble이 low bias, high variance 모델인가?
Bias 와 Variance 관계는?
Boosting 기법은 어떤게 있나?
Xgboost에서 사용하는 CART 알고리즘은?


![6
[참고] bias vs variance (1/4)
학습한 모델의 예측 오류는 크게 2개(Bias, Variance)오류로 이루어짐
Bias Variance
[ Error due to Bias ]
• Bias로 인한 에러는 예측값과 실제값 간의 차이
• (당연한 소리.. 그럼 뭐가 다른가?)
• 모델 학습시 여러 데이터를 사용하고, 반복하여 새로운 모델로 학습하면,
예측값 들의 범위를 확인 할 수 있다.
• Bias는 이 예측값 들의 범위가 정답과 얼마나 멀리 있는지 측정
http://scott.fortmann-roe.com/docs/BiasVariance.html
[ Error due to Variance ]
• 주어진 데이터로 학습한 모델이 예측한 값의 변동성 (분산, variance)
• 만약 여러 모델로 학습을 반복한다고 가정하면,
• Variance는 학습 된 모델별로 예측한 값들의 차이를 측정
Bias는 정답과 예측값의 거리
Variance는 모델별 예측값 간
의 거리](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-6-320.jpg)
![7
[참고] bias vs variance (2/4)
수학적 정의 및 예시
수학적 정의 예시 (투표 예측)
• Y : 예측 값
• X : 변수
• 𝝐 : 에러, 에러의 분포는 정규분포
• 𝐘 = 𝐟 𝐗 + 𝝐 : 예측값과 변수간의 관계 ( 𝐟 𝐗 는 정답을 추출하는 함수 )
• 𝒇4
𝐗 : 모델 학습을 통해 정답을 예측하는 함수
• 예측 모델의 에러 :
• 위 공식을 세분화하면 bias와 variance로 구성된 공식으로 변환
http://scott.fortmann-roe.com/docs/BiasVariance.html
• 목적 : 유권자들이 어떤 정당을 투표할지 예측
• 데이터 : 전화번호부에서 랜덤으로 50명 추출
• 측정 방법
• 어떤 정당에 투표할지 질문 및 결과 취합
• 여당(13), 야당(16), 무응답(21)
• [결과
• 야당이 승리 예상 à 16/(13+16)
• 실제는 여당이 압승
• 예측이 틀린 이유가 뭘까?
• Bias (전화번호부)
• 전화번호부에 있는 사용자만 대상 (특정 계층에 치우침)
• 여러가지 모델과 데이터를 샘플링해서 반복 학습해도
• 특정 계층(전화번호부에 있는)만 대변하는 결과가 추출됨.
• 단, 여러번 반복하면, variance는 낮아짐.(예측값이 서로 비슷)
• Variance (적은 샘플 데이터)
• 적은 데이터로 학습한 모델의 예측값의 차이가 큼
• 샘플을 더 많이 확보하면, variance가 줄어 듬
정답과 예측값 간의
거리 측정
예측값과 예측값 평균간의
거리
어떤 모델로도 제거 불가능한 오류.
현실 세계에서는 완벽한 모델이 없으므로, 오류가 있
다는 가정](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-7-320.jpg)
![[참고] bias vs variance (3/4)
Bias와 Variance간의 Trade-off 이해
Voter Party Registration 예측 예시
• 3개의 속성(소속정당, 자산, 종교)으로 구분된 투표자 정보
http://scott.fortmann-roe.com/docs/BiasVariance.html
• K의 갯수에 따라 예측값이 달라짐
• 빨강 : 민주당
• 파랑 : 공화당
모델
학습
학습된 모델로
신규 유권자 정당 예측
Line 위쪽은 민주당
Line 아래는 공화당
Bias vs Variance
• K 증가
• 각 에측에 더 많은 유권자 정보의 평균값 사용
• 따라서, 예측곡선이 부드러워 짐.
• K 감소
• 1인 경우, 가장 가까운 유권자 정보만 고려하여,
• 정당별로 고립되거나 급격한 예측곡선 생성됨
K=1
K=20
K=80
[Variance 관점]
• Small K è variance 증가 (모델간의 예측값 차이 큼)
• 왜 그럴까?
• 가장 가까운 값을 이용하여 예측하므로,
• 신규 데이터가 추가되면, 학습한 모델의 예측값
이 급격하게 변함 (추가된 데이터 주변)
• 따라서 모델간의 예측값 차이가 커짐
• Large K è variance 감소
• 여러 개(K)의 학습데이터를 이용하여,
• 신규 데이터 추가되도 예측값 간에 큰 변경없음
[Bias 관점]
• Small K è Bias 감소 (정답과 예측값이 유사)
• 왜 그럴까?
• 가장 가까운 값을 이용하여,
• 예측값이 정답과 근처에 있을 가능성 높음
• Large K è Bias 증가 (예측값이 정답과 많이 다름)
• 모델선형 주변으로 예측하지 못하는 데이터가
많아짐. à 예측값과 정답간의 거리가 멀어짐](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-8-320.jpg)
![9
[참고] bias vs variance (4/4)
Bias와 Variance 활용하여 모델 복잡도 최적화 하기
모델 최적화시 고려사항 Bias & Variance Trade off
[ Bias 만 줄이면 예측 정확도가 올라갈까? ]
• 많은 사람들이 Bias가 줄어야 정답을 예측할 확률이 높다고 생각한다.
• 만약 긴 시간동안 모델이 예측한 값의 평균을 생각하면 맞는 말일 것이다.
• 하지만. 실제 모델은 하나의 모델로 정확도를 평가하므로 Bias만 줄이는
것이 정확도를 높이지 못한다.
• 따라서, Bias와 Variance를 동시에 고려하여 모델 복잡도를 관리해야 함
http://scott.fortmann-roe.com/docs/BiasVariance.html
• 모델의 복잡도는 bias가 감소하고, variance가 증가하면서 발생한다.
• 따라서 모델의 복잡도가 최소화 되는 수준에서 bias와 variance를 선택
[ Bagging / Resampling의 효과]
• 위 방식은 모델 복잡도에서 variance를 줄여준다. 어떻게?
• 원본 data set에서 샘플링을 통해 여러개의 data set을 생성하고,
• 각 data set으로 모델을 학습한다.
• 이 과정에서 각 모델의 bias는 낮아지고(정답과 유사),
• variance는 높아진다. (각 모델 별로 정답의 차이가 큼)
• 그럼 어떻게 variance를 낮출까?
• Bagging에서는 각 모델의 예측값을 평균하여 예측값을 만든다.
• à 이 평균하는 과정을 통해서 각 모델간의 차이를 줄여서 variance 감소
Under Fitting Over Fitting](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-9-320.jpg)
![12
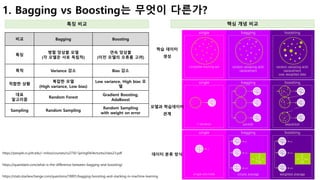
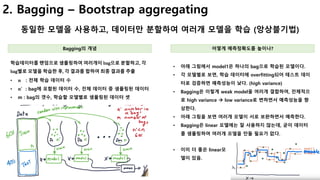
2. Random forest가 Tree correlation을 어떻게 해결하는가?
특정 feature가 정답에 많은 영향을 줄때, 모든 tree들이 비슷한 결과를 도출하는
Tree correlation문제 해결
Bagging의 이슈 Tree correlation 해결 방안
[ Random forest ]
• 데이터 샘플링 시에 일부 feature들만 랜덤으로 선택한다.
• 따라서 모든 모델들은 서로 다른 feature로 학습하게 되고, 이로 인해
tree correlation이 줄어든다.
• Bagged tree에서는 데이터를 샘플링하여 최적의 모델을 만든다. 그리고
이 과정을 n번 반복한다.
• 이렇게 만들어진 모델을 테스트 데이터로 검증하면, 당연히 서로 아주 다
른 결과가 나온다. (학습된 데이터가 서로 다르니까)
• 샘플링 된 데이터로 학습하여 high variance가 발생하는 것을 방지하기
위해서, bagging에서는 여러개의 학습모델의 결과를 합하여 최종 결과를
도출한다.
• Bagging 과정에서 한가지 이슈는 tree들이 얼마나 비슷하게 생성되는지
고려하지 못하는 것이다. (tree correlation)
• 예를 들어, 데이터 중에서 특정 변수(feature)가 정답에 미치는 영향이 아
주 커서 cost(RSS)를 많이 줄여준다고 가정하자.
• 이 feature는 모든 tree가 공유하게 되므로, 대부분의 tree에서 동일한 결
과를 예측하게 되는 현상이 발생한다. à tree correlation이 높아짐.
https://stats.stackexchange.com/questions/295868/why-is-tree-correlation-a-problem-when-
working-with-bagging
https://stats.stackexchange.com/questions/18891/bagging-boosting-and-stacking-in-machine-
learning - 모델간 비교 (자료 좋음)
http://operatingsystems.tistory.com/entry/Data-Mining-Ensemble-Bagging-and-Boosting](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-12-320.jpg)


![20
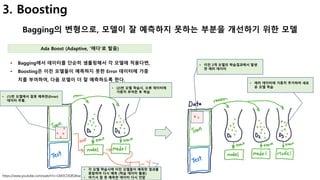
3-2. GBM(Gradient Boosting)
Gradient Boosting의 개념 및 학습 절차
https://www.analyticsvidhya.com/blog/2015/09/complete-guide-boosting-methods/
개념 고려사항
• AdaBoost과 기본 개념은 동일하고,
• 가중치(D)를 계산하는 방식에서
• Gradient Descent를 이용하여 최적의 파라미터를 찾아낸다.
• 2가지 의문점
• 정말 white noise가 아닌 error가 식별가능해?
• 만약 가능하다면, 예측 정확도가 거의 100% 가능?
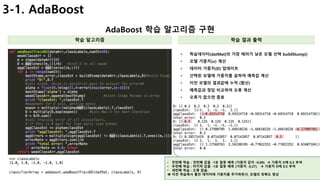
• Boosting은 과적합 가능성이 높아서, 적절한 시점에 멈춰야 함[ Easy Example ]
• Model의 예측정확도 80%인 함수
• 만약 error를 줄일 수 있다면? (error가 Y와 연관성이 있을경우)
• 정확도 84%로 증가
• 이렇게 error를 세분화하여
• 정리한 모델의 함수
• 각 함수별 최적 weight를 찾으면, 예측정확도는 더 높아짐.
• à Gradient Descent 알고리즘으로 최적 weight 계산](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-20-320.jpg)
![21
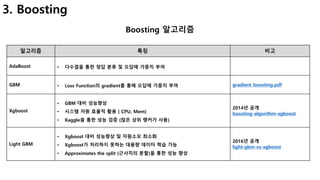
3-2. GBM(Gradient Boosting)
Gradient Boosting의 개념 및 학습 절차
Gradient Descent를 이용한 weight 계산 데이터 가중치는 어떻게 최적화하나?
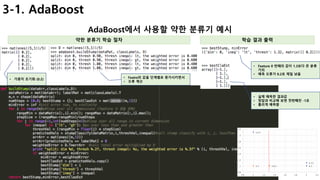
• 1번 Wezk model에서는 3개의 오분류(에러)가 발생
• 2번은 3개 에러를 제대로 분류하기 위해 가중치 부여. (다시 3개 에러 생김)
• 3번은 다시 3개 에러를 해결하기 위한 모델 생성 (다시 3개 에러 발생)
• 최적의 weight(가중치)를 찾을 때 까지 반복
[ 그럼 어떻게 가중치를 부여할까? ]
• 초기 데이터 가중치(D) = 1/n (n : 전체 학습 데이터 개수)
• 오류 (𝜺) :
오류 데이터
전체 학습 데이터
, 각 모델의 오류
• 모델의 가중치(𝜶) =
𝟏
𝟐
ln
@AB
B
• Weak model의 함수 : h(t)
• 가중치 업데이트(D) :
• 𝜶 : 는 learning rate 역할을 수행, 지수함수의
• y : 정답 (1 or -1)
• 𝒉(𝒙) : 모델의 예측값
• 𝒆𝒙𝒑함수의 인자값(𝜶 )으로 학습의 방향(최적의 weight 탐색)을 확인
• 만약 학습이 잘못 되고 있다면, −𝜶𝒚𝒊 𝒉 𝒕 𝒙𝒊
• −𝜶 ∗ 𝟏 ∗ −𝟏 = 𝜶 (정답은 1, 예측은 -1)
• −𝜶 ∗ −𝟏 ∗ 𝟏 = 𝜶 (정답은 -1, 예측은 1)
• 만약 학습이 잘되고 있으면
• −𝜶 ∗ 𝟏 ∗ 𝟏 = −𝜶 (정답은 1, 예측은 1)
• è 따라서, 예측이 틀리면 가중치(D) 증가
https://www.analyticsvidhya.com/blog/2015/09/complete-guide-boosting-methods/](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-21-320.jpg)



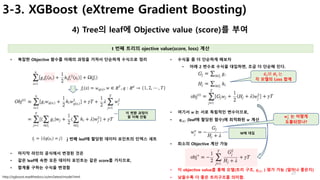
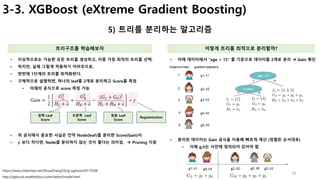





![34
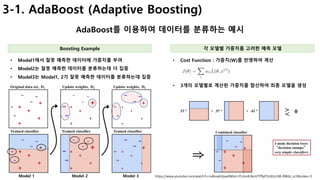
1. Decision Tree (ID3)
한번에 하나의 속성(feature)으로 데이터 분류하기
어떻게 분류 기준(속성)을 선택할까? 정보이득 계산(entropy)
• 분류하기 전과 분류 후의 변화량
• 계산값이 가장 높은 값을 선택 (변화량이 큰것)
• 모든 속성에 대하여 정보이득을 계산하여 결정
• 정보이득 계산 방법 : entropy, gini 방식
• 각 노드별로 위와 같이 정보이득 계산값으로 선택된 속성 선택
• [Entropy 방법]
• 정보에 대한 기대값 계산 공식
• 𝒍 𝒙𝒊 = 𝒑 𝒙𝒊 ∗ log 𝟐 𝒑( 𝒙𝒊)
• 𝒑 𝒙𝒊 ∶ 𝒙𝒊 항목이 선택될 확률)
• 모든 속성(feature)에 대하여 entropy값 계산하여 합산
• 𝑯 = − ∑ 𝒑 𝒙𝒊 ∗ log 𝟐 𝒑( 𝒙𝒊)𝒏
𝒊b𝟏
• n : 속성 개수
• 값이 높다는 것은 데이터가 혼잡하다는 의미.
• 속성에 있는 값이 다양하다는 의미
• 속성 값별로 count한 값
• 이 값이 크면 계산 값도 커진다
• ‘yes’ : 2 개
• ‘no’ : 3 개](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-34-320.jpg)
![35
1. Decision Tree (ID3)
모든 속성에 대하여 데이터 집합 분할하기
데이터 집합 분할 데이터 분할 예시
• Feature별로 데이터를 분할
• 아래 2개의 feature와 1개의 label(‘yes’, ’no’)
• 이를 feature에 포함된 값 별로 데이터를 분할한다.
• 예를 들어 첫번째 feature (index 0)의 값이 1인것
• [1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no']
• 제외 à [0, 1, 'no'], [0, 1, 'no']
• 이 방식으로 feature별, feature에 포함된 값 별로 데이터 분할
• 1번째 field의 값이 1인 데이터만 분할
• 0 : field의 index
• 1 : 0번째 field 값이 1인 것만 분할](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-35-320.jpg)
![36
1. Decision Tree (ID3)
데이터 분할시 가장 좋은 속성 선택하기
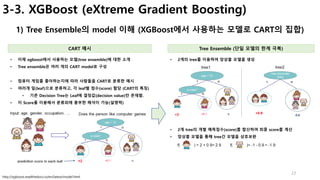
데이터 집합 분할 작업 흐름
1. 각 Feature에 포함된 값 추출 (featList)
2. featList 중복제거 à uniqueList
3. 각 feature를 속성값 기준으로 분할
4. 각 feature별 분할된 데이터의 entropy 계산
5. 원본 데이터 entropy – 분할된 데이터 entropy
• Feature별로 entropy가 계산됨
• 차이가 가장 큰 값이
• 데이터를 가장 잘 분할
6. 가장 차이가 큰 feature 선택
• 0번째 feature가 가장 데이터를 잘 분할
• 정보획득이 가장 큼
[F1 feature 분류]
• 속성 1 : YES(2), NO(1)
• 속성 0 : NO(2)
à F1으로 분류하는 것이 효과적
[F2 feature 분류]
• 속성 1 : YES(2), NO(2)
• 속성 0 : NO(1)](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-36-320.jpg)
![37
1. Decision Tree (ID3)
이제 트리를 만들어 보자 (재귀호출)
데이터 분할을 반복하여, tree를 생성 작업 흐름
1. 분류된 데이터의 label이 동일하면 중지
• classList : myDat 에서 정답(yes, no)만
추출 (['yes', 'yes', 'no', 'no', 'no'])
• 모든 정답이 동일하면 중지 (['yes', 'yes’])
2. dataSet(myDat)에 분류할 속성이 없으면 중지
• classList에 가장 많은 정답(yes or no)을
반환
3. 정보이득이 높는 속성(field) 선택
• Label 값을 함께 저장
• ['no surfacing', 'flippers']
• 선택된 label은 삭제
4. 선택된 속성의 값 별로 tree 생성
• 여기서는 ‘0’, ’1’ 별로 tree 생성
• 0인 경우 tree는 모두 ’no’
• 1인 경우 tree는 다시 최적의 속성 선택
1
2
3
4
[단점]
• 학습 데이터와 완벽히 일치 à 과적합 à 가지치기 필요
• 수치형 데이터 처리 불가 à 이산형으로 변환](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-37-320.jpg)
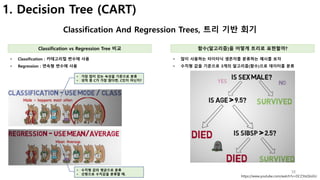

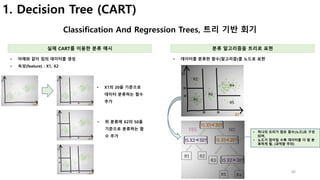

![45
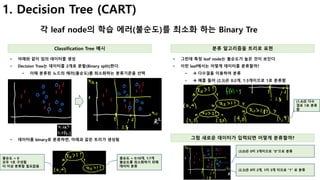
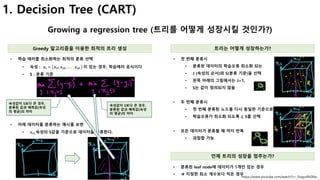
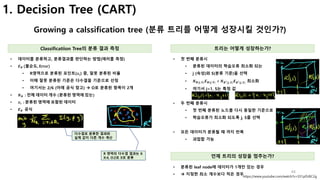
1. Decision Tree (CART, 회귀트리 모델)
연속적이고, 이산적인 속성으로 트리 구축하기
트리 생성 트리 생성 방식
• 분할에 가장 적합한 feature 선택
• 더 이상 분할할 feature가 없으면, 단말노드
• 분할 가능하면, 양쪽에 트리 생성 à 재귀호출
• Nonzero 리턴값 = 행 array, 열 array
• Array[1], array[0]의 의미는 행1, 열0 번째에
0이 아닌 값이 있다는 것
•
𝟎
𝟏
𝟎
수치형 데이터를 어떻게 분할할까?
• MSE(Mean Square Error)를 이용한 데이터 복잡성
측정
• 해당 feature 값들의 평균을 계산하고,
• 평균 제곱오류의 합으로 복잡성 측정
• à 값이 클수록 복잡함 (분류기준에 부적합)
• 코드 오류 해결
index 0 is out of bounds
for axis 0 with size 0](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-45-320.jpg)

![47
1. Decision Tree (CART, 모델트리)
회기에 의하여 트리를 선택하는 모델 (분할된 데이터 각각에 대한 선형회귀 모델)
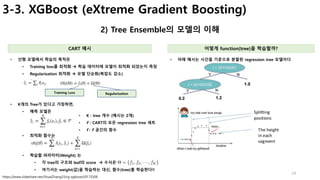
어떻게 데이터를 분할 하는가? 선형 모델 생성 및 오류 계산
• 분할된 데이터 집합의 오류를 측정
[ 어떻게 ? ]
• 분할된 데이터에 맞는 선형모델 생성
• 모델의 예측값과 정답을 비교하여 오류 계산
• modelLeaf : 데이터의 모델 가중치 파라미터 리턴
• modelErr : 모델의 예측값과 정답간의 오차를 리턴
• 기존 createTree함수를 그대로 활용
• 전달하는 파라미터(leafTyp, errTyp)만
• (modelLeaf, modelErr)로 변경하여 호출
• 회귀 트리
• 모델 트리
• chooseBestSplit 에서 분할 오류값을 측정](https://image.slidesharecdn.com/mlstudyboostingv0-171128021615/85/boosting-bagging-vs-boosting-47-320.jpg)
