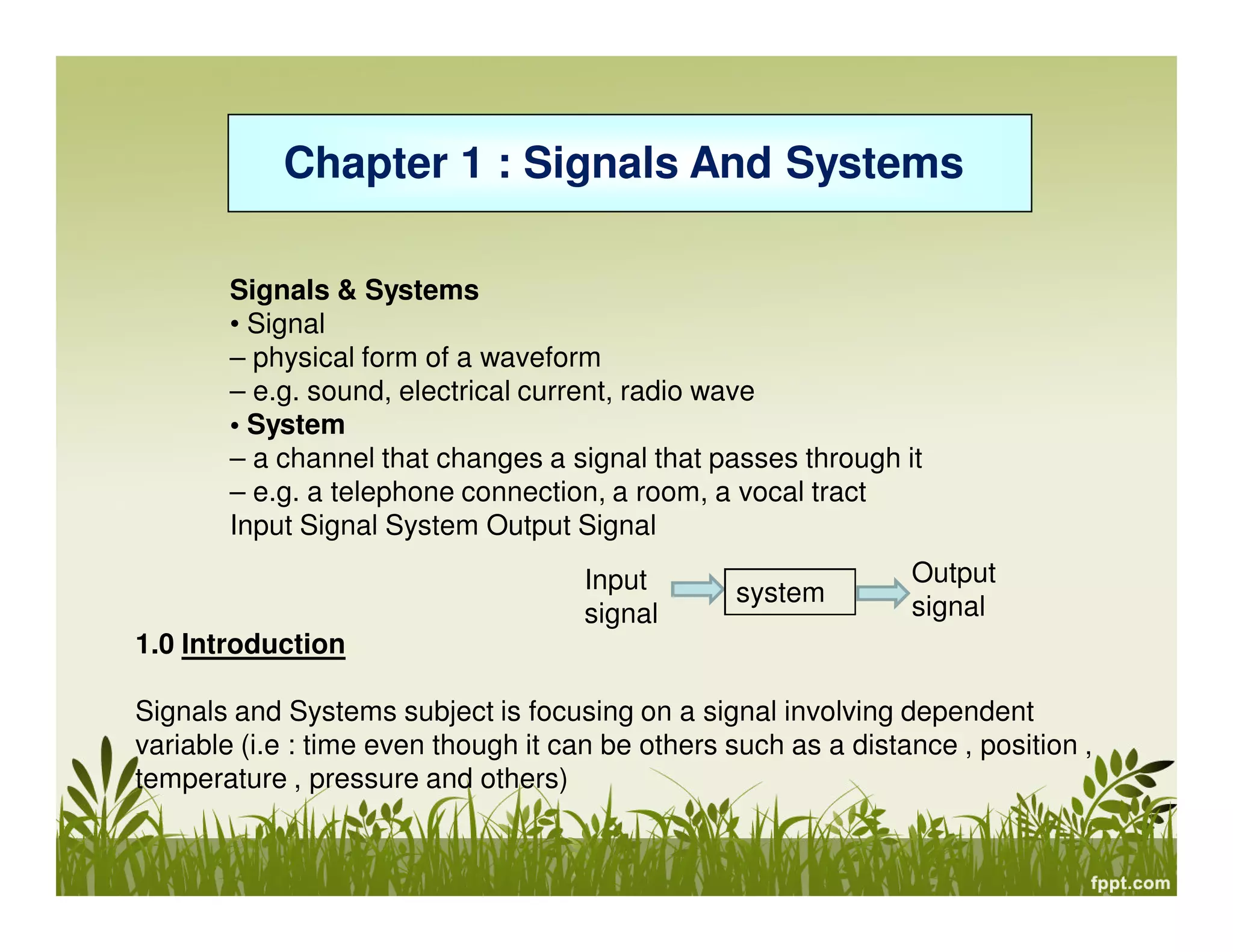
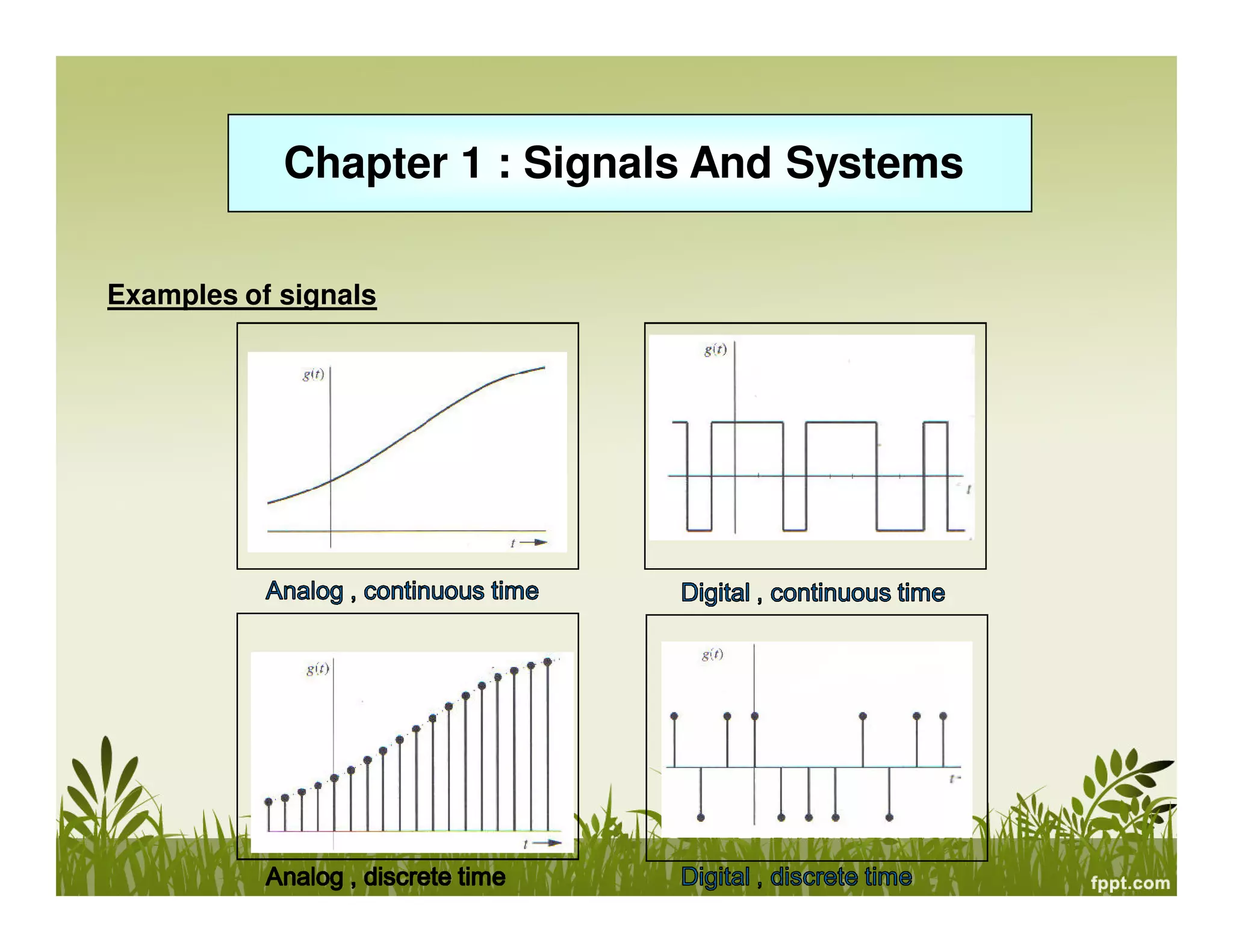
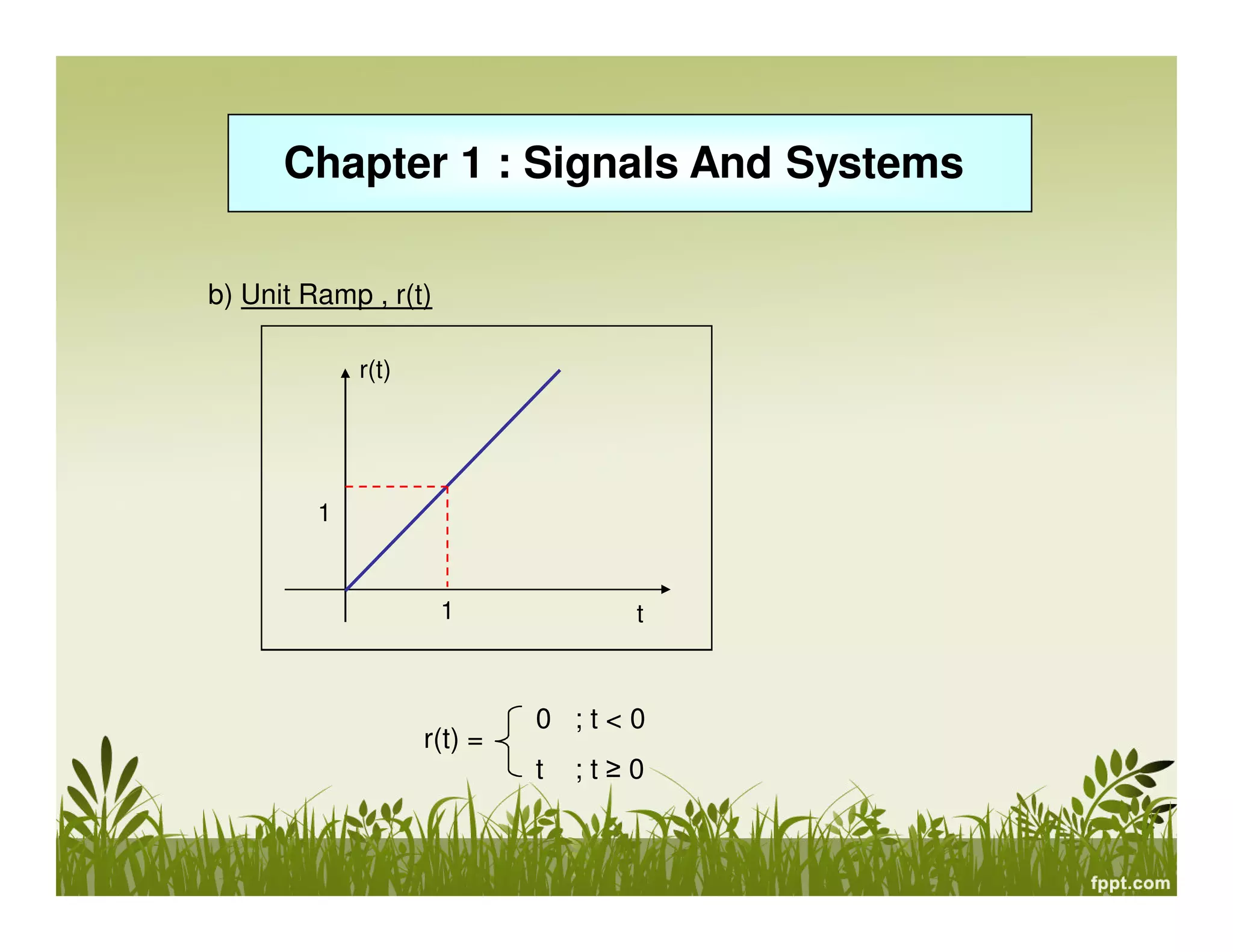
This document provides an overview of signals and systems. It defines key terms like signal, system, continuous and discrete time signals, analog and digital signals, periodic and aperiodic signals. It also discusses different types of signals like deterministic and probabilistic signals, energy and power signals. The document then classifies systems as linear/nonlinear, time-invariant/variant, causal/non-causal, and with/without memory. It provides examples of different signals and properties of signals like magnitude scaling, time shifting, reflection and scaling. Overall, the document introduces fundamental concepts in signals and systems.

1. Signals and Systems:
A computer without
signals - without
networking, audio
and video.

2. Terms
• Signal
• voltage over time
• State
• the variables of a differential equation
• System
• linear time invariant transfer function

3. Chapter 1 : Signals And Systems
Signals & Systems
• Signal
– physical form of a waveform
– e.g. sound, electrical current, radio wave
• System
– a channel that changes a signal that passes through it
– e.g. a telephone connection, a room, a vocal tract
Input Signal System Output Signal
Input
signal
system
Output
signal
1.0 Introduction
Signals and Systems subject is focusing on a signal involving dependent
variable (i.e : time even though it can be others such as a distance , position ,
temperature , pressure and others)

4. Chapter 1 : Signals And Systems
1.1 Signals and Systems
Definition
a) Signal
• A function of one/more variable which convey information on the natural of a
physical phenomenon.
• Examples : human speech, sound, light, temperature, current etc
b) Systems
• An entity that processes of manipulates one or more signals to accomplish a
function, thereby yielding new signal.
• Example: telephone connection

5. Chapter 1 : Signals And Systems
1.2 Classification of Signals
There are several classes of signals
a) Continuous time and discrete time signals
b) Analog and digital signals
c) Real and Complex signals
d) Even and Odd Signals
e) Energy and power signals
f) Periodic and aperiodic signals

6. Chapter 1 : Signals And Systems
a) Continuous time and discrete time signals
•
Continuous signals
: signal that is specified for a continuum (ALL) values
time t
: can be described mathematically by continuous
function of time as :
x(t) = A sin (ω0 t + ɸ)
where
•
A
ω
ɸ
: Amplitude
: Radian freq in rad / sec
: phase angle in rad / degree
Discrete time signals : signal that is specified only at discrete values of t

7. Chapter 1 : Signals And Systems
b) Analog and digital signals
•
Analog signals
: signal whose amplitude can take on any value in a
continuous range
•
Digital signals
: signal whose amplitude can take only a finite number
of values
(signal which associated with computer since involve
binary 1 / 0 )

8. Chapter 1 : Signals And Systems
Examples of signals

9. • Example 1:

10. • Example 2:

11. Chapter 1 : Signals And Systems
c) Deterministic and probabilistic signals
•
Deterministic signals : a signal whose physical description is known
completely either in a mathematical form or a
graphical form and its future value can be determined.
•
Probabilistic signals
: a signal whose values cannot be predicted precisely
but are known only in terms of probabilistic value such
as mean value / mean-squared value and therefore
the signal cannot be expressed in mathematical form.

12. Chapter 1 : Signals And Systems
d) Energy and power signals
•
Energy signals
: a signal with finite energy signal
•
Power signals
: a signal with finite and nonzero power
Finite energy signal
Infinite energy signal

13. Chapter 1 : Signals And Systems
1.9 Energy and Power Signals
For an arbitrary signal x(t) , the total energy , E is defined as
The average power , P is defined as

14. Chapter 1 : Signals And Systems
1.9 Energy and Power Signals
Based on the definition , the following classes of signals are defined :
a) x(t) is energy signal if and only if 0 < E < ∞ so that P = 0.
b) x(t) is a power signal if and only if 0 < P < ∞ thus implying that E = ∞.
c) Signals that satisfy neither property are therefore neither energy nor power
signals.

15. Exercise
1) Calculate the total energy of the
rectangular pulse shown in figure.
2) Given a signal as listed below, determine
whether x(t) is energy, power or neither
signal. Justify the answer.
a. x(t) = cos t
b. x(t) = 3 e-4t u(t)

16. Chapter 1 : Signals And Systems
e) Periodic and aperiodic signal
•
Periodic signals
: signal that repeats itself within a specific time or in
other words, any function that satisfies :
f (t ) = f (t + T )
where T is a constant and is called the fundamental period of the function.
T=
•
Aperiodic signals
2π
ω0
: signal that does not repeats itself and therefore does
not have the fundamental period.

17. Chapter 1 : Signals And Systems
Examples of signals
Periodic signal
Aperiodic signal

18. • Example:
Find the period for
t
f (t ) = cos
3

19. Chapter 1 : Signals And Systems
e) Periodic and aperiodic signal (continue)
•
Any continuous time signal x(t) is classified as periodic if the signal satisfies
the condition :
x(t) = x(t + nT)
•
where n = 1 , 2 , 3 ....
The sum of two or more signals is periodic if the ratio (evaluation of two
values) of their periods can be expressed as rational number. The new
fundamental period and frequency can be obtained from a periodic signal.
A rational number is a number that can be written as a simple fraction (i.e. as a ratio).
•
The sum of two or more signals is aperiodic if the ratio (evaluation of two
values) of their periods is expressed as irrational number and no new
fundamental period can be obtained.

20. • Periodic and aperiodic signal
(continue)
x(t) = x(t + nT)
Tο = 2π / ωο
π
Ωο = m
2π
N
π

21. Chapter 1 : Signals And Systems
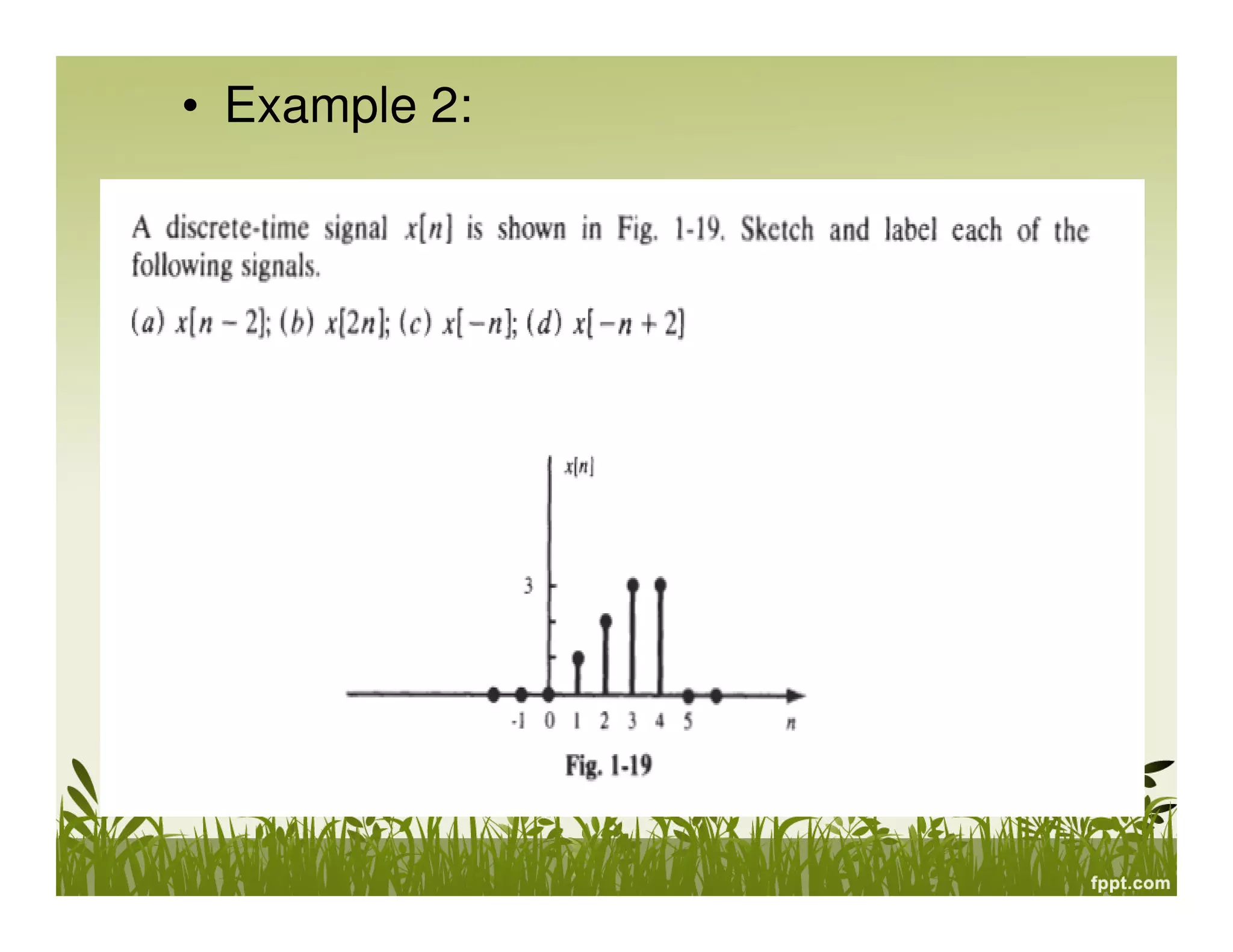
Exercise 1
•
Determine whether listed x(t) below is periodic or aperiodic signal. If a signal is
periodic, determine its fundamental period.
T=
a) x(t) = sin 3t
b) x(t) = 2 cos 8πt
c) x(t) = 3 cos (5πt + π/2)
d) x(t) = cos t + sin √2 t
e) x(t) = sin2t
j[(π/2)t-1]
f) x(t) = e
2π
ω0

22. EXERCISE 2
a)
b)
c)
d)
j(π/4)n
x[n]=e
x[n]=cos1/4n
x[n]= cos π/3 n + sin π/4n
x[n]=cos2π/8n

23. Chapter 1 : Signals And Systems
Exercise 2
•
Determine whether the following signals are periodic or aperiodic. Find the
new fundamental period if necessary.
a) x3(t) = 6 x1(t) + 2 x2(t)
b) x5(t) = 6 x1(t) + 2 x2(t) + x4(t)
where :
x1(t) = sin 13t
x2(t) = 5 sin (3000t + π/4)
x4(t) = 2 cos (600πt – π/3)

24. Chapter 1 : Signals And Systems
Exercise 3
•
Given x1(t) = 2 sin (5t) , x2(t) = 5 sin (3t) and x3(t) = 5 sin (2t + 25o) .
•
If x(t) = x1(t) – 3x2(t) + 2x3(t) , determine whether x(t) is periodic or aperiodic
signal .
•
If it is periodic, determine it’s period and frequency

25. Chapter 1 : Signals And Systems
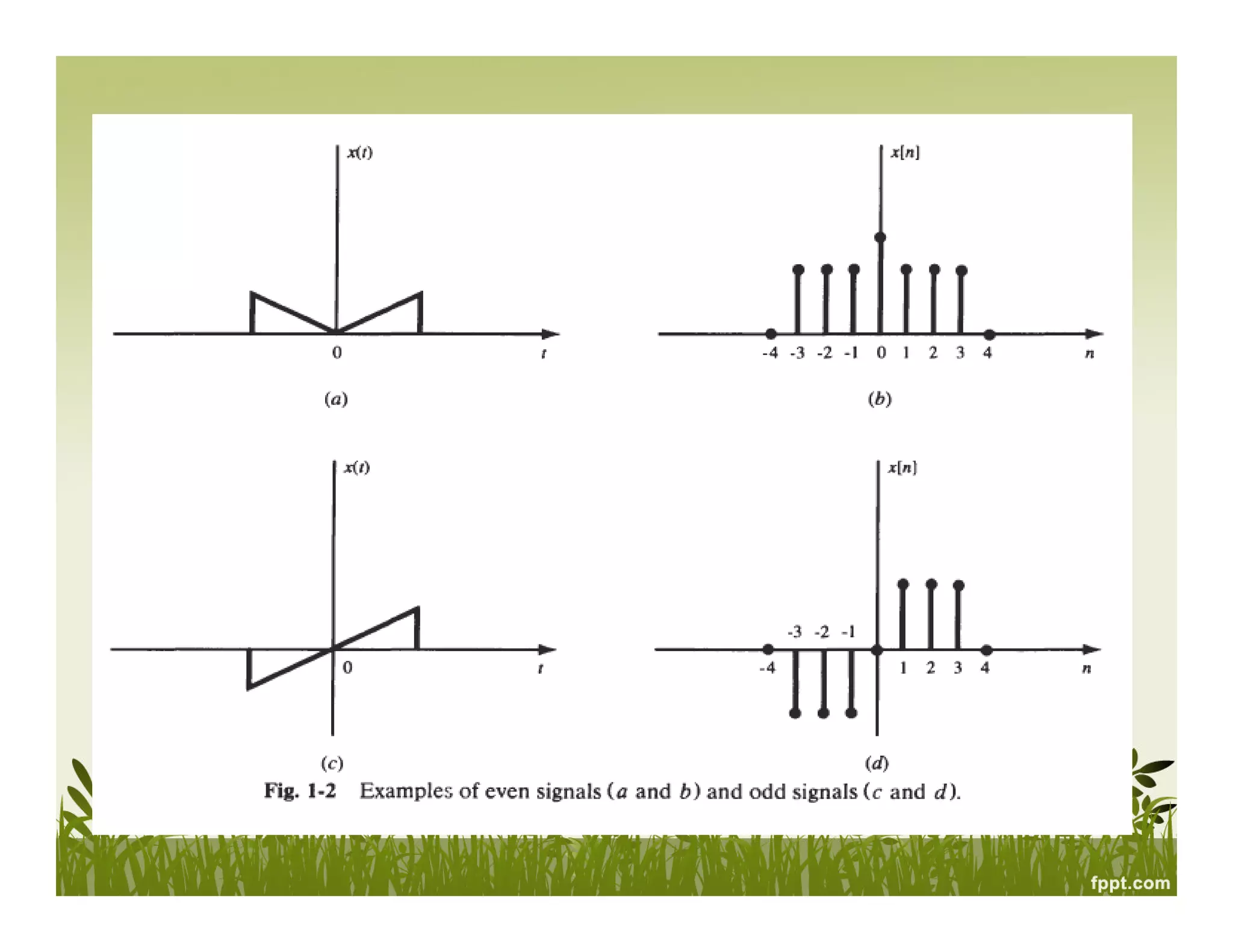
• Even and Odd
A signal x ( t ) or x[n] is referred to as an even signal if
x(-t)=x(r)
x[-n]=x[n]
A signal x ( t ) or x[n] is referred to as an odd signal if
x(-t)=-x(t)
x[-n]=-x[n]
Examples of even and odd signals are shown in Fig. 1-2.

27. Chapter 1 : Signals And Systems
1.4) Singularity Functions
is an important and unique sub-class of aperiodic signals
they are either discontinuous or continuous derivatives
they are basic signals to represent other signals
a) Unit Step, u(t)
u(t)
u(t) =
1
t
0 ;t<0
1 ;t≥0

28. Chapter 1 : Signals And Systems
b) Unit Ramp , r(t)
r(t)
1
1
r(t) =
t
0 ;t<0
t
;t≥0

29. Chapter 1 : Signals And Systems
c) Unit impulse, δ(t)
δ(t)
δ(t) =
1
t
1 ;t=0
0 ;t≠0

31. 1.5) Representation of Signals
A deterministic signal can be represented in
terms of:
1. sum of singularity functions
2. sum of steps functions and
3. piece-wise continuous functions

32. Chapter 1 : Signals And Systems
Sum Of Singularity Function
Express signal in term of sum of singularity function
Note : the ramp function r(t) can be described by step function as :
r(t)
= t u(t)
r(t±a)
= (t±a) u(t±a)
Example
Express the following signal in term of sum of singularity function.
x(t)
Answer
x(t) = u(t+1) – r(t+1) + r(t-1) + u(t-1)
1
= u(t+1) – (t+1)u(t+1) + (t-1)u(t-1) + u(t-1)
1
-1
-1
t

33. Chapter 1 : Signals And Systems
Exercise
Express the following signals in term of sum of singularity function.
x(t)
Answer
1
1
2
3
4
t
x(t)= r(t) – 2r(t-1) + 2r(t+3) +r(t-4)
= r(t) – 2(t-1)u(t-1) +2(t+3)u(t+3) +(t-4)u(t-4)
-1
x(t)
2
Answer
1
-2
-1
1
2
t
x(t) = 2δ(t+2) - u(t+2) + r(t+1) – r(t-1) – u(t-1) + δ(t+2)

34. Chapter 1 : Signals And Systems
Exercise
Sketch the following signal if the sum of singularity function of the signal is given as :
a) x(t) = r(t) + r (t-1) - u (t-1)
b)
y(t) = u(t+1)-r(t+1)+r(t-1)+u(t-1)
c) x(t) = r(t) + r(t+1) + 2u(t+1) – r(t+1) + 2r(t) – r(t-1) + u(t-2) – 2u(t-3)

35. Chapter 1 : Signals And Systems
Piece – wise continous function
Description of signal from a general form of y = mx + c
Example
Given the signal x(t) as shown below , express the signals x(t) in terms of piece
wise continuous function
x(t)
Solution
1
-1
0
1
2
t
x(t) =
-t-1
t
1
0
; -1 < t < 0
;0<t<1
;1<t<2
; elsewhere

36. Chapter 1 : Signals And Systems
Exercise
Example
Given the signal x(t) as shown below , express the signals x(t) in terms of piece
wise continuous function .
x(t)
1
1
-1
0
2
t

37. Chapter 1 : Signals And Systems
Exercise
Example
Given the signal x(t) as shown below , express the signals x(t) in terms of piece
wise continuous function .
x(t)
Solution
1
1
-1
0
2
t
x(t) =
t+1
-1
0
; -1 < t < 0
;1<t<2
; elsewhere

38. Chapter 1 : Signals And Systems
1.6 Properties of Signals
There are 4 properties of signals
a) Magnitude scaling
b) Time reflection
c) Time scaling
d) Time shifting

39. Chapter 1 : Signals And Systems
a) Magnitude scaling : Any arbitrary real constant is multiplied to a signal and
the result is, for a unit step the amplitude changes, for a unit ramp, the slope
changes and for a unit impulse, the area changes
A
-A
A
3
slope = 2
t
t
3u(t)
-2
t
1
-2u(t)
A
2r(t)
A
t
2
0
3
A
-0.5
slope = -2
-2
-2r(t)
0
3δ(t)
t
-0.5δ(t)
t

40. Chapter 1 : Signals And Systems
b) Time reflection : The mirror image of the signal with respect to the y-axis
u(t)
δ(t)
r(t)
1
1
0
u(-t)
t
slope = -1
t
r(-t)
0
δ(-t)
t

41. Chapter 1 : Signals And Systems
c) Time scaling : The expansion or compression of the signal with
respect to time t axis
x(0.5t)
a
x(kt)
a
2b
b
t
t
x(2t)
x(kt)
a
k > 1 compression
k < 1 expansion
0.5b
x(2t)
t

42. Chapter 1 : Signals And Systems
f) Time shifting : The shifting of the signal with respect to the x - axis
u(t)
u(t)
r(t)
1
1
slope = 1
t
1
u(t-1)
t
-1
u(t+1)
r(t)
r(t-1)
δ(t)
-2
3
t
r(t+1)
2
0
3δ(t-2)
t
-0.5
slope = 1
-1
t
1
t
-0.5δ(t+2)

43. Chapter 1 : Signals And Systems
Example 1
Given the signal x(t) as shown below , sketch y(t) = 3x (1- t/2) .
x(t)
1
t
-1
0
1
2

44. Chapter 1 : Signals And Systems
Example 2
Given the signal x(t) as shown below , sketch y(t) = 2x (-0.5t+1) using both
graphical and analytical method.
x(t)
1
-1
t
1
-1
2

45. Chapter 1 : Signals And Systems
Exercise
Given the signal x(t) as shown below , sketch y(t) = -2x (2-0.5t) + 1
using both graphical and analytical method.
x(t)
1
t
-2
1
-1
-1
2
3

46. Chapter 1 : Signals And Systems
1.9 Energy and Power Signals
For an arbitrary signal x(t) , the total energy , E is defined as
The average power , P is defined as

47. Chapter 1 : Signals And Systems
1.9 Energy and Power Signals
Based on the definition , the following classes of signals are defined :
a) x(t) is energy signal if and only if 0 < E < ∞ so that P = 0.
b) x(t) is a power signal if and only if 0 < P < ∞ thus implying that E = ∞.
c) Signals that satisfy neither property are therefore neither energy nor power
signals.

48. Chapter 1 : Signals And Systems
2.0 Classification Of System
i) a) With memory(dynamic)
b) Without memory(static)
ii) a) Causal
: the present output depends on past
and/or future input.
: the present output depends only on
present input.
: the output does not depends on future but can
depends on the past or the present input..
b) Non-causal
: the output depends on future input

49. Chapter 1 : Signals And Systems
2.0 Classification Of System
iii) a) Time variant
: y2 (t) ≠ y1 (t- to)
: same input produces different output at different time
b) Time invariant
: y2 (t) = y1 (t- to)
: same input produces same output at different time
where :
y1 (t- to) is the output corresponding to the time shifting , (t- to) at y1 (t)
y2(t) is the output corresponding to the input x2(t) where x2(t) = x1 (t- to)

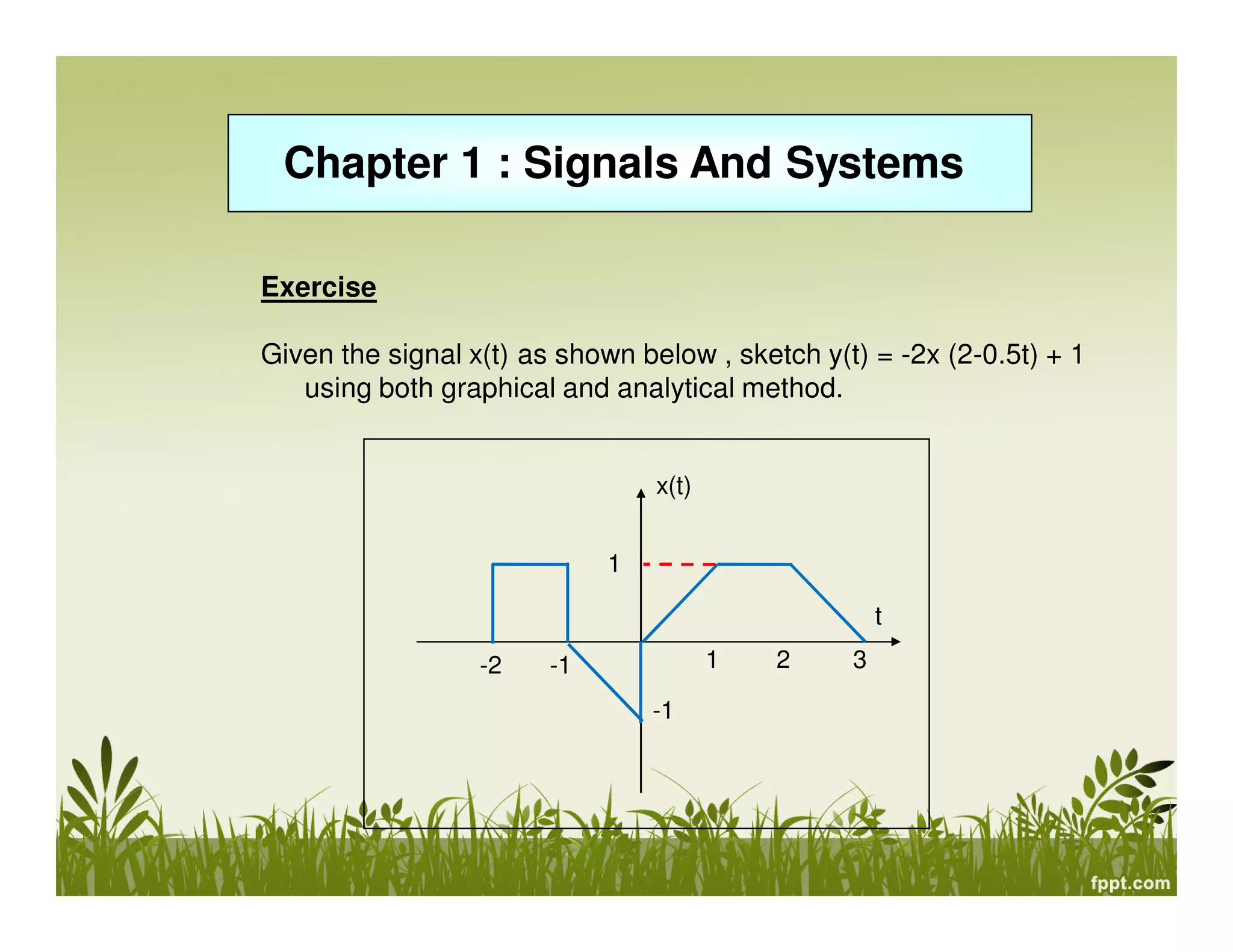
50. Chapter 1 : Signals And Systems
2.0 Classification Of System
4) a) Linear
: y(t) = ay1(t) + by2(t) (superposition applied)
b) Non linear : y(t) ≠ ay1(t) + by2(t) (superposition not applied )
where :
If an excitation x1[t] causes a response y1[t] and an excitation x2 [t] causes a
response y2[n] , then an excitation :
x [t = ax1[t] + bx2[t]
will cause the response
y [t] = ay1[t] + by2[t]
(to be presented as y(t) in solution)

51. Chapter 1 : Signals And Systems
Example
The following system is defined by the input – output relationship where x(t) is the
input and y(t) is the output.
a) y(t) = 10x2 (t+1)
e) y’(t) + y(t) = x(t)
b) y(t) = 10x(t) + 5
f) y’(t) + 10y(t) + 5 = x(t)
c) y(t) = cos (t) x(t) + 5
g) y’(t) + 3y(t) = x(t) + 2x2(t)
Determine whether the system is :
i.
Static or dynamic
ii.
Causal or non-causal
iii. Time - variant or time invariant
iv. Linear or non-linear