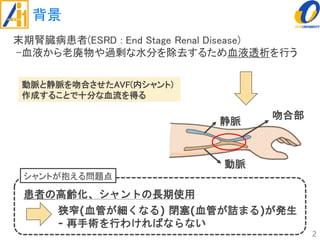
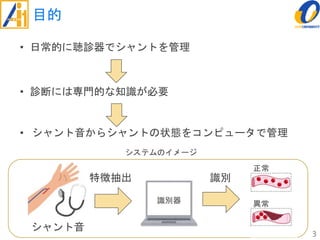
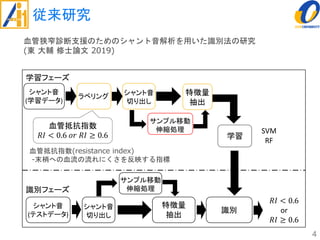
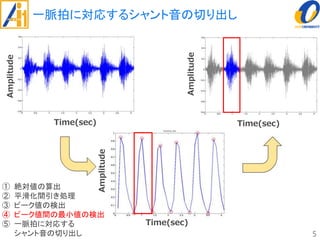
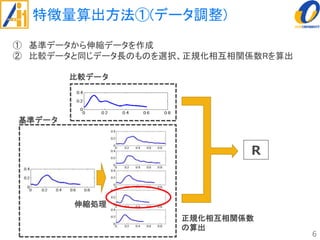
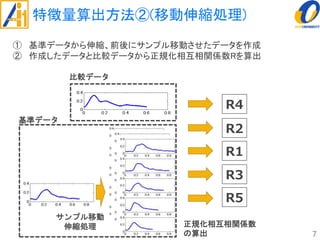
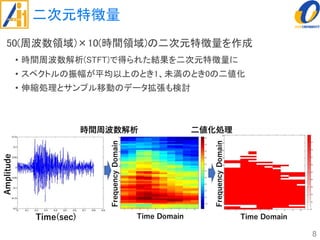
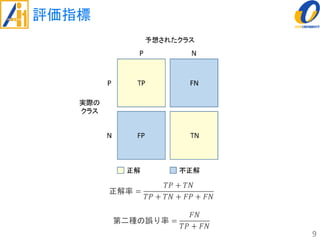
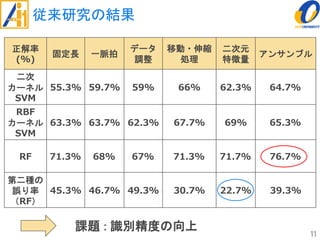
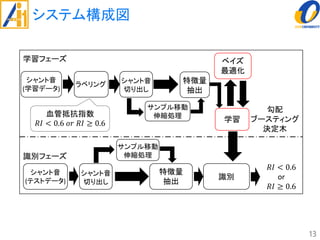
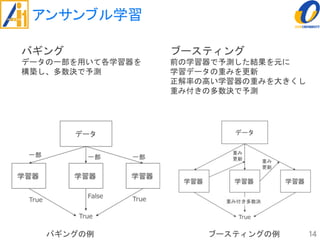
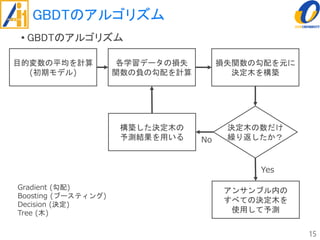
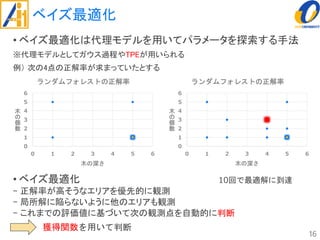
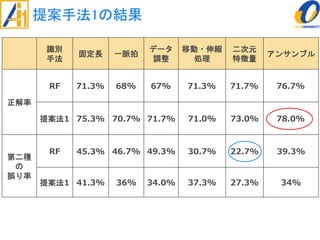
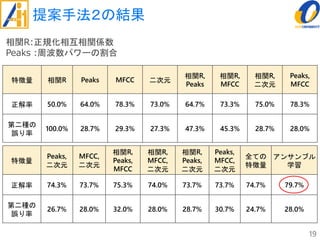
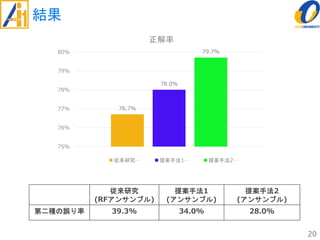
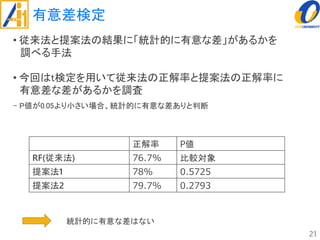
The document describes a study on improving the accuracy of detecting blood vessel stenosis using phonocardiograms. The study proposes using gradient boosting decision trees instead of random forests for classification, and exploring different combinations of four frequency-domain features extracted from phonocardiograms. Experiments show the proposed method achieves higher accuracy rates and lower false negative rates than previous methods, demonstrating its effectiveness in identifying normal and abnormal blood vessels from heart sound data.