More Related Content
PDF
PPTX
DXとかDevOpsとかのなんかいい感じのやつ 富士通TechLive PDF
多人数不完全情報ゲームにおけるAI ~ポーカーと麻雀を例として~ PDF
モデルアーキテクチャ観点からのDeep Neural Network高速化 PPTX
Ponanzaにおける強化学習とディープラーニングの応用 PDF
PPTX
Swin Transformer (ICCV'21 Best Paper) を完璧に理解する資料 PDF
What's hot
PDF
PDF
深層学習による自然言語処理入門: word2vecからBERT, GPT-3まで PDF
大規模ソーシャルゲーム開発から学んだPHP&MySQL実践テクニック PDF
PDF
「NVIDIA プロファイラを用いたPyTorch学習最適化手法のご紹介(修正版)」 PDF
PDF
[part 2]ナレッジグラフ推論チャレンジ・Tech Live! PDF
[DL輪読会]A Bayesian Perspective on Generalization and Stochastic Gradient Descent PPTX
PPTX
PPTX
[DL輪読会]Focal Loss for Dense Object Detection PPTX
PPTX
【DL輪読会】言語以外でのTransformerのまとめ (ViT, Perceiver, Frozen Pretrained Transformer etc) PDF
PPTX
PPTX
PPTX
深層学習を用いたコンピュータビジョン技術とスマートショップの実現 PPTX
PPTX
PPTX
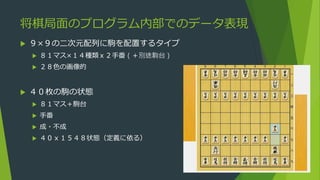
[DL輪読会]Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets 深層学習の将棋Aiへの浸透について
- 1.
- 2.
- 3.
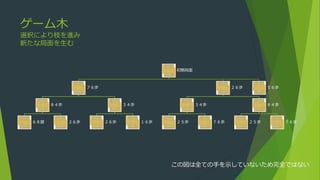
二人零和有限確定完全情報ゲーム
二人
プレイヤー数
零和(ゼロサム)
対戦者の利得の総和が0である
有限
局面状態数が有限数である(駒数および升数が有限数のため組み合わせも有限)
確定
さいころやルーレットのような確率的な遷移過程ではない
完全情報
互いのプレイヤーに与えられていない情報がない。情報の均衡
将棋・囲碁・オセロ・チェス・連珠など多くの二人テーブルゲームが含まれる
- 4.
- 5.
探索の種類
Min-Max法
具体的な計算手法にアルファベータ法など
評価値が間違っていなければ探索範囲内では必ず最善手となるが,探索前に評価値を決
定する必要がある
手が進んだ先の局面から探索をはじめる
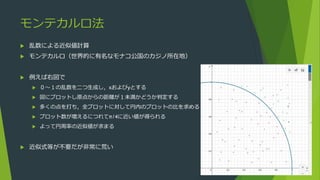
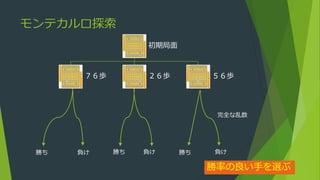
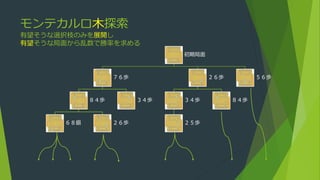
モンテカルロ探索
発展形にモンテカルロ木探索など
評価しづらい局面であっても探索は可能(原理的には勝敗判定のみで動作する)
現局面から探索をはじめる
二人零和有限確定完全情報ゲームに限らない
- 6.
- 7.
- 8.
- 9.
モンテカルロ木探索(Monte Carlo treesearch)
基本原理は古いが,Rémi Coulomにより2006年命名・実証された
囲碁AI Crazy Stone
精度の低いモンテカルロ探索をベースに桁違いのパフォーマンスで有望な手を発見可能
大きなブレイクスルー!!
以後,大きな発展のベースに
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.