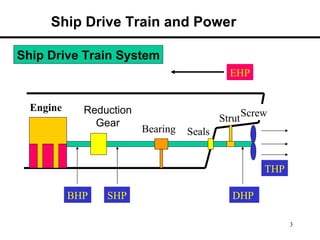
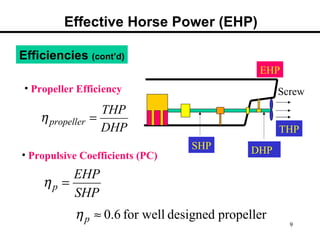
1. The document discusses the various components of ship resistance including viscous resistance, wave-making resistance, and air resistance. 2. Viscous resistance is affected by factors like Reynolds number and hull shape, with slender hulls reducing the normal component. 3. Wave-making resistance drastically increases above the hull speed as transverse wave length approaches ship length. Bulbous bows can reduce bow wave resistance. 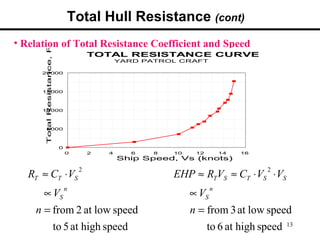4. Total resistance is calculated from coefficients of viscous, wave-making, and air resistance, with model tests needed to determine wave-making coefficient.

1. 1

2. Chap 7 Resistance and Powering of Ship
Objectives
• Prediction of Ship’s Power
- Ship’s driving system and concept of power
- Resistance of ship and its components
· frictional resistance
· wave-making resistance
· others
- Froude expansion
- Effective horse power calculation
• Propeller Theory
- Propeller components and definitions
- Propeller theory 2
- Cavitation

3. Ship Drive Train and Power
Ship Drive Train System
EHP
Engine Reduction
Gear Strut Screw
Bearing Seals
THP
BHP SHP DHP
3

4. Ship Drive Train and Power
Horse Power in Drive Train
Brake Horse Power (BHP)
- Power output at the shaft coming out of the engine before
the reduction gears
Shaft Horse Power (SHP)
- Power output after the reduction gears
- SHP=BHP - losses in reduction gear
4

5. Ship Drive Train and Power
Delivered Horse Power (DHP)
- Power delivered to the propeller
- DHP=SHP – losses in shafting, shaft bearings and seals
Thrust Horse Power (THP)
- Power created by the screw/propeller
- THP=DHP – Propeller losses
BHP SHP DHP THP EHP
E/G R/G Shaft Prop. Hull
Bearing
Relative Magnitudes
BHP>SHP>DHP>THP>EHP 5

6. Effective Horse Power (EHP)
• EHP : The power required to move the ship hull at a given
speed in the absence of propeller action
(EHP is not related with Power Train System)
• EHP can be determined from the towing tank experiments at
the various speeds of the model ship.
• EHP of the model ship is converted into EHP of the full scale
ship by Froude’s Law.
Measured EHP
V
Towing Tank Towing carriage
6

7. Effective Horse Power (EHP)
Effective Horsepower, EHP (HP)
POWER CURVE
YARD PATROL CRAFT
1000
800
600
400
200
0
0 2 4 6 8 10 12 14 16
Ship Speed, Vs (Knots)
Typical EHP Curve of YP 7

8. Effective Horse Power (EHP)
Efficiencies
• Hull Efficiency
EHP
ηH =
THP
- Hull efficiency changes due to hull-propeller interactions.
- Well-designed ship : η H  1
- Poorly-designed ship : η H 1
Well-designed
- Flow is not smooth.
- THP is reduced.
Poorly-designed
- High THP is needed
8
to get designed speed.

9. Effective Horse Power (EHP)
Efficiencies (cont’d)
EHP
• Propeller Efficiency Screw
THP
η propeller =
DHP THP
SHP DHP
• Propulsive Coefficients (PC)
EHP
ηp =
SHP
η p ≈ 0.6 for well designed propeller
9

10. Total Hull Resistance
• Total Hull Resistance (RT)
The force that the ship experiences opposite to the motion of
the ship as it moves.
• EHP Calculation
 ft 
RT (lb) ⋅ VS  
EHP(H P ) = s RT = total hull resistance
 ft lb 
550 sH   VS = speed of ship
 P 
 ft  lb ⋅ ft J
RT ⋅V S ⇒ ( lb ) ⋅   = = = Watts : Power
 s  s s
1 Watts = 1 / 550 H P 10

11. Total Hull Resistance (cont)
• Coefficient of Total Hull Resistance
- Non-dimensional value of total resistance
RT lb
CT = ⇒ 2
⇐ non - dimension
0.5ρ Vs S
2
 lb ⋅ s 2  ft  2
 4 
   ft

 ft  s 
CT = Coefficient of total hull resistance in calm water
RT = Total hull resistance
ρ = Fluid density
VS = Speed of ship
S = wetted surface area on the submerged hull 11

12. Total Hull Resistance (cont)
• Coefficient of Total Hull Resistance (cont’d)
-Total Resistance of full scale ship can be determined using
CT , ρ , S and VS
2
RT (lb) = 0.5ρSVS ⋅ CT
CT : determined by the model test
ρ : available from water property table
S : obtained from Curves of form
VS : Full scale ship speed
12

13. Total Hull Resistance (cont)
Total Resistance, Rt (lb)
• Relation of Total Resistance Coefficient and Speed
TOTAL RESISTANCE CURVE
YARD PATROL CRAFT
20000
15000
10000
5000
0
0 2 4 6 8 10 12 14 16
Ship Speed, Vs (knots)
2 2
RT ≈ CT ⋅ VS EHP ≈ RTVS ≈ CT ⋅ VS ⋅ VS
n n
∝ VS ∝ VS
n = from 2 at low speed n = from 3 at low speed
to 5 at high speed to 6 at high speed 13

14. Components of Total Resistance
• Total Resistance
R = R + R + RA
T V W
RV : Viscous Resistance
RW : Wave Making Resistance
RA : Air Resistance
• Viscous Resistance
- Resistance due to the viscous stresses that the fluid exerts
on the hull.
( due to friction of the water against the surface of the ship)
- Viscosity, ship’s velocity, wetted surface area of ship
generally affect the viscous resistance. 14

15. Components of Total Resistance
• Wave-Making Resistance
- Resistance caused by waves generated by the motion of the ship
- Wave-making resistance is affected by beam to length ratio,
displacement, shape of hull, Froude number (ship length &
speed)
• Air Resistance
- Resistance caused by the flow of air over the ship with no
wind present
- Air resistance is affected by projected area, shape of the ship
above the water line, wind velocity and direction
- Typically 4 ~ 8 % of the total resistance
15

16. Components of Total Hull Resistance
• Total Resistance and Relative Magnitude of Components
Air Resistance
Resistance (lb)
Hollow
Hump Wave-making
Viscous
Speed (kts)
- Low speed : Viscous R
- Higher speed : Wave-making R
- Hump (Hollow) : location is function of ship length and speed.
16

17. Why is a Golf Ball Dimpled?
• Let’s look at a Baseball (because that’s what I have
numbers for)
– At the velocities of 50 to 130 mph dominant in baseball the air
passes over a smooth ball in a highly resistant flow.
– Turbulent flow does not occur until nearly 200 mph for a smooth
ball
– A rough ball (say one with raised stitches like a baseball) induces
turbulent flow
– A baseball batted 400 feet would only travel 300 feet if it was
smooth.
– A non-dimpled golf ball would really hamper Tiger Woods’ long 17
game

18. Coefficient of Viscous Resistance
• Viscous Flow around a ship
Real ship : Turbulent flow exists near the bow.
Model ship : Studs or sand strips are attached at the bow
to create the turbulent flow. 18

19. Coefficient of Viscous Resistance (cont)
• Coefficients of Viscous Resistance
- Non-dimensional quantity of viscous resistance
- It consists of tangential and normal components.
CV = Ctangential Cnormal= CF + KCF
al
+
orm
al
g e nti
flow
n
bow tan ship stern
• Tangential Component : CF
- Tangential stress is parallel to ship’s hull and causes
a net force opposing the motion ; Skin Friction
- It is assumed CF can be obtained from the experimental
data of flat plate.
19

20. Coefficient of Viscous Resistance (cont)
Tangential Component of CV = CF
0.075
CF = Semi-empirical
(log10 Rn − 2) 2 equation
LVS
Rn =
ν
Rn = Reynolds Number
L = L pp (ft)
VS = Ship Speed(ft/s)
ν = Kinematic Viscosity (ft 2 /s)
= 1.2260 × 10 -5 ft 2 /s forfresh
water
20
= 1.2791 × 10 ft /s for salt
-5 2
water

21. Coefficient of Viscous Resistance (cont)
• Tangential Component (cont’d)
- Relation between viscous flow and Reynolds number
· Laminar flow : In laminar flow, the fluid flows in layers
in an orderly fashion. The layers do not mix transversely
but slide over one another.
· Turbulent flow : In turbulent flow, the flow is chaotic and
mixed transversely.
Flow over
flat plate
Laminar Flow Turbulent Flow
Rn < about × 10
5 5 Rn > about × 1021
5 5

22. Coefficient of Viscous Resistance (cont)
• Normal Component
- Normal component causes a pressure distribution along the
underwater hull form of ship
- A high pressure is formed in the forward direction opposing
the motion and a lower pressure is formed aft.
- Normal component generates the eddy behind the hull.
- It is affected by hull shape.
Fuller shape ship has larger normal component than slender
ship. large eddy
Full ship
Slender ship
small eddy
22

23. Coefficient of Viscous Resistance (cont)
• Normal Component (cont’d)
- It is calculated by the product of Skin Friction with Form Factor.
Normal Component of Cv = K CF
CF = Skin Friction Coeff.
K = Form Factor
2
 ∇(ft ) 3
B ( ft ) 
K = 19 
 L( ft ) B ( ft )T ( ft ) L( ft ) 
 
23

24. Summary of Viscous Resistance Coefficient
CV = Ctangential Cnormal= CF + K CF
+
0.075  ∇(ft )3
B ( ft ) 
2
CF = 2 K = 19 
 L( ft ) B ( ft )T ( ft ) L( ft ) 
(log10 Rn − 2)  
LVS
Rn = K= Form Factor
ν
Rn = Reynolds Number
L = L pp (ft)
VS = Ship Speed(ft/s)
ν = Kinematic Viscosity (ft 2 /s)
= 1.2260 × 10-5 ft 2 /s forfresh
water
24
= 1.2791 × 10-5 ft 2 /s for salt
water

25. Summary of Viscous Resistance Coefficient
• Reducing the Viscous Resistance Coeff.
- Method :
Increase L while keeping the submerged volume constant
1) Form Factor K ↓ ⇒ Normal component KCF ↓
∴ Slender hull is favorable. ( Slender hull form will create
a smaller pressure difference between bow and stern.)
2) Reynolds No. Rn ↑ ⇒ CF ↓ ⇒ KCF ↓
25

26. Wave-Making Resistance
Typical Wave Pattern
Stern divergent wave Bow divergent wave
L
Transverse wave Wave Length
26

27. 27

28. Wave-Making Resistance
Transverse wave System
• It travels at approximately the same speed as the ship.
• At slow speed, several crests exist along the ship length
because the wave lengths are smaller than the ship length.
• As the ship speeds up, the length of the transverse wave
increases.
• When the transverse wave length approaches the ship length,
the wave making resistance increases very rapidly.
This is the main reason for the dramatic increase in
Total Resistance as speed increases.
28

29. Wave-Making Resistance (cont)
Transverse wave System
Vs < Hull Speed
Slow
Speed
Wave
Length
Vs ≈ Hull Speed High
Speed
Wave Length
Hull Speed : speed at which the transverse wave length equals
the ship length. 29
(Wavemaking resistance drastically increases above hull speed)

30. Wave-Making Resistance (cont)
Divergent Wave System
• It consists of Bow and Stern Waves.
• Interaction of the bow and stern waves create the Hollow or
Hump on the resistance curve.
• Hump : When the bow and stern waves are in phase,
the crests are added up so that larger divergent wave systems
are generated.
• Hollow : When the bow and stern waves are out of phase,
the crests matches the trough so that smaller divergent wave
systems are generated. 30

31. Wave-Making Resistance (cont)
Calculation of Wave-Making Resistance Coeff.
• Wave-making resistance is affected by
- beam to length ratio
- displacement
- hull shape
- Froude number
• The calculation of the coefficient is far difficult and inaccurate
from any theoretical or empirical equation.
(Because mathematical modeling of the flow around ship
is very complex since there exists fluid-air boundary,
wave-body interaction)
• Therefore model test in the towing tank and Froude expansion
31
are needed to calculate the Cw of the real ship.

32. Wave-Making Resistance (cont)
Reducing Wave Making Resistance
1) Increasing ship length to reduce the transverse wave
- Hull speed will increase.
- Therefore increment of wave-making resistance of longer
ship will be small until the ship reaches to the hull speed.
- EX :
FFG7 : ship length 408 ft Which ship requires more
hull speed 27 KTS horse power at 35 KTS?
CVN65 : ship length 1040 ft
hull speed 43 KTS
32

33. Wave-Making Resistance (cont)
Reducing Wave Making Resistance (cont’d)
2) Attaching Bulbous Bow to reduce the bow divergent wave
- Bulbous bow generates the second bow waves .
- Then the waves interact with the bow wave resulting in
ideally no waves, practically smaller bow divergent waves.
- EX :
DDG 51 : 7 % reduction in fuel consumption at cruise speed
3% reduction at max speed.
design &retrofit cost : less than $30 million
life cycle fuel cost saving for all the ship : $250 mil.
33
Tankers & Containers : adopting the Bulbous bow

34. Wave-Making Resistance (cont)
Bulbous Bow
34

35. Coefficient of Total Resistance
Coefficient of total hull resistance
CT = CV + CW + C A
= C F ( 1 + K) + CW + C A
C A: Correlation Allowance
Correlation Allowance
• It accounts for hull resistance due to surface roughness,
paint roughness, corrosion, and fouling of the hull surface.
• It is only used when a full-scale ship prediction of EHP is made
from model test results.
• For model, C A = 0 Since model surface is smooth.
• For ship, empirical formulas can be used.
35

36. Other Type of Resistances
• Appendage Resistance
- Frictional resistance caused by the underwater appendages
such as rudder, propeller shaft, bilge keels and struts
- 2∼24% of the total resistance in naval ship.
• Steering Resistance
- Resistance caused by the rudder motion.
- Small in warships but troublesome in sail boats
•Added Resistance
- Resistance due to sea waves which will cause the ship
motions (pitching, rolling, heaving, yawing).
36

37. Other Resistances
• Increased Resistance in Shallow Water
- Resistance caused by shallow water effect
- Flow velocities under the hull increases in shallow water.
: Increment of frictional resistance due to the velocities
: Pressure drop, suction, increment of wetted surface area
→ Increases frictional resistance
- The waves created in shallow water take more energy from
the ship than they do in deep water for the same speed.
→ Increases wave making resistance
37

38. Basic Theory Behind Ship Modeling
• Modeling a ship
- It is not possible to measure the resistance of the full-scale ship
- The ship needs to be scaled down to test in the tank but
the scaled ship (model) must behave in exactly same way
as the real ship.
- How do we scale the prototype ship ?
- Geometric and Dynamic similarity must be achieved.
prototype ship
?
model ship
prototype Dimension Model
Speed 38
Force

39. Basic Theory behind Ship Modeling
• Geometric Similarity
- Geometric similarity exists between model and
prototype if the ratios of all characteristic dimensions
in model and prototype are equal.
- The ratio of the ship length to the model length is typically
used to define the scale factor.
Scale Factor = λ
LS (ft) S : full scale ship
λ= : Length
LM (ft)
M : Model
2 S S (ft 2 )
λ = : Area
S M (ft 2 )
3 ∇ S (ft 3 )
λ = : Volume
∇ M (ft 3 ) 39

40. Basic Theory behind Ship Modeling
• Dynamic Similarity
- Dynamic Similarity exists between model and prototype
if the ratios of all forces in model and prototype are the
same.
- Total Resistance : Frictional Resistance+ Wave Making+Others
CV = f ( Rn ), CW = f ( Fn )
RnS = RnM , FnS = FnM
LSVS LMVM VS VM
= , =
vS vM gLS gLM
vM LS LM
VM = VS , VM = VS
vS LM LS
40

41. Basic Theory behind Ship Modeling
• Dynamic Similarity (cont’d)
- Both Geometric and Dynamic similarity cannot be achieved
at same time in the model test because making both Rn and
Fn the same for the model and ship is not physically possible.
Example
Ship Length=100ft, Ship Speed=10kts, Model Length=10ft
Model speed to satisfy both geometric and dynamic similitude?
LM vM LS
VM = VS VM = VS
LS vS LM
10 ft 100 ft
= 10( kts ) = 10( kts ) (assume vM = vS )
100 ft 10 ft
41
= 1( kts ) = 100( kts )

42. Basic Theory behind Ship Modeling
• Dynamic Similarity (cont’d)
- Choice ?
· Make Fn the same for the model.
· Have Rn different
⇒ Incomplete dynamic similarity
- However partial dynamic similarity can be achieved by
towing the model at the “corresponding speed”
- Due to the partial dynamic similarity, the following
relations in forces are established.
CWM = CWS
CVM ≠ CVS 42

43. Basic Theory behind Ship Modeling
• Corresponding Speeds
VS VM
FnS = FnM , =
gLS gLM
VS (ft/s) VM (ft/s)
=
LS (ft) LM (ft)
- Example :
Ship length = 200 ft, Model length : 10 ft
Ship speed = 20 kts, Model speed towed ?
LM 1 1kt.=1.688 ft/s
VM = VS = VS
LS LS / LM
1 1
= VS = 20kts = 4.47 kts
λ
43
20

44. Basic Theory behind Ship Modeling
• Modeling Summary
CT = CV + CW + C A = CF (1 + K ) + CW + C A
1) CTM = CFM (1 + K M ) + CWM + C AM Measured in tank
Froude CWM = CTM −CFM (1 + K ) − C AM
Expansion
2) CTS = CFS (1 + K S ) + CWS + C AS
3) RTS ⋅ VS
EHP ( hp ) = ( RTS = CTS * 0.5ρ S S SVs 2 )
550
CWS = CWM ( FnS = FnM , VS / gLS = VM / gLM )
C FM , CFS (calculate d)
KS = KM ( due to scale factor λ. Calculated or given )
C AM = 0 ( Model is smooth)
44
C AS ≠ 0 (given, or calculated)