HarmonicOscillator

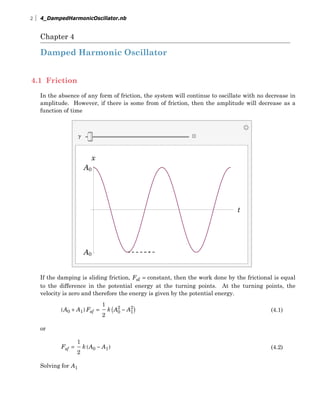
1. Chapter 4
Damped Harmonic Oscillator
4.1 Friction
In the absence of any form of friction, the system will continue to oscillate with no decrease in
amplitude. However, if there is some from of friction, then the amplitude will decrease as a
function of time
g
t
A0
A0
x
If the damping is sliding friction, Fsf = constant, then the work done by the frictional is equal
to the difference in the potential energy at the turning points. At the turning points, the
velocity is zero and therefore the energy is given by the potential energy.
(4.1)HA0 + A1L Fsf =
1
2
k IA0
2
- A1
2
M
or
(4.2)Fsf =
1
2
k HA0 - A1L
Solving for A1
2 4_DampedHarmonicOscillator.nb

2. (4.3)A1 = A0 -
2 Fsf
k
damping coefficient
2 4 6 8 10
-1.0
-0.5
0.5
1.0
4.2 Velocity Dependent Friction
Another common form of friction is proportional to the velocity of the object. This includes, air
drag (at low velocities), viscous drag and magnetic drag.
Formally, the frictional force points in the opposite direction to the velocity
(4.4)Ff = -b v
4_DampedHarmonicOscillator.nb 3

3. t
1
The total force on the mass is then F = -k x - b v. Therefore the equation of motion becomes
(4.5)F = m
d2 x
d t2
= -k x - b
d x
d t
or
(4.6)m
d2 x
d t2
+ b
d x
d t
+ k x = 0
Let’s try our previous trick to find the energy. Multiply the equation by v and rewrite
d2 x
d t2
=
d v
d t
(4.7)m v
d v
d t
+ b v2
+ k v x = 0
or
(4.8)m v
d v
d t
+ k x
d x
d t
= -b v2
The quantity on the left hand side is just the time rate of change of the energy
(4.9)
d
m v2
2
+
k x2
2
d t
=
d E
d t
= -b v2
Previously we had b = 0 and consequently the energy was a constant in time. Now we see that
4 4_DampedHarmonicOscillator.nb

4. d E
d t
< 0 i.e. the energy decreases with time. To estimate the rate of the decrease of E, we can
rewrite the above equation as
(4.10)
d E
d t
= -
2 b
m
1
2
m v2
and replace both sides of the equation by the average value of the quanties. This is not pre-
cisely correct as we are neglecting some terms.
(4.11)
d E
d t
= -
2 b
m
m v2
2
= -
2 b
m
E
2
= -
b
m
E
where we have used the fact that for the undamped harmonic oscillator
1
2
m v2 =
E
2
. Now we
can solve the equation
(4.12)E = E0 ‰
-
b t
m = E0 ‰-t g
= E0 ‰
-
t
t
The average energy decreases exponentially with a characteristic time t = 1 ê g where g = b ê m.
From this equation, we see that the energy will fall by 1 ê ‰ of its initial value in time t
g
1êg
t
E0
‰
E0
x
For an undamped harmonic oscillator,
1
2
k x2 =
E
2
. Therefor one would expect that
4_DampedHarmonicOscillator.nb 5

5. (4.13)x ∂ E ∂ ‰
-
1
2
g t
4.3 Formal Solution
Dividing Equation 4.6 by m, we have that
(4.14)
d2 x
d t2
+
b
m
d x
d t
+
k
m
x =
d2 x
d t2
+ g
d x
d t
+ w0
2 x = 0
Substitute a solution of the form A ‰Â w t
(4.15)
-A ‰Â t w
w2
+  A ‰Â t w
g w + w0
2
A ‰Â t w
= 0
A ‰Â t w I g w - w2 + w0
2M = 0
Because ‰Â w t ∫ 0 or A ∫ 0, A ‰Â w t will be a solution if
(4.16)-Â g w + w2 - w0
2 = 0
or
(4.17)
w1 =
1
2
 g + -g2
+ 4 w0
2
w2 =
1
2
 g - -g2
+ 4 w0
2
The complete solution then is
(4.18)
x@tD = A1 ‰Â t w1 + A2 ‰Â t w2
= A1 ‰
-
t g
2
+
1
2
 t -g2+4 w
0
2
+ A2 ‰
-
t g
2
-
1
2
 t -g2+4 w
0
2
4.3.1 No Damping g = 0
For b = 0, we obtain our previous solution
(4.19)x@tD = A1 ‰Â t w0 + A2 ‰- t w0
For intial condition at t = 0, x@0D = x0 and v@0D = v0, we have that
6 4_DampedHarmonicOscillator.nb

6. (4.20)
x@0D = A1 + A2 = x0
v@0D = Â A1 w0 - Â A2 w0 = v0
Solving for A1 and A2, we obtain
(4.21)
A1 =
x0
2
-
 v0
2 w0
A2 =
x0
2
+
 v0
2 w0
Clearly A1 is the complex conjugate of A2. Rewritting them in exponential form
(4.22)
A1 =
v0
2 + x0
2 w0
2
2 w0
‰-Â f
=
1
2
x0
2
+
v0
2
w0
2
‰-Â f
A2 =
v0
2 + x0
2 w0
2
2 w0
‰Â f
=
1
2
x0
2
+
v0
2
w0
2
‰Â f
where Tan@fD =
v0
x0 w0
The displacement then becomes
(4.23)
x@tD = A1 ‰Â t w0 + A2 ‰- t w0 =
v0
2 + x0
2 w0
2
2 w0
‰Â f- t w0 + ‰- f+ t w0
=
Cos@f - t w0D v0
2 + x0
2 w0
2
w0
4.3.2 Small Damping
g
2
< w0
For
g
2
< w0, the term in the exponent, 4 w0
2
- g2
will be real. Defining a new frequency,
wD =
1
2
4 w0
2
- g2
= w0
2
-
g2
4
, we obtain
4_DampedHarmonicOscillator.nb 7

7. (4.24)
x@tD = A1 ‰-
t g
2
+
1
2
 t -g2
+4 w0
2
+ A2 ‰-
t g
2
-
1
2
 t -g2
+4 w0
2
= ‰-
t g
2 IA1 ‰Â t wD
+ A2 ‰-Â t wD
M
We can now identify wD as the frequency of oscillations of the damped harmonic oscillator. As
before we can rewrite the exponentials in terms of Cosine function with an arbitrary phase.
(4.25)x@tD = A ‰
-
t g
2 Cos@wD t - fD
For intial condition at t = 0, x@0D = x0 and v@0D = v0, we have that
(4.26)
x@0D = A Cos@fD = x0
v@0D = -
1
2
A g Cos@fD + A Sin@fD wD = v0
Substituting, for Cos[f] from the first equation into the second, we have that
(4.27)-
g x0
2
+ A Sin@fD wD = v0
Therefore
(4.28)
A Cos@fD = x0
A Sin@fD =
2 v0 + g x0
2 wD
Solving for A and f
(4.29)
A = x0
2
+
H2 v0 + g x0L2
4 wD
2
Tan@fD =
2 v0 + g x0
2 x0 wD
One can check this answer by taking the limit as g Ø 0 (no damping), wD Ø w0 and the expres-
sions for A and f should reduce to our previous result.
(4.30)
A = x0
2 +
v0
2
w0
2
Tan@fD =
v0
x0 w0
8 4_DampedHarmonicOscillator.nb

8. g
2
w
7.5 3.5
q0 q
°
0
1.22 0
2 4 6 8 10
-1.0
-0.5
0.5
1.0
initial angle HradiansL
initial angular velocity
4.3.3 Critical Damping
g
2
= w0
At
g
2
= w0, the frequency wD vanishes and the expression in the exponent reduces to
(4.31)-
g
2
≤
1
2
 -g2
+ 4 w0
2
Ø -
g
2
The solution no longer has an oscillatory part. In addition one no longer has two solutions
that can be used to fit arbitrary initial conditions.
The general solution as a function of time becomes
(4.32)x@tD = ‰
-
t g
2 HA + B tL
The second term is necessary to satisfy all possible initial conditions. Differentiating
(4.33)
v@tD = -
1
2
‰
-
t g
2 HA g + B H-2 + t gLL
a@tD =
1
4
‰
-
t g
2 g HA g + B H-4 + t gLL
4_DampedHarmonicOscillator.nb 9

9. Substituting in the differential equation
(4.34)
d2 x
d t2
+ g
d x
d t
+ w0
2
x = 0
1
4
‰
-
t g
2 g HA g + B H-4 + t gLL + -
1
2
‰
-
t g
2 g HA g + B H-2 + t gLL + w0
2
‰
-
t g
2 HA + B t
-
1
4
‰
-
t g
2 HA + B tL Ig2 - 4 w0
2M = 0
which by the definition, g2 = 4 w0
2, is identically equal to zero
To determine A and B from the initial conditions, equate
(4.35)
x@0D = ‰
-
t g
2 HA + B tL
t=0
= A
v@tD = -
1
2
‰
-
t g
2 HA g + B H-2 + t gLL
t=0
=
1
2
H2 B - A gL
Solving for A and B
(4.36)
A = x0
B =
1
2
H2 v0 + g x0L
and therefore the general solution becomes
(4.37)x@tD = ‰
-
t g
2 x0 +
1
2
t H2 v0 + g x0L
4.3.4 Overdamping
g
2
> w0
For
g
2
> w0, the argument of the square root becomes negative. Taking the -1 out of the
squareroot so that its argument is now positive, the frequency, w, becomes completely
imaginary
(4.38)
w1 =
 g
2
+ -
g2
4
+ w0
2 ->
 g
2
+ Â
g2
4
- w0
2
w1 =
 g
2
- -
g2
4
+ w0
2
->
 g
2
- Â
g2
4
- w0
2
10 4_DampedHarmonicOscillator.nb

10. Again, there are no oscillatory terms. Both solutions are dying exponentials
(4.39)
x@tD = A1 ‰
t -
g
2
-
g2
4
-w
0
2
+ A2 ‰
t -
g
2
+
g2
4
-w
0
2
Although the second term contains a growing exponential,
gD
2
= J
g
2
N
2
- w0
2 <
g
2
and so the
overal function is still a dying exponential.
As before, to determine A1 and A2 from the initial conditions, equate
(4.40)x@0D = ‰
t J-
g
2
-
gD
2
N
A1 + ‰
t J-
g
2
+
gD
2
N
A2
t=0
= A1 + A2
and
(4.41)
v@0D =
1
2
‰
-
1
2
t Ig+gDM
I‰t gD A2 H-g + gDL - A1 Hg + gDLM
t=0
=
1
2
HA2 H-g + gDL - A1 Hg + gDLL
Solving for A1 and A2
(4.42)
A1 =
-2 v0 + x0 H-g + gDL
2 gD
A2 =
2 v0 + x0 Hg + gDL
2 gD
and therefore the general solution becomes
(4.43)x@tD =
1
2 gD
‰
-
1
2
t Ig+gDM
I2 I-1 + ‰t gDM v0 + x0 I-g + gD + ‰t gD Hg + gDLMM
Note that this solution looks very much like our original solution for the underdamping case.
In particular if we let g2 - 4 w0
2 Ø Â 4 w0
2 - g2 = 2 Â wD, then the above solution becomes
(4.44)x@tD =
1
2 Â wD
‰
-
1
2
Ht gL
CoshB
2
2
t  wDF 2  wD x0 + SinhB
1
2
t 2 Â wDF H2 v0 + g x0L
Now, Cosh@Â yD =
‰Â y + ‰- y
2
= Cos@yD and Sinh@Â yD =
‰Â y - ‰- y
2
= Â Sin@yD so that the above
expression reduces to
4_DampedHarmonicOscillator.nb 11

11. x@tD = -
 ‰
-
t g
2 HÂ Sin@t wDD H2 v0 + g x0L + 2 Â Cos@t wDD x0 wDL
2 wD
= ‰
-
t g
2 Cos@t wDD x0 +
Sin@t wDD Jv0 +
g x0
2
N
wD
Equating x0 = Cos@fD and
v0 +
g
2
x0
wD
= Sin@fD, then the above solution becomes the solution for
an underdamped harmonic oscillator
(4.46)x@tD = Cos@f + t wDD x0
2
+
Jv0 +
g x0
2
N
2
wD
2
4.4 Quality Factor or Q
A dimensionless quantity used to measure the amount of damping is given by for a harmonic
oscillator is defined as
(4.47)Q = H2 pHaverage energy storedLL ê Henergy lost per cycleL
As defined the Q will be large if the damping is small. We know that the average energy is
given approximately by E@tD º E0 ‰-g tê2. The change is the energy in one period t is therefore
(4.48)DE = E@t0D - E@t + t0D = ‰-g t0 H1 - ‰-g t
L E0
For small damping g t << 1, one can expand the exponential, ‰-g t º 1 - g t + ... so that
(4.49)DE = ‰-g t0 g t E0
Substituting this into the expression for the Q
(4.50)Q =
2 ‰-g t0 p E0
‰-g t0 g t E0
=
2 p
g t
=
w
g
where we have used the fact that w =
2 p
t
. The following illustrates the behavior for several
values of the Q.
12 4_DampedHarmonicOscillator.nb

12. 4 6 8 10
= 0.0125664 Q = 500
0 2 4 6 8 10
-1.0
-0.5
0.0
0.5
1.0 g = 0.0314159 Q = 200
0 2 4 6
-1.0
-0.5
0.0
0.5
1.0 g = 0.0628319 Q =
4 6 8 10
g = 0.125664 Q = 50
0 2 4 6 8 10
-1.0
-0.5
0.0
0.5
1.0 g = 0.314159 Q = 20
0 2 4 6
-1.0
-0.5
0.0
0.5
1.0 g = 0.628319 Q =
4 6 8 10
g = 1.25664 Q = 5
0 2 4 6 8 10
-1.0
-0.5
0.0
0.5
1.0 g = 3.14159 Q = 2
0 2 4 6
-1.0
-0.5
0.0
0.5
1.0 g = 6.28319 Q =
4 6 8 10
g = 12.5664 Q = 0.5
0 2 4 6 8 10
-1.0
-0.5
0.0
0.5
1.0 g = 31.4159 Q = 0.2
0 2 4 6
-1.0
-0.5
0.0
0.5
1.0 g = 62.8319 Q =
4.5 Energy of Damped Harmonic Oscillator
Using the expression for an underdamped harmonic oscillator, x@tD = A Cos@wD t + fD e-g tê2, the
potential energy becomes
(4.51)PE =
1
2
k x@tD2
=
1
2
m w2
x@tD2
=
1
2
A2
‰-t g
m w2
Cos@f + t wDD2
To calculate the kinetic energy, first calculate the velocity
4_DampedHarmonicOscillator.nb 13

13. (4.52)v@tD = -
1
2
A ‰
-
t g
2 g Cos@f + t wDD - A ‰
-
t g
2 Sin@f + t wDD wD
and the kinetic energy becomes
(4.53)
PE =
1
2
m v@tD2
=
1
2
m -
1
2
A ‰
-
t g
2 g Cos@f + t wDD - A ‰
-
t g
2 Sin@f + t wDD wD
2
=
1
8
A2
‰-t g
k Hg Cos@f + t wDD + 2 Sin@f + t wDD wDL2
The total energy is then
(4.54)
E@tD =
1
8
A2
‰-t g
m
IIg2
+ 4 w2
M Cos@f + t wDD2
+ 2 g Sin@2 Hf + t wDLD wD + 4 Sin@f + t wDD2
wD
2
M
Substituting w2 =
g2
4
+ wD
2
(4.55)
E@tD =
1
4
A2
‰-t g
m Ig2
Cos@f + t wDD2
+ g Sin@2 Hf + t wDLD wD + 2 wD
2
M
E@tD =
1
2
A2
‰-t g
m wD
2
1 +
g2 Cos@f + t wDD2
2 wD
2
+
g Sin@2 Hf + t wDLD
2 wD
Plotting the total energies assuming f = 0.
14 4_DampedHarmonicOscillator.nb

14. tmax
g
w
0.0 0.2 0.4 0.6 0.8 1.0
0.0
0.2
0.4
0.6
0.8
1.0
1.2
............................................................
4_DampedHarmonicOscillator.nb 15