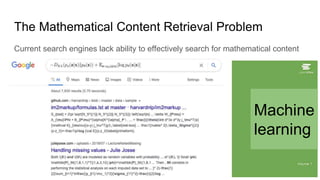
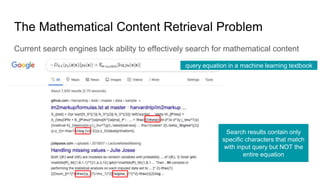
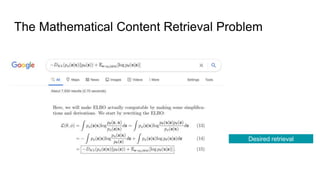
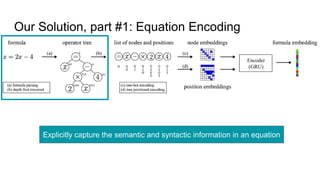
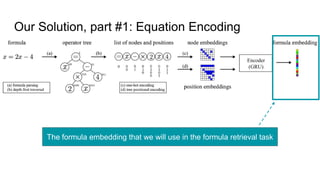
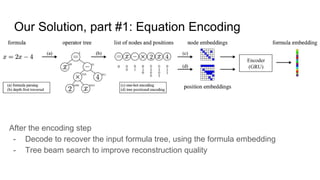
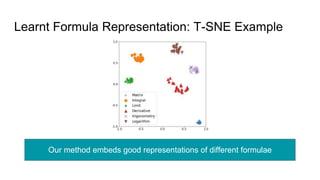
This document proposes a framework that uses tree embeddings to process mathematical language via encoding equations as trees. The framework includes a novel encoder-decoder architecture that learns representations of mathematical formulae. This approach achieves state-of-the-art performance on formula retrieval tasks by computing the similarity between embedding vectors of query and dataset equations. Future work will explore joint processing of math and text, deploying the system for textbook search, and using the embeddings for open-ended math problem solving.