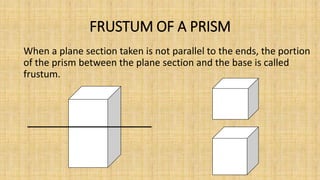
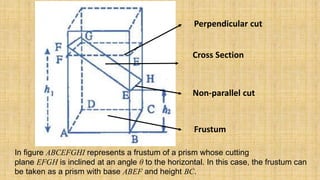
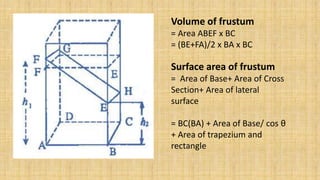
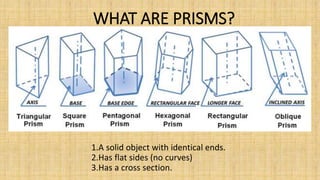
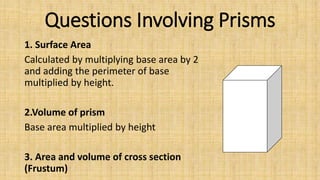
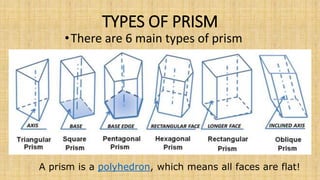
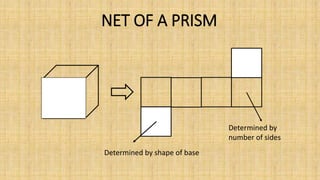
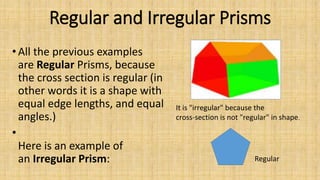
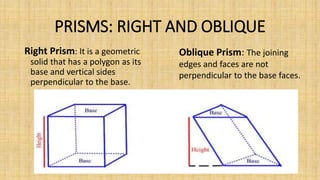
Prisms are solid geometric shapes that have two identical and parallel bases. There are six main types of prisms defined by the shape of their bases. Prisms can be regular if their cross-sections are regular polygons, or irregular if their cross-sections are irregular shapes. The surface area and volume of prisms can be calculated using formulas that involve the base area, perimeter or base, and height. A frustum is the portion of a prism cut by a plane that is not parallel to the bases, forming a new cross-sectional shape between the cut plane and one base.

1. PRISMS
and FRUSTUM
By: Alwin Ng, Ong Von Wan, Phares Phung, Chloe
The, Yip Xiao Jung, David Tan, Carol Tang, Alison

2. WHAT ARE PRISMS?
1.A solid object with identical ends.
2.Has flat sides (no curves)
3.Has a cross section.

3. Questions Involving Prisms
1. Surface Area
Calculated by multiplying base area by 2
and adding the perimeter of base
multiplied by height.
2.Volume of prism
Base area multiplied by height
3. Area and volume of cross section
(Frustum)

4. TYPES OF PRISM
•There are 6 main types of prism
A prism is a polyhedron, which means all faces are flat!

5. NET OF A PRISM
Determined by shape of base
Determined by
number of sides

6. Regular and Irregular Prisms
•All the previous examples
are Regular Prisms, because
the cross section is regular (in
other words it is a shape with
equal edge lengths, and equal
angles.)
•
Here is an example of
an Irregular Prism:
It is "irregular" because the
cross-section is not "regular" in shape.
Regular

7. PRISMS: RIGHT AND OBLIQUE
Right Prism: It is a geometric
solid that has a polygon as its
base and vertical sides
perpendicular to the base.
Oblique Prism: The joining
edges and faces are not
perpendicular to the base faces.

8. SURFACE AREA OF A PRISM
Area = 2b + ph
b = area of a base
p = perimeter of a base
h = height of the prism
Ex:
Surface Area
= 2(½ X 8 X 3) + [(8+5+5) X 12]
= 240 cm2

9. VOLUME OF A PRISM
Volume = bh
b = area of base
h = height
Example:
Volume = (½ X 8 X 3) X 12
= 144 cm3

10. FRUSTUM OF A PRISM
When a plane section taken is not parallel to the ends, the portion
of the prism between the plane section and the base is called
frustum.

11. Perpendicular cut
Non-parallel cut
Cross Section
Frustum
In figure ABCEFGHI represents a frustum of a prism whose cutting
plane EFGH is inclined at an angle θ to the horizontal. In this case, the frustum can
be taken as a prism with base ABEF and height BC.

12. Volume of frustum
= Area ABEF x BC
= (BE+FA)/2 x BA x BC
Surface area of frustum
= Area of Base+ Area of Cross
Section+ Area of lateral
surface
= BC(BA) + Area of Base/ cos θ
+ Area of trapezium and
rectangle