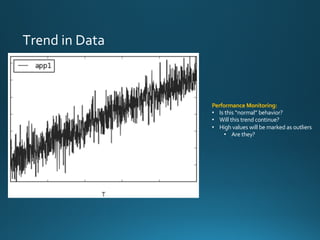
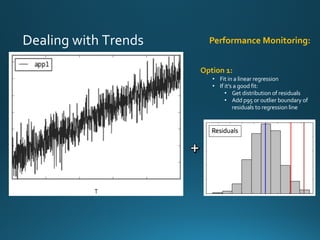
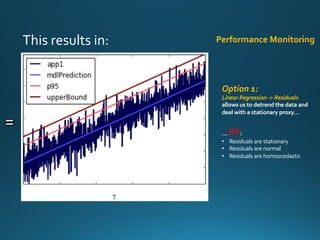
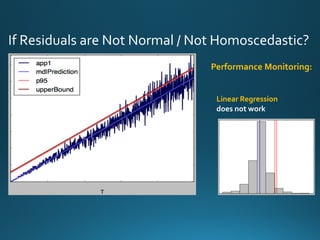
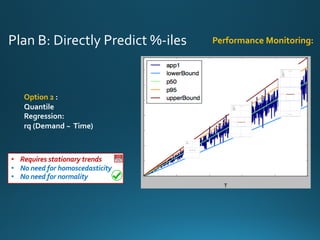
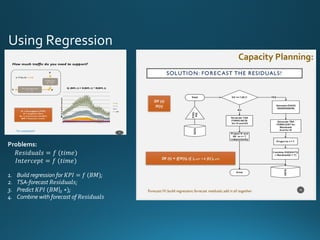
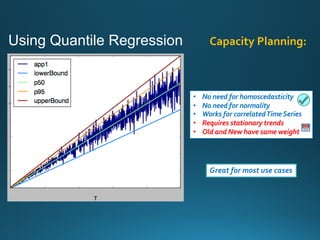
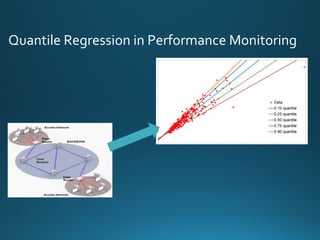
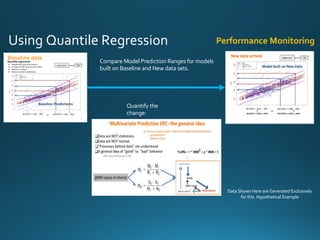
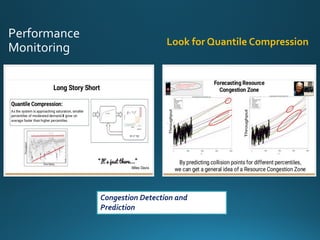
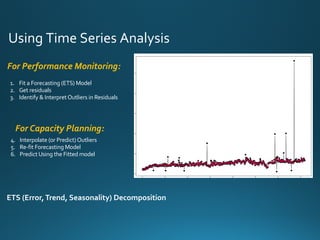
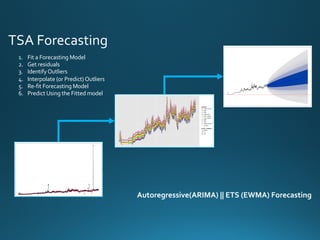
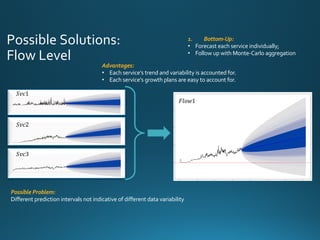
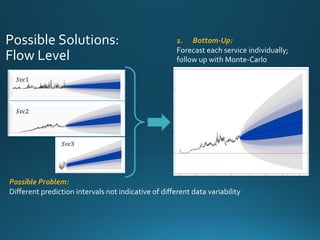
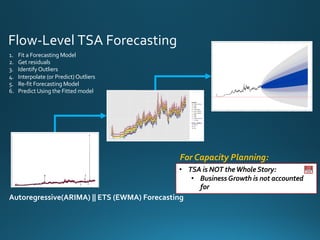
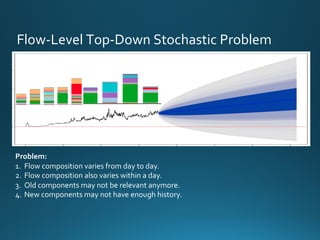
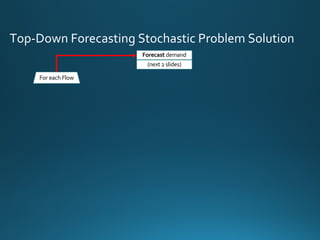
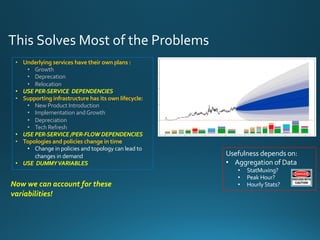
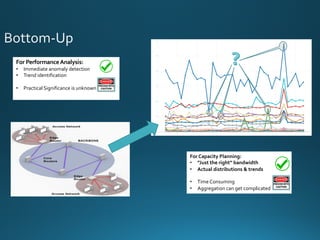
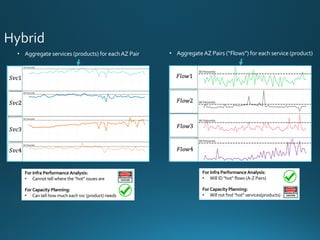
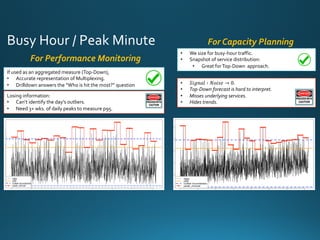
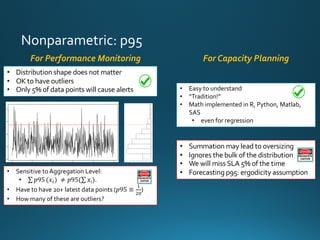
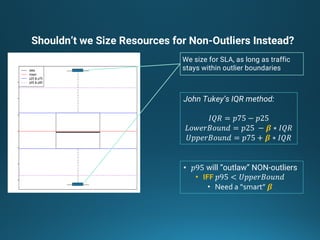
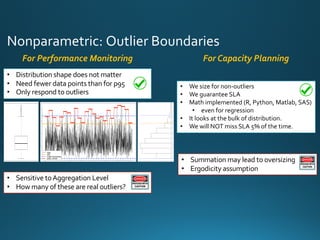
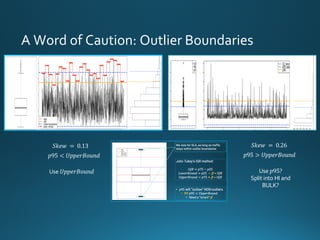
The document discusses various approaches and metrics for performance analysis and capacity planning in IT, highlighting the importance of understanding distinctions between performance and capacity metrics. It details methodologies for analyzing data trends, identifying outliers, and making forecasts to optimize resource allocation while addressing common challenges such as variability and changing demands. Additionally, it emphasizes the necessity of avoiding standardized metrics, advocating instead for tailored, data-driven strategies that account for the entirety of data distributions.

1. Different Approaches for DifferentTasks
CMG imPACt 2016
42nd International Conference by Computer Measurement Group
Alexander Gilgur, Steve Politis
Session 361
November 08, 2016
LaJolla, CA USA

2. Steve Politis
Josue Kuri
Alex Nikolaidis
Grace Smith
Yuri Smirnov
Tyler Price
Paul Sorenson
For contributing knowledge, ideas, solutions, and support

3. What’s the difference
between Performance
and Capacity?
• Two languages in the IT world
• Need tools, metrics, and stats
compatible with both languages
• Need fluency in both languages

4. • Metrics:
• Time (latency)
• Rate
• Count:
• Packets in flight
• Packet loss
• A few words about %
Utilization
• Models:
• Correlations
• Trends in Data
• Time-Series Analysis
• Approach
• Top-Down?
• Bottom-Up?
• Hybrid?
• Measures and Aggregations:
• 𝜇 + 𝑍 ∗ 𝜎
• Busy Hour/Peak Minute
• Nonparametric Measures:
• P95
• Outlier Boundaries

5. For Capacity Planning:
• Uncertainty: “Redistribution of wealth”
• Distribution Looks Gaussian
• Washout of local anomalies
For Performance Analysis:
• “Big Picture”
• Immediate impact assessment
• Drilldown is easier than aggregation:
• No need to worry about which
aggregation function to choose

6. For Performance Analysis:
• Immediate anomaly detection
• Trend identification
• Practical Significance is unknown
For Capacity Planning:
• ”Just the right” bandwidth
• Actual distributions & trends
• Time Consuming
• Aggregation can get complicated

7. • Aggregate AZ Pairs (“Flows”) for each service (product)• Aggregate services (products) for each AZ Pair
For Infra Performance Analysis:
• Cannot tell where the “hot” issues are
For Capacity Planning:
• Can tell how much each svc (product) needs
For Infra Performance Analysis:
• Will ID “hot” flows (A-Z Pairs)
For Capacity Planning:
• Will not find “hot” services(products)

8. • Metrics:
• Time (latency)
• Rate
• Count:
• Packets in flight
• Packet loss
• A few words about %
Utilization
• Models:
• Correlations
• Trends in Data
• Time-Series Analysis
• Approach
• Top-Down?
• Bottom-Up?
• Hybrid?
• Measures and Aggregations:
• 𝜇 + 𝑍 ∗ 𝜎
• Busy Hour/Peak Minute
• Nonparametric Measures:
• P95
• Outlier Boundaries

9. [𝜇 − 𝑍 ∗ 𝜎, 𝜇 + 𝑍 ∗ 𝜎]
• The 𝑍 is arbitrary
• Assumptions about the distribution:
• Mean andVariance defined
• Gaussian (Symmetrical)
• Stationary
• No outliers
• Simple math:
• Addition
• Regression
• TSA Forecasting

10. [𝜇 − 𝑍 ∗ 𝜎, 𝜇 + 𝑍 ∗ 𝜎] [𝜇 − 𝑍 𝟏 ∗ 𝜎, 𝜇 + 𝑍 𝟐 ∗ 𝜎]
𝑆𝑎𝑚𝑝𝑙𝑖𝑛𝑔:
With enough random samples, their
means will be Gaussian
(Central LimitTheorem)
𝐷𝑎𝑡𝑎 𝑇𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛:
• log
• exp
• Box-CoxFor Capacity Planning: For Monitoring:

11. Busy Hour / Peak Minute
Losing information:
• Can’t identify the day’s outliers.
• Need 3+ wks. of daily peaks to measure p95.
For Performance Monitoring
For Capacity Planning
• 𝑆𝑖𝑔𝑛𝑎𝑙 ∶ 𝑁𝑜𝑖𝑠𝑒 → 0.
• Top-Down forecast is hard to interpret.
• Misses underlying services.
• Hides trends.
If used as an aggregated measure (Top-Down),
• Accurate representation of Multiplexing.
• Drilldown answers the “Who is hit the most?” question
• We size for busy-hour traffic.
• Snapshot of service distribution:
• Great forTop-Down approach.

12. Nonparametric: p95
• Sensitive to Aggregation Level:
• ∑ 𝑝95 (𝑥G) ≠ 𝑝95(∑ 𝑥𝑖).
• Have to have 20+ latest data points (𝑝95 ≡
K
LM
)
• How many of these are outliers?
For Performance Monitoring For Capacity Planning
• Summation may lead to oversizing
• Ignores the bulk of the distribution
• We will miss SLA 5% of the time
• Forecasting p95: ergodicity assumption
• Distribution shape does not matter
• OK to have outliers
• Only 5% of data points will cause alerts • Easy to understand
• “Tradition!”
• Math implemented in R, Python, Matlab, SAS
• even for regression

13. Should we Size Hardware for 𝒑𝟗𝟓 ?
5% of the time
SLO (99.9%? 99.999%?)
will be violated

14. Shouldn’t we Size Resources for Non-Outliers Instead?
We size for SLA, as long as traffic
stays within outlier boundaries
John Tukey’s IQR method:
𝐼𝑄𝑅 = 𝑝75 − 𝑝25
𝐿𝑜𝑤𝑒𝑟𝐵𝑜𝑢𝑛𝑑 = 𝑝25 − 𝜷 ∗ 𝐼𝑄𝑅
𝑈𝑝𝑝𝑒𝑟𝐵𝑜𝑢𝑛𝑑 = 𝑝75 + 𝜷 ∗ 𝐼𝑄𝑅
• 𝑝95 will “outlaw” NON-outliers
• IFF 𝑝95 < 𝑈𝑝𝑝𝑒𝑟𝐵𝑜𝑢𝑛𝑑
• Need a “smart” 𝜷

15. Nonparametric: Outlier Boundaries
• Sensitive to Aggregation Level
• How many of these are real outliers?
For Performance Monitoring For Capacity Planning
• Summation may lead to oversizing
• Ergodicity assumption
• We size for non-outliers
• We guarantee SLA
• Math implemented (R, Python, Matlab, SAS)
• even for regression
• It looks at the bulk of distribution.
• We will NOT miss SLA 5% of the time.
• Distribution shape does not matter
• Need fewer data points than for p95
• Only respond to outliers

16. A Word of Caution: Outlier Boundaries
𝑆𝑘𝑒𝑤 = 0.13 𝑆𝑘𝑒𝑤 = 0.26
𝑝95 < 𝑈𝑝𝑝𝑒𝑟𝐵𝑜𝑢𝑛𝑑 𝑝95 > 𝑈𝑝𝑝𝑒𝑟𝐵𝑜𝑢𝑛𝑑
Use 𝑈𝑝𝑝𝑒𝑟𝐵𝑜𝑢𝑛𝑑 Use 𝑝95?
Split into HI and BULK?

17. • There is no “one size fits all” approach.
• There is no “one size fits all” statistic.
• There are common principles:
• Aggregate before computing percentiles.
• Use Outlier Boundaries:
• Performance & Capacity:
• Accounts for the bulk of the data;
• Distribution does not matter;
• Performance:
• Easy to ID outliers;
• Capacity:
• Sizing for Non-Outliers => less $
• Avoid Predefined Percentiles.
• Metrics:
• Time (latency)
• Rate
• Count:
• Packets in flight; Packet Loss; % Utilization
• Models:
• Correlations
• Trends in Data
Coming Next

18. User Metrics:
• throughput
• latency
• data loss
• data loss & latency
• latency & data loss
TheWhirlpool of Metrics
For Monitoring
Real metrics:
• # of Packets in Flight
• # of Packets in Queue or Lost
For Capacity Planning
Traditional Metrics in Planning:
• 𝑇ℎ𝑟𝑜𝑢𝑔ℎ𝑝𝑢𝑡 [Gbps]
• 𝐿𝑎𝑡𝑒𝑛𝑐𝑦hijklm
• 𝐿𝑎𝑡𝑒𝑛𝑐𝑦hinl = 𝑙𝑜𝑎𝑑𝑖𝑛𝑔 || 𝑟𝑒𝑎𝑠𝑠𝑒𝑚𝑏𝑙𝑦
• Packets get queued and blocked.
• Bits may be bursty while packets are smooth.
• Reverse statement is true as well.
• 𝐿𝑎𝑡𝑒𝑛𝑐𝑦hijklm = 𝑡𝑟𝑎𝑛𝑠𝑝𝑜𝑟𝑡 + 𝑞𝑢𝑒𝑢𝑒𝑖𝑛𝑔
• Packets need capacity.
• Packet sizes vary => capacity [Gbps]
Example:
320 𝐺𝑏𝑝𝑠 = 26.7𝑀 ∗
1.5𝑘𝐵 ∗ 8 𝑏𝑖𝑡𝑠
𝑠𝑒𝑐
320 𝐺𝑏𝑝𝑠 = 10 ∗
4𝐺𝑖𝐵 ∗ 8 𝑏𝑖𝑡𝑠
𝑠𝑒𝑐
Traditional Metrics for Monitoring:
• % Utilization
• Packet Loss Rate

19. Time, Rate, Count, and Utilization
𝑃 𝑞 = 𝐸𝑟𝑙𝑎𝑛𝑔𝐶 (𝑁, 𝐶)
Packet Queueing:
𝑃 𝑏 = 𝐸𝑟𝑙𝑎𝑛𝑔𝐵 (𝑁, 𝐶)
Packet Blocking:
2012 paper
𝑁 = 𝑃𝑃𝑆 ∗ 𝐿𝑎𝑡𝑒𝑛𝑐𝑦
𝐿𝑎𝑡𝑒𝑛𝑐𝑦 =
1
2
∗ 𝑅𝑇𝑇 + 𝑇€•‚‚
𝑏𝑝𝑠 = 𝑃𝑃𝑆 ∗
𝑏𝑖𝑡𝑠
𝑝𝑎𝑐𝑘𝑒𝑡
𝐶 = 𝑚𝑎 𝑥 𝑃𝑃𝑆 ∗
1
2
∗ 𝑅𝑇𝑇
2006 paper
(CPU centric)
• Utilization CAN BE useless
• If the metric does not
reflect what it is used for.
links were utilized
near 100% [
€hƒ
€hƒ
] but
no packet drops

20. • There is no “one size fits all” approach.
• There is no “one size fits all” statistic.
• There are common principles:
• Aggregate before computing percentiles.
• Use a statistic that accounts for the bulk of the data.
• Metric = what’s important to the BW user:
• Quality of Service (QoS):
• Network Latency
• Packets lost
• Models:
• Trend in Data
• Correlation
• Time-Series Analysis
Coming Next

21. Trend in Data
Performance Monitoring:
• Is this “normal” behavior?
• Will this trend continue?
• High values will be marked as outliers
• Are they?

22. Dealing with Trends
Option 1:
• Fit in a linear regression
• If it’s a good fit:
• Get distribution of residuals
• Add p95 or outlier boundary of
residuals to regression line
Performance Monitoring:

23. This results in:
Option 1:
Linear Regression -> Residuals
allows us to detrend the data and
deal with a stationary proxy…
… IFF:
• Residuals are stationary
• Residuals are normal
• Residuals are homoscedastic
Performance Monitoring

24. If Residuals are Not Normal / Not Homoscedastic?
Linear Regression
does not work
Performance Monitoring:

25. Plan B: Directly Predict %-iles
Option 2 :
Quantile Regression:
rq (Demand ~ Time)
Performance Monitoring:
• Requires stationary trends
• No need for homoscedasticity
• No need for normality

26. Using Regression
1. Build regression for 𝐾𝑃𝐼 = 𝑓 (𝐵𝑀);
2. TSA-forecast 𝑅𝑒𝑠𝑖𝑑𝑢𝑎𝑙𝑠;
3. Predict 𝐾𝑃𝐼 (𝐵𝑀|m ∗);
4. Combine with forecast of 𝑅𝑒𝑠𝑖𝑑𝑢𝑎𝑙𝑠
Capacity Planning:
Problems:
𝑅𝑒𝑠𝑖𝑑𝑢𝑎𝑙𝑠 = 𝑓 (𝑡𝑖𝑚𝑒)
𝐼𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡 = 𝑓 (𝑡𝑖𝑚𝑒)

27. Using Quantile Regression Capacity Planning:
Great for most use cases
• No need for homoscedasticity
• No need for normality
• Works for correlatedTime Series
• Requires stationary trends
• Old and New have same weight

28. Quantile Regression in Performance Monitoring

29. Using Quantile Regression Performance Monitoring
Compare Model Prediction Ranges for models
built on Baseline and New data sets.
Quantify the change:
Baseline data
Data Shown Here are Generated Exclusively
for this Hypothetical Example

30. Performance Monitoring Look for Quantile Compression
Congestion Detection and Prediction

31. Time Series Analysis

32. Using Time Series Analysis
ETS (Error,Trend, Seasonality) Decomposition
For Performance Monitoring:
1. Fit a Forecasting (ETS) Model
2. Get residuals
3. Identify & Interpret Outliers in Residuals
4. Interpolate (or Predict) Outliers
5. Re-fit Forecasting Model
6. Predict Using the Fitted model
For Capacity Planning:

33. TSA Forecasting
Autoregressive(ARIMA) || ETS (EWMA) Forecasting
1. Fit a Forecasting Model
2. Get residuals
3. Identify Outliers
4. Interpolate (or Predict) Outliers
5. Re-fit Forecasting Model
6. Predict Using the Fitted model

34. Issues / Problems / Challenges
How can we account for these variabilities?
• Underlying services have their own plans:
• Growth
• Deprecation
• Relocation
• Supporting infrastructure has its own lifecycle:
• New Product Introduction
• Implementation and Growth
• Depreciation
• Tech Refresh
• Topologies and policies change in time
• Change in policies and topology can lead to
changes in demand

35. Possible Solutions:
Flow Level
1. Bottom-Up:
• Forecast each service individually;
• Follow up with Monte-Carlo aggregation
𝑆𝑣𝑐1
𝑆𝑣𝑐2
𝑆𝑣𝑐3
Possible Problem:
Different prediction intervals not indicative of different data variability
Advantages:
• Each service’s trend and variability is accounted for.
• Each service’s growth plans are easy to account for.
𝐹𝑙𝑜𝑤1

36. 1. Bottom-Up:
Forecast each service individually;
follow up with Monte-Carlo aggregation
Possible Problem:
Different prediction intervals not indicative of different data variability
Possible Solutions:
Flow Level
𝑆𝑣𝑐1
𝑆𝑣𝑐2
𝑆𝑣𝑐3

37. 2.Top-Down:
• Forecast the flow.
• Get Distribution of each component’s weight in the flow.
• Compute each component’s demand forecast
Possible Problems:
ComponentWeights can drift in time
Interaction and Contention => “unknown unknown”
Possible Solutions:
Flow Level
Solutions:
Estimate ComponentWeights
Account for Quantile Compression
𝑆𝑣𝑐1
𝑆𝑣𝑐2
𝑆𝑣𝑐3
𝑆𝑣𝑐3 𝑆𝑣𝑐2
𝑆𝑣𝑐1

38. Flow-Level TSA Forecasting
Autoregressive(ARIMA) || ETS (EWMA) Forecasting
1. Fit a Forecasting Model
2. Get residuals
3. Identify Outliers
4. Interpolate (or Predict) Outliers
5. Re-fit Forecasting Model
6. Predict Using the Fitted model
For Capacity Planning:
• TSA is NOT theWhole Story:
• Business Growth is not accounted for

39. Flow-Level Top-Down Stochastic Problem
Problem:
1. Flow composition varies from day to day.
2. Flow composition also varies within a day.
3. Old components may not be relevant anymore.
4. New components may not have enough history.

40. Top-Down Forecasting Stochastic Problem Solution
For each Flow
Forecast demand
(next 2 slides)

41. Stochastic Problem Solution
For each Flow
For each
Service
Identify Services
active in this Flow
Compute Stats:
lower_bound
min
p05
p10
p25
p50
Mean
StDev
p75
p90
p95
p99
max
upper_bound
For each
Hour
Forecast demand

42. For each Flow
For each
Service
Identify Services
active in this Flow
Compute Stats:
lower_bound
min
p05
p10
p25
p50
Mean
StDev
p75
p90
p95
p99
max
upper_bound
For each
Hour
Compute this Svc’s
weight for this Stat
For each Stat
(long-term means)
Infer unconstrained
weights
(use long-term skew)
Forecast demand
Top-Down Forecasting Stochastic Problem Solution

43. For each Flow
For each
Service
Identify Services
active in this Flow
Compute Stats:
lower_bound
min
p05
p10
p25
p50
Mean
StDev
p75
p90
p95
p99
max
upper_bound
For each
Hour
Compute this Svc’s
weight for this Stat
For each Stat
(long-term means)
Infer unconstrained
weights
(use long-term skew)
Forecast demand
𝐹𝑐𝑠𝑡‚ˆ‰Š ∗ 𝑊𝑒𝑖𝑔ℎ𝑡ƒŒj
Solution to Top-Down Forecasting Stochastic Problem

44. This Solves Most of the Problems
• Underlying services have their own plans :
• Growth
• Deprecation
• Relocation
• USE PER-SERVICE DEPENDENCIES
• Supporting infrastructure has its own lifecycle:
• New Product Introduction
• Implementation and Growth
• Depreciation
• Tech Refresh
• USE PER-SERVICE /PER-FLOW DEPENDENCIES
• Topologies and policies change in time
• Change in policies and topology can lead to
changes in demand
• USE DUMMY VARIABLES
Now we can account for these variabilities!
Usefulness depends on:
• Aggregation of Data
• StatMuxing?
• Peak Hour?
• Hourly Stats?

45. • Forecast Demand based on the Model
• Bottoms-Up
• 𝑇𝑟𝑎𝑓𝑓𝑖𝑐 ∗ 𝑄𝑜𝑆 Drives 𝐷𝐶 𝐿𝑜𝑎𝑑 Drives 𝑆𝑝𝑎𝑐𝑒 & 𝑃𝑜𝑤𝑒𝑟
• Account for QoS in Demand Forecasting
• Plan for SLO
• DO NOT Assume Anything!
• Especially about Shapes of Distributions.
• Mean andVariance are Overrated!
• So is 𝑝95!
• Use Outlier Boundaries (“fences”)
• Size Systems for “would-be-unbounded” forecasts
• DO Use Entire Distribution to be Proactive

46. agilgur@fb.com / alexgilgur@gmail.com
spolitis@fb.com

47. All data in this presentation are generated solely for illustration purposes
Select images and formulae are provided with permission from Facebook

49. Capacity Planning
Is the number of Gbps on a constrained system indicative of demand?
Is it right to forecast upper bound of traffic on a constrained system?
• Use 𝑝25, 𝑝50, and 𝑝75 to compute the 𝑆𝑘𝑒𝑤
• Forecast 𝑝25 and 𝑝50
• Use the 𝑆𝑘𝑒𝑤 to infer forecast of 𝑝75•Žj‰Žƒm•iGŽl•
• Compute the forecast of 𝑈𝑝𝑝𝑒𝑟𝐵𝑜𝑢𝑛𝑑
Resource Constraint =>
Quantile Compression =>
Underforecasting the load =>
Undersizing the resource
Account for Quantile Compression

50. What is Quantile Compression?