metodo castigliano

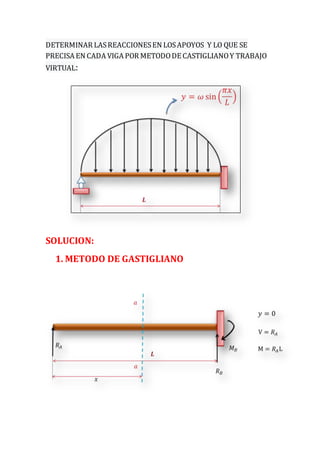
1. DETERMINAR LASREACCIONESEN LOSAPOYOS Y LO QUE SE
PRECISA EN CADA VIGA POR METODODE CASTIGLIANOY TRABAJO
VIRTUAL:
SOLUCION:
1. METODO DE GASTIGLIANO

2. 𝑦 = 𝑤𝑠𝑒𝑛 (
𝜋𝑥
𝑙
)
𝑉 = ∫ 𝑦 = ∫ 𝑤𝑠𝑒𝑛 (
𝜋𝑥
𝑙
)
𝑥
0
𝑑𝑥 =
−𝑤𝑙
𝜋
[cos(
𝜋𝑥
𝑙
) − 1]
𝑀 = ∫ 𝑉𝑑𝑥 = ∫
−𝑤𝐿
𝜋
[cos(
𝜋𝑥
𝐿
) − 1]
𝑥
0
𝑑𝑥 =
−𝑤𝑙2
𝜋2
[sen(
𝜋𝑥
𝐿
)] +
𝑤𝐿𝑥
𝜋
a) ECUACIÓN
𝑀 𝑎 = 𝑅 𝐴 𝑥 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)……(1)
b) DERIVADA PARCIAL
𝜕𝑀 𝑎
𝜕𝑅 𝐴
= 𝑥
c) SEGUNDO TEOREMA DE CASTIGLIANO:
𝛿 = ∫ 𝑀 𝑎 (
𝜕𝑀 𝑎
𝜕𝑅 𝐴
) = 0
𝐿
0

3. 𝛿 = ∫ ( 𝑅 𝐴 𝑥 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)) ( 𝑥) 𝑑𝑥 = 0
𝐿
0
𝛿 = ∫ ( 𝑅 𝐴 𝑥2
−
𝜔𝐿
𝜋
𝑥2
+
𝜔𝐿2
𝑥
𝜋2
𝑠𝑖𝑛(
𝜋𝑥
𝐿
)) 𝑑𝑥 = 0
𝐿
0
[𝑅 𝐴
𝑥3
3
−
𝜔𝐿
𝜋
𝑥3
3
−
𝜔𝐿3 𝑥
𝜋3
𝑐𝑜𝑠 (
𝜋𝑥
𝐿
) +
𝜔𝐿4
𝜋4
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)]
𝐿
0
= 0
𝑅 𝐴
𝐿3
3
−
𝜔𝐿4
3𝜋
+
𝜔𝐿4
𝜋3
= 0
𝑅 𝐴 =
𝜔𝐿
𝜋
−
3𝜔𝐿
𝜋3
 POR ESTATICA:
 ∑ 𝐹𝑣 = 0
𝑅 𝐴 + 𝑅 𝐵 =
2𝜔𝐿
𝜋
𝑅 𝐵 =
2𝜔𝐿
𝜋
+
3𝜔𝐿
𝜋3
−
𝜔𝐿
𝜋

4. 𝑅 𝐵 =
𝜔𝐿
𝜋
+
3𝜔𝐿
𝜋3
 ∑ 𝑀𝐴 = 0
𝑅 𝐵 𝐿 − 𝑀 𝐵 −
2𝜔𝐿
𝜋
𝐿
2
= 0
𝑀 𝐵 = (
𝜔𝐿
𝜋
+
3𝜔𝐿
𝜋3
) 𝐿 −
𝜔𝐿2
𝜋
𝑀 𝐵 =
𝜔𝐿2
𝜋
+
3𝜔𝐿2
𝜋3
−
𝜔𝐿2
𝜋
𝑀 𝐵 =
3𝜔𝐿2
𝜋3
 DETERMINAMOSELGIROEN EL APOYOSIMPLE:
𝑀 𝑎 = 𝑅 𝐴 𝑥 − 𝑚 𝑎 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛(
𝜋𝑥
𝐿
)
 DERIVADA PARCIAL

5. 𝜕𝑀 𝑎
𝜕𝑚 𝑎
= −1
 PRIMER TEOREMA DE CASTIGLIANO:
𝜃 =
1
𝐸𝐼
∫ 𝑀 𝑎 (
𝜕𝑀 𝑎
𝜕𝑚 𝑎
)
𝐿
0
𝜃 =
1
𝐸𝐼
∫ (𝑅 𝐴 𝑥 − 𝑚 𝑎 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛(
𝜋𝑥
𝐿
))(−1)
𝐿
0
𝑑𝑥
𝜃 =
1
𝐸𝐼
∫ (−𝑅 𝐴 𝑥 +
𝜔𝐿
𝜋
𝑥 −
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
))
𝐿
0
𝑑𝑥
REEMPLZANDO 𝑅 𝐴 EN ESTA ÚLTIMA ECUACION
𝜃 =
1
𝐸𝐼
∫ (−(
𝜔𝐿
𝜋
−
3𝜔𝐿
𝜋3
) 𝑥 +
𝜔𝐿
𝜋
𝑥 −
𝜔𝐿2
𝜋2
𝑠𝑖𝑛(
𝜋𝑥
𝐿
))
𝐿
0
𝑑𝑥
INTEGRANDOY EVALUANDOTENEMOS:
𝜃 = −
𝜔𝐿3
2𝜋3
EL SIFNO NEGATIVOINDICA QUE LA FUERZA APLICADA (MOMENTO
𝑚 𝑎 ) DEBE ESTAR EN SENTIDO HORARIO
𝜃 =
𝜔𝐿3
2𝜋3
2. POR TRABAJO VIRTUAL:
DETERMINAMOSLA DEFLEXION EN EL APOYOSIMPLE:

6. DETERMINAMOS LA ECUACION DEL MOMENTO REAL:
𝑀 𝑎 = 𝑅 𝐴 𝑥 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)
EL MOMENTO VIRTUAL SERA:
𝑚 𝑣𝑎 = 𝑚 𝑎 = 1
LA ECUACION DE TRABAJO VIRTUAL PARA LA DEFLEXION
EN EL APOYO SIMPLE:
𝜃 =
1
𝐸𝐼
∫ 𝑀 𝑎 ∗ 𝑚 𝑣𝑎 𝑑𝑥
𝐿
0
𝜃 =
1
𝐸𝐼
∫ ( 𝑅 𝐴 𝑥 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)) (1) 𝑑𝑥
𝐿
0
REEMPLZANDO 𝑅 𝐴 EN ESTA ÚLTIMA ECUACION

7. 𝜃 =
1
𝐸𝐼
∫ ((
𝜔𝐿
𝜋
−
3𝜔𝐿
𝜋3
)𝑥 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
))
𝐿
0
𝑑𝑥
INTEGRANDOY EVALUANDOTENEMOS:
𝜃 =
𝜔𝐿3
2𝜋3

8. 3. DETERMINAR LAS REACCIONES EN LOS APOYOS Y LO QUE SE
PRECISA EN CADA VIGA POR METODO DE CASTIGLIANO Y
TRABAJO VIRTUAL:
SOLUCION:
4. METODO DE GASTIGLIANO
a) ISOSTATIZANDO

9. 𝑦 = 𝑤𝑠𝑒𝑛 (
𝜋𝑥
𝑙
)
𝑉 = ∫ 𝑦 = ∫ 𝑤𝑠𝑒𝑛 (
𝜋𝑥
𝑙
)
𝑥
0
𝑑𝑥 =
−𝑤𝑙
𝜋
[cos(
𝜋𝑥
𝑙
) − 1]
𝑀 = ∫ 𝑉𝑑𝑥 = ∫
−𝑤𝐿
𝜋
[cos(
𝜋𝑥
𝐿
) − 1]
𝑥
0
𝑑𝑥 =
−𝑤𝑙2
𝜋2
[sen(
𝜋𝑥
𝐿
)] +
𝑤𝐿𝑥
𝜋
d) ECUACIÓN
𝑀 𝑎 = 𝑅 𝐴 𝑥 − 𝑀𝐴 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)……(1)
e) DERIVADA PARCIAL

10. 𝜕𝑀 𝑎
𝜕𝑀𝐴
= −1 𝑦
𝜕𝑀 𝑎
𝜕𝑅 𝐴
= 𝑥 … … (2)
f) SEGUNDO TEOREMA DE CASTIGLIANO:
𝜃 = ∫ 𝑀 𝑎 (
𝜕 𝑀 𝑎
𝜕𝑀 𝐴
) = 0
𝐿
0
- REEPLAZANDO(1) Y (2):
𝜃𝐴 = ∫ ( 𝑅 𝐴 𝑥 − 𝑀 𝐴 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛(
𝜋𝑥
𝐿
)) (−1) = 0
𝐿
0
[−𝑅 𝐴
𝑥2
2
+ 𝑀 𝐴 𝑥 +
𝜔𝐿
𝜋
𝑥2
2
+
𝜔𝐿3
𝜋3
𝑐𝑜𝑠 (
𝜋𝑥
𝐿
)]
𝐿
0
= 0
[−𝑅 𝐴
𝐿2
2
+ 𝑀 𝐴 𝐿 +
𝜔𝐿
𝜋
𝐿2
2
+
𝜔𝐿3
𝜋3
𝑐𝑜𝑠 (
𝜋𝐿
𝐿
) −
𝜔𝐿3
𝜋3
] = 0
[−
𝑅 𝐴 𝐿
2
+ 𝑀 𝐴 +
𝜔𝐿2
2𝜋
−
2𝜔𝐿2
𝜋3
] = 0 … … (3)
𝛿 = ∫ 𝑀 𝑎 (
𝜕𝑀 𝑎
𝜕𝑅 𝐴
) = 0
𝐿
0
𝛿𝐴 = ∫ ( 𝑅 𝐴 𝑥 − 𝑀 𝐴 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)) ( 𝑥) = 0
𝐿
0
𝛿𝐴 = ∫ ( 𝑅 𝐴 𝑥2
− 𝑀 𝐴 𝑥 −
𝜔𝐿
𝜋
𝑥2
+
𝜔𝐿2
𝑥
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)) = 0
𝐿
0
[𝑅 𝐴
𝑥3
3
− 𝑀𝐴
𝑥2
2
−
𝜔𝐿
𝜋
𝑥3
3
−
𝜔𝐿3
𝑥
𝜋3
𝑐𝑜𝑠 (
𝜋𝑥
𝐿
) +
𝜔𝐿4
𝜋4
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)]
𝐿
0
= 0

11. [𝑅 𝐴
𝐿3
3
− 𝑀𝐴
𝐿2
2
−
𝜔𝐿
𝜋
𝐿3
3
− (−
𝜔𝐿3
𝐿
𝜋3
)] = 0
𝑅 𝐴
𝐿
3
−
𝑀𝐴
2
−
𝜔𝐿2
3𝜋
+
𝜔𝐿2
𝜋3
= 0… …(4)
- Multiplicando la ecuación(4) por 2, sumando con la
ecuación(3), tenemos:
2𝑅 𝐴
𝐿
3
−
2𝜔𝐿2
3𝜋
+
2𝜔𝐿2
𝜋3
−
𝑅 𝐴 𝐿
2
+
𝜔𝐿2
2𝜋
−
2𝜔𝐿2
𝜋3
= 0
𝑅 𝐴 𝐿
6
−
𝜔𝐿2
6𝜋
= 0
𝑅 𝐴 =
𝜔𝐿
𝜋
- Reemplazando 𝑅 𝐴 en la ecuación (3), tenemos:
[−
𝜔𝐿
𝜋
𝐿
2
+ 𝑀 𝐴 +
𝜔𝐿2
2𝜋
−
2𝜔𝐿2
𝜋3
] = 0
𝑀𝐴 =
2𝜔𝐿2
𝜋3
 POR SIMETRIA:
𝑅 𝐴= 𝑅 𝐵 =
𝜔𝐿
𝜋
𝑀𝐴 = 𝑀 𝐵 =
2𝜔𝐿2
𝜋3

12.  LA DEFLEXION EN EL CENTRO DE LA LUZ SERA:
𝑀 𝑎 = 𝑅 𝐴 𝑥 − 𝑀𝐴 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛(
𝜋𝑥
𝐿
) − 𝑃(𝑥 −
𝐿
2
)
𝜕𝑀 𝑎
𝜕𝑃
= − ( 𝑥 −
𝐿
2
)
 POR EL PRIMER TEOREMA DE CASTIGLIANO:
𝛿 =
1
𝐸𝐼
∫ 𝑀 𝑎 (
𝜕𝑀 𝑎
𝜕𝑃
)
𝐿
0
𝛿 =
1
𝐸𝐼
∫ ( 𝑅 𝐴 𝑥 − 𝑀 𝐴 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
) − 𝑃(𝑥 −
𝐿
2
))(
𝐿
2
− 𝑥) 𝑑𝑥
𝐿
𝐿
2
𝛿 =
1
𝐸𝐼
∫ ( 𝑅 𝐴 (
𝐿𝑥
2
− 𝑥2
) − 𝑀 𝐴 (
𝐿
2
− 𝑥) −
𝜔𝐿
𝜋
(
𝐿𝑥
2
− 𝑥2
)
𝐿
𝐿
2
+
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)(
𝐿
2
− 𝑥)) 𝑑𝑥
 INTEGRANDO Y EVALUANDO:
𝛿 = −
𝜔𝜋𝐿4
− 4𝜔𝐿4
4𝜋4

13. 𝛿 =
𝜔𝐿4
𝜋4
−
𝜔𝐿4
4𝜋3
𝛿 =
𝜔𝐿4
𝜋3
(
1
𝜋
−
1
4
)
 POR TRABAJO VIRTUAL
APLICAMOS UNA FUERZA UNITARIA EN EL CENTRO DE
LA VIGA PARA DETERMINAR LA DEFLEXION EN EL
CENTRO DE LA LUZ:
DETERMIANOS LA ECUACION DEL MOENTO REAL:
𝑀 𝑎 = 𝑅 𝐴 𝑥 − 𝑀𝐴 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
)
LA ECUACION DE MOMENTO VIRTUAL:
𝑚 𝑎 = −1(𝑥 −
𝐿
2
)

14. PLANTEAMOS LA ECUACION DE TRABAJO VIRTUAL
PARA DETERMINAR LA DEFLEXION EN EL CENTRO DE
LA LUZ:
𝛿 =
1
𝐸𝐼
∫ 𝑀 𝑎 ∗ 𝑚 𝑣𝑎 𝑑𝑥
𝐿
0
𝛿 =
1
𝐸𝐼
∫ ( 𝑅 𝐴 𝑥 − 𝑀 𝐴 −
𝜔𝐿
𝜋
𝑥 +
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
))(−1 ( 𝑥 −
𝐿
2
)) 𝑑𝑥
𝐿
0
𝛿 =
1
𝐸𝐼
∫ ( 𝑅 𝐴 (
𝐿𝑥
2
− 𝑥2
) − 𝑀 𝐴 (
𝐿
2
− 𝑥) −
𝜔𝐿
𝜋
(
𝐿𝑥
2
− 𝑥2
)
𝐿
𝐿
2
+
𝜔𝐿2
𝜋2
𝑠𝑖𝑛 (
𝜋𝑥
𝐿
) (
𝐿
2
− 𝑥)) 𝑑𝑥
 INTEGRANDO Y EVALUANDO:
𝛿 = −
𝜔𝜋𝐿4
− 4𝜔𝐿4
4𝜋4
𝛿 =
𝜔𝐿4
𝜋4
−
𝜔𝐿4
4𝜋3
𝛿 =
𝜔𝐿4
𝜋3
(
1
𝜋
−
1
4
)
SEGUNDA PARTE:
DIBUJAR LOS DIAGRAMASDE N,V Y M
DETERMINAR ELDESPLAZAMIENTOEN ELAPOYOLIBRE 𝑢2, 𝑣2 y
𝜃2

15. SOLUCION:
ES HIPERESTATICA, SELECCIONAMOSUNA FUERZA REDUDANTE, EN
ESTE CASO H1
PRIMER PASO: LEVANTAMOSELGRADODE HIPERTATICIDAD:
𝛿 =
𝜕𝑈 𝑀
𝜕𝑅
= 0 …( 𝑁𝑂 𝑃𝑅𝑂𝑉𝑂𝐶𝐴 𝑁𝐼𝑁𝐺𝑈𝑁 𝐷𝐸𝑆𝑃𝐿𝐴𝑍𝐴𝑀𝐼𝐸𝑁𝑇𝑂)
R= FUERZA REDUNDANTE

16. ECUACION DE FUERZA INTERNAS:
𝛿 =
𝜕𝑈 𝑀
𝜕𝑅
=
1
𝐸𝐼
∫ 𝑀 (
𝜕𝑀
𝜕𝐻1
) 𝑑𝑥
𝐿
0
= 0
1
𝐸𝐼
∫ 𝑀 (
𝜕𝑀
𝜕𝐻1
) 𝑑𝑥
𝐿
0
= 0
a) FUERZAS INTERNAS:
SECCION (a-a) 𝟎 ≤ 𝜽 ≤ 𝟗𝟎

17. 𝑉𝐴 = 𝜔𝑟 𝑠𝑖𝑛 𝜃 − 𝜔𝑟(1 − 𝑐𝑜𝑠 𝜃) 𝑠𝑖𝑛𝜃 − 𝜔𝑟 𝑠𝑖𝑛 𝜃 𝑐𝑜𝑠 𝜃
− 𝐻1 𝑐𝑜𝑠 𝜃
𝑉𝐴 = 𝜔𝑟 𝑐𝑜𝑠 𝜃
𝑁𝐴 = 𝜔𝑟(1 − 𝑐𝑜𝑠 𝜃) 𝑐𝑜𝑠𝜃 − 𝐻1 𝑠𝑖𝑛 𝜃 − 𝜔𝑟 𝑐𝑜𝑠 𝜃 − 𝜔𝑟 𝑠𝑖𝑛2
𝜃
𝑁𝐴 = 𝜔𝑟( 𝑠𝑖𝑛 𝜃 − 1)

18. 𝑀𝐴 = 𝜔𝑟. ( 𝑟 𝑠𝑖𝑛 𝜃) + 𝜔𝑟. 𝑟(1 − 𝑐𝑜𝑠 𝜃) − 𝜔𝑟.
𝑟
2
𝑠𝑖𝑛2
𝜃
− 𝜔𝑟.
𝑟
2
(1 − 𝑐𝑜𝑠 𝜃)2
𝑀𝐴 = 𝜔𝑟2( 𝑠𝑖𝑛 𝜃 − 1)