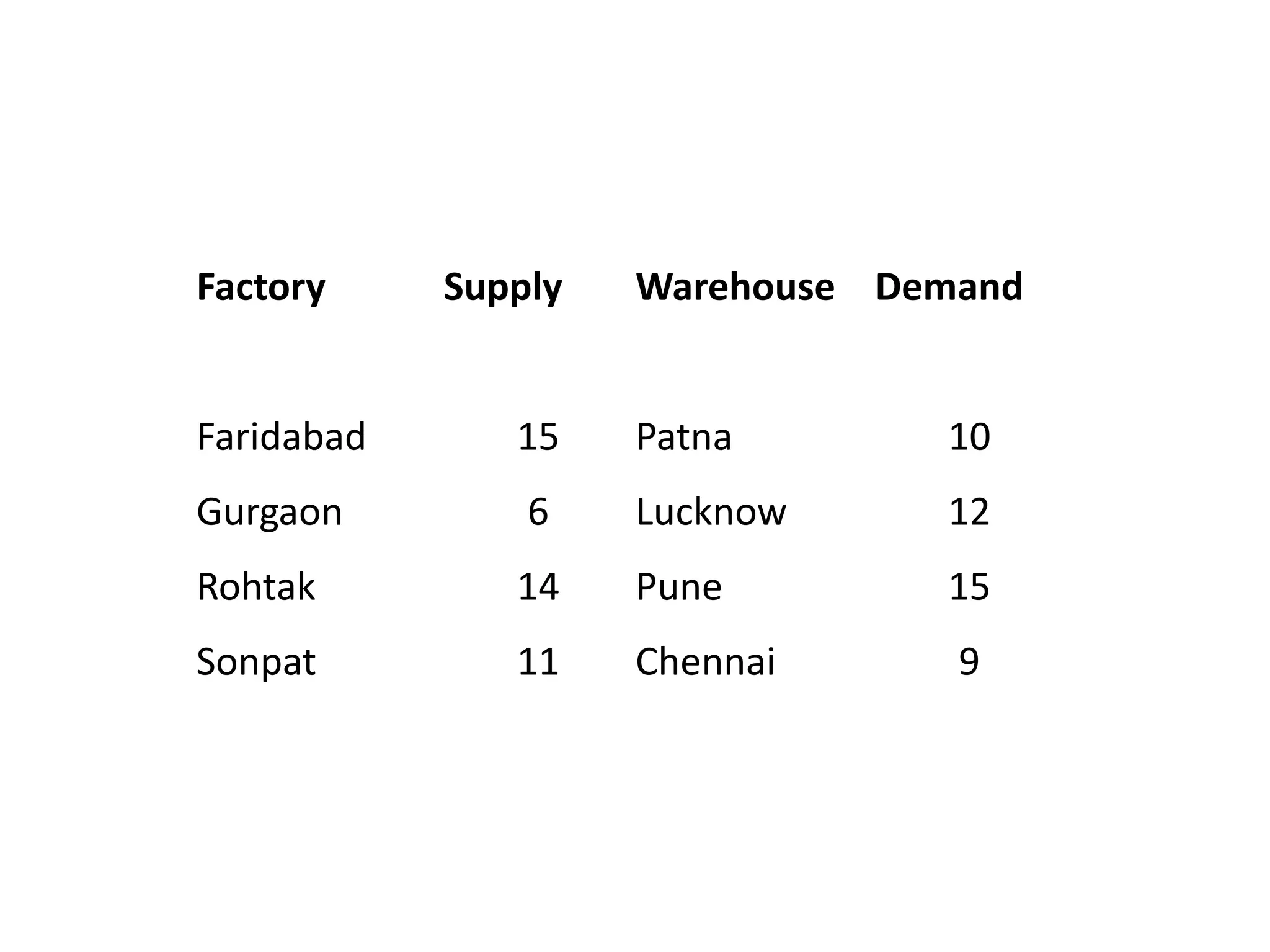
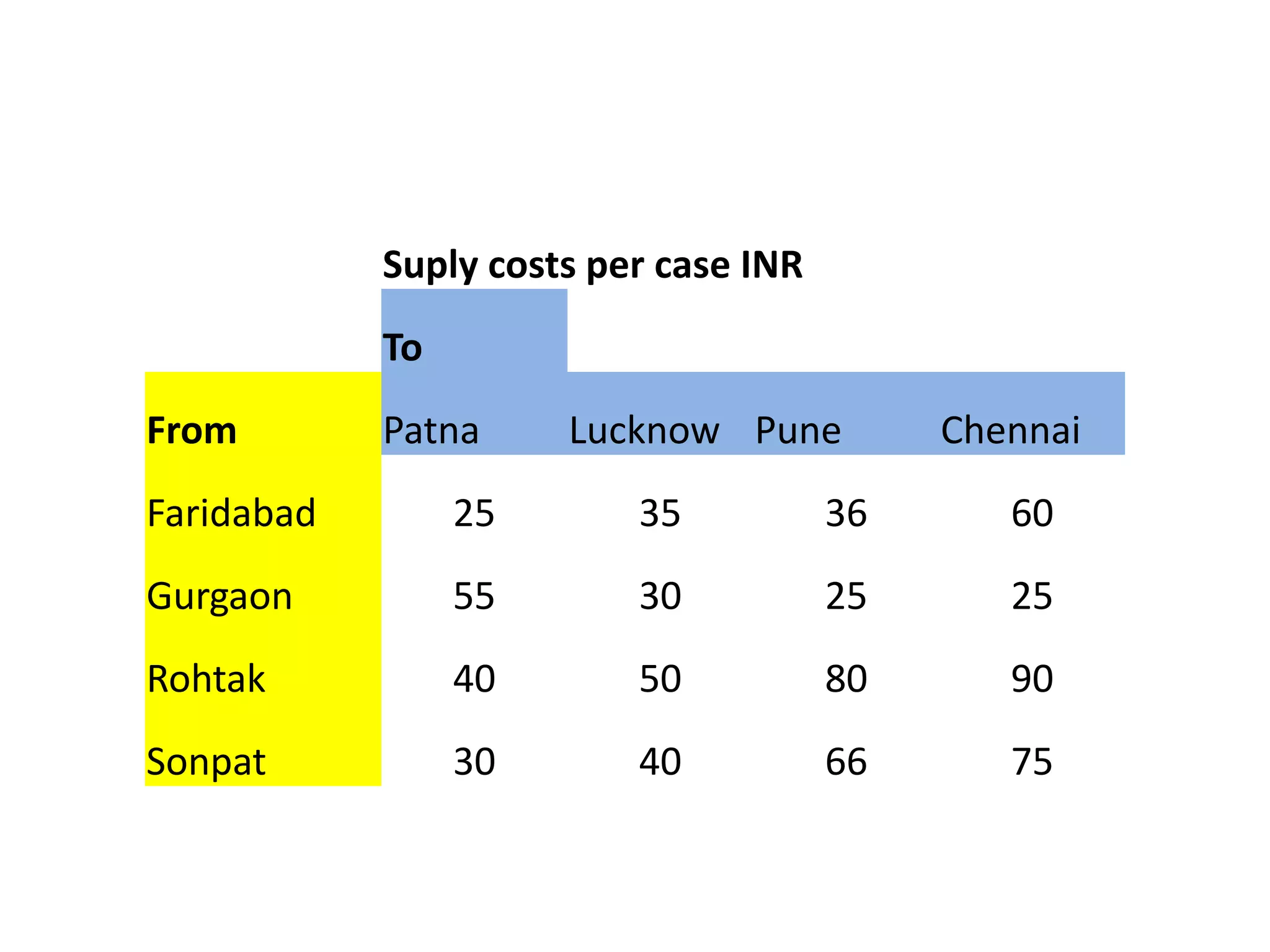
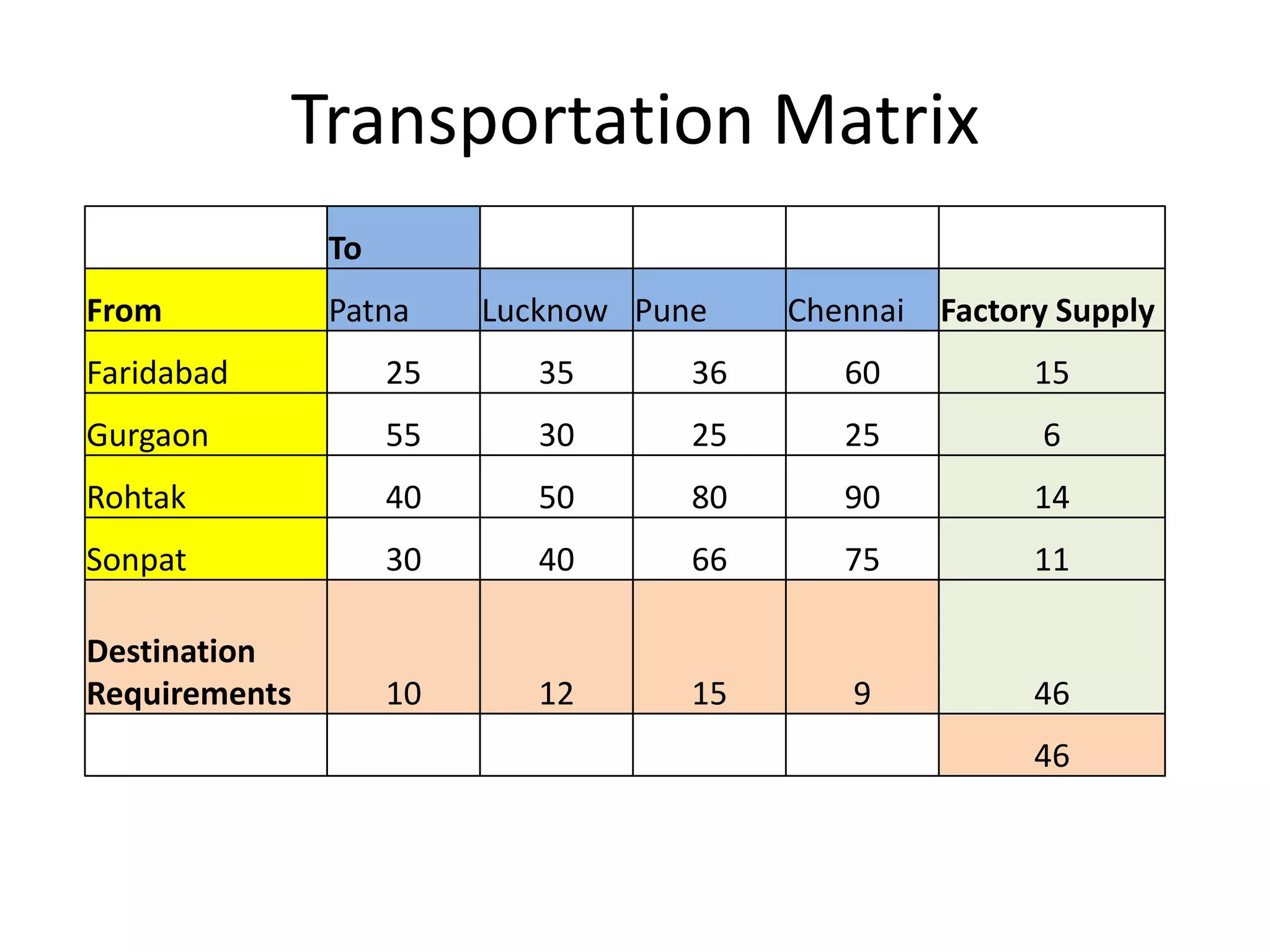
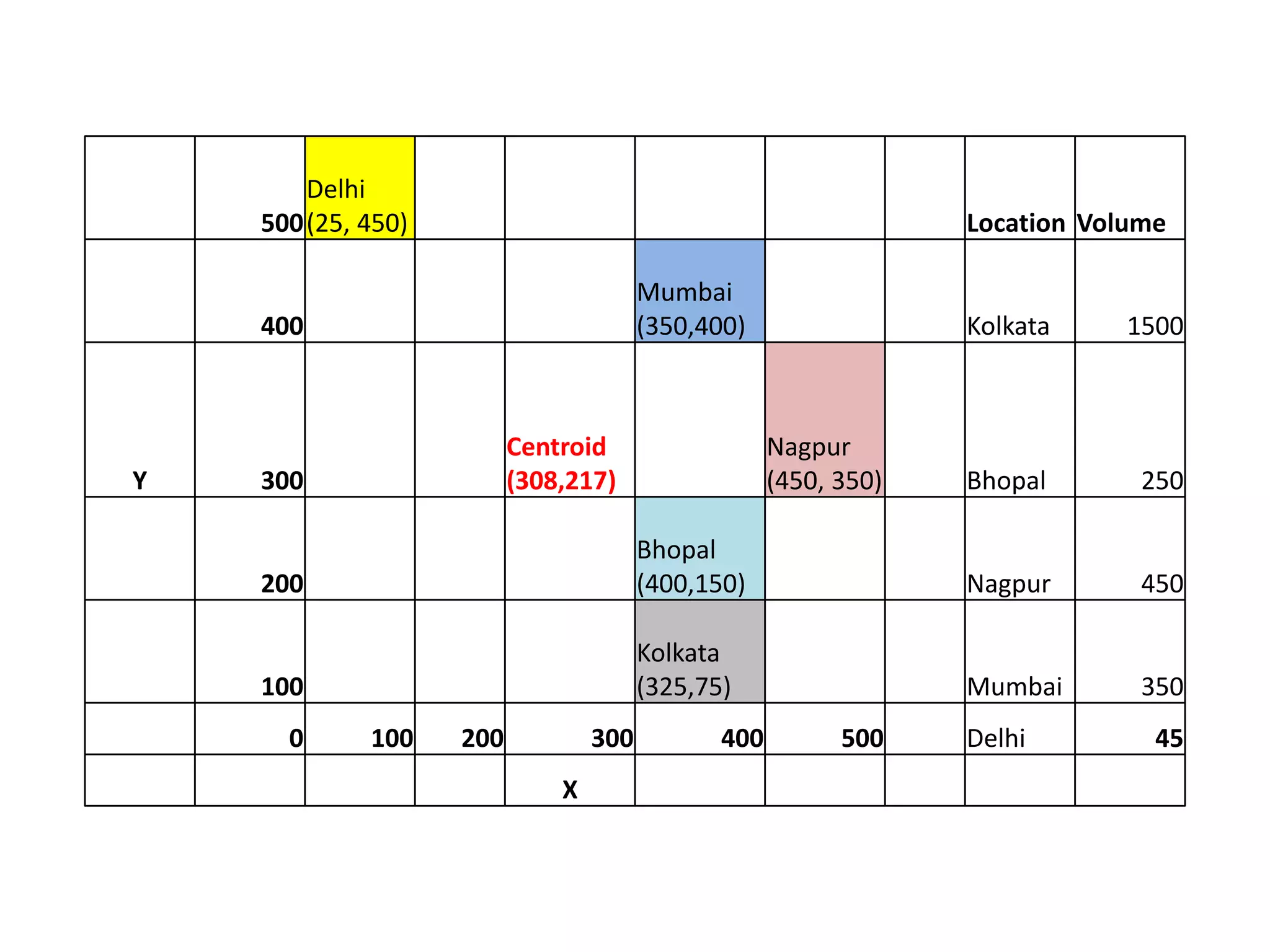
The document describes linear programming and transportation problems. It provides an example of using linear programming to optimize production at a company making hockey sticks and chess sets given machine capacity constraints. It then describes how transportation problems can be formulated as a special case of linear programming to minimize shipping costs given supply, demand, and per-unit shipping costs. The document includes a numerical example of solving a transportation problem to allocate supply across multiple destinations to meet demand at lowest cost.

1. Transportation Method
A special case of
Linear Programming

2. Linear Programming ... 1
• A method of allocating resources in an
optimum way
• A decision making tool for all industries
• A mathematical method to maximize profits of
minimize costs
• Resources are decision variables
• Objective function = criteria for selecting the
best values for these variables

3. Linear Programming ... 2
• Limitations on resource availability are called
constraints set
• Linear = the criteria for selecting the variables
can be linear
• Entire problem can be expresses as straight
lines of planes
• Non-negativity constraints

4. Linear Programming Formula
• Maximize Z = C1*X1 + C2*X2 + .... +Cn*Xn
• Subject to
– A11*X1 + A12*X2 + .... + A1n*Xn < = B1
– A21*X1 + A22*X2 + .... + A2n*Xn < = B2
– ---– ---– Am1*X1 + Am2*X2 + .... +Amn*Xn <= Bm
• C, Amn and Bm re given constraints

5. Linear Programming Example
• A company making Hockey Sticks and Chess sets
• Hockey stick profit = $2, Chess set = $4
• Hockey stick takes 4 hours and Machine A and 2
hours at Machine B
• Chess takes 6 hours at Machine A and 6 hours at
Machine B and 1 hour at Machine C
• Machine A has max 120 hours capacity per day,
Machine B has 72 hours and machine C has 10
hours

6. Formulation
• H = number of Hockey sticks and C = number
of chess sets
• Maximize Z = $2*H + $4*C
• 4*H + 6*C <= 120 (Machine A)
• 2*H + 6*C <= 72 (Machine B)
• 1*C <= 10 (Machine C)
• H , C >= 0

7. Transportation
• Special case of Linear Programming
• Maximize profits, minimize costs of shipping
• N units, M destinations

8. Factory
Supply
Warehouse Demand
Faridabad
15
Patna
10
Gurgaon
6
Lucknow
12
Rohtak
14
Pune
15
Sonpat
11
Chennai
9

9. Suply costs per case INR
To
From
Patna
Lucknow Pune
Chennai
Faridabad
25
35
36
60
Gurgaon
55
30
25
25
Rohtak
40
50
80
90
Sonpat
30
40
66
75

10. Transportation Matrix
To
From
Patna
Lucknow Pune
Chennai
Factory Supply
Faridabad
25
35
36
60
15
Gurgaon
55
30
25
25
6
Rohtak
40
50
80
90
14
Sonpat
30
40
66
75
11
Destination
Requirements
10
12
15
9
46
46

11. Centroid Method
• To locate single facility considering existing
facilities
• Based on the distance and volume
• Simplistic assumptions

12. Delhi
500 (25, 450)
Location Volume
Mumbai
(350,400)
400
Y
Kolkata
1500
Bhopal
250
200
Bhopal
(400,150)
Nagpur
450
100
Kolkata
(325,75)
Mumbai
350
Centroid
(308,217)
300
0
100
200
300
X
Nagpur
(450, 350)
400
500
Delhi
45