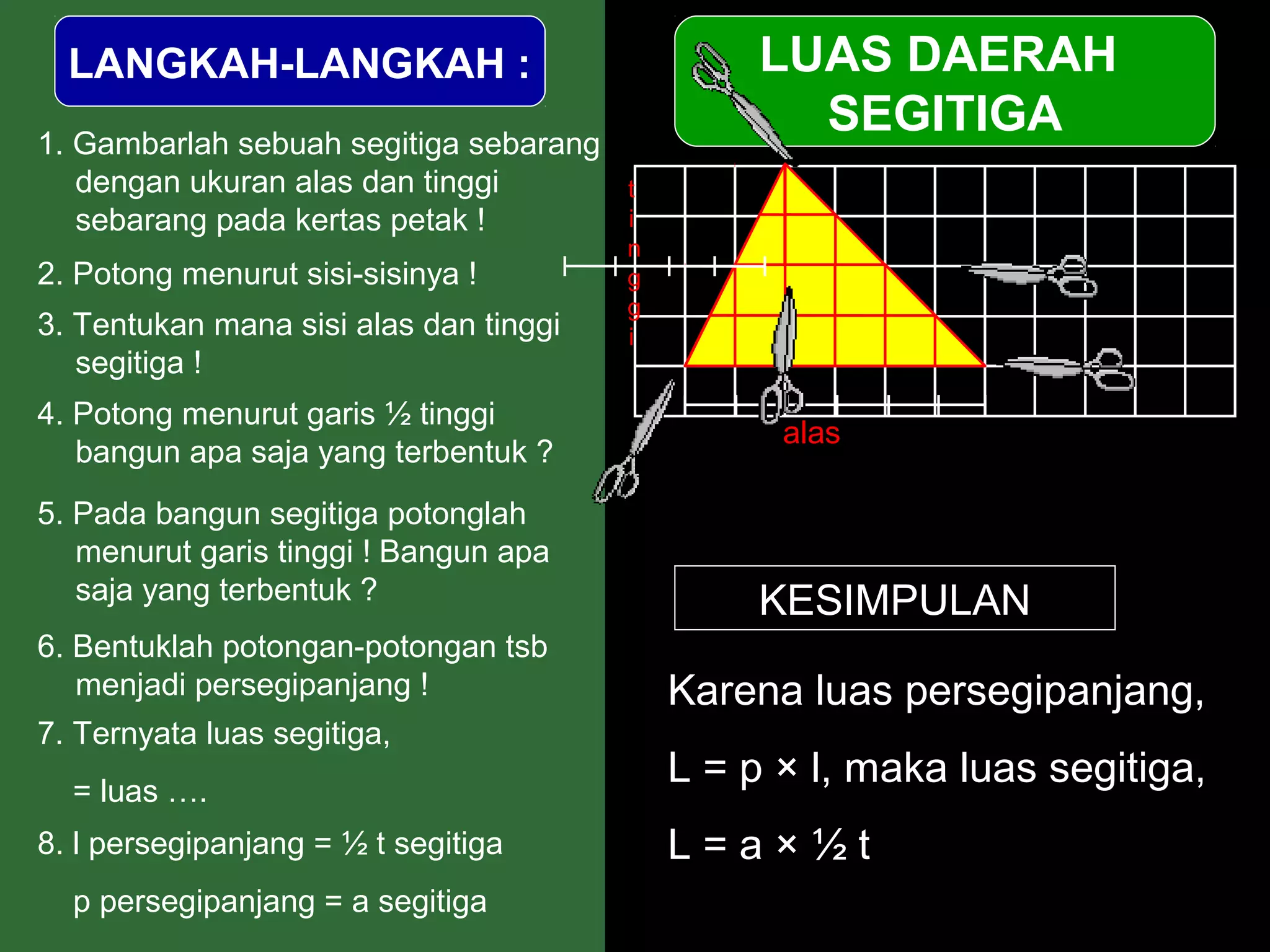
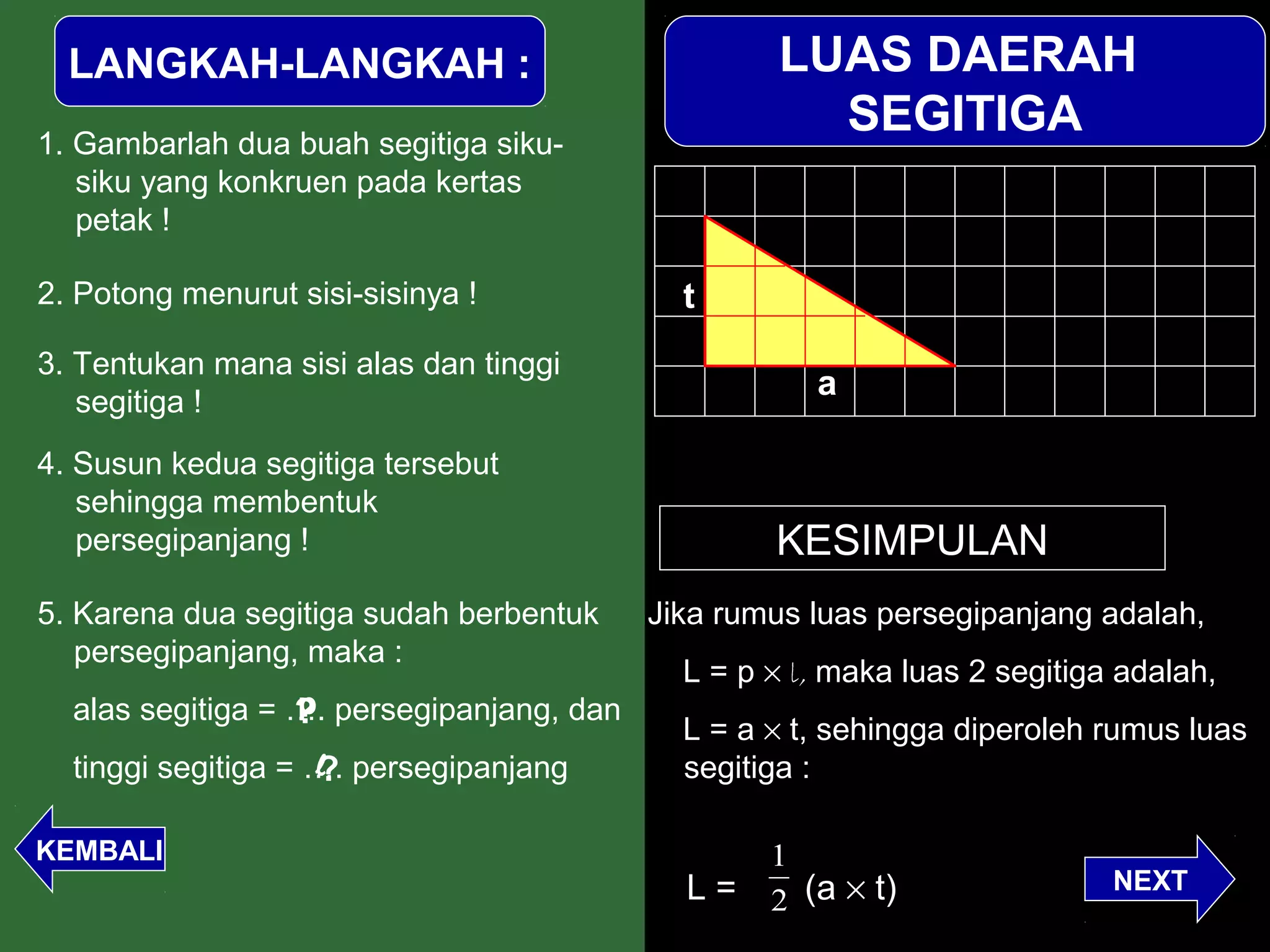
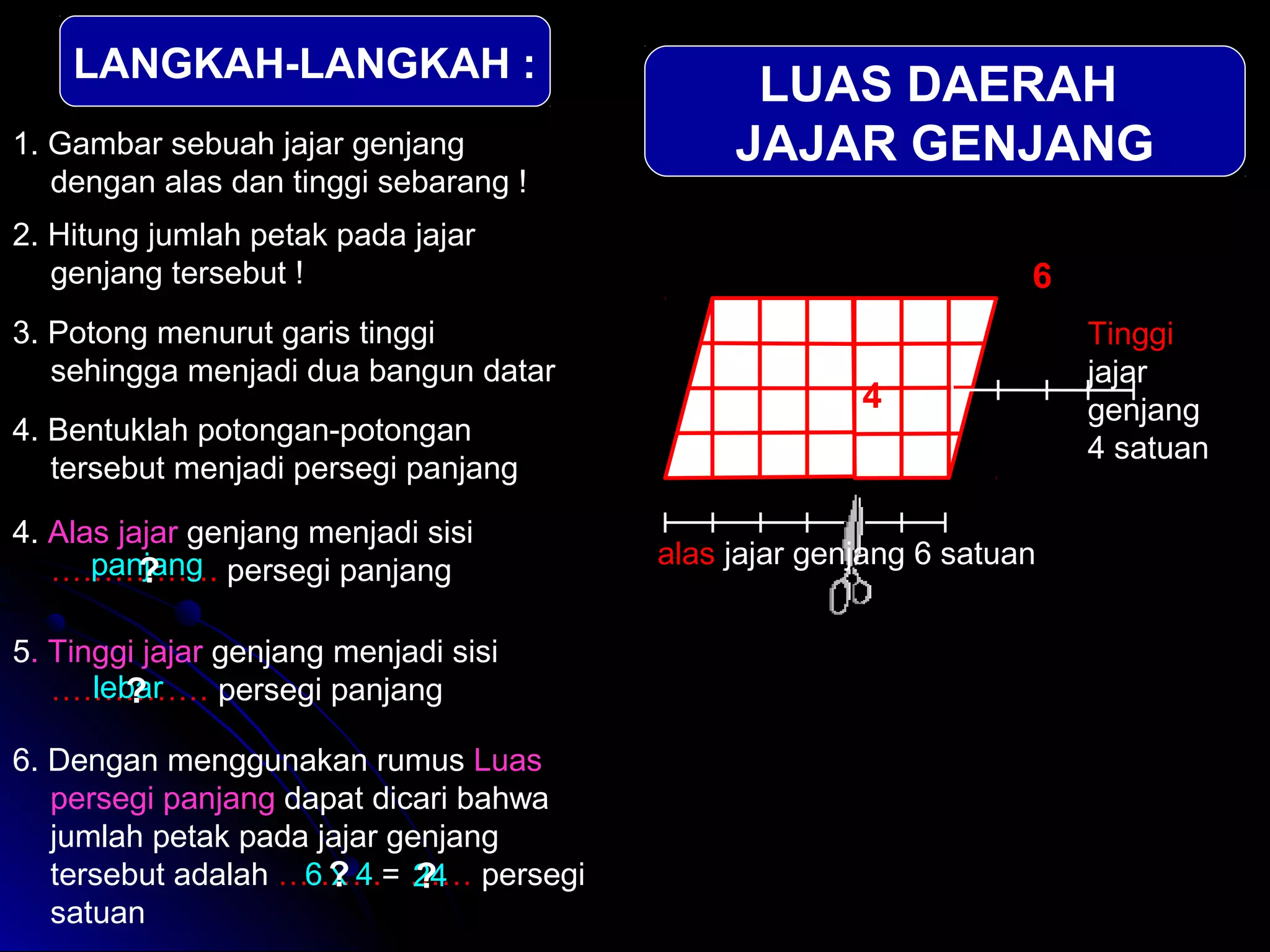
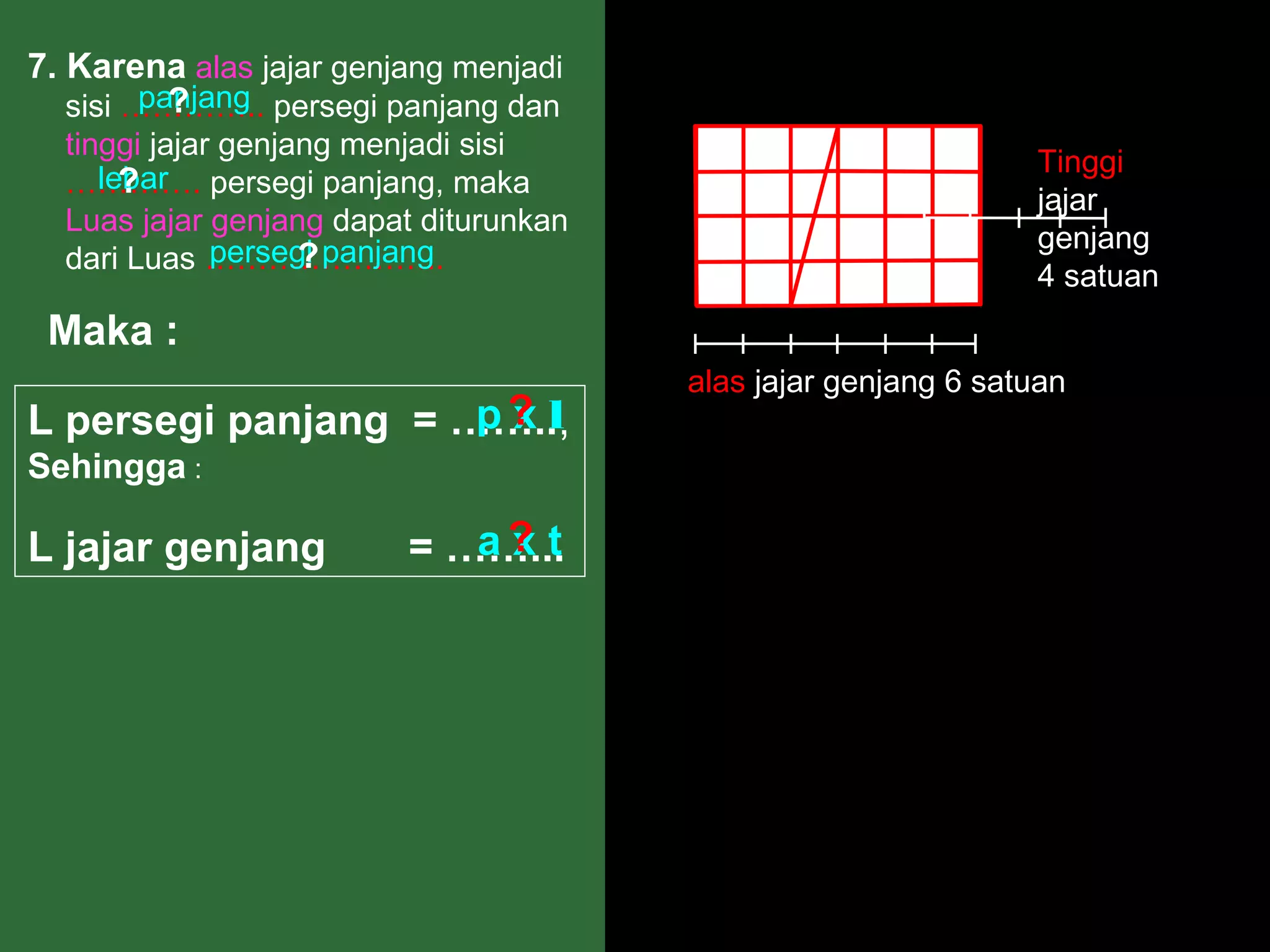
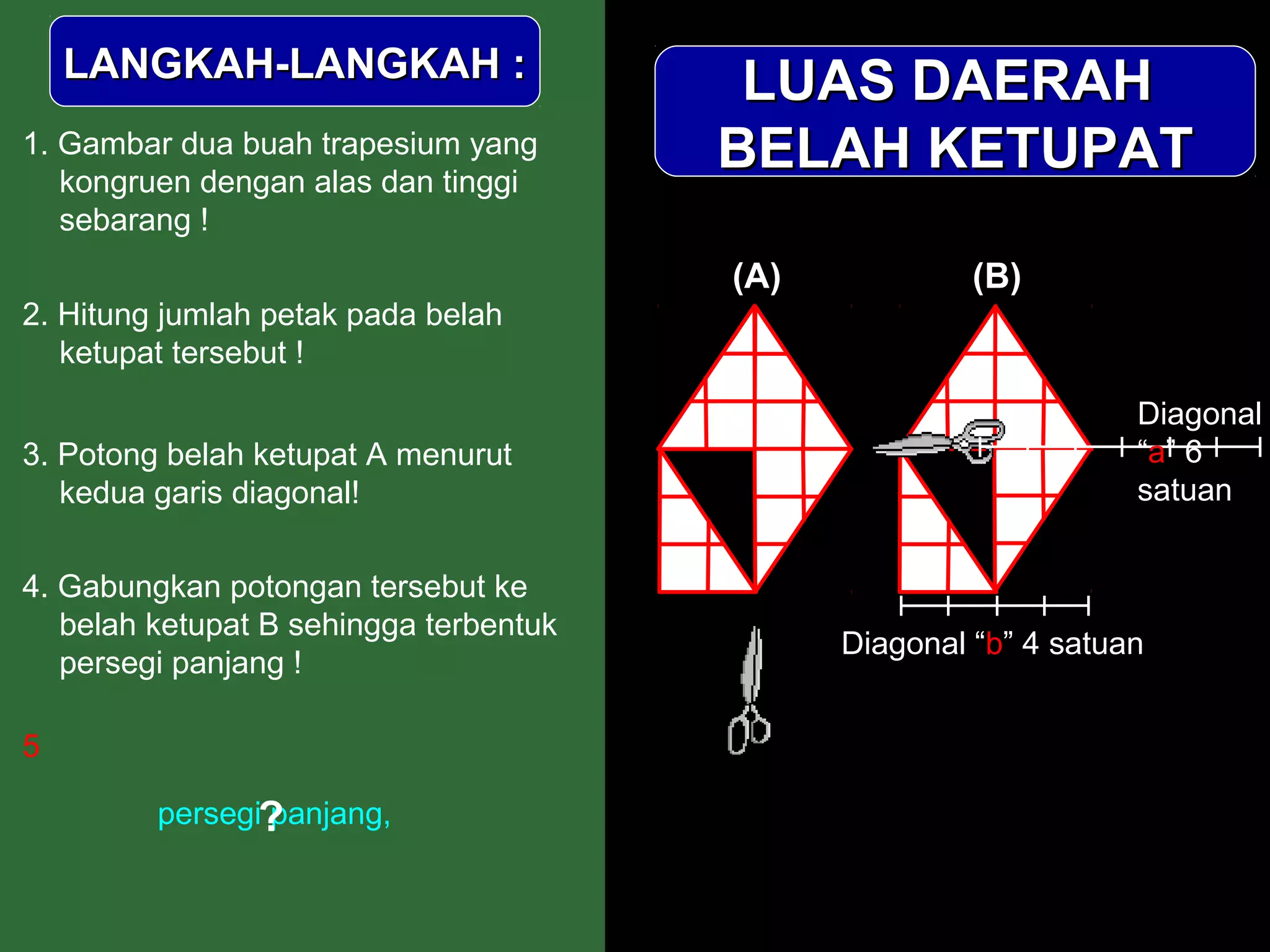
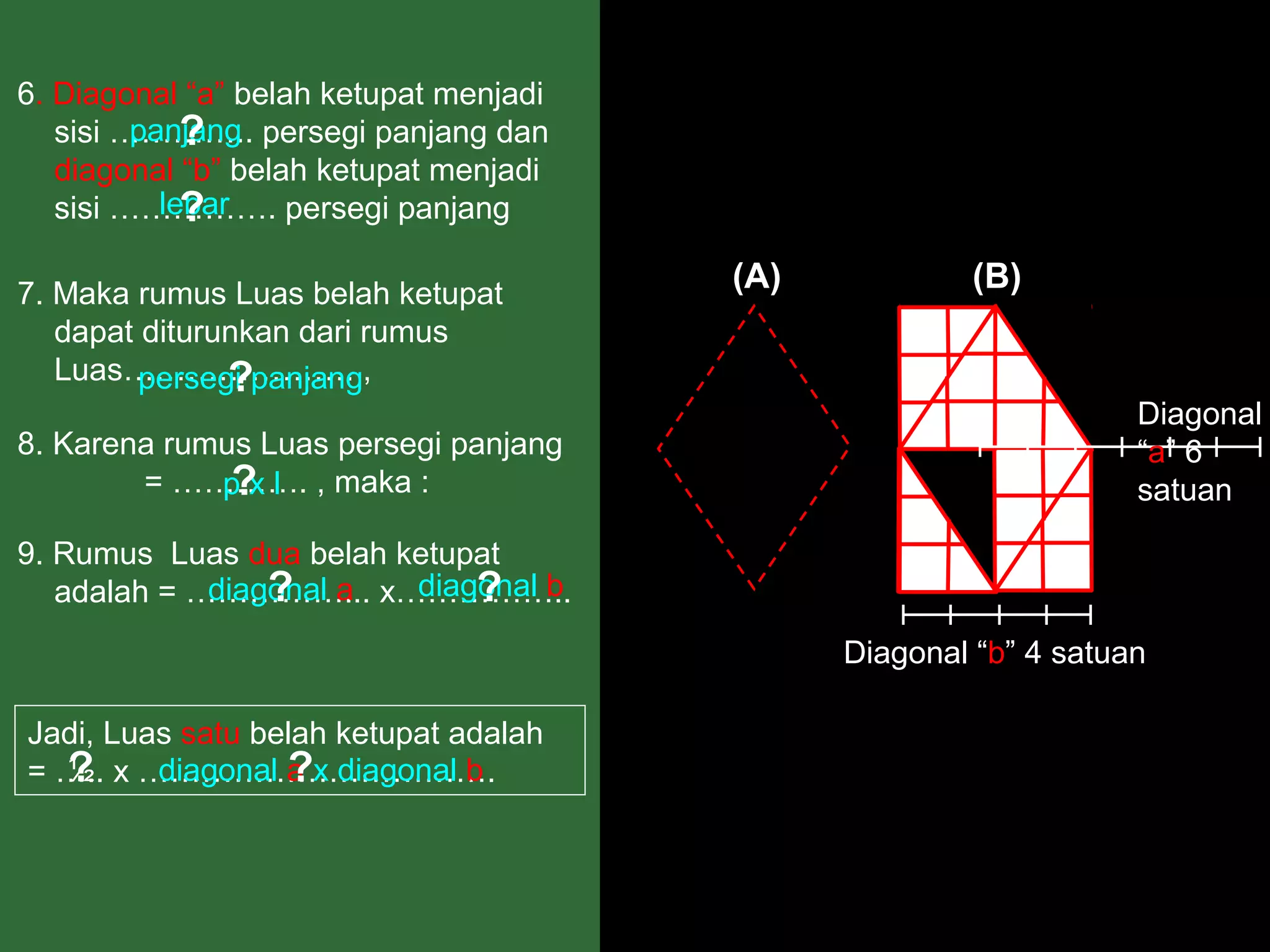
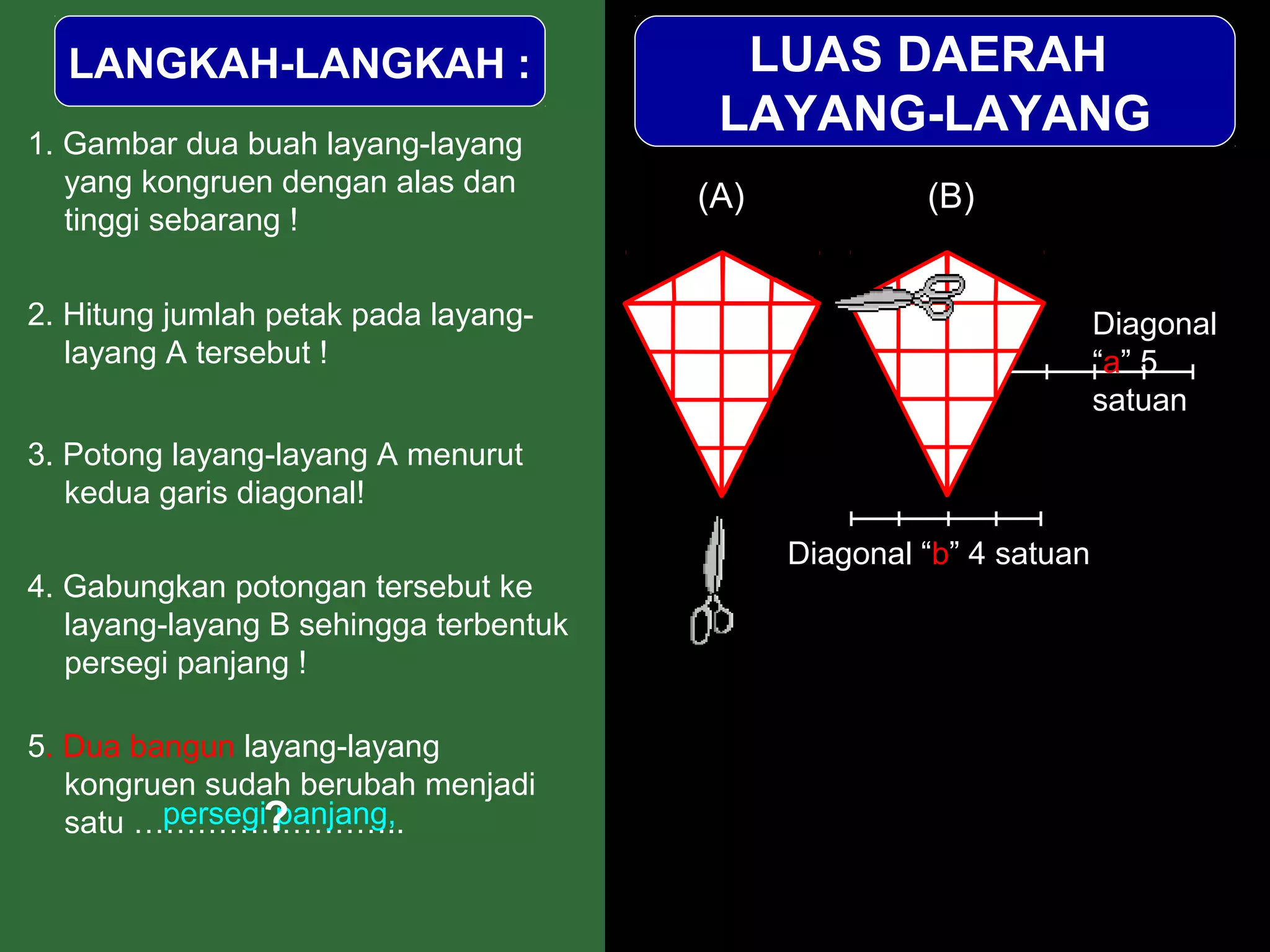
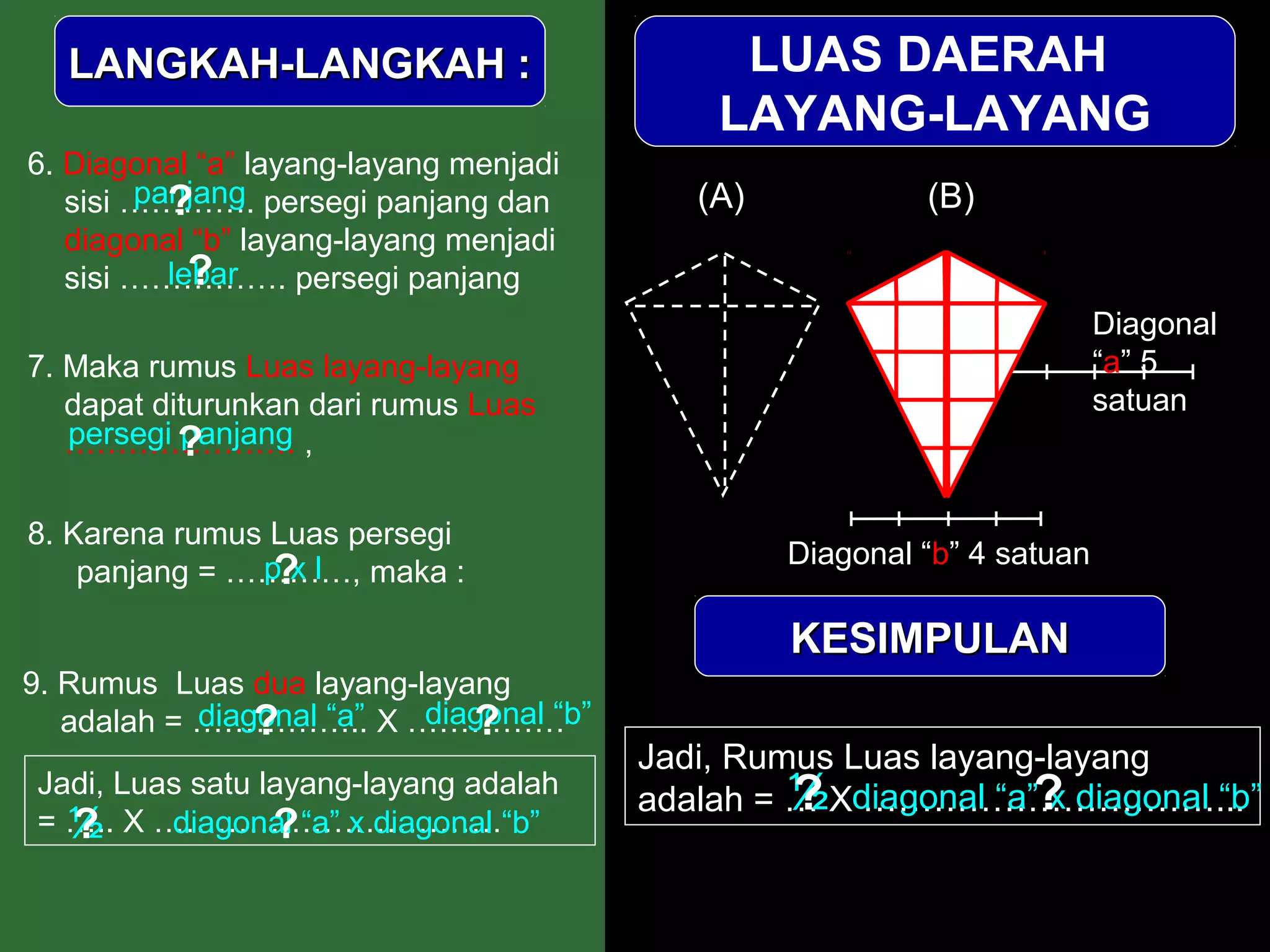
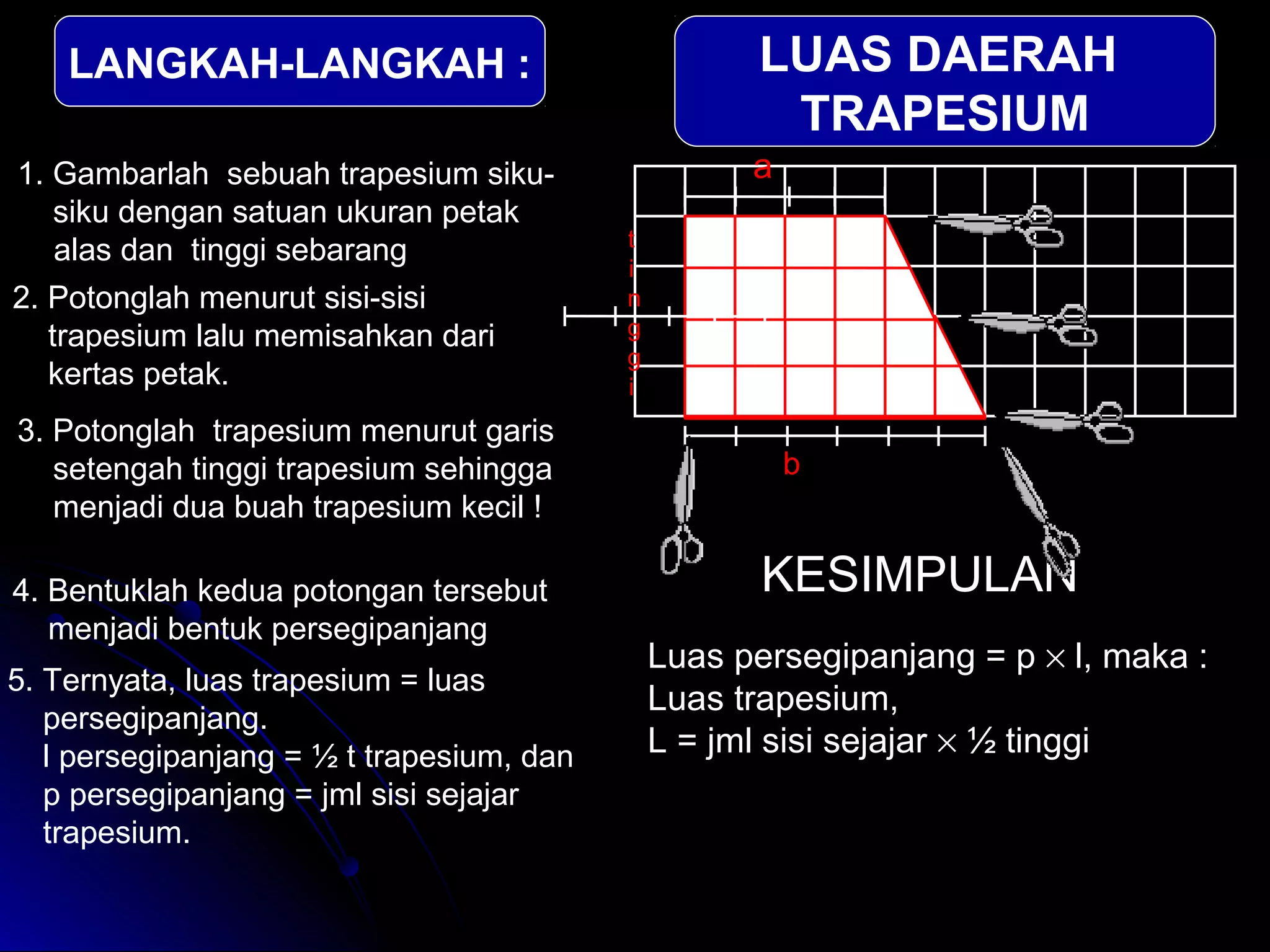
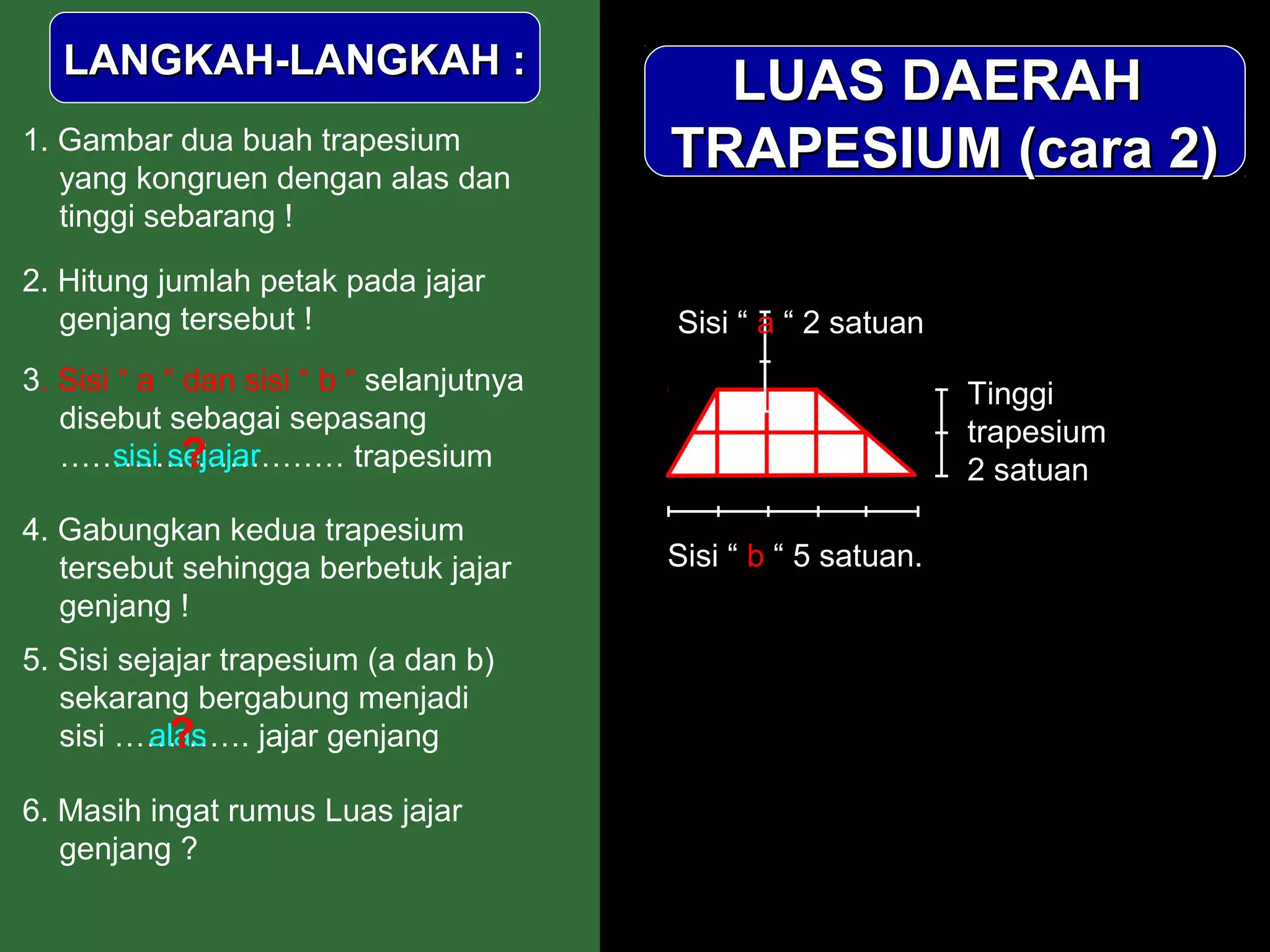
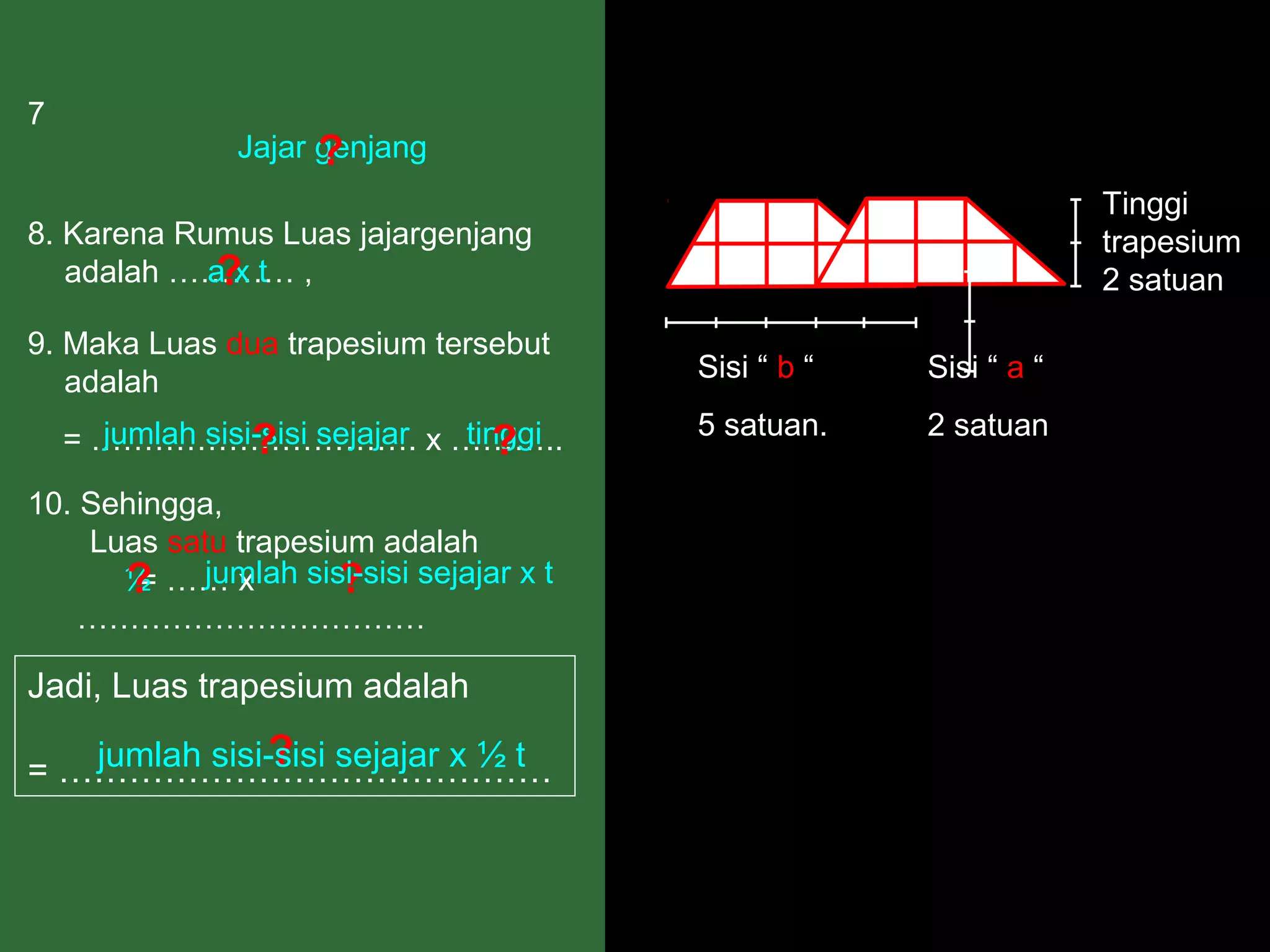
Dokumen ini menjelaskan langkah-langkah dalam menghitung luas berbagai bangun datar seperti persegipanjang, segitiga, jajar genjang, belah ketupat, layang-layang, dan trapesium. Metode ini meliputi pengamatan, pemotongan, dan penggabungan potongan untuk membentuk bangun lain guna mempermudah perhitungan luas. Kesimpulan dari setiap jenis bangun menyajikan rumus luas yang sesuai dengan prinsip geometri yang diterapkan.

1. LANGKAH-LANGKAH : LUAS DAERAH
1. Perhatikan persegipanjang dan PERSEGIPANJANG
persegi satuan berikut !
2. Tutuplah persegipanjang tersebut
dengan persegi satuan yang tersedia !
3. Berapa persegi satuan yang dapat
menutupi daerah persegipanjang
tersebut ?
4. Perhatikan lagi persegipanjang
berikut ! l
5. Tutupilah sebagian persegipanjang
yang diwakili oleh bagian salah satu p
kolom dan baris.
6. Dengan cara apa dapat menghitung
luas persegipanjang tersebut ? KESIMPULAN :
7. Jika banyak kolom adalah p dan Rumus luas daerah persegipanjang :
banyak baris adalah l, maka dapat
panjang
? ?
lebar
L = ………..... × ………..
diperoleh rumus luas
persegipanjang adalah .... p?× l
= ……………..

2. LANGKAH-LANGKAH : LUAS DAERAH
1. Perhatikan persegipanjang dan PERSEGIPANJANG
persegi satuan berikut !
2. Tutuplah persegipanjang tersebut
dengan persegi satuan yang tersedia !
3. Berapa persegi satuan yang dapat
menutupi daerah persegipanjang
tersebut ?
4. Perhatikan lagi persegipanjang
berikut ! l
5. Tutupilah sebagian persegipanjang
yang diwakili oleh bagian salah satu p
kolom dan baris.
6. Dengan cara apa dapat menghitung
luas persegipanjang tersebut ? KESIMPULAN :
7. Jika banyak kolom adalah p dan Rumus luas daerah persegipanjang :
banyak baris adalah l, maka dapat
panjang lebar
L = ………..... × ………..
diperoleh rumus luas
persegipanjang adalah .... p× l
= ……………..
BACK NEXT

3. LANGKAH-LANGKAH : LUAS DAERAH
1. Gambarlah sebuah segitiga sebarang
SEGITIGA
dengan ukuran alas dan tinggi t
sebarang pada kertas petak ! i
n
2. Potong menurut sisi-sisinya ! g
g
3. Tentukan mana sisi alas dan tinggi i
segitiga !
4. Potong menurut garis ½ tinggi
alas
bangun apa saja yang terbentuk ?
5. Pada bangun segitiga potonglah
menurut garis tinggi ! Bangun apa
saja yang terbentuk ? KESIMPULAN
6. Bentuklah potongan-potongan tsb
menjadi persegipanjang ! Karena luas persegipanjang,
7. Ternyata luas segitiga,
= luas ….
L = p × l, maka luas segitiga,
8. l persegipanjang = ½ t segitiga L=a×½t
p persegipanjang = a segitiga

4. LANGKAH-LANGKAH : LUAS DAERAH
1. Gambarlah dua buah segitiga siku-
SEGITIGA
siku yang konkruen pada kertas
petak !
2. Potong menurut sisi-sisinya ! t
3. Tentukan mana sisi alas dan tinggi
a
segitiga !
4. Susun kedua segitiga tersebut
sehingga membentuk
persegipanjang ! KESIMPULAN
5. Karena dua segitiga sudah berbentuk Jika rumus luas persegipanjang adalah,
persegipanjang, maka :
L = p × l, maka luas 2 segitiga adalah,
p
?
alas segitiga = …. persegipanjang, dan
L = a × t, sehingga diperoleh rumus luas
l
?
tinggi segitiga = …. persegipanjang segitiga :
KEMBALI 1
2 (a × t)
L= NEXT

5. LANGKAH-LANGKAH : LUAS DAERAH
1. Gambarlah dua buah segitiga siku-
SEGITIGA
siku yang konkruen pada kertas
petak !
2. Potong menurut sisi-sisinya ! t
a
3. Tentukan mana sisi alas dan tinggi
segitiga !
4 KESIMPULAN
Jika rumus luas persegipanjang adalah,
L = p × l, maka luas 2 segitiga adalah,
5. Karena dua segitiga sudah berbentuk
L = a × t, sehingga diperoleh rumus luas
persegipanjang, maka :
segitiga :
p
?
alas segitiga = …. persegipanjang, dan
l
?
tinggi segitiga = …. persegipanjang 1
L= 2 (a × t)

6. LANGKAH-LANGKAH :
LUAS DAERAH
1. Gambar sebuah jajar genjang JAJAR GENJANG
dengan alas dan tinggi sebarang !
2. Hitung jumlah petak pada jajar
genjang tersebut ! 6
3. Potong menurut garis tinggi Tinggi
sehingga menjadi dua bangun datar jajar
4 genjang
4. Bentuklah potongan-potongan
4 satuan
tersebut menjadi persegi panjang
4. Alas jajar genjang menjadi sisi
panjang alas jajar genjang 6 satuan
?
……………. persegi panjang
5. Tinggi jajar genjang menjadi sisi
lebar
?
…………… persegi panjang
6. Dengan menggunakan rumus Luas
persegi panjang dapat dicari bahwa
jumlah petak pada jajar genjang
6 ? 4 24 ?
tersebut adalah ……….= …… persegi
x
satuan

7. 7. Karena alas jajar genjang menjadi
panjang
?
sisi ………….. persegi panjang dan
tinggi jajar genjang menjadi sisi
Tinggi
lebar
?
…………. persegi panjang, maka
jajar
Luas jajar genjang dapat diturunkan
persegi panjang genjang
?
dari Luas …………………..
4 satuan
Maka :
alas jajar genjang 6 satuan
p? l
x
L persegi panjang = ……..,
Sehingga :
L jajar genjang a? t
x
= ……...

8. LANGKAH-LANGKAH :
LUAS DAERAH
1. Gambar dua buah trapesium yang
kongruen dengan alas dan tinggi
BELAH KETUPAT
sebarang !
(A) (B)
2. Hitung jumlah petak pada belah
ketupat tersebut !
Diagonal
3. Potong belah ketupat A menurut “a” 6
kedua garis diagonal! satuan
4. Gabungkan potongan tersebut ke
belah ketupat B sehingga terbentuk
Diagonal “b” 4 satuan
persegi panjang !
5
persegi?
panjang,

9. 6. Diagonal “a” belah ketupat menjadi
?
panjang
sisi ………….. persegi panjang dan
diagonal “b” belah ketupat menjadi
?
lebar
sisi ……………. persegi panjang
7. Maka rumus Luas belah ketupat
(A) (B)
dapat diturunkan dari rumus
Luas…………………. ,
?
persegi panjang
Diagonal
8. Karena rumus Luas persegi panjang “a” 6
?
pxl
= …………. , maka : satuan
9. Rumus Luas dua belah ketupat
?
diagonal a ?
diagonal b
adalah = ……………... x……………..
Diagonal “b” 4 satuan
Jadi, Luas satu belah ketupat adalah
?
½ ?
diagonal a x diagonal b
= ….. x …………………………….

10. LANGKAH-LANGKAH : LUAS DAERAH
1. Gambar dua buah layang-layang
LAYANG-LAYANG
yang kongruen dengan alas dan (A) (B)
tinggi sebarang !
2. Hitung jumlah petak pada layang- Diagonal
layang A tersebut ! “a” 5
satuan
3. Potong layang-layang A menurut
kedua garis diagonal!
Diagonal “b” 4 satuan
4. Gabungkan potongan tersebut ke
layang-layang B sehingga terbentuk
persegi panjang !
5. Dua bangun layang-layang
kongruen sudah berubah menjadi
persegi?
panjang,
satu ……………………..

11. LANGKAH-LANGKAH : LUAS DAERAH
LAYANG-LAYANG
6. Diagonal “a” layang-layang menjadi
panjang
?
sisi …………. persegi panjang dan (A) (B)
diagonal “b” layang-layang menjadi
?
lebar
sisi ……………. persegi panjang
Diagonal
7. Maka rumus Luas layang-layang “a” 5
dapat diturunkan dari rumus Luas satuan
persegi ?
panjang
…………………. ,
8. Karena rumus Luas persegi
Diagonal “b” 4 satuan
?
pxl
panjang = …………, maka :
KESIMPULAN
9. Rumus Luas dua layang-layang
?
diagonal “a” diagonal “b”
adalah = …………….. X …………… ?
Jadi, Rumus Luas layang-layang
Jadi, Luas satu layang-layang adalah ½ …………………………...
adalah = … Xdiagonal “a”? diagonal “b”
? x
½
? ?
= ….. X ……………………………“b”
diagonal “a” x diagonal

12. LANGKAH-LANGKAH : LUAS DAERAH
TRAPESIUM
1. Gambarlah sebuah trapesium siku- a
siku dengan satuan ukuran petak
t
alas dan tinggi sebarang
i
2. Potonglah menurut sisi-sisi n
trapesium lalu memisahkan dari g
g
kertas petak. i
3. Potonglah trapesium menurut garis
setengah tinggi trapesium sehingga b
menjadi dua buah trapesium kecil !
4. Bentuklah kedua potongan tersebut KESIMPULAN
menjadi bentuk persegipanjang
Luas persegipanjang = p × l, maka :
5. Ternyata, luas trapesium = luas
Luas trapesium,
persegipanjang.
l persegipanjang = ½ t trapesium, dan L = jml sisi sejajar × ½ tinggi
p persegipanjang = jml sisi sejajar
trapesium.

13. LANGKAH-LANGKAH :
LUAS DAERAH
1. Gambar dua buah trapesium
yang kongruen dengan alas dan
TRAPESIUM (cara 2)
tinggi sebarang !
2. Hitung jumlah petak pada jajar
genjang tersebut ! Sisi “ a “ 2 satuan
3. Sisi “ a “ dan sisi “ b “ selanjutnya Tinggi
disebut sebagai sepasang trapesium
?
sisi sejajar
……………………… trapesium 2 satuan
4. Gabungkan kedua trapesium
tersebut sehingga berbetuk jajar Sisi “ b “ 5 satuan.
genjang !
5. Sisi sejajar trapesium (a dan b)
sekarang bergabung menjadi
?
alas
sisi …………. jajar genjang
6. Masih ingat rumus Luas jajar
genjang ?

14. 7
?
Jajar genjang
Tinggi
8. Karena Rumus Luas jajargenjang trapesium
?
axt
adalah ………… , 2 satuan
9. Maka Luas dua trapesium tersebut
adalah Sisi “ b “ Sisi “ a “
5 satuan. 2 satuan
?
jumlah sisi-sisi sejajar
= …………………………. x ……….. tinggi
?
10. Sehingga,
Luas satu trapesium adalah
? jumlah sisi-sisi sejajar x t
½ …… x
= ?
……………………………
Jadi, Luas trapesium adalah
?
jumlah sisi-sisi sejajar x ½ t
= ……………………………………