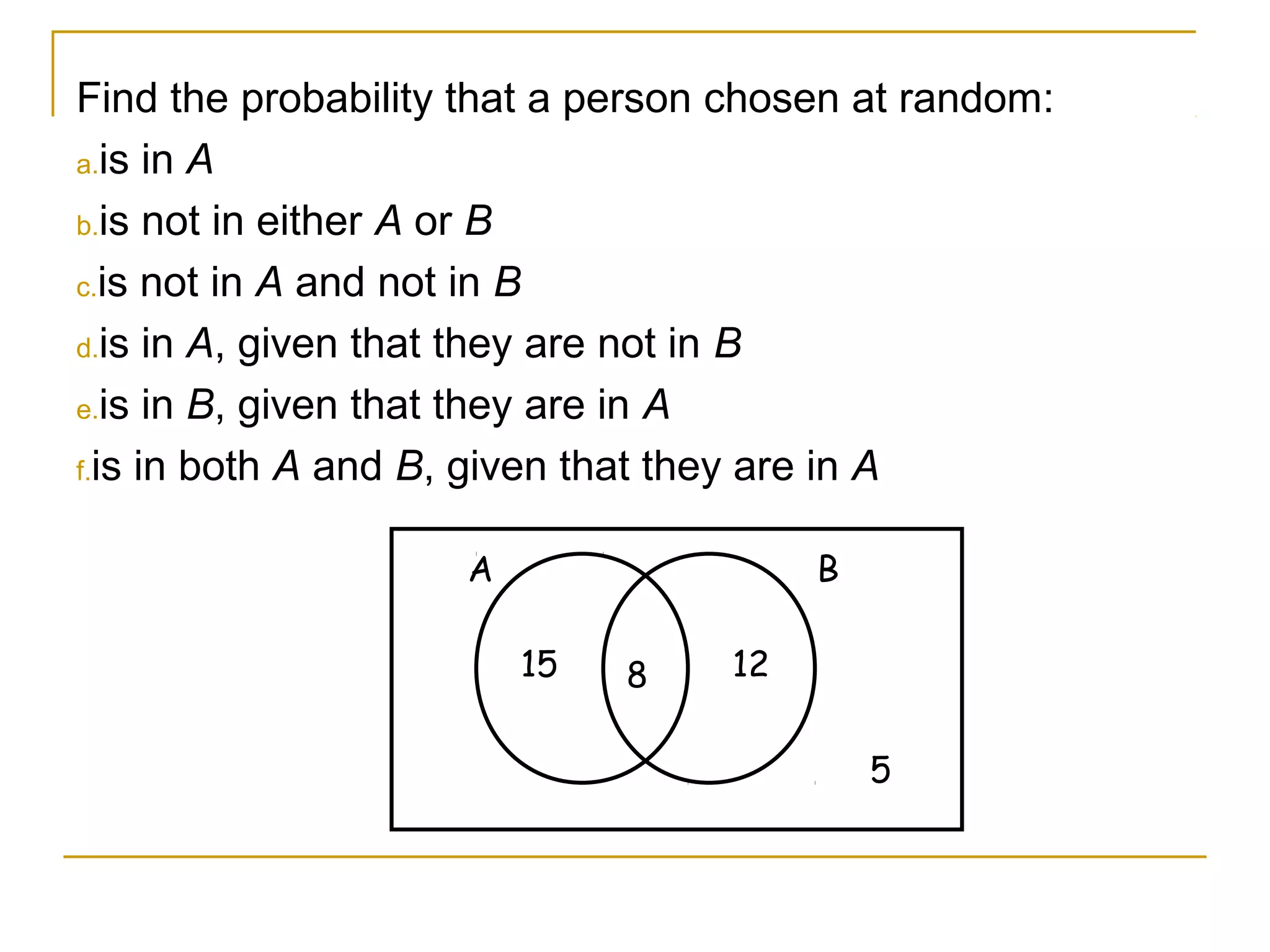
Conditional probability describes the probability of an event occurring given that another event has occurred. It is calculated as the probability of the events intersecting (both occurring) divided by the probability of the conditioning event. Venn diagrams can be used to visualize sample spaces and intersections of events to calculate conditional probabilities. Conditional probabilities limit the sample space based on a specified condition.

1. Conditional Probability
Math Studies
Diploma Programme

2. Conditional Probability
 Conditional Probability contains a condition
that may limit the sample space for an event.
 You can write a conditional probability using
the notation
P ( B A)
- This reads “the probability of event B, given
event A”

3. Conditional Probability
The table shows the results of a class survey.
Find P(own a pet | female)
Do you own a pet?
yes no
female 8 6 14 females;
male 5 7 13 males
The condition female limits the sample space to 14 possible outcomes.
Of the 14 females, 8 own a pet.
Therefore, P(own a pet | female) equals 8 .
14

4. Conditional Probability
The table shows the results of a class survey.
Find P(wash the dishes | male)
Did you wash the dishes last night?
yes no
female 7 6 13 females;
male 7 8 15 males
The condition male limits the sample space to 15 possible outcomes.
Of the 15 males, 7 did the dishes.
Therefore, P(wash the dishes | male) 7
15

5. Let’s Try One
Using the data in the table, find the probability that a sample of not
recycled waste was plastic. P(plastic | non-recycled)
The given condition limits the Material Recycled Not Recycled
sample space to non-recycled Paper 34.9 48.9
waste. Metal 6.5 10.1
Glass 2.9 9.1
A favorable outcome is
Plastic 1.1 20.4
non-recycled plastic.
Other 15.3 67.8
20.4
P(plastic | non-recycled) =
48.9 + 10.1 + 9.1 + 20.4 + 67.8
20.4
=
156.3
0.13
The probability that the non-recycled waste was plastic is about 13%.

6. Conditional Probability Formula
 The conditional probability that A occurs given
that B has occurred is written as P(A B)
and is defined as:
P(A ∩ B)
P(A B) =
P(B)

7. Problem Solving with Venn Diagram
In a class of 29 students, 20 students study French, 15
students study Malay, and 8 students study both
languages. A student is chosen at random from the class.
Find the probability that the students:
a.Studies French
b.Studies neither language
c.Studies at least one language
d.Studies both languages
e.Studies Malay given that they study French
f.Studies French given that they study Malay
g.Studies both language given that they study at least one
of the languages

8. Venn Diagram
F M
12 7
8
2

9. Find the probability that a person chosen at random:
a.is in A
b.is not in either A or B
c.is not in A and not in B
d.is in A, given that they are not in B
e.is in B, given that they are in A
f.is in both A and B, given that they are in A
A B
15 8 12
5

10. Find the probability that a person chosen at random:
a.is in A
b.is not in either A or B
c.is not in A and not in B
d.is in A, given that they are not in B
e.is in B, given that they are in A
f.is in both A and B, given that they are in A
A B
15 8 12
5