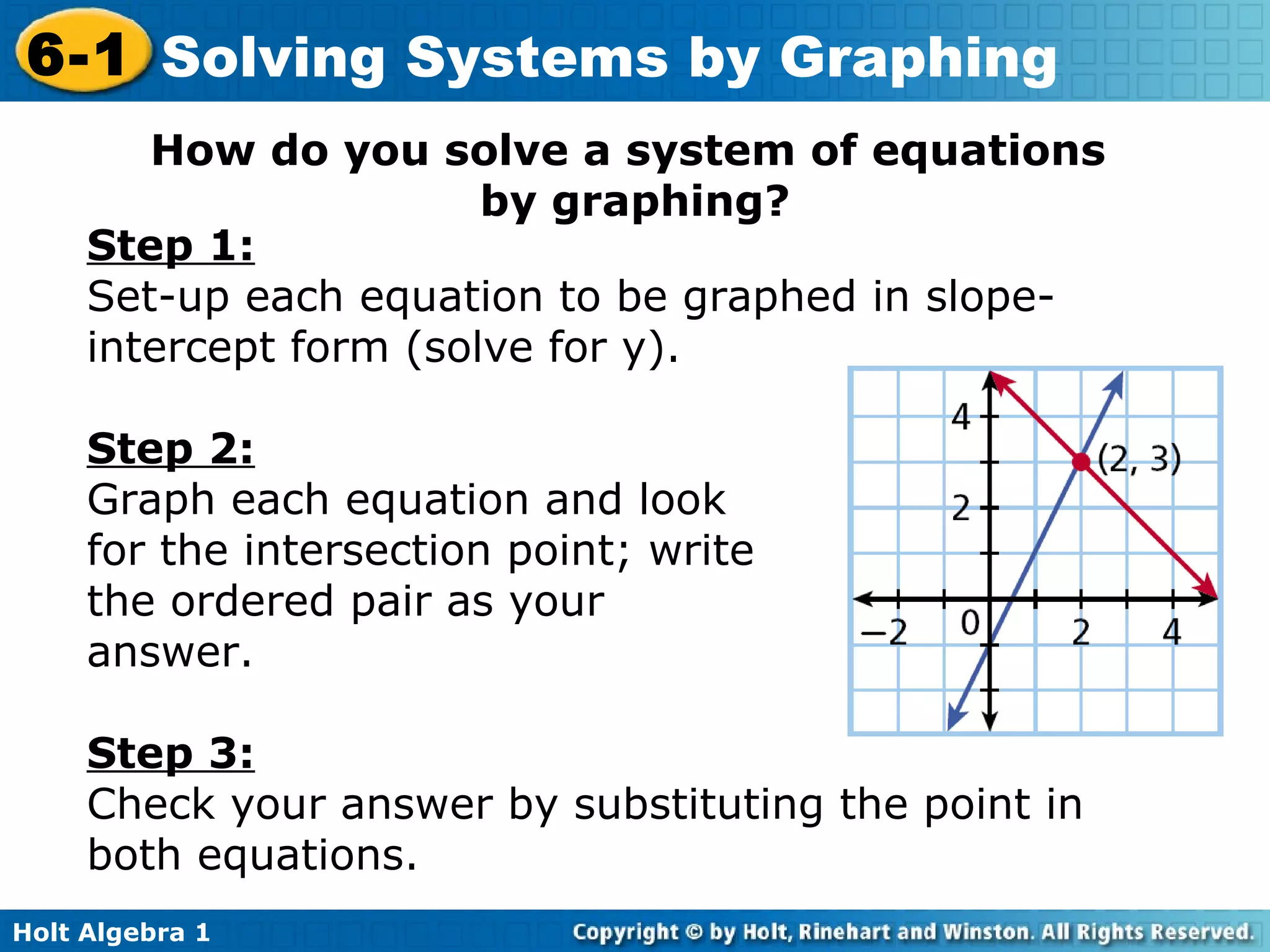
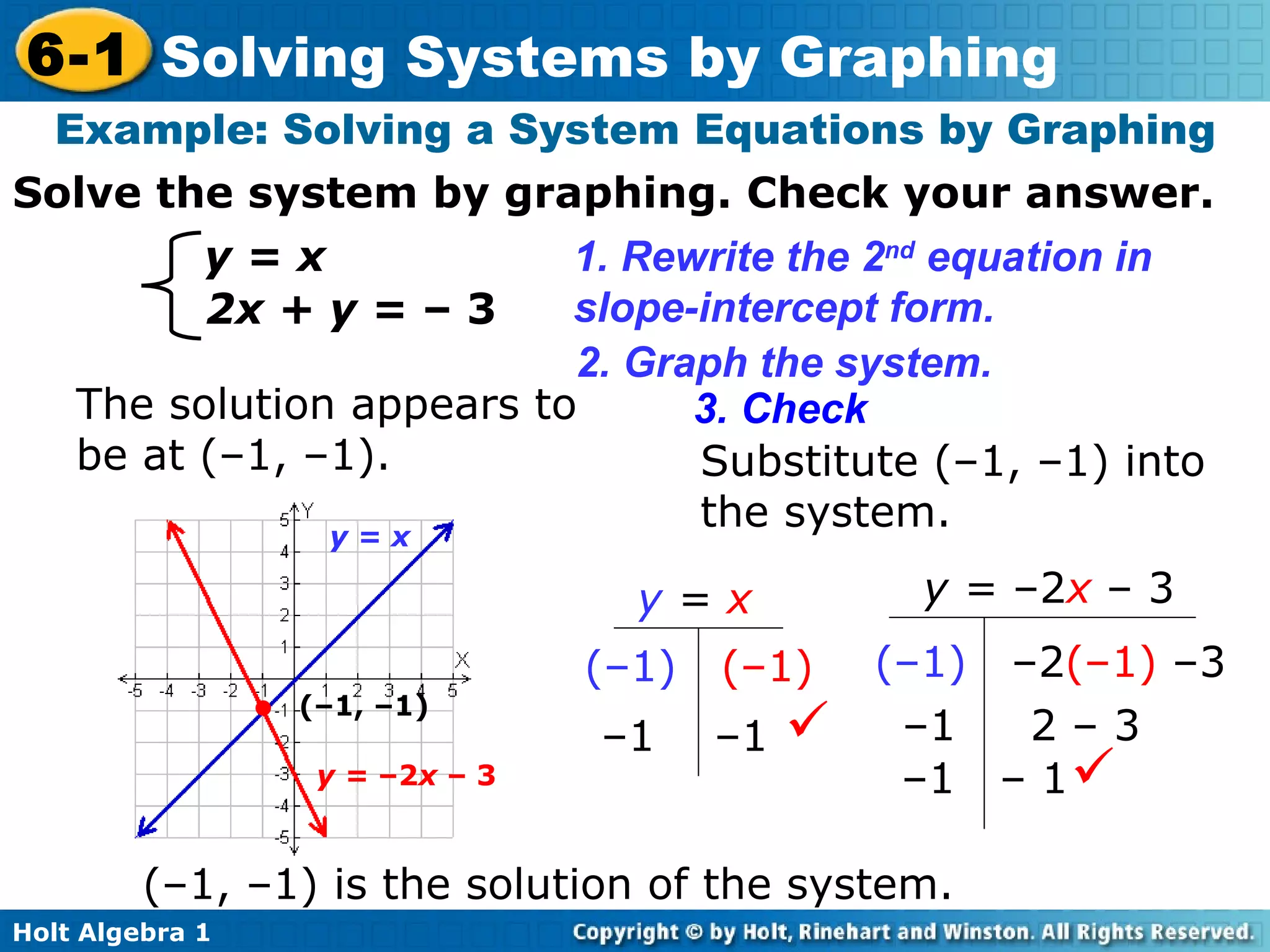
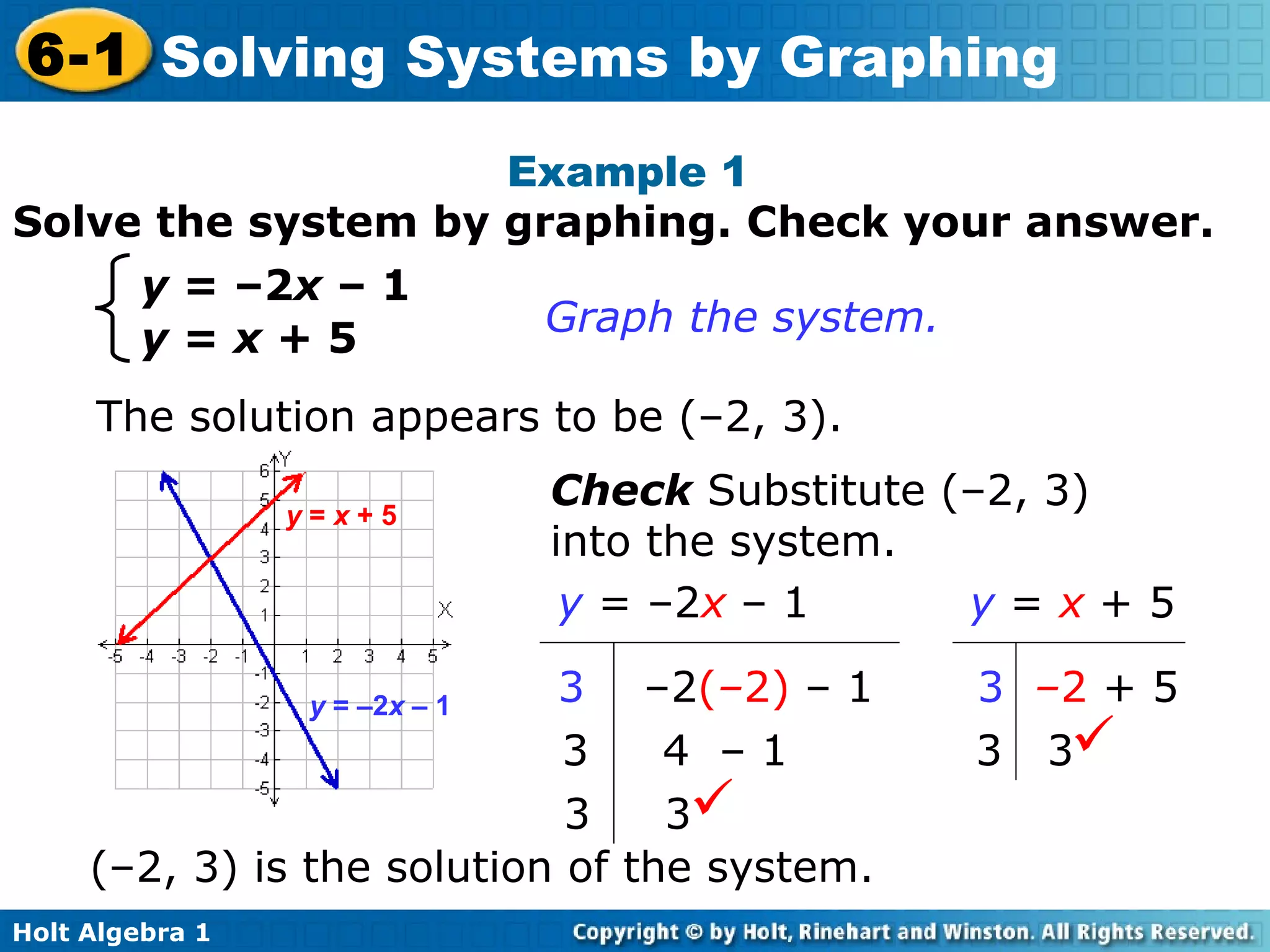
The document defines key terms related to systems of linear equations, including the definition of a system of linear equations as a set of two or more linear equations containing two or more variables. It explains that the solution of a system is an ordered pair that satisfies each equation in the system. Several methods for solving systems are described, including substitution and graphing. Graphing involves setting each equation equal to y and finding the point of intersection of the two lines. Examples are provided to illustrate identifying solutions and solving systems by graphing and checking solutions by substitution.

1. Vocabulary 3 x – y = 13 Systems Notation: A brace indicates that the equations are to be treated as a system. Ex. Word Definition System of Linear Equations A set of two or more linear equations containing 2 or more variables. Solution of a System of Linear Equations An ordered pair that satisfies each equation in the system, i.e., if an ordered pair is a solution, it will make both equations true.

2. If an ordered pair does not satisfy the first equation in the system, there is no reason to check the other equations. Helpful Hint

3. Example 1B: Identifying Systems of Solutions Tell whether the ordered pair is a solution of the given system. (–2, 2); x + 3 y = 4 – x + y = 2 Substitute –2 for x and 2 for y in each equation in the system. The ordered pair (–2, 2) makes one equation true but not the other. (–2, 2) is not a solution of the system.  – 2 + 3 (2) 4 x + 3 y = 4 – 2 + 6 4 4 4 – x + y = 2 – (–2) + 2 2 4 2

4. All solutions of a linear equation are on its graph. To find a solution of a system of linear equations, you need a point that each line has in common. In other words, you need their point of intersection . The point (2, 3) is where the two lines intersect and is a solution of both equations, so (2, 3) is the solution of the systems. y = 2 x – 1 y = – x + 5

5. How do you solve a system of equations by graphing? Step 1: Set-up each equation to be graphed in slope-intercept form (solve for y). Step 2: Graph each equation and look for the intersection point; write the ordered pair as your answer. Step 3: Check your answer by substituting the point in both equations.

6. Solve the system by graphing. Check your answer. Example: Solving a System Equations by Graphing y = x 2x + y = – 3 1. Rewrite the 2 nd equation in slope-intercept form. The solution appears to be at (–1, –1). (–1, –1) is the solution of the system. y = x y = –2 x – 3 • (–1, –1) 2. Graph the system. 3. Check Substitute (–1, –1) into the system. y = x (–1) (–1) – 1 –1  y = –2 x – 3 ( – 1) –2 ( – 1) –3 – 1 2 – 3 – 1 – 1 

7. Sometimes it is difficult to tell exactly where the lines cross when you solve by graphing. It is good to confirm your answer by substituting it into both equations. Helpful Hint

8. Solve the system by graphing. Check your answer. Example 1 y = –2 x – 1 y = x + 5 Graph the system. The solution appears to be (–2, 3). Check Substitute (–2, 3) into the system. (–2, 3) is the solution of the system. y = x + 5 3 – 2 + 5 3 3  y = –2 x – 1 3 –2 ( – 2) – 1 3 4 – 1 3 3  y = x + 5 y = –2 x – 1