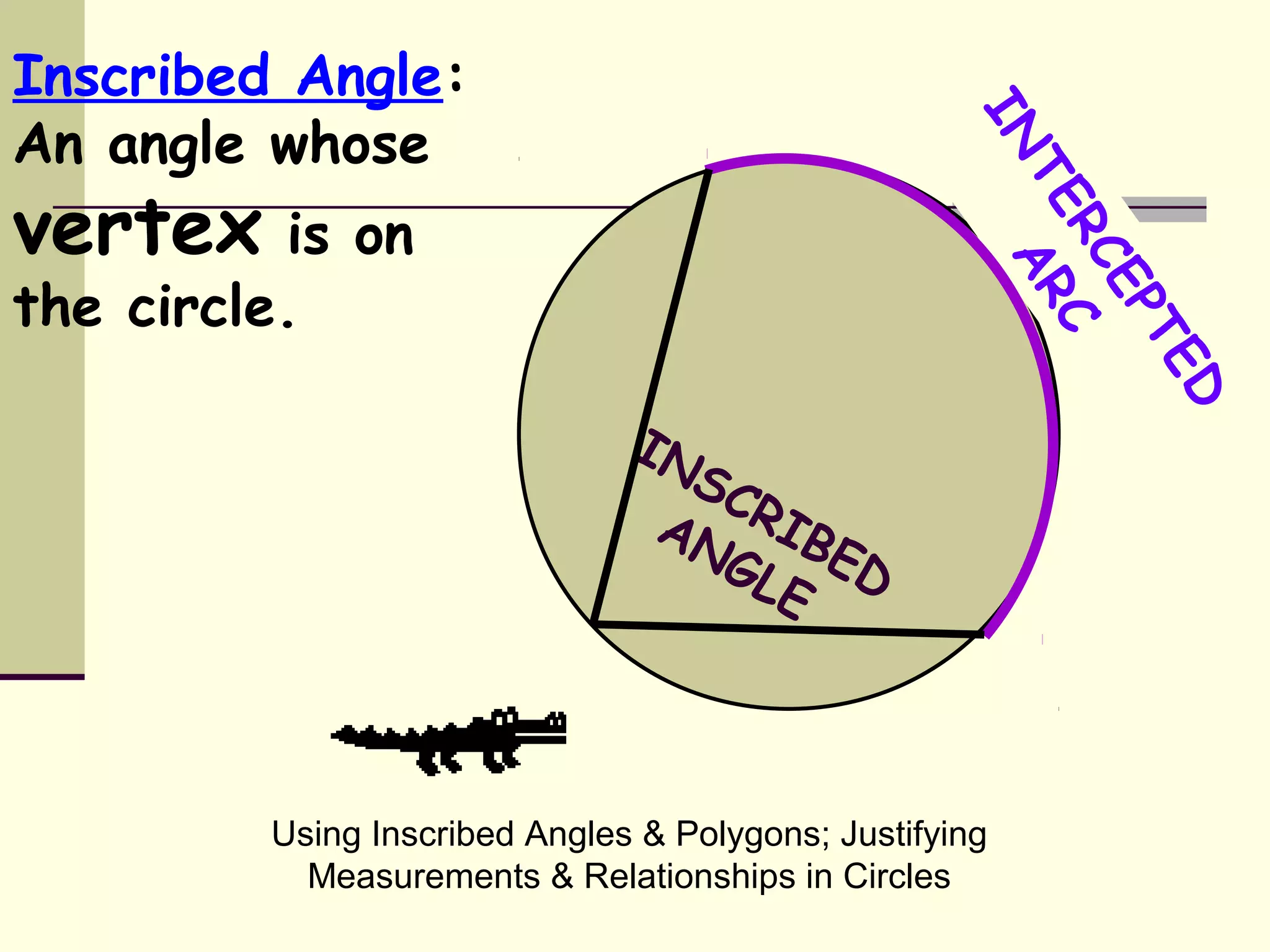
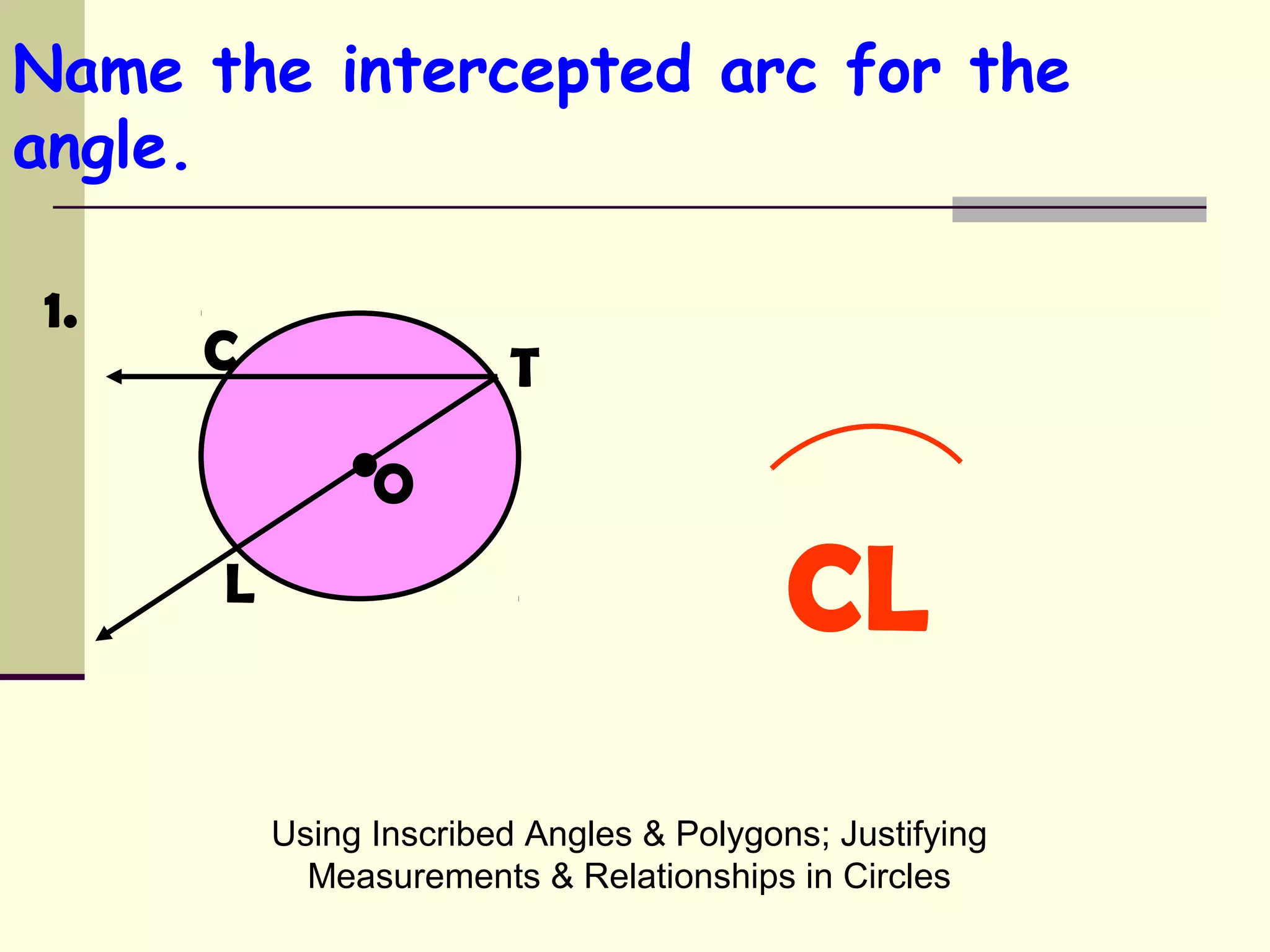
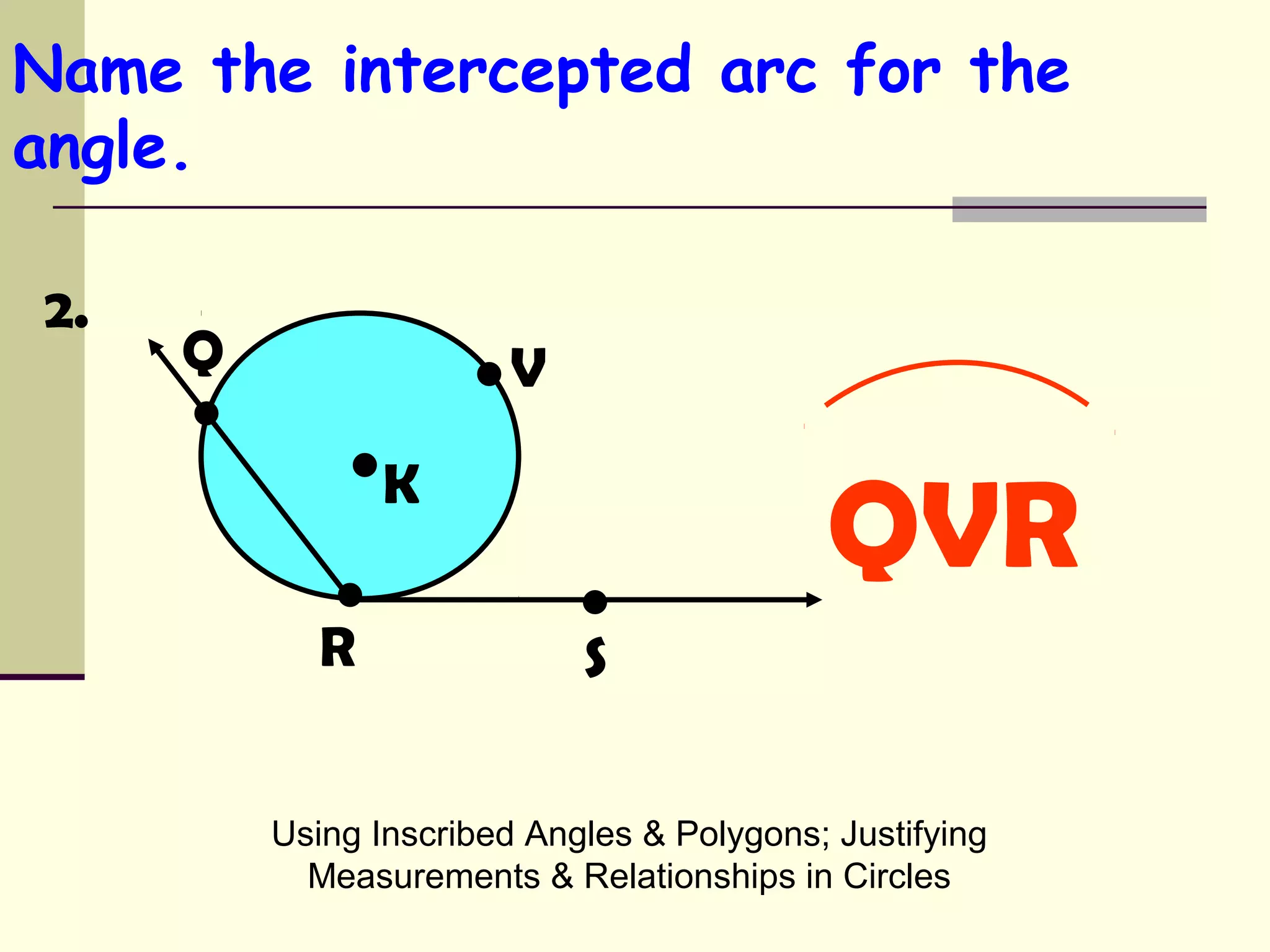
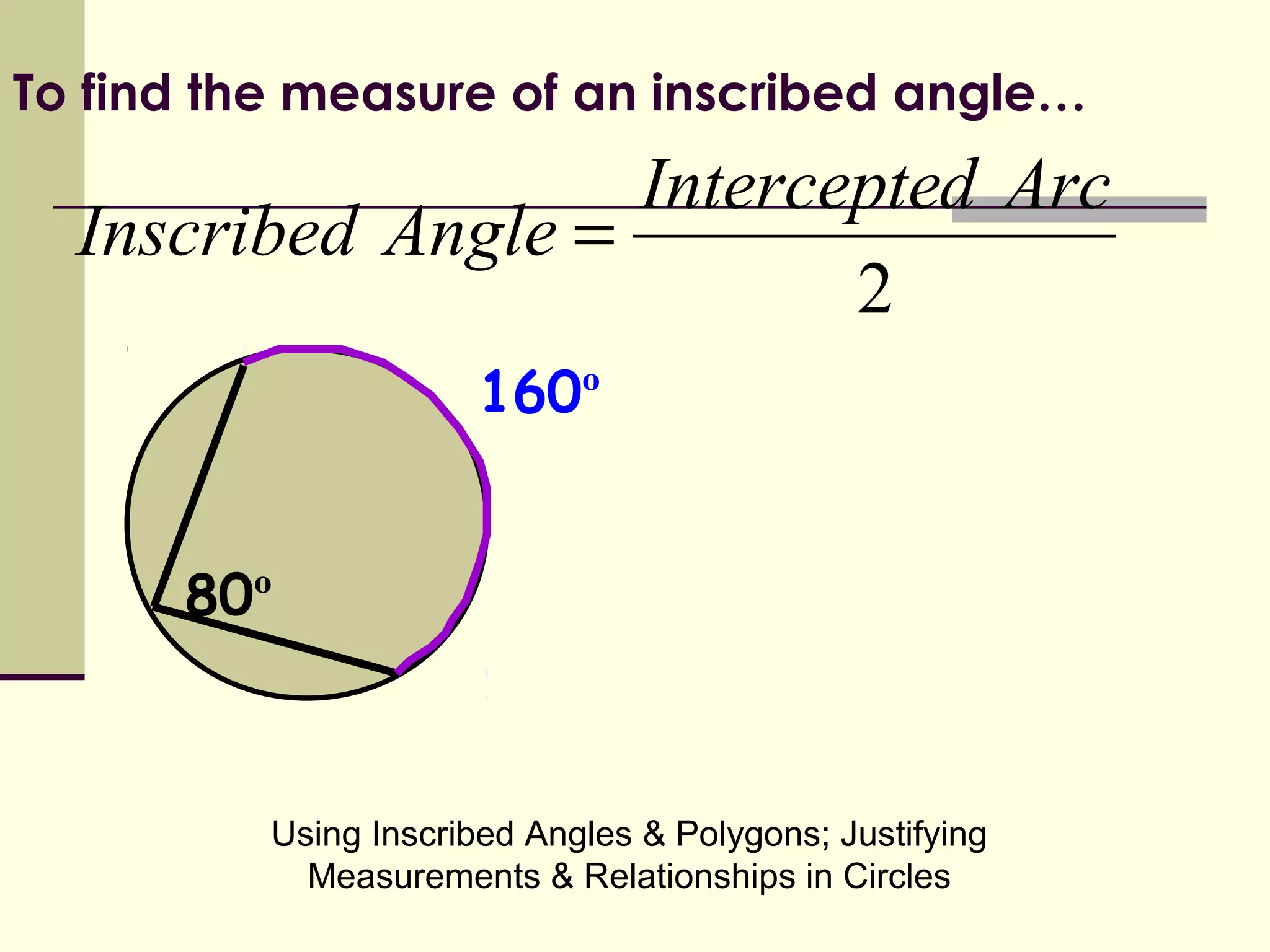
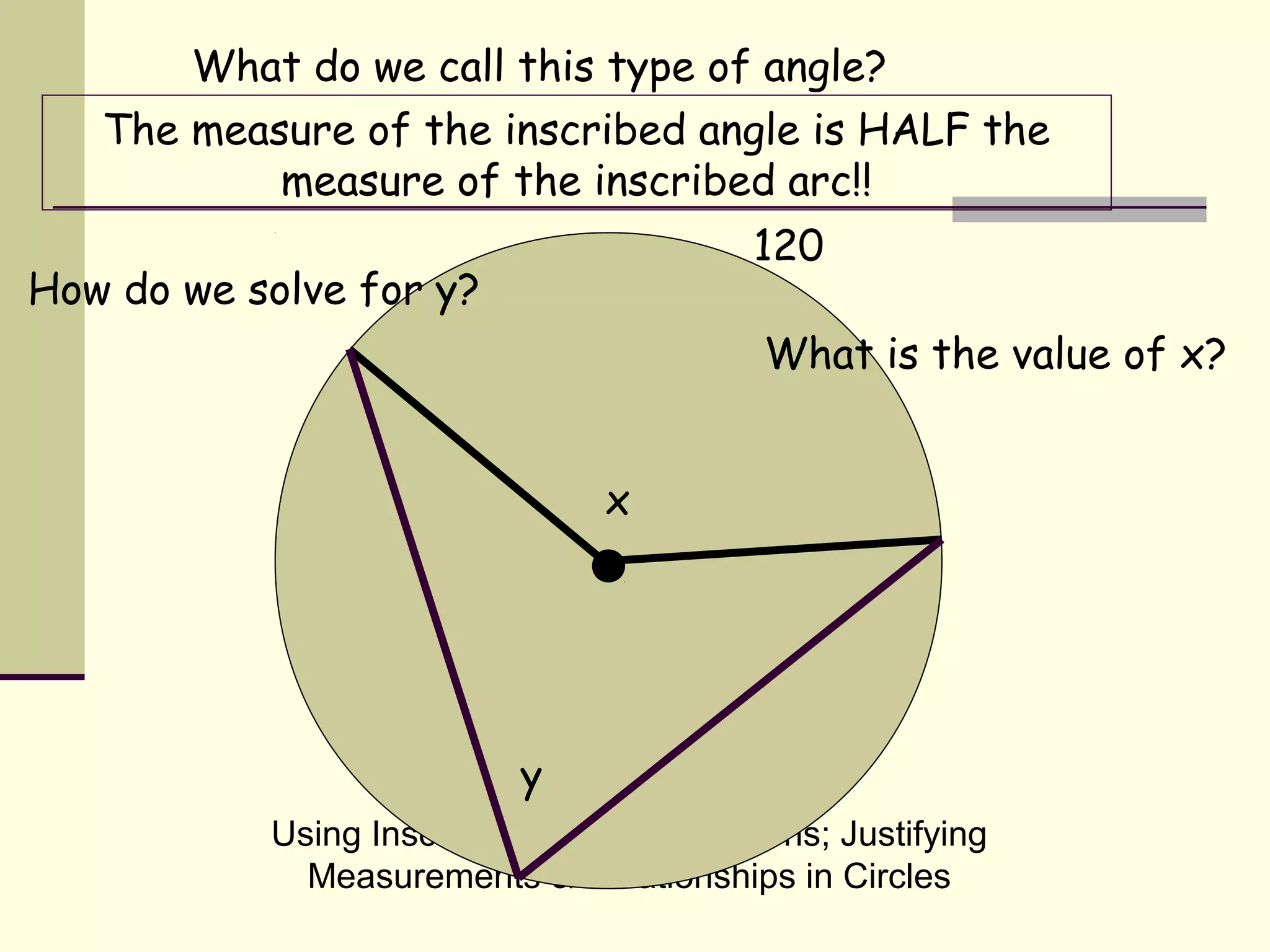
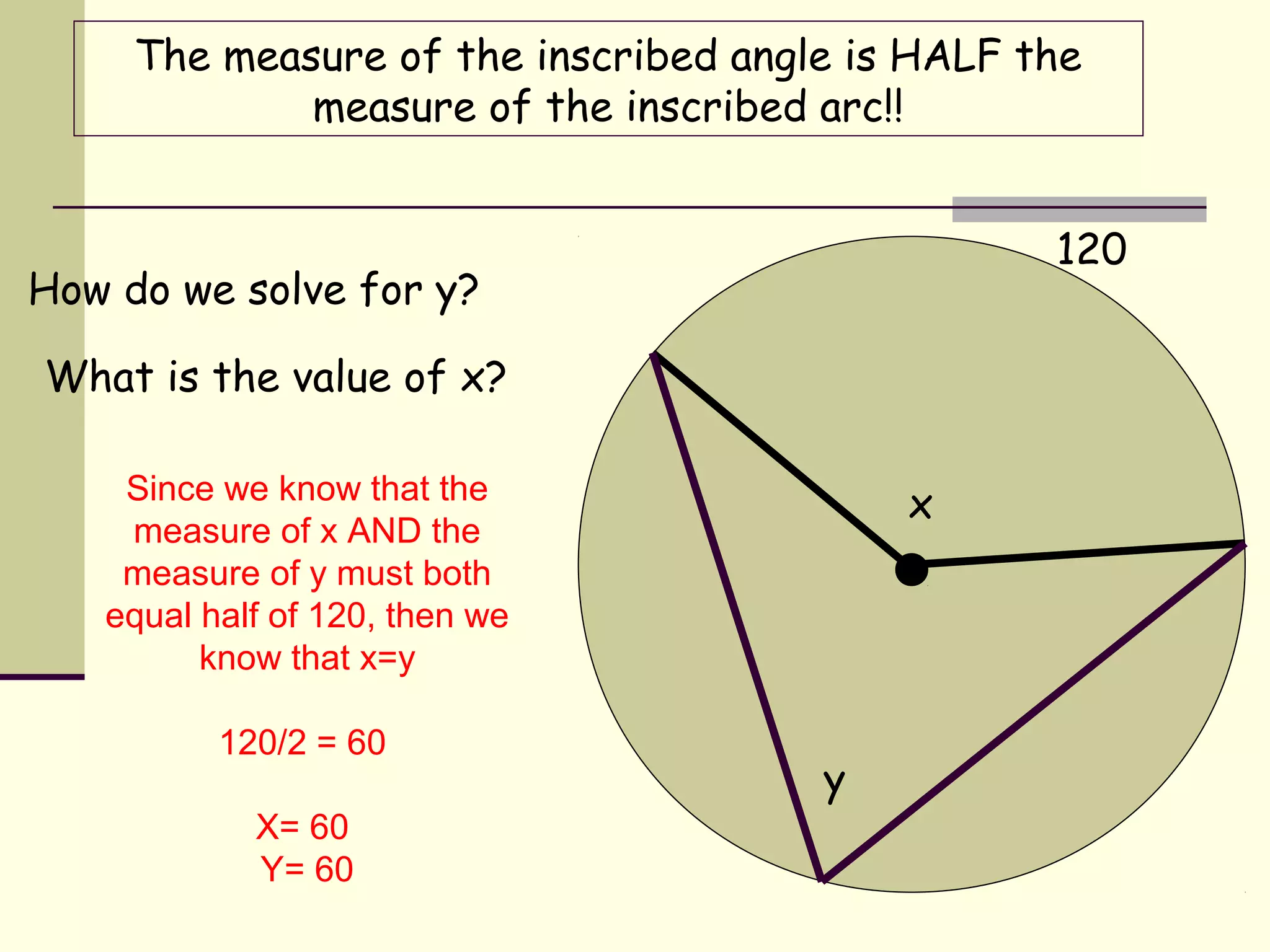
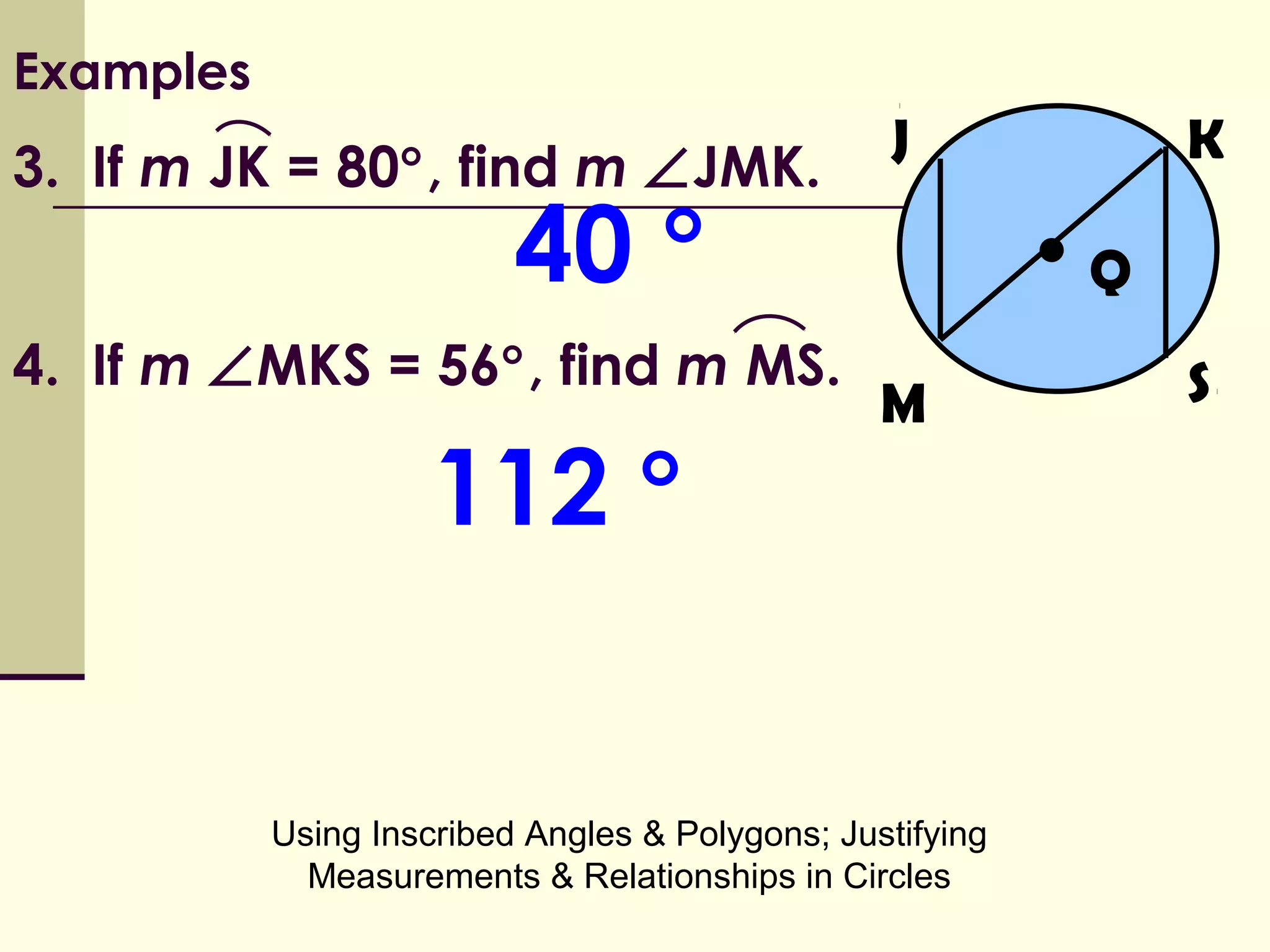
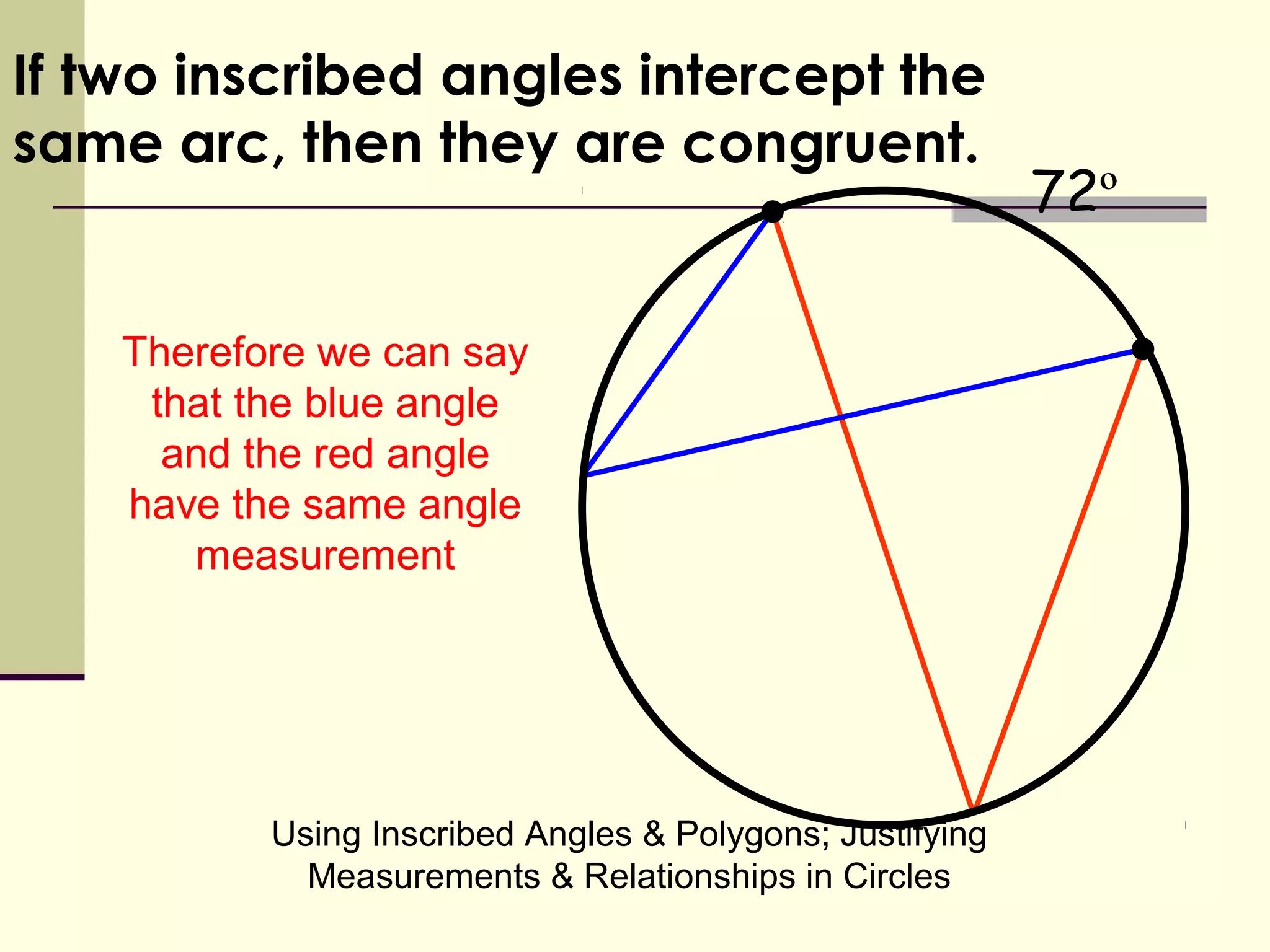
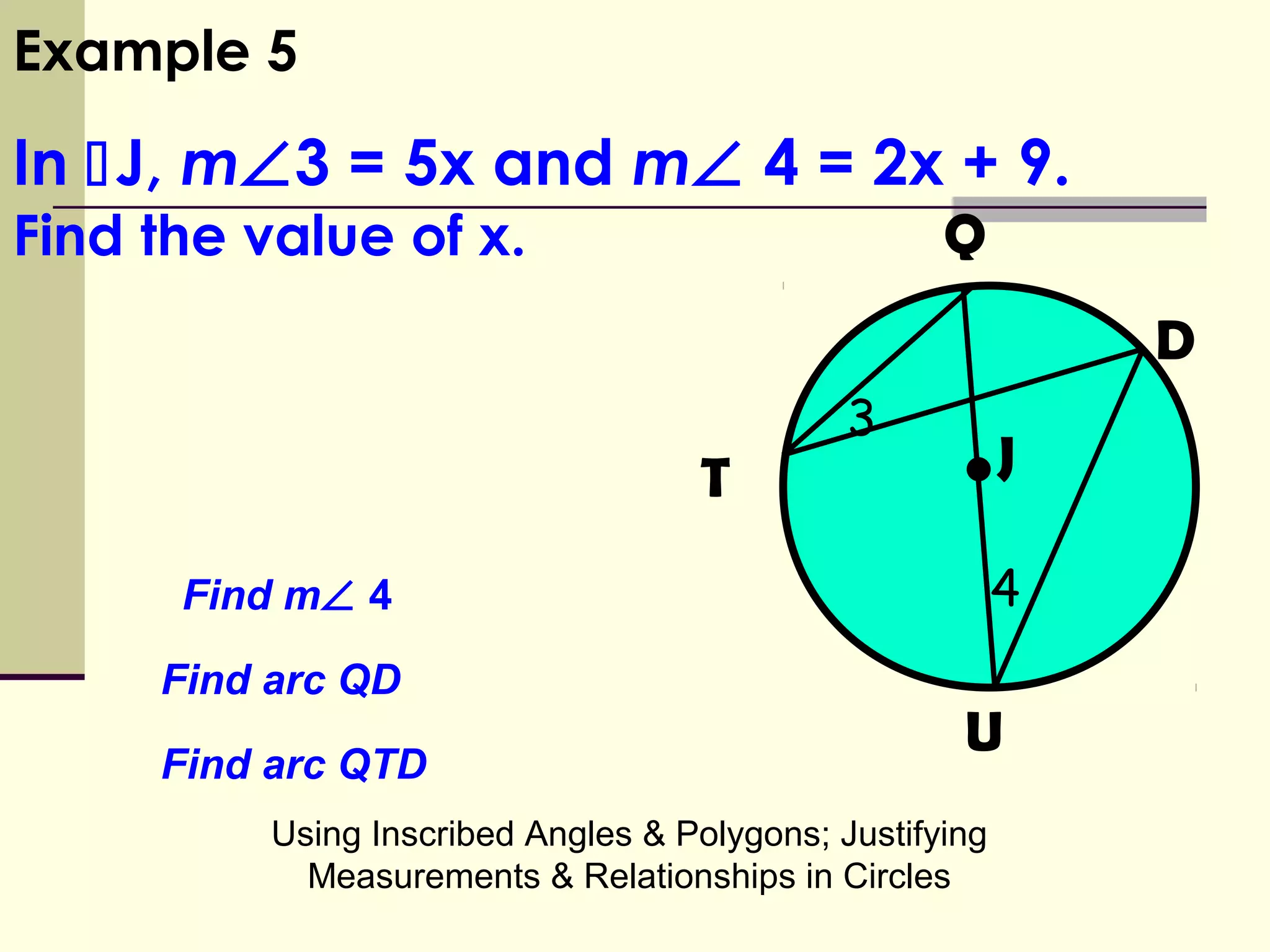
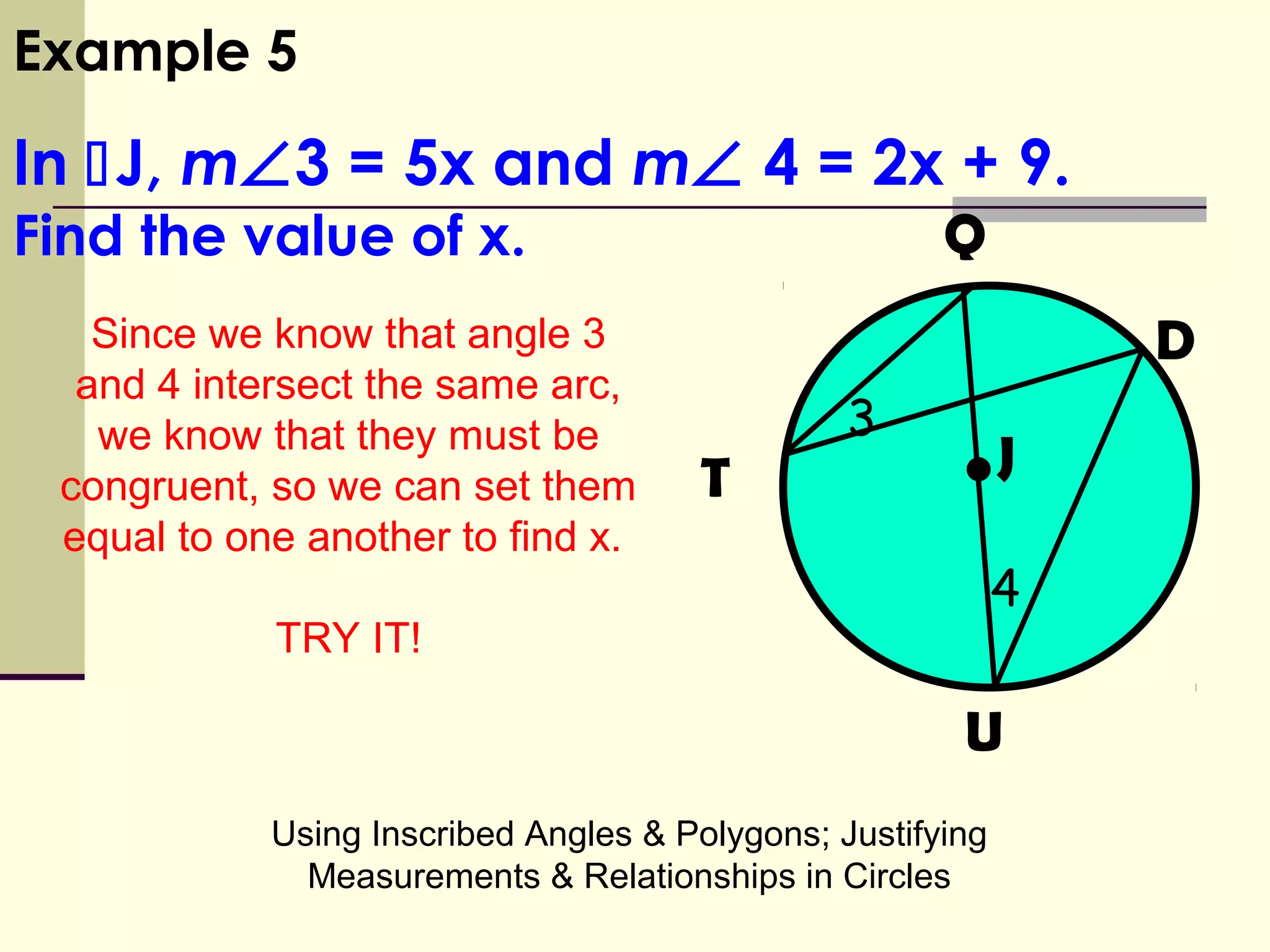
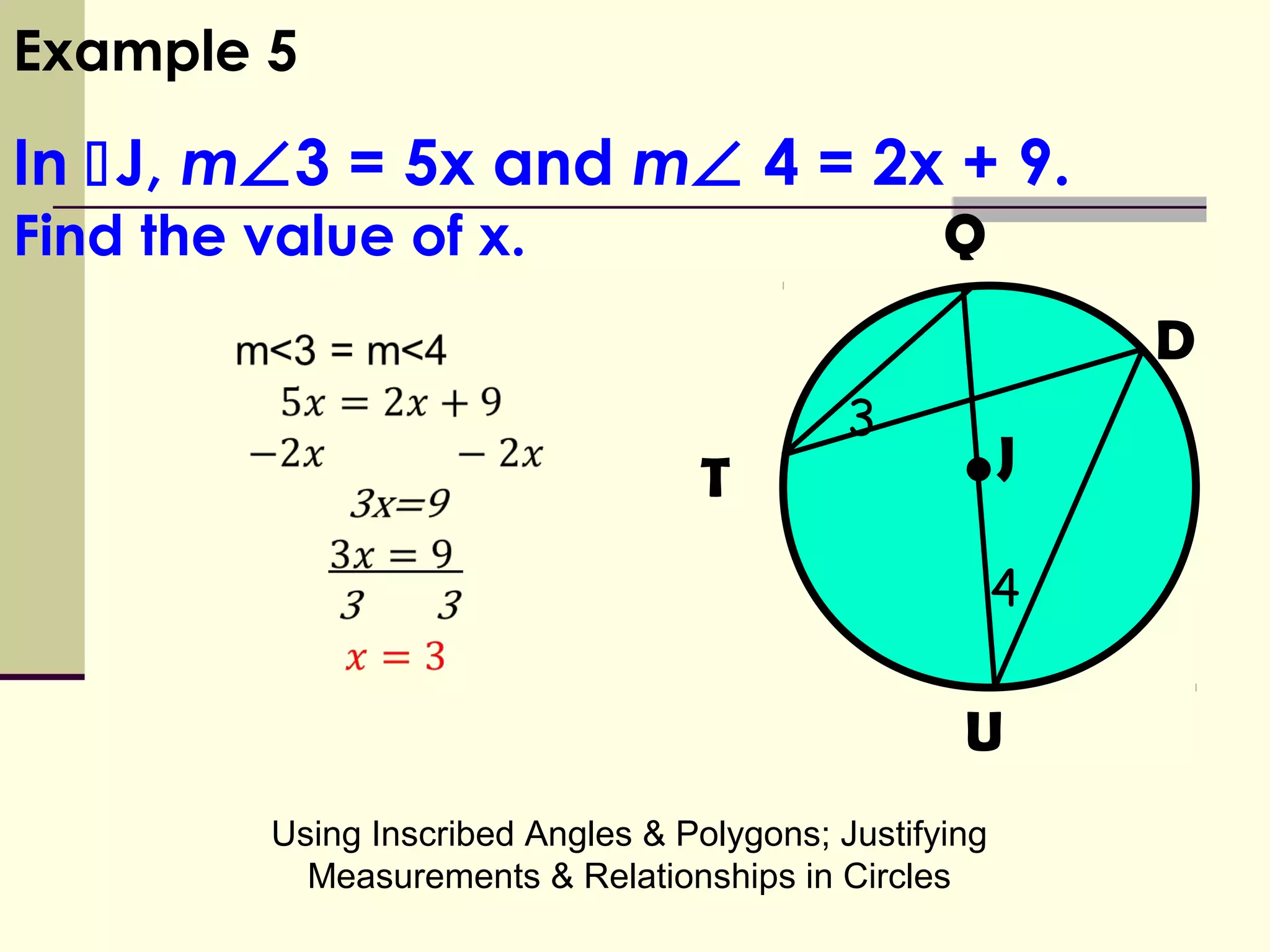
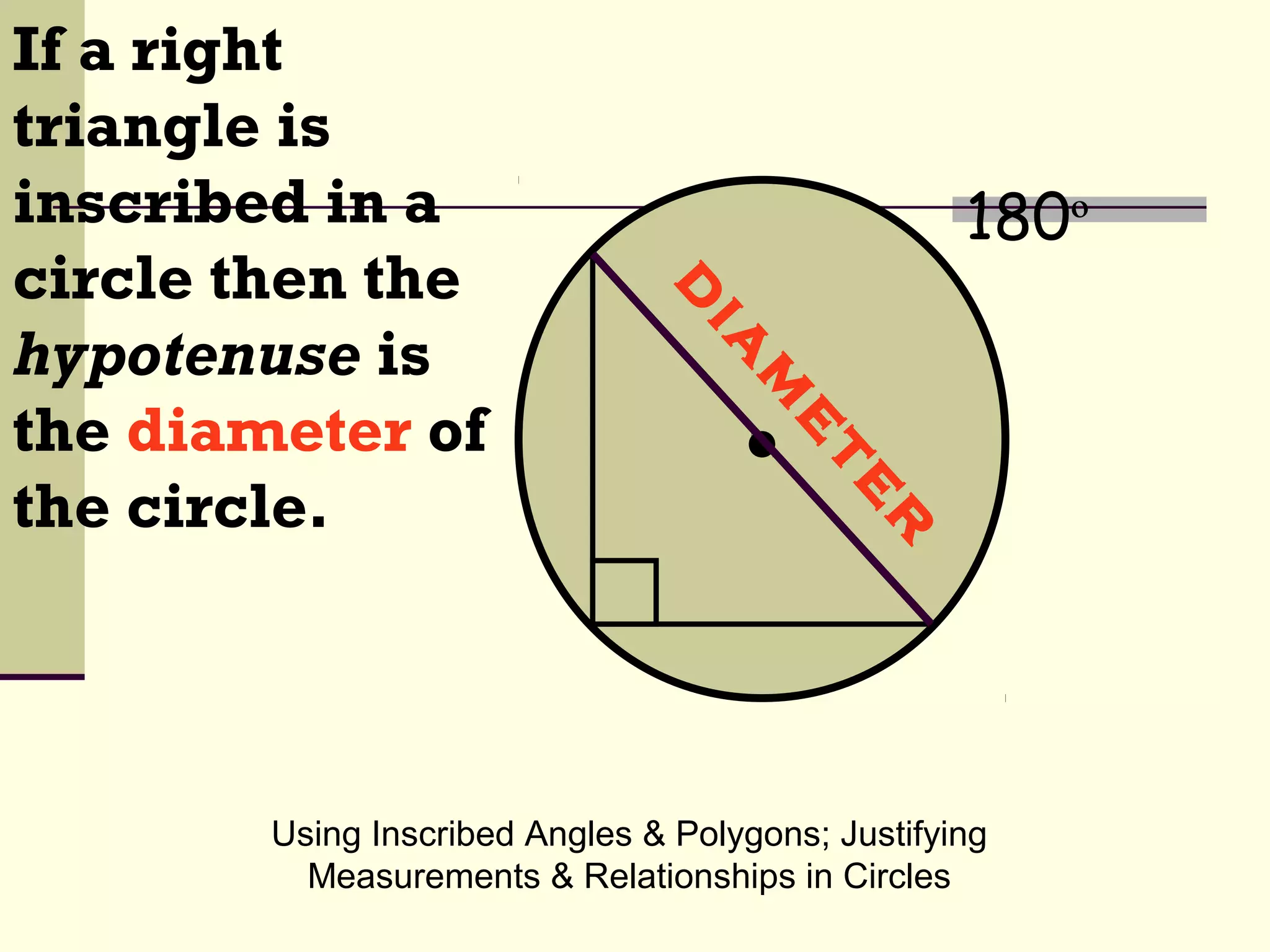
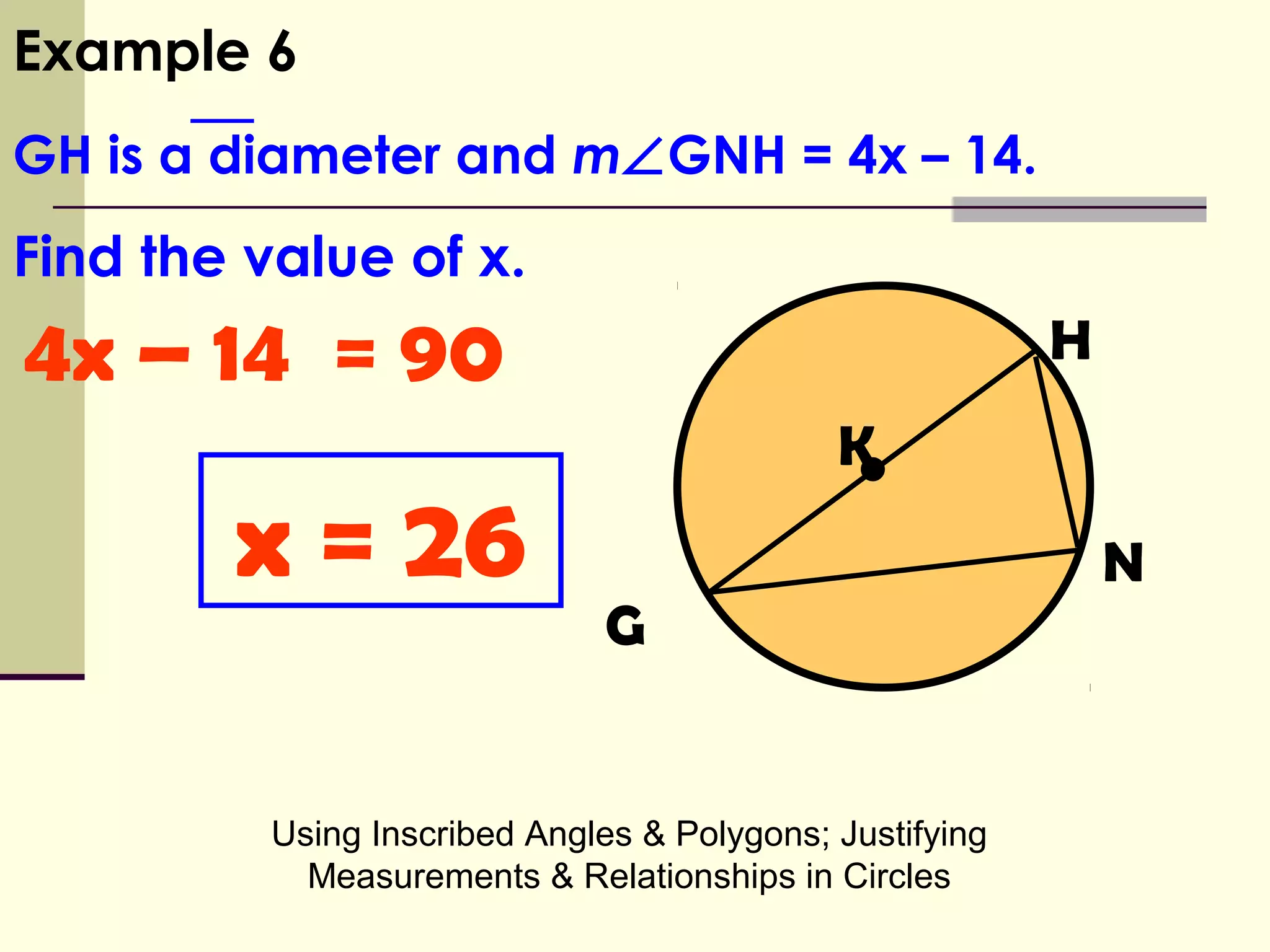
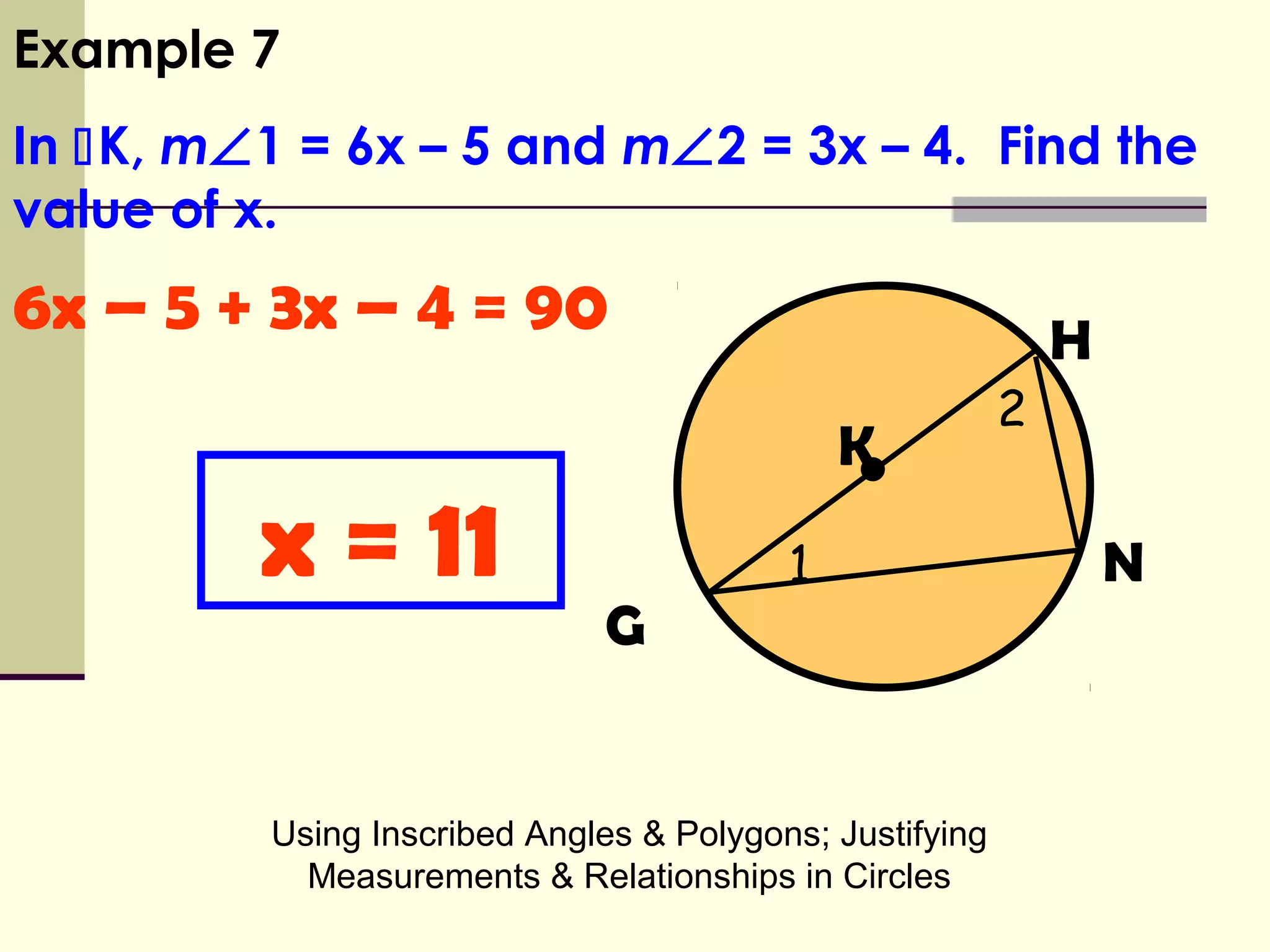
This document discusses inscribed angles and relationships in circles. It defines an inscribed angle as an angle whose vertex is on the circle. The measure of an inscribed angle is equal to half the measure of its intercepted arc. Examples are provided to demonstrate finding the measure of inscribed angles given arc measures, and vice versa. The document also states that if two inscribed angles intercept the same arc, they are congruent. It provides examples of solving for variables using the relationship between inscribed angles and their intercepted arcs.

1. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
14-1Inscribed Angles

2. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
Inscribed Angle:
An angle whose
vertex is on
the circle.
INSCRIBED
ANGLE
INTERCEPTED
ARC

3. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
Name the intercepted arc for the
angle.
•
C
L
O
T
1.
CL

4. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
Name the intercepted arc for the
angle.
•
Q
R
K
V
2.
QVR
S
•
•
•
•

5. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
2
ArcdIntercepte
AngleInscribed =
160º
80º
To find the measure of an inscribed angle…

6. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
120
x
What do we call this type of angle?
What is the value of x?
y
How do we solve for y?
The measure of the inscribed angle is HALF the
measure of the inscribed arc!!

7. 120
x
What is the value of x?
y
How do we solve for y?
The measure of the inscribed angle is HALF the
measure of the inscribed arc!!
Since we know that the
measure of x AND the
measure of y must both
equal half of 120, then we
know that x=y
120/2 = 60
X= 60
Y= 60

8. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
Examples
3. If m JK = 80°, find m ∠JMK.
•
M
Q
K
S
J
4. If m ∠MKS = 56°, find m MS.
40 °
112 °

9. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
72º
If two inscribed angles intercept the
same arc, then they are congruent.
Therefore we can say
that the blue angle
and the red angle
have the same angle
measurement

10. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
Example 5
In J, m∠3 = 5x and m∠ 4 = 2x + 9.
Find the value of x.
3
•
Q
D
JT
U
4Find m∠ 4
Find arc QD
Find arc QTD

11. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
Example 5
In J, m∠3 = 5x and m∠ 4 = 2x + 9.
Find the value of x.
3
•
Q
D
JT
U
4
Since we know that angle 3
and 4 intersect the same arc,
we know that they must be
congruent, so we can set them
equal to one another to find x.
TRY IT!

12. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
Example 5
In J, m∠3 = 5x and m∠ 4 = 2x + 9.
Find the value of x.
3
•
Q
D
JT
U
4

13. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
180º
d
ia
m
eter
If a right
triangle is
inscribed in a
circle then the
hypotenuse is
the diameter of
the circle.

14. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
•
H
K
G
N
4x – 14 = 90
Example 6
GH is a diameter and m∠GNH = 4x – 14.
Find the value of x.
x = 26

15. Using Inscribed Angles & Polygons; Justifying
Measurements & Relationships in Circles
•
H
K
G
N
6x – 5 + 3x – 4 = 90
Example 7
In K, m∠1 = 6x – 5 and m∠2 = 3x – 4. Find the
value of x.
x = 11 1
2